Probabilistic Forecasting in Decision-Making: New Methods and Applications
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

ADL Report to Global Forum on Cyberhate 2015
Report of the Anti-Defamation League on Confronting Cyberhate 5th Global Forum for Combating Anti-Semitism May, 2015 ANTI-DEFAMATION LEAGUE Barry Curtiss-Lusher National Chair Abraham H. Foxman National Director Kenneth Jacobson Deputy National Director Milton S. Schneider President, Anti-Defamation League Foundation CIVIL RIGHTS DIVISION Christopher Wolf Chair Deborah M. Lauter Director Steven M. Freeman Associate Director Eva Vega-Olds Assistant Director Jonathan Vick Assistant Director, Cyberhate Response CENTER ON EXTREMISM Mitch Markow Chair Oren Segal Director Lauren Steinberg Terrorism Analyst For additional and updated resources please see: www.adl.org Copies of this publication are available in the Rita and Leo Greenland Library and Research Center. ©2015 Anti-Defamation League | Printed in the United States of America | All Rights Reserved Anti-Defamation League 605 Third Avenue, New York, NY 10158-3560 www.adl.org Table of Contents PREFACE .........................................................................................................................................................4 INTRODUCTION ..............................................................................................................................................5 CHARTING PROGRESS ....................................................................................................................................6 A NEW CHALLENGE: TERRORIST USE OF SOCIAL MEDIA ............................................................................11 RECOMMENDATIONS -

Seamless Interoperability and Data Portability in the Social Web for Facilitating an Open and Heterogeneous Online Social Network Federation
Seamless Interoperability and Data Portability in the Social Web for Facilitating an Open and Heterogeneous Online Social Network Federation vorgelegt von Dipl.-Inform. Sebastian Jürg Göndör geb. in Duisburg von der Fakultät IV – Elektrotechnik und Informatik der Technischen Universität Berlin zur Erlangung des akademischen Grades Doktor der Ingenieurwissenschaften - Dr.-Ing. - genehmigte Dissertation Promotionsausschuss: Vorsitzender: Prof. Dr. Thomas Magedanz Gutachter: Prof. Dr. Axel Küpper Gutachter: Prof. Dr. Ulrik Schroeder Gutachter: Prof. Dr. Maurizio Marchese Tag der wissenschaftlichen Aussprache: 6. Juni 2018 Berlin 2018 iii A Bill of Rights for Users of the Social Web Authored by Joseph Smarr, Marc Canter, Robert Scoble, and Michael Arrington1 September 4, 2007 Preamble: There are already many who support the ideas laid out in this Bill of Rights, but we are actively seeking to grow the roster of those publicly backing the principles and approaches it outlines. That said, this Bill of Rights is not a document “carved in stone” (or written on paper). It is a blog post, and it is intended to spur conversation and debate, which will naturally lead to tweaks of the language. So, let’s get the dialogue going and get as many of the major stakeholders on board as we can! A Bill of Rights for Users of the Social Web We publicly assert that all users of the social web are entitled to certain fundamental rights, specifically: Ownership of their own personal information, including: • their own profile data • the list of people they are connected to • the activity stream of content they create; • Control of whether and how such personal information is shared with others; and • Freedom to grant persistent access to their personal information to trusted external sites. -
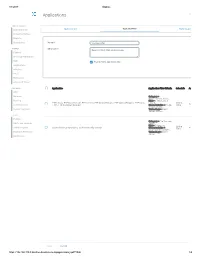
Applications Log Viewer
4/1/2017 Sophos Applications Log Viewer MONITOR & ANALYZE Control Center Application List Application Filter Traffic Shaping Default Current Activities Reports Diagnostics Name * Mike App Filter PROTECT Description Based on Block filter avoidance apps Firewall Intrusion Prevention Web Enable Micro App Discovery Applications Wireless Email Web Server Advanced Threat CONFIGURE Application Application Filter Criteria Schedule Action VPN Network Category = Infrastructure, Netw... Routing Risk = 1-Very Low, 2- FTPS-Data, FTP-DataTransfer, FTP-Control, FTP Delete Request, FTP Upload Request, FTP Base, Low, 4... All the Allow Authentication FTPS, FTP Download Request Characteristics = Prone Time to misuse, Tra... System Services Technology = Client Server, Netwo... SYSTEM Profiles Category = File Transfer, Hosts and Services Confe... Risk = 3-Medium Administration All the TeamViewer Conferencing, TeamViewer FileTransfer Characteristics = Time Allow Excessive Bandwidth,... Backup & Firmware Technology = Client Server Certificates Save Cancel https://192.168.110.3:4444/webconsole/webpages/index.jsp#71826 1/4 4/1/2017 Sophos Application Application Filter Criteria Schedule Action Applications Log Viewer Facebook Applications, Docstoc Website, Facebook Plugin, MySpace Website, MySpace.cn Website, Twitter Website, Facebook Website, Bebo Website, Classmates Website, LinkedIN Compose Webmail, Digg Web Login, Flickr Website, Flickr Web Upload, Friendfeed Web Login, MONITOR & ANALYZE Hootsuite Web Login, Friendster Web Login, Hi5 Website, Facebook Video -

Auswertung Onlinebefragung Social Media
HSD Auswertung Onlinebefragung Social Media Impressum Herausgeber Dezernat Kommunikation & Marketing Redaktion Rebecca Juwick M.A. Dezernat Kommunikation & Marketing Stand Februar 2016 2 Inhalt 1 Einleitung 4 2 Methode 5 3 Ergebnisse 6 Nutzung Social Networks 9 Zielgruppen 15 Funktionen & Inhalte 16 4 Fazit 22 3 Auswertung Social- Media-Umfrage 1 Einleitung Im Rahmen der Social-Media-Projektgruppe sollten die Anforderungen der unterschiedlichen Ziel- gruppen an das Social-Media-Angebot der Hochschule erhoben werden. Um dies möglichst effektiv umsetzen zu können, wurde eine Onlinebefragung für Studierende und Beschäftigte der Hochschule Düsseldorf durchgeführt. Diese liefen in zeitlichem Abstand zueinander jeweils 4 Wochen lang. Im Folgenden wird zuerst das methodische Vorgehen zur Befragung kurz erläutert, bevor die Ergeb- nisse vorgestellt werden. Alle Ergebnisse können den Datei-Anhängen „Auswertung_Studie- rende.xlsx“ und „Auswertung_Beschäftigte.xlsx“ entnommen werden. 4 Auswertung Social-Media-Umfrage 2 Methode Damit möglichst viele Studierende aus allen Fachbereichen und die Beschäftigten der Hochschule, unabhängig vom Standort, an der Erhebung teilnehmen konnten, wurde die Befragung als reine On- linebefragung durchgeführt. Aufgrund der Ähnlichkeit in Bezug auf die avisierten Zielgruppen, sowie der inhaltlichen Fragestellung wurde die Befragung in Kooperation mit der Campus IT, dem Daten- schutzbeauftragten und dem Fachbereich Sozial- und Kulturwissenschaften realisiert. Der Fragebogen wurde mithilfe der Software Unipark umgesetzt und über den entsprechenden Uni- park-Server für mehrere Wochen zur Beantwortung verfügbar gehalten. Der Umfang des Fragebo- gens wurde dabei so gewählt, dass eine Bearbeitungsdauer von 10 bis 15 Minuten – inklusive Brie- fing und Debriefing – nicht überschritten wurde. Zur Gewinnung von Teilnehmenden wurden diese über diverse Kanäle angesprochen. Auf der Start- seite des Internetauftritts der HSD wurde beispielsweise eine Meldung von der Pressestelle einge- stellt. -

The National Hillumat Otti
THE NATIONALUS009742853B2 HILLUMAT OTTI TIK (12 ) United States Patent ( 10 ) Patent No. : US 9 , 742 ,853 B2 Auerbach (45 ) Date of Patent: Aug. 22 , 2017 ( 54 ) DYNAMIC COMPUTER SYSTEMS AND ( 56 ) References Cited USES THEREOF U . S . PATENT DOCUMENTS (71 ) Applicant : Michael H . Auerbach , Rockville , MD 6 ,850 , 511 B2 2 /2005 Kats et al. (US ) 7 ,002 , 944 B2 2 /2006 Kats et al. (72 ) Inventor : Michael H . Auerbach, Rockville , MD (Continued ) (US ) FOREIGN PATENT DOCUMENTS ( 73 ) Assignee : The Michael Harrison Tretter EP 2151793 2 /2010 Auerbach Trust , New York , NY (US ) WO WO 2010 / 144766 12 / 2010 ( * ) Notice : Subject to any disclaimer, the term of this (Continued ) patent is extended or adjusted under 35 U . S . C . 154 (b ) by 177 days . OTHER PUBLICATIONS Ahtiainen , A . et al. (2009 ) “ Awareness Networking in Wireless (21 ) Appl. No. : 14 /512 ,442 Environments ,” Vehicular Technol. Mag . IEEE 4 ( 3 ) : 48 , 54 . ( 22 ) Filed : Oct. 12 , 2014 (Continued ) Pri Primary Examiner - Kevin Bates (65 ) Prior Publication Data Assistant Examiner — Nazia Naoreen US 2015 /0334044 A1 Nov . 19, 2015 ( 74 ) Attorney , Agent, or Firm — Jeffrey I. Auerbach ; AuerbachSchrot LLC Related U . S . Application Data (60 ) Provisional application No. 62/ 000 ,015 , filed on May (57 ) ABSTRACT 19 , 2014 . The invention concerns computer systems that are specially adapted to propagate content over a dynamic network , (51 ) Int. Cl. substantially in real time, by virtue of the locational prox H04L 12 /911 (2013 . 01) imity of network joined client computers . Preferably, the G06F 1730 ( 2006 .01 ) content will also be proximity -weighted , and more prefer ably also rank -weighted , topic -weighted , time -weighted , (Continued ) query - weighted , vote -weighted , and / or location - weighted . -

NAS 232 Using Aifoto on Your Mobile Devices
NAS 232 Using AiFoto on Your Mobile Devices Manage photos on your NAS using your mobile device ASUSTOR COLLEGE NAS 232: Using AiFoto on Your Mobile Devices Devices COURSE OBJECTIVES Upon completion of this course you should be able to: 1. Use AiFoto to manage photos and albums on your NAS and mobile device. PREREQUISITES Course Prerequisites: NAS 137: Introduction to Photo Gallery Students are expected to have a working knowledge of: N/A OUTLINE 1. Introduction to AiFoto 1.1 Introduction to AiFoto 2. Basic Functions 2.1 Settings and instructions 2.2 Connecting to your NAS with AiFoto 2.3 Browsing photos with AiFoto 3. Managing albums and photos 3.1 Album management 3.1.1 Creating albums 3.1.2 Editing album information 3.1.3 Deleting albums 3.1.4 Uploading and downloading albums 3.2 Photo management ASUSTOR COLLEGE / 2 NAS 232: Using AiFoto on Your Mobile Devices Devices 3.3 Using Camera Mode 3.4 Uploading your local camera roll to your NAS 3.5 Privacy settings 4. Notes ASUSTOR COLLEGE / 3 NAS 232: Using AiFoto on Your Mobile Devices Devices 1. Introduction to AiFoto 1.1 Introduction to AiFoto AiFoto lets you access Photo Gallery from your ASUSTOR NAS on your mobile device! With AiFoto you can user your mobile device to browse and manage your NAS web photo albums and instantly upload photos from your mobile device camera roll to your NAS. AiFoto also provides you with a Camera Mode allowing you to specify an album and then have any photos you take automatically uploaded to the album. -

Systematic Scoping Review on Social Media Monitoring Methods and Interventions Relating to Vaccine Hesitancy
TECHNICAL REPORT Systematic scoping review on social media monitoring methods and interventions relating to vaccine hesitancy www.ecdc.europa.eu ECDC TECHNICAL REPORT Systematic scoping review on social media monitoring methods and interventions relating to vaccine hesitancy This report was commissioned by the European Centre for Disease Prevention and Control (ECDC) and coordinated by Kate Olsson with the support of Judit Takács. The scoping review was performed by researchers from the Vaccine Confidence Project, at the London School of Hygiene & Tropical Medicine (contract number ECD8894). Authors: Emilie Karafillakis, Clarissa Simas, Sam Martin, Sara Dada, Heidi Larson. Acknowledgements ECDC would like to acknowledge contributions to the project from the expert reviewers: Dan Arthus, University College London; Maged N Kamel Boulos, University of the Highlands and Islands, Sandra Alexiu, GP Association Bucharest and Franklin Apfel and Sabrina Cecconi, World Health Communication Associates. ECDC would also like to acknowledge ECDC colleagues who reviewed and contributed to the document: John Kinsman, Andrea Würz and Marybelle Stryk. Suggested citation: European Centre for Disease Prevention and Control. Systematic scoping review on social media monitoring methods and interventions relating to vaccine hesitancy. Stockholm: ECDC; 2020. Stockholm, February 2020 ISBN 978-92-9498-452-4 doi: 10.2900/260624 Catalogue number TQ-04-20-076-EN-N © European Centre for Disease Prevention and Control, 2020 Reproduction is authorised, provided the -

Social Media and the ISIS Narrative Daniel Cunningham, MA Sean F
Social Media and the ISIS Narrative Daniel Cunningham, MA Sean F. Everton, PhD Robert Schroeder, MA Department of Defense Analysis Naval Postgraduate School Monterey, CA 93943 March 20, 2015 Abstract The Islamic State of Iraq and Syria (ISIS) has attracted the world’s attention and much of its wrath, primarily because of its rapid expansion in Iraq and Syria, its brutal treatment of religious minorities (e.g., Yazidis, Christians), and its beheadings of hostages from Western countries. At this point, it is unclear whether the group represents a global or a sectarian form of jihadism. Is it similar to al-Qaeda, which seeks to target the far enemy (i.e., Western countries such as the U.S. that some in the Muslim world believe exert a corrupting influence on Islamic countries), or is it more sectarian in that it focuses on targeting what it perceives to be the near enemies of Islam (i.e., “corrupt” Islamic nations)? In this paper we address this debate by examining ISIS’s online presence on the social media platform, Twitter, which serves as a forum for supporters to post and receive messages, images, videos, and links to websites to and from a wide-audience. The speed at which users can transmit and receive information via Twitter suggests that an analysis of ISIS-related user accounts and the key themes and concepts they disseminate can contribute to a better understanding of the group’s overall narrative. We examine ISIS’s online presence by extracting from Twitter the semantic networks of its most influential users. We find that a shift may be occurring in the ISIS narrative, from one that focuses on the near enemy to one that focuses on the far enemy. -

NAS 137 Introduction to Photo Gallery
NAS 137 Introduction to Photo Gallery Manage and share the photos on your ASUSTOR NAS ASUSTOR COLLEGE NAS 137: Introduction to Photo Gallery COURSE OBJECTIVES Upon completion of this course you should be able to: 1. Use Photo Gallery to manage and share the photos on your ASUSTOR NAS. PREREQUISITES Course Prerequisites: None Students are expected to have a working knowledge of: N/A OUTLINE 1. Introduction to Photo Gallery 1.1 Introduction to Photo Gallery 1.2 Where to get Photo Gallery 2. Using Photo Gallery 2.1 Installing Photo Gallery 2.2 Creating a new album 2.3 Album and Photo Management 2.3.1 Album management 2.3.2 Photo management 2.3.3 Search 2.3.4 Viewing photos individually and via slideshow 2.4 Co-managing albums 2.5 Social media sharing 3. Notes ASUSTOR COLLEGE / 2 NAS 137: Introduction to Photo Gallery 1. Introduction to Photo Gallery 1.1 Introduction to Photo Gallery Photo Gallery is a dedicated web photo album application for ASUSTOR NAS. After downloading and installing Photo Gallery from App Central, NAS administrators will be able to browse their photo collection on the NAS from any PC along with co-managing and sharing albums with NAS users. Photo Gallery utilizes a modern cover design for albums which is comprised of a large photo with 4 smaller thumbnails of recently uploaded photos. This allows users to easily organize their photos and keep track of the latest changes by simply viewing the album cover. Photo Gallery features a clear and crisp interface with an easy to browse photo wall along with a built-in thumbnail accelerator that allows users to quickly browse all photos. -

Sept Thèses Sur La Fediverse Et Le Devenir Du Logiciel Libre Par Aymeric Mansoux Et Roel Roscam Abbing
Sept Thèses sur la Fediverse et le devenir du logiciel libre par Aymeric Mansoux et Roel Roscam Abbing Framalang met à votre disposition la traduction de l’ouvrage en anglais Seven Theses on the Fediverse and the becoming of FLOSS Licence Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International. Traduction Framalang : Claire, dodosan, goofy, jums, Macrico, Mannik, mo, roptat, tykayn, wisi_eu À la rencontre de la Fédiverse Ces dernières années, dans un contexte de critiques constantes et de lassitude généralisée associées aux plates-formes de médias sociaux commerciaux 1, le désir de construire des alternatives s’est renforcé. Cela s’est traduit par une grande variété de projets animés par divers objectifs. Les projets en question ont mis en avant leurs différences avec les médias sociaux des grandes plates-formes, que ce soit par leur éthique, leur structure, les technologies qui les sous-tendent, leurs fonctionnalités, l’accès au code source ou encore les communautés construites autour d’intérêts spécifiques qu’ils cherchent à soutenir. Bien que diverses, ces plates-formes tendent vers un objectif commun : remettre clairement en question l’asservissement à une plate-forme unique dans le paysage des médias sociaux dominants. Par conséquent, ces projets nécessitent différents niveaux de décentralisation et d’interopérabilité en termes d’architecture des réseaux et de circulation de données. Ces plates-formes sont regroupées sous le terme de « Fédiverse », un mot-valise composé de « Fédération » et « univers ». La fédération est un concept qui vient de la théorie politique par lequel divers acteurs qui se constituent en réseau décident de coopérer tous ensemble. -

Twittering* for Work and Health
Twitter Twittering* for Work & Health • http://twitter.com/ * (and Plurking) PF Anderson, Emerging Technologies Librarian, Health Sciences Libraries, University of Michigan, [email protected] July 15, 2008 Twitter lifecycle Twitter is … • Twitter is a type of tool • Twitter = Microblogging (sort of) • Microblogging ≠ Twitter • Microblogging = (Twitter OR Jaiku OR Pownce OR Plurk OR Tumblr) • http://cogdoghouse.wikispaces.com/TwitterCycle Twitter is … • for friends • for news • for current events • for crisis response • for silliness • for intelligent discussion Twitter for • like fishing • like sex productivity • like a chatroom • a microblogging tool • an RSS feed generator • • the social search engine • and what else? we’ve all been waiting for 1 Twitter + time management Twitter + task management Twitter + calendar Twitter + weather Twitter + traffic More 2 Twitter + health news Twitter for discovery Twitter + health Twitter + health news news Today’s buzz – Google Health Twitter + health legislation • HR 2790 – Physician Assistants 3 Today’s buzz – Google Health Today’s buzz - Google Health • attillacsordas Today’s buzz - Google Health Today’s buzz - Google Health • dporter • laktek Today’s buzz - Google Health Today’s buzz - Google Health • Google • Google API 4 Twitter + science Using Twitter in health & healthcare Twitter + doctors Twitter + nurses Twitter + Telemedicine + Twitter + dentists Second Opinion 5 Twitter + activism Twitter + make a difference Twitter + exercise Twitter + health tracking • “Tweet your pain” Twitter + food -

La Fée Diverse Déploie Ses Ailes
La Fée diverse déploie ses ailes Il n’est pas si fréquent que l’équipe Framalang traduise un article depuis la langue italienne, mais la récapitulation bien documentée de Cagizero était une bonne occasion de faire le point sur l’expansion de la Fediverse, un phénomène dont nous nous réjouissons et que nous souhaitons voir gagner plus d’amplitude encore, tant mieux si l’article ci-dessous est très lacunaire dans un an ! Article original : Mastodon, il Fediverso ed il futuro decentrato delle reti sociali Traduction Framalang : alainmi, Ezelty, goofy, MO Mastodon, la Fediverse et l’avenir des réseaux décentralisés par Cagizero Peu de temps après une première vue d’ensemble de Mastodon il est déjà possible d’ajouter quelques observations nouvelles. Tout d’abord, il faut noter que plusieurs personnes familières de l’usage des principaux médias sociaux commerciaux (Facebook, Twitter, Instagram…) sont d’abord désorientées par les concepts de « décentralisation » et de « réseau fédéré ». En effet, l’idée des médias sociaux qui est répandue et bien ancrée dans les esprits est celle d’un lieu unique, indifférencié, monolithique, avec des règles et des mécanismes strictement identiques pour tous. Essentiellement, le fait même de pouvoir concevoir un univers d’instances séparées et indépendantes représente pour beaucoup de gens un changement de paradigme qui n’est pas immédiatement compréhensible. Dans un article précédent où était décrit le média social Mastodon, le concept d’instance fédérée était comparé à un réseau de clubs ou cercles privés associés entre eux. Certains aspects exposés dans l’article précédent demandent peut-être quelques éclaircissements supplémentaires pour celles et ceux qui abordent tout juste le concept de réseau fédéré.