DOCSLIB.ORG

Losses and Dispersion in Waveguides

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Losses and Dispersion in Waveguides Losses and Dispersion in Waveguides Wei-Chih WangInstitute of Nanoengineeirng and Microsystems National Tsing Hua University w.wang 1 • dB is a ratio of the power received verses the power transmitted Loss (dB) = 10log (power transmitted / power received) w.wang 2 Intrisic Loss Mechanism • Scattering Loss Predominated in glass or dielectric (such as oxide) waveguides. • Absorption Loss Most important in semiconductor and other crystalline materials. • Radiation Loss w.wang 3 Higher order mode Lower order mode w.wang 4 (loss coefficient) is the propagation constant in x direction = in substrate and cover tg is glass thickness w.wang 5 Scattering The scattering from molecules and very tiny particles (< 1 /10 wavelength) is predominantly Rayleigh scattering. For particle sizes larger than a wavelength, Mie scattering predominates. This scattering produces a pattern like an antenna lobe, with a sharper and more intense forward lobe for larger particles. HyperPhysics Mie scattering is not strongly wavelength dependent and produces the almost white glare around the sun when a lot of particulate material is present in the air. It also gives us the the white light from mist and fog. w.wang 6 Blue Sky HyperPhysics w.wang 7 Rayleigh Scattering (small particle scattering) The random localized variations of the molecular positions in glass create random inhomogeneities of the refractive index that acts as tiny scattering centers. The amplitude of the scattered field is proportional to 2. The intensity is therefore proportional to 4 or 1/4 Joseph C. Palais Rayleigh scattering occurs when the size of the density fluctuation (waveguide defect) is less than one-tenth of the w.wangoperating wavelength of light, fucntion of wavelength. See blue sky because shorter wavelength 8 Rayleigh Scattering HyperPhysics It is Rayleigh scattering off the molecules of the air which gives us the blue sky. w.wang 9 Absorption Coefficient Due to Rayleigh Scattering w.wang 10 Absorption Coefficient Due to Rayleigh Scattering Shorter the wavelength the more w.wang Rayleigh scattering 11 Mie scattering (larger particle scattering) If the size of the defect is greater than one-tenth of the wavelength of light, the scattering mechanism is called Mie scattering. Mie scattering, caused by these large defects in the fiber core, scatters light out of the fiber core. However, in commercial fibers, the effects of Mie scattering are insignificant. Optical fibers are manufactured with very few large defects. w.wang 12 • Light striking the Ge molecules in the core can be scattered into new pathways out of the fiber • Rayleigh Scattering accounts for 95% of fiber attenuation • Optical Time Domain Reflectometers (OTDR) use this property to measurew.wang loss in a fiber 13 Absorption Joseph C. Palais w.wang 14 Absorption Absorption is a major cause of signal loss in an optical fiber. Absorption is defined as the portion of attenuation resulting from the conversion of optical power into another energy form, such as heat. Absorption in optical fibers is explained by three factors: •Imperfections in the atomic structure of the fiber material •The intrinsic or basic fiber-material properties •The extrinsic (presence of impurities) fiber-material properties Imperfections in the atomic structure induce absorption by the presence of missing molecules or oxygen defects. Absorption is also induced by the diffusion of hydrogen molecules into the glass fiber. Since intrinsic and extrinsic material properties are the main cause of absorption w.wang w.wang 16 = w.wang 17 w.wang 18 Absorption in Silica based Optical Fiber Silica glass (SiO2) is strongly dependent on wavelength. The material has strong absorption around middle-infrared (due to vibrational transitions) and UV (due to electronic and molecular transitions) Absorption in optical fibers is explained by three factors: • Imperfections in the atomic structure of the fiber material - induce absorption by the presence of missing molecules or oxygen defects. • The intrinsic or basic fiber-material properties - UV (due to electronic and molecular transitions) - middle-infrared (due to vibrational transitions) • The extrinsic (presence of impurities) fiber-material properties - OH radicals - transition metal ions w.wang 19 Dependence of the attenuation coefficient of silica glass on wavelengths Scientific and Technological Education in Photonics Silica glass (SiO2) is strongly dependent on wavelength. w.wang 20 UV- electric transitions associated with bandgap in SiO2 IR – molecules vibrations (phonons) Fundamental Molecular vibration B-O 7.3 m P-O 8.0 m Si-O 9.0 m Ge-O 11.0 m w.wang 21 UV and IR Absorption Urbach Tail: GeO2 shifts to longer wavelength: 4.6/ uv = (1.59/(47g+60)) e g= mole function =0.02 (GeO2) small @1.3m wavelength in mm uv => dB/km .IR/ IR= A e Where A = 8x1011 dB/km .IR/= 48.5m w.wang 22 Assignment Calculation of losses using the dB scale become easy. For example, if we have a 40-km fiber link (with a loss of 0.4 dB/km) having 3 connectors in its path and if each connector has a loss of 1.8 dB, the total loss will be the sum of all the losses in dB; or 0.4 dB/km × 40 km + 3 × 1.8 dB = 21.4 dB. Let us assume that the input power of a 5-mW laser decreases to 30 W after traversing through 40 km of an optical fiber. Attenuation of the fiber in dB/km is therefore [10 log (166.7)]/40 0.56 dB/km. (dB) = 10 log10 (P1/P2) w.wang 23 The main cause of intrinsic absorption in the infrared region is the characteristic vibration frequency of atomic bonds. In silica glass, absorption is caused by the vibration of silicon-oxygen (Si-O) bonds. The interaction between the vibrating bond and the electromagnetic field of the optical signal causes intrinsic absorption. Light energy is transferred from the electromagnetic field to the bond. The tail of the infrared absorption band is shown in figure. w.wang 24 • Intrinsic attenuation is controlled by the fiber manufacturer • Absorption caused by water molecules and other impurities • Light strikes a molecule at the right angle and light energy is converted into heat • Absorption accounts for 3-5% of fiber attenuation these is near w.wangthe theoretical limit 25 Extrinsic Absorption Extrinsic Absorption. - Extrinsic absorption is caused by impurities introduced into the fiber material. Trace metal impurities, such as iron, nickel, and chromium, are introduced into the fiber during fabrication. Extrinsic absorption is caused by the electronic transition of these metal ions from one energy level to another. Extrinsic absorption also occurs when hydroxyl ions (OH-) are introduced into the fiber. Water in silica glass forms a silicon-hydroxyl (Si-OH) bond. This bond has a fundamental absorption at 2700 nm. However, the harmonics or overtones of the fundamental absorption occur in the region of operation. These harmonics increase extrinsic absorption at 1383 nm, 1250 nm, and 950 nm. Last figure shows the presence of the three OH- harmonics. The level of the OH- harmonic absorption is also indicated. These absorption peaks define three regions or windows of preferred operation. The first window is centered at 850 nm. The second window is centered at 1300 nm. The third window is centered at 1550 nm. Fiber optic systems operate at wavelengths defined by one of these windows. The amount of water (OH-) impurities present in a fiber should be less than a few parts per billion. Fiber attenuation caused by extrinsic absorption is affected by the level of impurities (OH-) present in the fiber. If the amount of impurities in a fiber is reduced, then fiber attenuation is reduced. w.wang 26 w.wang 27 w.wang 28 w.wang 29 w.wang 30 w.wang 31 w.wang 32 w.wang 33 w.wang 34 w.wang 35 Radiation loss due to bending straight Small bend Large bend w.wang 36 w.wang 37 w.wang 38 Extrinsic attenuation can be controlled by the cable installer w.wang 39 Macrobend loss Radiation attenuation coefficient is t= c1exp (-c2R) Where R is radius of curvature, c1 and c2 are constants independent of R Large bending loss tends to occurs at critical radius Rc 2 2 2 3/2 Rc~ 3n1 / (4(n1 -n2 ) ) Loss maybe reduced by -large relative refractive index difference -Operating at shortest wavelength possible w.wang 40 Fiber bend losses • Bend losses can be approximated using a combination of raytracing results (H. Lambrecht, et.al.) • Validation through optical path measurements 90° bend X axis: NA fiber Y axis: bending radius Blue color = high losses (source: H. Lambrecht) w.wang 41 • Microbends may not be visible with the naked eye • Microbends may be: o bend related o temperature related o tensile related w.wang o crush related 42 Microbend Loss Microbends are caused by small discontinuities or imperfections in the fiber. Uneven coating applications and improper cabling procedures increase microbend loss. External forces are also a source of microbends. An external force deforms the cabled jacket surrounding the fiber but causes only a small bend in the fiber. Microbends change the path that propagating modes take, as shown in figure. Microbend loss increases attenuation because low-order modes become coupled with high-order modes that are naturally lossy. w.wang 43 Total loss due to Scattering Absorption and Radiation w.wang 44 w.wang 45 Coupling Loss w.wang 46 w.wang Cleaving the waveguide 47 Measure only overall light loss w.wang 48 Dispersion w.wang 49 Dispersion w.wang 50 w.wang 51 DISPERSION There are two different types of dispersion in optical fibers. The types are intramodal and intermodal dispersion. Intramodal, or chromatic dispersion occurs in all types of fibers. Intermodal, or modal, dispersion occurs only in multimode fibers.
Load more

Recommended publications
  • Contents 1 Properties of Optical Systems
    Contents 1 Properties of Optical Systems ............................................................................................................... 7 1.1 Optical Properties of a Single Spherical Surface ........................................................................... 7 1.1.1 Planar Refractive Surfaces .................................................................................................... 7 1.1.2 Spherical Refractive Surfaces ................................................................................................ 7 1.1.3 Reflective Surfaces .............................................................................................................. 10 1.1.4 Gaussian Imaging Equation ................................................................................................. 11 1.1.5 Newtonian Imaging Equation.............................................................................................. 13 1.1.6 The Thin Lens ...................................................................................................................... 13 1.2 Aperture and Field Stops ............................................................................................................ 14 1.2.1 Aperture Stop Definition ..................................................................................................... 14 1.2.2 Marginal and Chief Rays ...................................................................................................... 14 1.2.3 Vignetting ...........................................................................................................................
    [Show full text]
  • Lecture 26 Dielectric Slab Waveguides
    Lecture 26 Dielectric Slab Waveguides In this lecture you will learn: • Dielectric slab waveguides •TE and TM guided modes in dielectric slab waveguides ECE 303 – Fall 2005 – Farhan Rana – Cornell University TE Guided Modes in Parallel-Plate Metal Waveguides r E()rr = yˆ E sin()k x e− j kz z x>0 o x x Ei Ei r r Ey k E r k i r kr i H Hi i z ε µo Hr r r ki = −kx xˆ + kzzˆ kr = kx xˆ + kzzˆ Guided TE modes are TE-waves bouncing back and fourth between two metal plates and propagating in the z-direction ! The x-component of the wavevector can have only discrete values – its quantized m π k = where : m = 1, 2, 3, x d KK ECE 303 – Fall 2005 – Farhan Rana – Cornell University 1 Dielectric Waveguides - I Consider TE-wave undergoing total internal reflection: E i x ε1 µo r k E r i r kr H θ θ i i i z r H r ki = −kx xˆ + kzzˆ r kr = kx xˆ + kzzˆ Evanescent wave ε2 µo ε1 > ε2 r E()rr = yˆ E e− j ()−kx x +kz z + yˆ ΓE e− j (k x x +kz z) 2 2 2 x>0 i i kz + kx = ω µo ε1 Γ = 1 when θi > θc When θ i > θ c : kx = − jα x r E()rr = yˆ T E e− j kz z e−α x x 2 2 2 x<0 i kz − α x = ω µo ε2 ECE 303 – Fall 2005 – Farhan Rana – Cornell University Dielectric Waveguides - II x ε2 µo Evanescent wave cladding Ei E ε1 µo r i r k E r k i r kr i core Hi θi θi Hi ε1 > ε2 z Hr cladding Evanescent wave ε2 µo One can have a guided wave that is bouncing between two dielectric interfaces due to total internal reflection and moving in the z-direction ECE 303 – Fall 2005 – Farhan Rana – Cornell University 2 Dielectric Slab Waveguides W 2d Assumption: W >> d x cladding y core
    [Show full text]
  • High Gain Slotted Waveguide Antenna Based on Beam Focusing Using Electrically Split Ring Resonator Metasurface Employing Negative Refractive Index Medium
    Progress In Electromagnetics Research C, Vol. 79, 115–126, 2017 High Gain Slotted Waveguide Antenna Based on Beam Focusing Using Electrically Split Ring Resonator Metasurface Employing Negative Refractive Index Medium Adel A. A. Abdelrehim and Hooshang Ghafouri-Shiraz* Abstract—In this paper, a new high performance slotted waveguide antenna incorporated with negative refractive index metamaterial structure is proposed, designed and experimentally demonstrated. The metamaterial structure is constructed from a multilayer two-directional structure of electrically split ring resonator which exhibits negative refractive index in direction of the radiated wave propagation when it is placed in front of the slotted waveguide antenna. As a result, the radiation beams of the slotted waveguide antenna are focused in both E and H planes, and hence the directivity and the gain are improved, while the beam area is reduced. The proposed antenna and the metamaterial structure operating at 10 GHz are designed, optimized and numerically simulated by using CST software. The effective parameters of the eSRR structure are extracted by Nicolson Ross Weir (NRW) algorithm from the s-parameters. For experimental verification, a proposed antenna operating at 10 GHz is fabricated using both wet etching microwave integrated circuit technique (for the metamaterial structure) and milling technique (for the slotted waveguide antenna). The measurements are carried out in an anechoic chamber. The measured results show that the E plane gain of the proposed slotted waveguide antenna is improved from 6.5 dB to 11 dB as compared to the conventional slotted waveguide antenna. Also, the E plane beamwidth is reduced from 94.1 degrees to about 50 degrees.
    [Show full text]
  • Waveguide Direction User Manual
    WaveGuide Direction Ex. Certified User Manual WaveGuide Direction Ex. Certified User Manual Applicable for product no. WG-DR40-EX Related to software versions: wdr 4.#-# Version 4.0 21st of November 2016 Radac B.V. Elektronicaweg 16b 2628 XG Delft The Netherlands tel: +31(0)15 890 3203 e-mail: [email protected] website: www.radac.nl Preface This user manual and technical documentation is intended for engineers and technicians involved in the software and hardware setup of the Ex. certified version of the WaveGuide Direction. Note All connections to the instrument must be made with shielded cables with exception of the mains. The shielding must be grounded in the cable gland or in the terminal compartment on both ends of the cable. For more information regarding wiring and cable specifications, please refer to Chapter 2. Legal aspects The mechanical and electrical installation shall only be carried out by trained personnel with knowledge of the local requirements and regulations for installation of electronic equipment. The information in this installation guide is the copyright property of Radac BV. Radac BV disclaims any responsibility for personal injury or damage to equipment caused by: Deviation from any of the prescribed procedures. • Execution of activities that are not prescribed. • Neglect of the general safety precautions for handling tools and use of electricity. • The contents, descriptions and specifications in this installation guide are subject to change without notice. Radac BV accepts no responsibility for any errors that may appear in this user manual. Additional information Please do not hesitate to contact Radac or its representative if you require additional information.
    [Show full text]
  • Instruction Manual Waveguide & Waveguide Server
    Instruction manual WaveGuide & WaveGuide Server Radac bv Elektronicaweg 16b 2628 XG DELFT Phone: +31 15 890 32 03 Email: [email protected] www.radac.n l Instruction manual WaveGuide + WaveGuide Server Version 4.1 2 of 30 Oct 2013 Instruction manual WaveGuide + WaveGuide Server Version 4.1 3 of 30 Oct 2013 Instruction manual WaveGuide + WaveGuide Server Table of Contents Introduction...................................................................................................................................................................4 Installation.....................................................................................................................................................................5 The WaveGuide Sensor...........................................................................................................................................5 CaBling.....................................................................................................................................................................6 The WaveGuide Server............................................................................................................................................7 Commissioning the system...........................................................................................................................................9 Connect the WGS to a computer.............................................................................................................................9 Authorization.........................................................................................................................................................10
    [Show full text]
  • Analysis of a Waveguide-Fed Metasurface Antenna
    Analysis of a Waveguide-Fed Metasurface Antenna Smith, D., Yurduseven, O., Mancera, L. P., Bowen, P., & Kundtz, N. B. (2017). Analysis of a Waveguide-Fed Metasurface Antenna. Physical Review Applied, 8(5). https://doi.org/10.1103/PhysRevApplied.8.054048 Published in: Physical Review Applied Document Version: Publisher's PDF, also known as Version of record Queen's University Belfast - Research Portal: Link to publication record in Queen's University Belfast Research Portal Publisher rights © 2017 American Physical Society. This work is made available online in accordance with the publisher’s policies. Please refer to any applicable terms of use of the publisher. General rights Copyright for the publications made accessible via the Queen's University Belfast Research Portal is retained by the author(s) and / or other copyright owners and it is a condition of accessing these publications that users recognise and abide by the legal requirements associated with these rights. Take down policy The Research Portal is Queen's institutional repository that provides access to Queen's research output. Every effort has been made to ensure that content in the Research Portal does not infringe any person's rights, or applicable UK laws. If you discover content in the Research Portal that you believe breaches copyright or violates any law, please contact [email protected]. Download date:02. Oct. 2021 PHYSICAL REVIEW APPLIED 8, 054048 (2017) Analysis of a Waveguide-Fed Metasurface Antenna † † David R. Smith,* Okan Yurduseven, Laura Pulido Mancera, and Patrick Bowen Department of Electrical and Computer Engineering, Duke University, Durham, North Carolina 27708, USA Nathan B.
    [Show full text]
  • Chapter 19/ Optical Properties
    Chapter 19 /Optical Properties The four notched and transpar- ent rods shown in this photograph demonstrate the phenomenon of photoelasticity. When elastically deformed, the optical properties (e.g., index of refraction) of a photoelastic specimen become anisotropic. Using a special optical system and polarized light, the stress distribution within the speci- men may be deduced from inter- ference fringes that are produced. These fringes within the four photoelastic specimens shown in the photograph indicate how the stress concentration and distribu- tion change with notch geometry for an axial tensile stress. (Photo- graph courtesy of Measurements Group, Inc., Raleigh, North Carolina.) Why Study the Optical Properties of Materials? When materials are exposed to electromagnetic radia- materials, we note that the performance of optical tion, it is sometimes important to be able to predict fibers is increased by introducing a gradual variation and alter their responses. This is possible when we are of the index of refraction (i.e., a graded index) at the familiar with their optical properties, and understand outer surface of the fiber. This is accomplished by the mechanisms responsible for their optical behaviors. the addition of specific impurities in controlled For example, in Section 19.14 on optical fiber concentrations. 766 Learning Objectives After careful study of this chapter you should be able to do the following: 1. Compute the energy of a photon given its fre- 5. Describe the mechanism of photon absorption quency and the value of Planck’s constant. for (a) high-purity insulators and semiconduc- 2. Briefly describe electronic polarization that re- tors, and (b) insulators and semiconductors that sults from electromagnetic radiation-atomic in- contain electrically active defects.
    [Show full text]
  • Waveguide Propagation
    NTNU Institutt for elektronikk og telekommunikasjon Januar 2006 Waveguide propagation Helge Engan Contents 1 Introduction ........................................................................................................................ 2 2 Propagation in waveguides, general relations .................................................................... 2 2.1 TEM waves ................................................................................................................ 7 2.2 TE waves .................................................................................................................... 9 2.3 TM waves ................................................................................................................. 14 3 TE modes in metallic waveguides ................................................................................... 14 3.1 TE modes in a parallel-plate waveguide .................................................................. 14 3.1.1 Mathematical analysis ...................................................................................... 15 3.1.2 Physical interpretation ..................................................................................... 17 3.1.3 Velocities ......................................................................................................... 19 3.1.4 Fields ................................................................................................................ 21 3.2 TE modes in rectangular waveguides .....................................................................
    [Show full text]
  • Nikon Binocular Handbook
    THE COMPLETE BINOCULAR HANDBOOK While Nikon engineers of semiconductor-manufactur- FINDING THE ing equipment employ our optics to create the world’s CONTENTS PERFECT BINOCULAR most precise instrumentation. For Nikon, delivering a peerless vision is second nature, strengthened over 4 BINOCULAR OPTICS 101 ZOOM BINOCULARS the decades through constant application. At Nikon WHAT “WATERPROOF” REALLY MEANS FOR YOUR NEEDS 5 THE RELATIONSHIP BETWEEN POWER, Sport Optics, our mission is not just to meet your THE DESIGN EYE RELIEF, AND FIELD OF VIEW The old adage “the better you understand some- PORRO PRISM BINOCULARS demands, but to exceed your expectations. ROOF PRISM BINOCULARS thing—the more you’ll appreciate it” is especially true 12-14 WHERE QUALITY AND with optics. Nikon’s goal in producing this guide is to 6-11 THE NUMBERS COUNT QUANTITY COUNT not only help you understand optics, but also the EYE RELIEF/EYECUP USAGE LENS COATINGS EXIT PUPIL ABERRATIONS difference a quality optic can make in your appre- REAL FIELD OF VIEW ED GLASS AND SECONDARY SPECTRUMS ciation and intensity of every rare, special and daily APPARENT FIELD OF VIEW viewing experience. FIELD OF VIEW AT 1000 METERS 15-17 HOW TO CHOOSE FIELD FLATTENING (SUPER-WIDE) SELECTING A BINOCULAR BASED Nikon’s WX BINOCULAR UPON INTENDED APPLICATION LIGHT DELIVERY RESOLUTION 18-19 BINOCULAR OPTICS INTERPUPILLARY DISTANCE GLOSSARY DIOPTER ADJUSTMENT FOCUSING MECHANISMS INTERNAL ANTIREFLECTION OPTICS FIRST The guiding principle behind every Nikon since 1917 product has always been to engineer it from the inside out. By creating an optical system specific to the function of each product, Nikon can better match the product attri- butes specifically to the needs of the user.
    [Show full text]
  • Waveguides Waveguides, Like Transmission Lines, Are Structures Used to Guide Electromagnetic Waves from Point to Point. However
    Waveguides Waveguides, like transmission lines, are structures used to guide electromagnetic waves from point to point. However, the fundamental characteristics of waveguide and transmission line waves (modes) are quite different. The differences in these modes result from the basic differences in geometry for a transmission line and a waveguide. Waveguides can be generally classified as either metal waveguides or dielectric waveguides. Metal waveguides normally take the form of an enclosed conducting metal pipe. The waves propagating inside the metal waveguide may be characterized by reflections from the conducting walls. The dielectric waveguide consists of dielectrics only and employs reflections from dielectric interfaces to propagate the electromagnetic wave along the waveguide. Metal Waveguides Dielectric Waveguides Comparison of Waveguide and Transmission Line Characteristics Transmission line Waveguide • Two or more conductors CMetal waveguides are typically separated by some insulating one enclosed conductor filled medium (two-wire, coaxial, with an insulating medium microstrip, etc.). (rectangular, circular) while a dielectric waveguide consists of multiple dielectrics. • Normal operating mode is the COperating modes are TE or TM TEM or quasi-TEM mode (can modes (cannot support a TEM support TE and TM modes but mode). these modes are typically undesirable). • No cutoff frequency for the TEM CMust operate the waveguide at a mode. Transmission lines can frequency above the respective transmit signals from DC up to TE or TM mode cutoff frequency high frequency. for that mode to propagate. • Significant signal attenuation at CLower signal attenuation at high high frequencies due to frequencies than transmission conductor and dielectric losses. lines. • Small cross-section transmission CMetal waveguides can transmit lines (like coaxial cables) can high power levels.
    [Show full text]
  • A Rack-Mounted Precision Waveguide-Below-Cutoff Attenuator with an Absolute Electronic Readout
    NBSIR 74-394 A RACK-MOUNTED PRECISION WAVEGUIDE-BELOW-CUTOFF ATTENUATOR WITH AN ABSOLUTE ELECTRONIC READOUT Clarence C. Cook Electromagnetics Division Institute for Basic Standards National Bureau of Standards Boulder, Colorado 80302 November 1974 Prepared for Jet Propulsion Laboratory Pasadena, California 91103 NBSIR 74-394 A RACK-MOUNTED PRECISION WAVEGUIDE-BELOW-CUTOFF ATTENUATOR WITH AN ABSOLUTE ELECTRONIC READOUT Clarence C. Cook Electromagnetics Division Institute for Basic Standards National Bureau of Standards Boulder, Colorado 80302 Certain commerical equipment and materials are identified on the drawings in order to adequately specify the fabrication procedure. In no case does such identification imply recommendation or endorse- ment by the National Bureau of Standards, nor does it imply that the material or equipment identified is necessarily the best available for the purpose. November 1974 Prepared for Jet Propulsion Laboratory Pasadena, California 91103 u s DEPARTMENT OF COMMERCE, Frederick B. Dent. Secretary NATIONAL BUREAU OF STANDARDS Richard W Roberts Director CONTENTS Page ABSTRACT 1 1. INTRODUCTION 1 2. THEORY OF OPERATION 1 3. DESCRIPTION OF ATTENUATOR 3 4. ATTENUATOR OPERATION 7 4.1 Preliminary Setup and Check 7 4.2 Displacement Readouts and Attenuation Value 7 5. OPERATIONAL CONSIDERATIONS 9 5.1 Initial Alignment 9 . 5.2 Operation 10 6. ERROR ANALYSIS , . 11 6.1 Waveguide Diameter 11 6.2 Waveguide Conductivity .... 12 6.3 Attenuation Rate 12 6.4 Displacement Readout 13 6.5 Miscellaneous Sources of Error 13 6.6 Temperature Effects . 15 6.7 Summary of Errors 16 7. SUMMARY 16 8. ACKNOWLEDGMENTS 17 9. REFERENCES 17 10. PARTS LIST 18 iii LIST OF FIGURES Page 1.
    [Show full text]
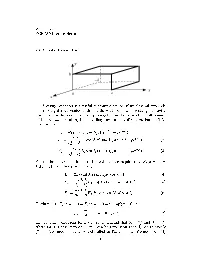
  • 23. Cavity Resonator
    WCChew ECE Lecture Notes Cavity Resonator y b –d x 0 a z A cavity resonator is a useful microwave device If we close o two ends of a rectangular waveguide with metallic walls we have a rectangular cavity resonator In this case the wave propagating in the zdirection will b ounce o the twowalls resulting in a standing waveinthezdirection For the TM casewe have j z j z z z E E sin x sin y e e z x y j x z j z j z z z E cos x sin y e e E x y x y x j y z j z j z z z E E sin x cos y e e y x y y x For the b oundary conditions to be satised we require that E z x E z Hence and y E E sin xsin y cos z z x y z x z E E cos x sin y sin z x x y z x y y z E E sin x cos y sin z y x y z x y Furthermore E z dE z d implying that x y p p z d m n The guidance conditions for a waveguide demand that and x y a b where for TM case neither m or n can be zero Now that has to satisfy z the TM mo de in a cavity is classied as TM mo de We note from mnp that p can be zero while E Hence the TM cavity mo de can exist z mn In order for and to b e solutions to the wave equation we require that m n p x y z a b d For a given choice of m n and p only a single frequency can satisfy This frequency is the resonant frequency of the cavity It is only at this frequency that the cavity can sustain a free oscillation At other frequencies the elds interfere destructively and the free oscillation is not sustained From we gather that the resonant frequency for the TM
    [Show full text]