DOCSLIB.ORG

Variance on Topics of Plane Geometry

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Variance on Topics of Plane Geometry $5 251251 \\ 3 &[ 'D(DD ( D % VARIANCE ON TOPICS OF PLANE GEOMETRY ,RQ3ăWUDúFX)ORUHQWLQ6PDUDQGDFKH 9$5,$1&(21723,&6 2)3/$1(*(20(75< (GXFDWLRQDO3XEOLVKLQJ 2013 1 Education Publishing 1313 Chesapeake Avenue Columbus, Ohio 43212 USA Tel. (614) 485-0721 &RS\ULJKWE\3XEOLVKHUDQG$XWKRUV 3HHU5HYLHZHUV Marius Coman, researcher, Bucharest, Romania. Prof. Valeri Kroumov, Okayama University of Science, Japan. Said Broumi, University of Hassan II Mohammedia, Casablanca, Morocco. Dr. Ştefan Vlăduţescu, University of Craiova, Romania. Many books can be downloaded from the following 'LJLWDO/LEUDU\RI6FLHQFH: http://fs.gallup.unm.edu/eBooks-otherformats.htm ($1 ,6%1 2 &217(176 9$5,$1&(21723,&62)3/$1(*(20(75< 3UHIDFH 4XDVL,VRJRQDO&HYLDQV 1HGLDQVDQG7ULDQJOHVZLWKWKH6DPH&RHIILFLHQWRI'HIRUPDWLRQ )URPD3UREOHPRI*HRPHWULFDO&RQVWUXFWLRQWRWKH&DUQRW&LUFOHV 7KH3RODURID3RLQWZLWK5HVSHFWWRD&LUFOH 6HYHUDO0HWULFDO5HODWLRQV5HJDUGLQJWKH$QWL%LVHFWRUWKH$QWL6\PPHGLDQWKH$QWL +HLJKWDQGWKHLU,VRJRQDO $Q ,PSRUWDQW $SSOLFDWLRQ RI WKH &RPSXWDWLRQ RI WKH 'LVWDQFHV EHWZHHQ 5HPDUNDEOH 3RLQWVLQWKH7ULDQJOH*HRPHWU\ 7KH'XDOLW\DQGWKH(XOHU¶V/LQH 7ZR$SSOLFDWLRQVRI'HVDUJXHV¶7KHRUHP $Q$SSOLFDWLRQRI6RQGDW¶V7KHRUHP5HJDUGLQJWKH2UWKRKRPRORJLFDO7ULDQJOHV $QRWKHU3URRIRIWKHD7KHRUHP5HODWLYHWRWKH2UWKRORJLFDO7ULDQJOHV 7ZR 7ULDQJOHV ZLWK WKH 6DPH 2UWKRFHQWHU DQG D 9HFWRU 3URRI RI 6WHYDQRYLF¶V 7KHRUHP 7ZR5HPDUNDEOH2UWKR+RPRORJLFDO7ULDQJOHV $*HQHUDOL]DWLRQRI&HUWDLQ5HPDUNDEOH3RLQWVRIWKH7ULDQJOH*HRPHWU\ *HQHUDOL]DWLRQRID5HPDUNDEOH7KHRUHP 3DQWD]L¶V7KHRUHP5HJDUGLQJWKH%L2UWKRORJLFDO7ULDQJOHV $1HZ3URRIDQGDQ$SSOLFDWLRQRI'HUJLDGHV¶7KHRUHP 0L[W/LQHDU&LUFOHV$GMRLQWO\([,QVFULEHG$VVRFLDWHGWRD7ULDQJOH 3 $3URSHUW\RIWKH&LUFXPVFULEHG2FWDJRQ )URP1HZWRQ¶V7KHRUHPWRD7KHRUHPRIWKH,QVFULEDEOH2FWDJRQ 7ULSOHWVRI7UL+RPRORJLFDO7ULDQJOHV $&ODVVRI2UWKR+RPRORJLFDO7ULDQJOHV 4 3UHIDFH This book contains 21 papers of plane geometry. It deals with various topics, such as: quasi-isogonal cevians, nedians, polar of a point with respect to a circle, anti-bisector, aalsonti-symmedian, anti-height and their isogonal. A nedian is a line segment that has its origin in a triangle’s vertex and divides the opposite side in Q equal segments. The papers also study distances between remarkable points in the 2D-geometry, the circumscribed octagon and the inscribable octagon, the circles adjointly ex-inscribed associated to a triangle, and several classical results such as: Carnot circles, Euler’s line, Desargues theorem, Sondat’s theorem, Dergiades theorem, Stevanovic’s theorem, Pantazi’s theorem, and Newton’s theorem. Special attention is given in this book to RUWKRORJLFDO WULDQJOHV ELRUWKRORJLFDO WULDQJOHV RUWKRKRPRORJLFDOWULDQJOHVand WULKRPRORJLFDOWULDQJOHV The notion of “ortho-homological triangles” was introduced by the Belgium mathematician Joseph Neuberg in 1922 in the journal Mathesis and it characterizes the triangles that are simultaneously orthogonal (i.e. the sides of one triangle are perpendicular to the sides of the other triangle) and homological. We call this “ortho-homological of first type” in order to distinguish it from our next notation. In our articles, we gave the same denomination “ortho-homological triangles” to triangles that are simultaneously orthological and homological. We call it “ortho-homological of second type.” Each paper is independent of the others. Yet, papers on the same or similar topics are listed together one after the other. This book is a continuation of the previous book 7KH*HRPHWU\RI+RPRORJLFDO7ULDQJOHV, by Florentin Smarandache and Ion Pătraşcu, Educ. Publ., Ohio, USA, 244 p., 2012. The book is intended for College and University students and instructors that prepare for mathematical competitions such as National and International Mathematical Olympiads, or the AMATYC (American Mathematical Association for Two Year Colleges) student competition, or Putnam competition, Gheorghe Ţiteica Romanian student competition, and so on. The book is also useful for geometrical researchers. The authors 5 4XDVL,VRJRQDO&HYLDQV 3URIHVVRU,RQ3ăWUDúFX±1DWLRQDO&ROOHJH)UD܊LL%X]HúWL&UDLRYD5RPDQLD 3URIHVVRU)ORUHQWLQ6PDUDQGDFKH±8QLYHUVLW\RI1HZ0H[LFR86$ ,Q WKLV DUWLFOH ZH ZLOO LQWURGXFH WKH TXDVLLVRJRQDO &HYLDQV DQG ZH¶OO HPSKDVL]H RQ WULDQJOHVLQZKLFKWKHKHLJKWDQGWKHPHGLDQDUHTXDVLLVRJRQDO&HYLDQV )RUEHJLQQLQJZH¶OOUHFDOO 'HILQLWLRQ ,Q D WULDQJOH $%& WKH &HYLDQV $' , $( DUH FDOOHG LVRJRQDO LI WKHVH DUH V\PPHWULF LQ UDSSRUWWRWKHDQJOH $ ELVHFWRU 2EVHUYDWLRQ ,QILJXUHDUHUHSUHVHQWHGWKHLVRJRQDO&HYLDQV $' , $( $$ ' %' (& % &( )LJ,VRJRQDO&HYLDQV 3URSRVLWLRQ ,QDWULDQJOH $%& WKHKHLJKW $' DQGWKHUDGLXV $2 RIWKHFLUFXPVFULEHGFLUFOHDUH LVRJRQDO&HYLDQV 'HILQLWLRQ :HFDOOWKH&HYLDQV $' , $( LQWKHWULDQJOH $%& TXDVLLVRJRQDOLIWKHSRLQW % LV EHWZHHQWKHSRLQWV ' DQG ( WKHSRLQW ( LVEHWZHHQWKHSRLQWV % DQG& ,DQG ))'$% ($& . 2EVHUYDWLRQ ,QILJXUHZHUHSUHVHQWHGWKHTXDVLLVRJRQDO&HYLDQV $'$( . ϲ $ ' & %( )LJTXDVLLVRJRQDO&HYLDQV 3URSRVLWLRQ 7KHUHDUHWULDQJOHVLQZKLFKWKHKHLJKWDQGWKHPHGLDQDUHTXDVLLVRJRQDO&HYLDQV 3URRI ,WLVFOHDUWKDWLIZHORRNIRUWULDQJOHV $%& IRUZKLFKWKHKHLJKWDQGWKHPHGLDQIURPWKH SRLQW $ DUHTXDVLLVRJRQDOWKHQWKHVHPXVWEHREWXVHDQJOHGWULDQJOH:H¶OOFRQVLGHUVXFKD FDVHLQZKLFK P$) 4 VHHILJXUH $5 25 1 \ 3 &[ ' D(D % )LJ /HW2 WKHFHQWHURIWKHFLUFXPVFULEHGWULDQJOHZHQRWHZLWK 1 WKHGLDPHWULFSRLQWRI $ DQGZLWK 3 WKHLQWHUVHFWLRQRIWKHOLQH $2 ZLWK %& :HFRQVLGHUNQRZQWKHUDGLXV 5 RIWKHFLUFOHDQG %&3 D , D52 DQGZHWU\WR FRQVWUXFWWKHWULDQJOH $%& LQZKLFKWKHKHLJKW $' DQGWKHPHGLDQ $( DUHTXDVLLVRJRQDO &HYLDQVWKHUHIRUH ))'$% ($& .7KLVWULDQJOHFDQEHFRQVWUXFWHGLIZHILQGWKHOHQJWKV 3& DQG 31 LQIXQFWLRQRI D DQG 5 .:HQRWH 3&33 [31 \ . ϳ :HFRQVLGHUWKHSRZHURIWKHSRLQW 3 LQIXQFWLRQRIWKHFLUFOHC 25 ,WUHVXOWVWKDW [¬![D 3¬!\\ 5 )URPWKH3URSHUW\ZHKDYHWKDW ))'$% 2$& .2QWKHRWKHUVLGH ))2$& 2&$ DQG $'$( DUHTXDVLLVRJRQDOZHREWDLQWKDW2&& $( . 7KH7KDOHV¶WKHRUHPLPSOLHVWKDW [ \5! 3 D5 6XEVWLWXWLQJ [ IURP LQ ZHREWDLQWKHHTXDWLRQ D5\## 55D\D5 #!3 7KHGLVFULPLQDQWRIWKLVHTXDWLRQLV ǻ3#!55 D5D (YLGHQWO\ ǻ4 ,WKHUHIRUHWKHHTXDWLRQKDVWZRUHDOVROXWLRQV D5 %HFDXVHWKHSURGXFWRIWKHVROXWLRQVLV DQGLWLVQHJDWLYHZHREWDLQWKDWRQHRI D5# VROXWLRQVLVVWULFWO\SRVLWLYH)RUWKLVSRVLWLYHYDOXHRI \ ZHILQGWKHYDOXHRI [ FRQVHTXHQWO\ ZHFDQFRQVWUXFWWKHSRLQW 3 ,WKHQWKHSRLQW 1 DQGDWWKHLQWHUVHFWLRQRIWKHOLQH 31 ZHILQG $ DQGWKHUHIRUHWKHWULDQJOH $%& LVFRQVWUXFWHG )RUH[DPSOHLIZHFRQVLGHU 5 3 DQG D 3 ,ZHREWDLQWKHWULDQJOH $%& LQZKLFK $% 3 , %& 3 DQG $& 3!. :HOHDYHWRRXUUHDGHUVWRYHULI\WKDWWKHKHLJKWDQGWKHPHGLDQIURPWKHSRLQW $ DUH TXDVLLVRJRQDO ϴ 1HGLDQVDQG7ULDQJOHVZLWKWKH6DPH&RHIILFLHQWRI'HIRUPDWLRQ ,RQ3ăWUDúFX±1DWLRQDO&ROOHJH)UD܊LL%X]HúWL&UDLRYD5RPDQLD )ORUHQWLQ6PDUDQGDFKH±8QLYHUVLW\RI1HZ0H[LFR*DOOXS1086$ ,Q>@'U)ORUHQWLQ6PDUDQGDFKHJHQHUDOL]HGVHYHUDOSURSHUWLHVRIWKHQHGLDQV+HUHZH ZLOOFRQWLQXHWKHVHULHVRIWKHVHUHVXOWVDQGZLOOHVWDEOLVKFHUWDLQFRQQHFWLRQVZLWKWKHWULDQJOHV ZKLFKKDYHWKHVDPHFRHIILFLHQWRIGHIRUPDWLRQ 'HILQLWLRQ 7KHOLQHVHJPHQWVWKDWKDYHWKHLURULJLQLQWKHWULDQJOH¶VYHUWH[DQGGLYLGHWKHRSSRVLWH VLGHLQ Q HTXDOVHJPHQWVDUHFDOOHGQHGLDQV :HFDOOWKHQHGLDQ $$L EHLQJRIRUGHU L (L1£ ),LQWKHWULDQJOH $%& LI $L GLYLGHVWKH L JJJGL JJJG JJJGL JJJG VLGH %& LQWKHUDSSRUW %$%&3¬ RU&$3¬ &% xxLQ # Q L Q L Q 2EVHUYDWLRQ 7KHPHGLDQVRIDWULDQJOHDUHQHGLDQVRIRUGHULQWKHFDVHZKHQ Q 3 WKHVHDUHFDOOHG WHUWLDQ :H¶OOUHFDOOIURP>@WKHIROORZLQJ 3URSRVLWLRQ 8VLQJWKHQHGLDQVRIWKHVDPHRIDWULDQJOHZHFDQFRQVWUXFWDWULDQJOH 3URSRVLWLRQ 7KHVXPRIWKHVTXDUHVRIWKHOHQJWKVRIWKHQHGLDQVRIRUGHU L RIDWULDQJOH $%& LVJLYHQ E\WKHIROORZLQJUHODWLRQ LLQQ#! $$!! %% && 3DEF !! LLL Q :H¶OOSURYH 3URSRVLWLRQ 7KHVXPRIWKHVTXDUHVRIWKHOHQJWKVRIWKHVLGHVRIWKHWULDQJOH $%& GHWHUPLQHGE\ WKHLQWHUVHFWLRQRIWKHQHGLDQVRIRUGHUL RIWKHWULDQJOH $%& LVJLYHQE\WKHIROORZLQJUHODWLRQ QL# $ %%&&$!!3 DEF !! LLQQ#! $ &L $ &%L % % & )LJ $L :HQRWHG q$s 333&&LL $$ q %s $$ LL %% q &s %% L && L. 3URRI :H¶OODSSO\WKH0HQHODXV¶WKHRUHPLQWKHWULDQJOH $$&L IRU WKH WUDQVYHUVDOV %%## %L VHH)LJ %$ % & % $ LL¬¬ 3 %& %LL $ % $ LD LE Q# L E %HFDXVH %$333 %& % $ , IURP LWUHVXOWVWKDW LLQQ L Q Q Q# L % $$3 $ LLQQ#! L 7KH0HQHODXV¶WKHRUHPDSSOLHGLQWKHWULDQJOH $$%L IRUWKHWUDQVYHUVDO &&## &L JLYHV &$ & % $ $ LL¬¬ 3 &% &LL $ $ $ Q## L D Q L F LF %XW &$333 & % & $ ZKLFKVXEVWLWXWHGLQ JLYHV LLQQQ L LQ $$$3 $ LLQQ#! L ,WLVREVHUYHGWKDW $%$%$$3# DQGXVLQJWKHUHODWLRQ DQG ZHILQG QQ# L $% 3 $$ LLQQ#! L 6LPLODUO\ZHREWDLQ QQ# L %& 3 %% (8) LLQQ#! L QQ# L &$3 && LLQQ#! L 8VLQJWKHUHODWLRQV DQG DIWHUDFRXSOHRIFRPSXWDWLRQVZHREWDLQWKHUHODWLRQ 2EVHUYDWLRQ 7KHWULDQJOHIRUPHGE\WKHQHGLDQVRIRUGHU L DVVLGHVLVVLPLODUZLWKWKHWULDQJOHIRUPHG E\WKHLQWHUVHFWLRQVRIWKHQHGLDQVRIRUGHUL ,QGHHG WKH UHODWLRQV DQG VKRZ WKDW WKH VLGHV $% % & & $ DUH SURSRUWLRQDOZLWK $$LL %% && L 7KH5XVVLDQPDWKHPDWLFLDQ99/HEHGHYLQWURGXFHVLQ>@WKHQRWLRQRIFRHIILFLHQWRI GHIRUPDWLRQRIDWULDQJOH7RGHILQHWKLVQRWLRQZHQHHGDFRXSOHRIGHILQLWLRQVDQGREVHUYDWLRQV 'HILQLWLRQ ,I $%& LV D WULDQJOH DQG LQ LWV H[WHULRU RQ LWV VLGHV DUH FRQVWUXFWHG WKH HTXLODWHUDO WULDQJOHV %&$ &$% $%& WKHQWKHHTXLODWHUDOWULDQJOH 222IRUPHGE\WKHFHQWHUVRIWKH FLUFXPVFULEHGFLUFOHVWRWKHHTXLODWHUDOWULDQJOHVGHVFULEHGDERYHLVFDOOHGWKHH[WHULRUWULDQJOH RI1DSROHRQ ,IWKHHTXLODWHUDOWULDQJOHV %&$ &$% $%& LQWHUVHFWLQWKHLQWHULRURIWKHWULDQJOH $%& WKHQ WKH HTXLODWHUDO WULDQJOH 222 IRUPHG E\ WKH FHQWHUV RI WKH FLUFXPVFULEHG FLUFOHV WR WKHVHWULDQJOHVLVFDOOHGWKHLQWHULRUWULDQJOHRI1DSROHRQ % $ 2 & 2 % & 2 $ )LJ $¶ $ 2¶ 2¶ %2¶&¶ & %¶ )LJ 2EVHUYDWLRQ ,QILJXUHLVUHSUHVHQWHGWKHH[WHUQDOWULDQJOHRI1DSROHRQDQGLQILJXUHLVUHSUHVHQWHG WKHLQWHULRUWULDQJOHRI1DSROHRQ 'HILQLWLRQ $FRHIILFLHQWRIGHIRUPDWLRQRIDWULDQJOHLVWKHUDSSRUWEHWZHHQWKHVLGHRIWKHLQWHULRU
Load more

Recommended publications
  • Volume 6 (2006) 1–16
    FORUM GEOMETRICORUM A Journal on Classical Euclidean Geometry and Related Areas published by Department of Mathematical Sciences Florida Atlantic University b bbb FORUM GEOM Volume 6 2006 http://forumgeom.fau.edu ISSN 1534-1178 Editorial Board Advisors: John H. Conway Princeton, New Jersey, USA Julio Gonzalez Cabillon Montevideo, Uruguay Richard Guy Calgary, Alberta, Canada Clark Kimberling Evansville, Indiana, USA Kee Yuen Lam Vancouver, British Columbia, Canada Tsit Yuen Lam Berkeley, California, USA Fred Richman Boca Raton, Florida, USA Editor-in-chief: Paul Yiu Boca Raton, Florida, USA Editors: Clayton Dodge Orono, Maine, USA Roland Eddy St. John’s, Newfoundland, Canada Jean-Pierre Ehrmann Paris, France Chris Fisher Regina, Saskatchewan, Canada Rudolf Fritsch Munich, Germany Bernard Gibert St Etiene, France Antreas P. Hatzipolakis Athens, Greece Michael Lambrou Crete, Greece Floor van Lamoen Goes, Netherlands Fred Pui Fai Leung Singapore, Singapore Daniel B. Shapiro Columbus, Ohio, USA Steve Sigur Atlanta, Georgia, USA Man Keung Siu Hong Kong, China Peter Woo La Mirada, California, USA Technical Editors: Yuandan Lin Boca Raton, Florida, USA Aaron Meyerowitz Boca Raton, Florida, USA Xiao-Dong Zhang Boca Raton, Florida, USA Consultants: Frederick Hoffman Boca Raton, Floirda, USA Stephen Locke Boca Raton, Florida, USA Heinrich Niederhausen Boca Raton, Florida, USA Table of Contents Khoa Lu Nguyen and Juan Carlos Salazar, On the mixtilinear incircles and excircles,1 Juan Rodr´ıguez, Paula Manuel and Paulo Semi˜ao, A conic associated with the Euler line,17 Charles Thas, A note on the Droz-Farny theorem,25 Paris Pamfilos, The cyclic complex of a cyclic quadrilateral,29 Bernard Gibert, Isocubics with concurrent normals,47 Mowaffaq Hajja and Margarita Spirova, A characterization of the centroid using June Lester’s shape function,53 Christopher J.
    [Show full text]
  • Sava Grozdev and Deko Dekov, the Lester Circle Is Orthogonal to The
    Journal of Computer-Generated Mathematics Problem 6 The Lester circle is orthogonal to the Orthocentroidal Circle of the Triangle of the Orthocenters of the Triangulation Triangles of the Tarry Point. Sava Grozdev and Deko Dekov Submitted on May 1, 2014 Publication Date: July 10, 2014 At the present time, there are seven notable circles known to be orthogonal to the Lester circle. See [1]. The below problem introduces a new notable circle which is orthogonal to the Lester circle. Prove the following problem, produced by the computer program “Discoverer”: Problem 6. Given ABC . The Lester circle of ABC is the circle passing through the circumcenter, nine-point center and the outer Fermat point. The Tarry point P is the intersection point of the circumcircle and the line passing through the centroid and the midpoint of the circumcenter and the Lemoine (Symmedian) point. Let D, E and F are the orthocenters of triangles PBC , PCA and PAB , respectively, G is the centroid of DEF and H is the orthocenter of DEF . Prove that the circle having as diameter the segment GH is orthogonal to the Lester circle. Short form of the problem: Problem 6. Prove that the Lester circle is orthogonal to the Orthocentroidal Circle of the Triangle of the Orthocenters of the Triangulation Triangles of the Tarry Point. The reader may find the definitions in [2-5]. Please submit the solution of the problem for publication in this journal to the editor of this journal: [email protected] See the figure: Journal of Computer-Generated Mathematics 2014 Problem no 4 Page 1 of 3 In the figure: c – Lester circle, P – Tarry Point, D – Orthocenter of Triangle PBC, E – Orthocenter of Triangle PCA, F – Orthocenter of Triangle PAB, c1 – Orthocentroidal Circle of Triangle DEF, Circle c1 is orthogonal to the Lester circle.
    [Show full text]
  • Steiner's Hat: a Constant-Area Deltoid Associated with the Ellipse
    STEINER’S HAT: A CONSTANT-AREA DELTOID ASSOCIATED WITH THE ELLIPSE RONALDO GARCIA, DAN REZNIK, HELLMUTH STACHEL, AND MARK HELMAN Abstract. The Negative Pedal Curve (NPC) of the Ellipse with respect to a boundary point M is a 3-cusp closed-curve which is the affine image of the Steiner Deltoid. Over all M the family has invariant area and displays an array of interesting properties. Keywords curve, envelope, ellipse, pedal, evolute, deltoid, Poncelet, osculat- ing, orthologic. MSC 51M04 and 51N20 and 65D18 1. Introduction Given an ellipse with non-zero semi-axes a,b centered at O, let M be a point in the plane. The NegativeE Pedal Curve (NPC) of with respect to M is the envelope of lines passing through points P (t) on the boundaryE of and perpendicular to [P (t) M] [4, pp. 349]. Well-studied cases [7, 14] includeE placing M on (i) the major− axis: the NPC is a two-cusp “fish curve” (or an asymmetric ovoid for low eccentricity of ); (ii) at O: this yielding a four-cusp NPC known as Talbot’s Curve (or a squashedE ellipse for low eccentricity), Figure 1. arXiv:2006.13166v5 [math.DS] 5 Oct 2020 Figure 1. The Negative Pedal Curve (NPC) of an ellipse with respect to a point M on the plane is the envelope of lines passing through P (t) on the boundary,E and perpendicular to P (t) M. Left: When M lies on the major axis of , the NPC is a two-cusp “fish” curve. Right: When− M is at the center of , the NPC is 4-cuspE curve with 2-self intersections known as Talbot’s Curve [12].
    [Show full text]
  • Proceedings of the Indiana Academy of Science
    104 CoLLiNEAR Sets of Three Points Connected With the Triangle. By Robert J. A ley. This paper does not claim to be either original or complete. It contains a fairly complete list of collinear sets connected with the triangle. All cases of collinearity connected with polygons of more than three sides have been omitted. The subject of collinearity is both interesting and fruitful. There are three well defined methods of proving the collinearity of three points. The classic one is the application of the theorem of Menelaus: "If I), E, F are points on the sides B C, C A, A B respectfully of AB (', such that B DXCEXA F = — D CXE AXF B, then D, E, F are collinear." In many cases the data are insufficient for the u.se of this method. Another method of frequent use is to prove that the angle formed by the three points is a straight angle. The author has used another method, believed to be original with him, when the points in question are such that the ratios of their distances from the sides can be determined. This method is fully illustrated in " Contributions to the (Jeometry of the Triangle." Collinear prolilems fall into two very well marked classes. The first class is made up of those points which are definitely located with respect to the triangle. The second class is made up of those points which are located with reference to some auxiliary point. notation. In order to save time in the enunciation of propositions the following notation will be used : A B C is the fundamental triangle.
    [Show full text]
  • Circles Containing the Parry Point
    International Journal of Computer Discovered Mathematics (IJCDM) ISSN 2367-7775 c IJCDM March 2016, Volume 1, No.1, pp.11-14. Received 15 October 2015. Published on-line 1 December 2015 web: http://www.journal-1.eu/ c The Author(s) This article is published with open access1. Mathematics Discovered by Computers: Circles Containing the Parry Point Sava Grozdeva and Deko Dekovb2 a VUZF University of Finance, Business and Entrepreneurship, Gusla Street 1, 1618 Sofia, Bulgaria e-mail: [email protected] bZahari Knjazheski 81, 6000 Stara Zagora, Bulgaria e-mail: [email protected] web: http://www.ddekov.eu/ Abstract. We present new remarkable circles containing the Parry point. The results are discovered by the computer program "Discoverer". Keywords. Parry point, remarkable circle, mathematics discovered by comput- ers, triangle geometry, remarkable point, “Discoverer”. Mathematics Subject Classification (2010). 51-04, 68T01, 68T99. 1. Introduction The computer program “Discoverer”, created by Grozdev and Dekov, is the first computer program, able easily to discover new theorems in mathematics, and possibly, the first computer program, able easily to discover new knowledge in science. See [3]. In this paper, by using the “Discoverer”, we investigate the circles containing the Parry point. We find 23 different remarkable circles containing the Parry Point. We expect that the majority of results are new, discovered by a computer. Recall that the Parry Point is the point on the circumcircle of triangle ABC, other than the Steiner point, and on the line connecting the Centroid and the Steiner Point. The Parry point is labeled X(111) in the Kimberling’s Encyclopedia of Triangle Centers ETC [4].
    [Show full text]
  • Volume 7 2007
    FORUM GEOMETRICORUM A Journal on Classical Euclidean Geometry and Related Areas published by Department of Mathematical Sciences Florida Atlantic University b b b FORUM GEOM Volume 7 2007 http://forumgeom.fau.edu ISSN 1534-1178 Editorial Board Advisors: John H. Conway Princeton, New Jersey, USA Julio Gonzalez Cabillon Montevideo, Uruguay Richard Guy Calgary, Alberta, Canada Clark Kimberling Evansville, Indiana, USA Kee Yuen Lam Vancouver, British Columbia, Canada Tsit Yuen Lam Berkeley, California, USA Fred Richman Boca Raton, Florida, USA Editor-in-chief: Paul Yiu Boca Raton, Florida, USA Editors: Clayton Dodge Orono, Maine, USA Roland Eddy St. John’s, Newfoundland, Canada Jean-Pierre Ehrmann Paris, France Chris Fisher Regina, Saskatchewan, Canada Rudolf Fritsch Munich, Germany Bernard Gibert St Etiene, France Antreas P. Hatzipolakis Athens, Greece Michael Lambrou Crete, Greece Floor van Lamoen Goes, Netherlands Fred Pui Fai Leung Singapore, Singapore Daniel B. Shapiro Columbus, Ohio, USA Steve Sigur Atlanta, Georgia, USA Man Keung Siu Hong Kong, China Peter Woo La Mirada, California, USA Technical Editors: Yuandan Lin Boca Raton, Florida, USA Aaron Meyerowitz Boca Raton, Florida, USA Xiao-Dong Zhang Boca Raton, Florida, USA Consultants: Frederick Hoffman Boca Raton, Floirda, USA Stephen Locke Boca Raton, Florida, USA Heinrich Niederhausen Boca Raton, Florida, USA Table of Contents Joseph Stern, Euler’s triangle determination problem, 1 Christopher Bradley, David Monk, and Geoff Smith, On a porism associated with the Euler and Droz-Farny lines, 11 Yu-Dong Wu and Zhi-Hua Zhang, The edge-tangent sphere of a circumscriptible tetrahedron, 19 Melissa Baker and Robert Powers, A stronger triangle inequality for neutral geometry, 25 Jingcheng Tong and Sidney Kung, A simple construction of the golden ratio, 31 Tom M.
    [Show full text]
  • Lester Circles
    International Journal of Computer Discovered Mathematics (IJCDM) ISSN 2367-7775 c IJCDM March 2016, Volume 1, No.1, pp.15-25. Received 15 October 2015. Published on-line 15 December 2015 web: http://www.journal-1.eu/ c The Author(s) This article is published with open access1. Computer Discovered Mathematics: Lester Circles Sava Grozdeva and Deko Dekovb2 a VUZF University of Finance, Business and Entrepreneurship, Gusla Street 1, 1618 Sofia, Bulgaria e-mail: [email protected] bZahari Knjazheski 81, 6000 Stara Zagora, Bulgaria e-mail: [email protected] web: http://www.ddekov.eu/ Abstract. A circle is a Lester circle, if it contains at least four remarkable points of the triangle. By using the computer program “Discoverer”, we investigate Lester circles. Keywords. Lester circle, remarkable point, triangle geometry, computer- discovered mathematics, Euclidean geometry, “Discoverer”. Mathematics Subject Classification (2010). 51-04, 68T01, 68T99. 1. Introduction From the June Lester web site [8]: “There is always a circle through three given points, as long as they are not on a line. Circles through four given points - those are exceptional. Especially when the four points are well-known special points of a triangle.” June Lester has investigated the circle on which the Circumcenter, Nine-Point Center, and the Outer and Inner Fermat points lie. Now this circle is known as the Lester circle. See [9], [11, Lester Circle], [12, Lester’s theorem]. In 2002 Bernard Gibert [2] discovered that the point Alrescha, that is, point X(1117) in the Kimberling’s ETC [7], also lies on the Lester circle. In 2014 Grozdev and Dekov discovered, with the help of the computer program “Discoverer”, three new remarkable points which lie on the Lester circle.
    [Show full text]
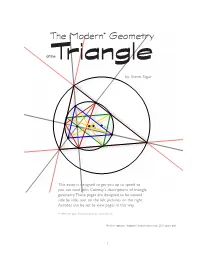
  • The Modern* Geometry of Trianglethe
    The Modern* Geometry of Trianglethe by Steve Sigur A G O H P B C This essay is designed to get you up to speed so you can read John Conway's descriptions of triangle geometry. These pages are designed to be viewed side by side, text on the left, pictures on the right. Acrobat can be set to view pages in this way. © 1999 Steve Sigur. Permission given for non-profit use. *In this context "modern" means less than 200 years old 1 In school we learn a geometry of equalities, based on quantities being exactly equal in some way. But many of the structures in geometry are not best expressed distances, angles, or congruencies. In this little essay, I try to present a more modern view of triangle geometry based on the appreciation of structures in and about tri- angles. To do this we start with the most fundamental properties of points and lines—properties that arise from nothing other than “pointness” and “lineness” — and proceed to “turn on” other aspects a few at a time. This is not a formal exposition and everything here is presented without proof. Nor is it thorough. I only want to give those interested in geometry the perceptual and vocabulary background to be able to follow Conway’s posting about geometry. I suggest that you play with each topic; draw the pictures, find relationships, prove theorems. Steve The dual nature of points and lines We begin by going to the core of geometry. We are going to “turn off” most properties we usually use and keep only two.
    [Show full text]
  • The Modern Geometry of the Triangle
    H^^fe',- -"*' V^ A W Af* 5Mi (Qantell luiuersity Htbrary Stljaca, New fork BOUGHT WITH THE INCOME OF THE SAGE ENDOWMENT FUND THE GIFT OF HENRY W. SAGE 1891 Mathematics* Cornell University Library QA 482.G16 1910 The modern geometry of the triangle. 3 1924 001 522 782 The original of this book is in the Cornell University Library. There are no known copyright restrictions in the United States on the use of the text. http://www.archive.org/details/cu31924001522782 THE MODERN GEOMETRY OF THE TRIANGLE. BY WILLIAM GALLATLY, MA. SECOND EDITION. /<?ro London : FRANCIS HODGSON, 89 Faebingdon Street, E.G. •S a. Ms^-rm — PREFACE. In this little treatise on the Geometry of the Triangle are presented some of the more important researches on the subject which have been undertaken during the last thirty years. The author ventures to express not merely his hope, but his con- fident expectation, that these novel and interesting theorems some British, but the greater part derived from French and German sources—will widen the outlook of our mathematical instructors and lend new vigour to their teaching. The book includes some articles contributed by the present writer to the Educational Times Reprint, to whose editor he would offer his sincere thanks for the great encouragement which he has derived from such recognition. He is also most grateful to Sir George Greenhill, Prof. A. C. Dixon, Mr. V. R. Aiyar, Mr. W. F. Beard, Mr. R. F. Davis, and Mr. E. P. Rouse for permission to use the theorems due to them. W. G.
    [Show full text]
  • Paul Yiu's Introduction to the Geometry of the Triangle
    Introduction to the Geometry of the Triangle Paul Yiu Summer 2001 Department of Mathematics Florida Atlantic University Version 12.1224 December 2012 Contents 1 The Circumcircle and the Incircle 1 1.1 Preliminaries.............................. 1 1.1.1 Coordinatizationofpointsonaline . 1 1.1.2 Centersofsimilitudeoftwocircles . 2 1.1.3 Harmonicdivision ....................... 2 1.1.4 MenelausandCevaTheorems . 3 1.1.5 Thepowerofapointwithrespecttoacircle . 4 1.2 Thecircumcircleandtheincircleofatriangle . .... 5 1.2.1 Thecircumcircle ........................ 5 1.2.2 Theincircle........................... 5 1.2.3 The centers of similitude of (O) and (I) ............ 6 1.2.4 TheHeronformula....................... 8 1.3 Euler’sformulaandSteiner’sporism . 10 1.3.1 Euler’sformula......................... 10 1.3.2 Steiner’sporism ........................ 10 1.4 Appendix:Mixtilinearincircles . 12 2 The Euler Line and the Nine-point Circle 15 2.1 TheEulerline ............................. 15 2.1.1 Homothety ........................... 15 2.1.2 Thecentroid .......................... 15 2.1.3 Theorthocenter......................... 16 2.2 Thenine-pointcircle... .... ... .... .... .... .... 17 2.2.1 TheEulertriangleasamidwaytriangle . 17 2.2.2 Theorthictriangleasapedaltriangle . 17 2.2.3 Thenine-pointcircle . 18 2.2.4 Triangles with nine-point center on the circumcircle ..... 19 2.3 Simsonlinesandreflections. 20 2.3.1 Simsonlines .......................... 20 2.3.2 Lineofreflections .... ... .... .... .... .... 20 2.3.3 Musselman’s Theorem: Point with
    [Show full text]
  • Hexyl-Anticevian Triangles
    International Journal of Computer Discovered Mathematics (IJCDM) ISSN 2367-7775 c IJCDM November 2015, Volume 0, No.0, pp.60-69. Received 15 July 2015. Published on-line 15 September 2015 web: http://www.journal-1.eu/ c The Author(s) This article is published with open access1. Computer Discovered Mathematics: Hexyl-Anticevian Triangles Sava Grozdeva and Deko Dekovb2 a VUZF University of Finance, Business and Entrepreneurship, Gusla Street 1, 1618 Sofia, Bulgaria e-mail: [email protected] bZahari Knjazheski 81, 6000 Stara Zagora, Bulgaria e-mail: [email protected] web: http://www.ddekov.eu/ Abstract. We introduce the notion of a Hexyl-anticevian triangle of a point P . The known Hexyl triangle coincides with the Hexyl-anticevian triangle of the Incenter. In this paper we present theorems about the Hexyl-anticevian triangle of a point P , and we also consider the special cases when P is the Incenter or the Centroid. All theorems and problems in this paper are discovered by the computer program “Discoverer”. Theorems about other special cases, e.g. when P is the Circumcenter, Orthocenter, Symmedian Point, and so on, could be easily discovered by the “Discoverer” upon request. Keywords. hexyl triangle, hexyl-antimedial triangle, triangle geometry, remark- able point, computer-discovered mathematics, Euclidean geometry, “Discoverer”. Mathematics Subject Classification (2010). 51-04, 68T01, 68T99. 1. Introduction The computer program “Discoverer”, created by the authors, is the first computer program, able easily to discover new theorems in mathematics, and possibly, the first computer program, able easily to discover new knowledge in science. See [4]. In this paper, by using the “Discoverer”, we investigate the hexyl-anticevian trian- gles.
    [Show full text]
  • The Geometry of Homological Triangles
    FLORENTIN SMARANDACHE ION PĂTRAŞCU THE GEOMETRY OF HOMOLOGICAL TRIANGLES 2012 1 Table of Contents Preface ..………………………………………………………………………………………………………………………………………………….5 Chapter 1 ....................................................................................................................................................... 6 Remarkable pairs of homological triangles .................................................................................................. 6 1.1. Homological triangles’ theorem ......................................................................................................... 6 1.2. Some remarkable homological triangles .......................................................................................... 15 A. The orthic triangle .......................................................................................................................... 15 B. The Cevian triangle ........................................................................................................................ 17 C. The anti-supplemental triangle ....................................................................................................... 18 D. The K-symmedian triangle ............................................................................................................. 19 E. The tangential triangle .................................................................................................................... 23 F. The contact triangle .......................................................................................................................
    [Show full text]