DOCSLIB.ORG

Volume 6 (2006) 1–16

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Volume 6 (2006) 1–16 FORUM GEOMETRICORUM A Journal on Classical Euclidean Geometry and Related Areas published by Department of Mathematical Sciences Florida Atlantic University b bbb FORUM GEOM Volume 6 2006 http://forumgeom.fau.edu ISSN 1534-1178 Editorial Board Advisors: John H. Conway Princeton, New Jersey, USA Julio Gonzalez Cabillon Montevideo, Uruguay Richard Guy Calgary, Alberta, Canada Clark Kimberling Evansville, Indiana, USA Kee Yuen Lam Vancouver, British Columbia, Canada Tsit Yuen Lam Berkeley, California, USA Fred Richman Boca Raton, Florida, USA Editor-in-chief: Paul Yiu Boca Raton, Florida, USA Editors: Clayton Dodge Orono, Maine, USA Roland Eddy St. John’s, Newfoundland, Canada Jean-Pierre Ehrmann Paris, France Chris Fisher Regina, Saskatchewan, Canada Rudolf Fritsch Munich, Germany Bernard Gibert St Etiene, France Antreas P. Hatzipolakis Athens, Greece Michael Lambrou Crete, Greece Floor van Lamoen Goes, Netherlands Fred Pui Fai Leung Singapore, Singapore Daniel B. Shapiro Columbus, Ohio, USA Steve Sigur Atlanta, Georgia, USA Man Keung Siu Hong Kong, China Peter Woo La Mirada, California, USA Technical Editors: Yuandan Lin Boca Raton, Florida, USA Aaron Meyerowitz Boca Raton, Florida, USA Xiao-Dong Zhang Boca Raton, Florida, USA Consultants: Frederick Hoffman Boca Raton, Floirda, USA Stephen Locke Boca Raton, Florida, USA Heinrich Niederhausen Boca Raton, Florida, USA Table of Contents Khoa Lu Nguyen and Juan Carlos Salazar, On the mixtilinear incircles and excircles,1 Juan Rodr´ıguez, Paula Manuel and Paulo Semi˜ao, A conic associated with the Euler line,17 Charles Thas, A note on the Droz-Farny theorem,25 Paris Pamfilos, The cyclic complex of a cyclic quadrilateral,29 Bernard Gibert, Isocubics with concurrent normals,47 Mowaffaq Hajja and Margarita Spirova, A characterization of the centroid using June Lester’s shape function,53 Christopher J. Bradley and Geoff C. Smith, The locations of triangle centers,57 Christopher J. Bradley and Geoff C. Smith, The locations of the Brocard points,71 Floor van Lamoen, Archimedean adventures,79 Anne Fontaine and Susan Hurley, Proof by picture: Products and reciprocals of diagonals length ratios in the regular polygon,97 Hiroshi Okumura and Masayuki Watanabe, A generalization of Power’s Archimedean circles, 103 Stanley Rabinowitz, Pseudo-incircles, 107 Wilson Stothers, Grassmann cubics and desmic structures, 117 Matthew Hudelson, Concurrent medians of (2n +1)-gons, 139 Dieter Ruoff, On the generating motions and the convexity of a well-known curve in hyperbolic geometry, 149 Mowaffaq Hajja, A very short and simple proof of “the most elementary theorem” of euclidean geometry, 167 S´andor Kiss, The orthic-of-intouch and intouch-of-orthic triangles, 171 Kurt Hofstetter, A 4-step construction of the golden ratio, 179 Eisso J. Atzema, A theorem by Giusto Bellavitis on a class of quadrilaterals, 181 Wladimir Boskoff and Bogdan Suceav˘a, A projectivity characterized by the Pythagorean relation, 187 Bogdan Suceav˘a and Paul Yiu, The Feuerbach point and Euler lines, 191 Eric Danneels, A simple perspectivity, 199 Quang Tuan Bui, Pedals on circumradii and the Jerabek center, 205 Bernard Gibert, The Simmons conics, 213 Nikolaos Dergiades, A synthetic proof and generalization of Bellavitis’ theorem, 225 Huub van Kempen, On some theorems of Poncelet and Carnot, 229 Charles Thas, The Droz-Farny theorem and related topics, 235 Zvonko Cerin,ˇ On butterflies inscribed in a quadrilateral, 241 Eric Danneels, On triangles with vertices on the angle bisectors, 247 Matthew Hudelson, Formulas among diagonals in the regular polygon and the Catalan numbers, 255 Khoa Lu Nguyen, A note on the barycentric square root of Kiepert perspectors, 263 Clark Kimberling, Translated triangle perspective to a reference triangle, 269 James L. Parish, On the derivative of a vertex polynomial, 285 Alexei Myakishev, On two remarkable lines related to a quadrilateral, 289 Max A. Tran Intersecting circles and their inner tangent circle, 297 K. R. S. Sastry, Two Brahmagupta problems, 301 Floor van Lamoen, Square wreaths around hexagons, 311 Jean-Pierre Ehrmann, Some geometric constructions, 327 Amy Bell, Hansen’s right triangle theorem, its converse and a generalization, 335 Paul Yiu, Some constructions related to the Kiepert hyperbola, 343 Author Index, 359 Forum Geometricorum b Volume 6 (2006) 1–16. bbb FORUM GEOM ISSN 1534-1178 On Mixtilinear Incircles and Excircles Khoa Lu Nguyen and Juan Carlos Salazar Abstract. A mixtilinear incircle (respectively excircle) of a triangle is tangent to two sides and to the circumcircle internally (respectively externally). We study the configuration of the three mixtilinear incircles (respectively excircles). In particular, we give easy constructions of the circle (apart from the circumcircle) tangent the three mixtilinear incircles (respectively excircles). We also obtain a number of interesting triangle centers on the line joining the circumcenter and the incenter of a triangle. 1. Preliminaries In this paper we study two triads of circles associated with a triangle, the mix- tilinear incircles and the mixtilinear excircles. For an introduction to these circles, see [4] and §§2, 3 below. In this section we collect some important basic results used in this paper. Proposition 1 (d’Alembert’s Theorem [1]). Let O1(r1), O2(r2), O3(r3) be three circles with distinct centers. According as ε =+1or −1, denote by A1ε, A2ε, A3ε respectively the insimilicenters or exsimilicenters of the pairs of circles ((O2), (O3)), ((O3), (O1)), and ((O1), (O2)).Forεi = ±1, i =1, 2, 3, the points A1ε1 , A2ε2 and A3ε3 are collinear if and only if ε1ε2ε3 = −1. See Figure 1. The insimilicenter and exsimilicenter of two circles are respectively their inter- nal and external centers of similitude. In terms of one-dimensional barycentric coordinates, these are the points r2 · O1 + r1 · O2 ins(O1(r1),O2(r2)) = , (1) r1 + r2 −r2 · O1 + r1 · O2 exs(O1(r1),O2(r2)) = . (2) r1 − r2 Proposition 2. Let O1(r1), O2(r2), O3(r3) be three circles with noncollinears cen- ters. For ε = ±1, let Oε(rε) be the Apollonian circle tangent to the three circles, all externally or internally according as ε =+1or −1. Then the Monge line con- taining the three exsimilicenters exs(O2(r2),O3(r3)), exs(O3(r3),O1(r1)), and exs(O1(r1),O2(r2)) is the radical axis of the Apollonian circles (O+) and (O−). See Figure 1. Publication Date: January 18, 2006. Communicating Editor: Paul Yiu. The authors thank Professor Yiu for his contribution to the last section of this paper. 2 K. L. Nguyen and J. C. Salazar A3− A2− O1 A2+ A3+ O+ O− A1− O2 A1+ O3 Figure 1. Lemma 3. Let BC be a chord of a circle O(r). Let O1(r1) be a circle that touches BC at E and intouches the circle (O) at D. The line DE passes through the midpoint A of the arc BC that does not contain the point D. Furthermore, AD · AE = AB2 = AC2. Proposition 4. The perspectrix of the circumcevian triangle of P is the polar of P with respect to the circumcircle. Let ABC be a triangle with circumcenter O and incenter I. For the circumcircle and the incircle, r · O + R · I ins((O), (I)) = = X55, R + r −r · O + R · I exs((O), (I)) = = X56. R − r in the notations of [3]. We also adopt the following notations. A0 point of tangency of incircle with BC A1 intersection of AI with the circumcircle A2 antipode of A1 on the circumcircle Similarly define B0, B1, B2, C0, C1 and C2. Note that (i) A0B0C0 is the intouch triangle of ABC, (ii) A1B1C1 is the circumcevian triangle of the incenter I, On mixtilinear incircles and excircles 3 (iii) A2B2C2 is the medial triangle of the excentral triangle, i.e., A2 is the midpoint between the excenters Ib and Ic. It is also the midpoint of the arc BAC of the circumcircle. 2. Mixtilinear incircles The A-mixtilinear incircle is the circle (Oa) that touches the rays AB and AC at Ca and Ba and the circumcircle (O) internally at X. See Figure 2. Define the B- and C-mixtilinear incircles (Ob) and (Oc) analogously, with points of tangency Y and Z with the circumcircle. See [4]. We begin with an alternative proof of the main result of [4]. Proposition 5. The lines AX, BY , CZ are concurrent at exs((O), (I)). Proof. Since A =exs((Oa), (I)) and X =exs((O), (Oa)), the line AX passes through exs((O), (I)) by d’Alembert’s Theorem. For the same reason, BY and CZ also pass through the same point. A2 Y A A B1 B0 O b C1 O O c Ba Ba Z I C0 I Ca Oa Ca Oa B C B A0 C X X A1 Figure 2 Figure 3 Lemma 6. (1) I is the midpoint of BaCa. = r (2) The A-mixtilinear incircle has radius ra cos2 A . 2 (3) XI bisects angle BXC. See Figure 3. Consider the radical axis a of the mixtilinear incircles (Ob) and (Oc). Proposition 7. The radical axis a contains (1) the midpoint A1 of the arc BC of (O) not containing the vertex A, (2) the midpoint Ma of IA0, where A0 is the point of tangency of the incircle with the side BC. 4 K. L. Nguyen and J. C. Salazar Y A B1 Bc Cb B0 O C1 b Mb Oc Z C0 I Mc Ma B Ac A0 Ab C A1 Figure 4. Proof. (1) By Lemma 3, Z, Ac and A1 are collinear, so are Y , Ab, A1. Also, 2 2 A1Ac · A1Z = A1B = A1C = A1Ab · A1Y . This shows that A1 is on the radical axis of (Ob) and (Oc). (2) Consider the incircle (I) and the B-mixtilinear incircle (Ob) with common ex-tangents BA and BC. Since the circle (I) touches BA and BC at C0 and A0, and the circle (Ob) touches the same two lines at Cb and Ab, the radical axis of these two circles is the line joining the midpoints of CbC0 and AbA0.
Load more

Recommended publications
  • The Stammler Circles
    Forum Geometricorum b Volume 2 (2002) 151–161. bbb FORUM GEOM ISSN 1534-1178 The Stammler Circles Jean-Pierre Ehrmann and Floor van Lamoen Abstract. We investigate circles intercepting chords of specified lengths on the sidelines of a triangle, a theme initiated by L. Stammler [6, 7]. We generalize his results, and concentrate specifically on the Stammler circles, for which the intercepts have lengths equal to the sidelengths of the given triangle. 1. Introduction Ludwig Stammler [6, 7] has investigated, for a triangle with sidelengths a, b, c, circles that intercept chords of lengths µa, µb, µc (µ>0) on the sidelines BC, CA and AB respectively. He called these circles proportionally cutting circles,1 and proved that their centers lie on the rectangular hyperbola through the circumcenter, the incenter, and the excenters. He also showed that, depending on µ, there are 2, 3 or 4 circles cutting chords of such lengths. B0 B A0 C A C0 Figure 1. The three Stammler circles with the circumtangential triangle As a special case Stammler investigated, for µ =1, the three proportionally cutting circles apart from the circumcircle. We call these the Stammler circles. Stammler proved that the centers of these circles form an equilateral triangle, cir- cumscribed to the circumcircle and homothetic to Morley’s (equilateral) trisector Publication Date: November 22, 2002. Communicating Editor: Bernard Gibert. 1Proportionalschnittkreise in [6]. 152 J.-P. Ehrmann and F. M. van Lamoen triangle. In fact this triangle is tangent to the circumcircle at the vertices of the circumtangential triangle. 2 See Figure 1. In this paper we investigate the circles that cut chords of specified lengths on the sidelines of ABC, and obtain generalizations of results in [6, 7], together with some further results on the Stammler circles.
    [Show full text]
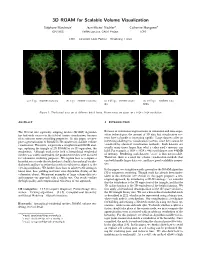
  • 3D ROAM for Scalable Volume Visualization
    3D ROAM for Scalable Volume Visualization St´ephane Marchesin∗ Jean-Michel Dischler† Catherine Mongenet‡ ICPS/IGG INRIA Lorraine, CALVI Project ICPS LSIIT { Universit´e Louis Pasteur { Strasbourg, France (a) 2.5 fps – 104000 tetrahedra (b) 1 fps – 380000 tetrahedra (c) 0.45 fps – 932000 tetrahe- (d) 0.15 fps – 3065000 tetra- dra hedra Figure 1: The bonsa¨ı data set at different detail levels. Frame rates are given for a 1024 × 1024 resolution ABSTRACT 1 INTRODUCTION The 2D real time optimally adapting meshes (ROAM) algorithm Because of continuous improvements in simulation and data acqui- has had wide success in the field of terrain visualization, because sition technologies, the amount of 3D data that visualization sys- of its efficient error-controlling properties. In this paper, we pro- tems have to handle is increasing rapidly. Large datasets offer an pose a generalization of ROAM in 3D suitable for scalable volume interesting challenge to visualization systems, since they cannot be visualization. Therefore, we perform a straightforward 2D/3D anal- visualized by classical visualization methods. Such datasets are ogy, replacing the triangle of 2D ROAM by its 3D equivalent, the usually many times larger than what a video card's memory can tetrahedron. Although work in the field of hierarchical tetrahedral hold. For example, a 1024×1024×446 voxel dataset uses 446MB meshes was widely undertaken, the produced meshes were not used of memory. Rendering such datasets ”as-is” is thus not possible. for volumetric rendering purposes. We explain how to compute a Therefore, there is a need for volume visualization methods that bounded error inside the tetrahedron to build a hierarchical tetrahe- can both handle larger data sets, and have good scalability proper- dral mesh and how to refine this mesh in real time to adapt it to the ties.
    [Show full text]
  • Configurations on Centers of Bankoff Circles 11
    CONFIGURATIONS ON CENTERS OF BANKOFF CIRCLES ZVONKO CERINˇ Abstract. We study configurations built from centers of Bankoff circles of arbelos erected on sides of a given triangle or on sides of various related triangles. 1. Introduction For points X and Y in the plane and a positive real number λ, let Z be the point on the segment XY such that XZ : ZY = λ and let ζ = ζ(X; Y; λ) be the figure formed by three mj utuallyj j tangenj t semicircles σ, σ1, and σ2 on the same side of segments XY , XZ, and ZY respectively. Let S, S1, S2 be centers of σ, σ1, σ2. Let W denote the intersection of σ with the perpendicular to XY at the point Z. The figure ζ is called the arbelos or the shoemaker's knife (see Fig. 1). σ σ1 σ2 PSfrag replacements X S1 S Z S2 Y XZ Figure 1. The arbelos ζ = ζ(X; Y; λ), where λ = jZY j . j j It has been the subject of studies since Greek times when Archimedes proved the existence of the circles !1 = !1(ζ) and !2 = !2(ζ) of equal radius such that !1 touches σ, σ1, and ZW while !2 touches σ, σ2, and ZW (see Fig. 2). 1991 Mathematics Subject Classification. Primary 51N20, 51M04, Secondary 14A25, 14Q05. Key words and phrases. arbelos, Bankoff circle, triangle, central point, Brocard triangle, homologic. 1 2 ZVONKO CERINˇ σ W !1 σ1 !2 W1 PSfrag replacements W2 σ2 X S1 S Z S2 Y Figure 2. The Archimedean circles !1 and !2 together.
    [Show full text]
  • Downloaded from Bookstore.Ams.Org 30-60-90 Triangle, 190, 233 36-72
    Index 30-60-90 triangle, 190, 233 intersects interior of a side, 144 36-72-72 triangle, 226 to the base of an isosceles triangle, 145 360 theorem, 96, 97 to the hypotenuse, 144 45-45-90 triangle, 190, 233 to the longest side, 144 60-60-60 triangle, 189 Amtrak model, 29 and (logical conjunction), 385 AA congruence theorem for asymptotic angle, 83 triangles, 353 acute, 88 AA similarity theorem, 216 included between two sides, 104 AAA congruence theorem in hyperbolic inscribed in a semicircle, 257 geometry, 338 inscribed in an arc, 257 AAA construction theorem, 191 obtuse, 88 AAASA congruence, 197, 354 of a polygon, 156 AAS congruence theorem, 119 of a triangle, 103 AASAS congruence, 179 of an asymptotic triangle, 351 ABCD property of rigid motions, 441 on a side of a line, 149 absolute value, 434 opposite a side, 104 acute angle, 88 proper, 84 acute triangle, 105 right, 88 adapted coordinate function, 72 straight, 84 adjacency lemma, 98 zero, 84 adjacent angles, 90, 91 angle addition theorem, 90 adjacent edges of a polygon, 156 angle bisector, 100, 147 adjacent interior angle, 113 angle bisector concurrence theorem, 268 admissible decomposition, 201 angle bisector proportion theorem, 219 algebraic number, 317 angle bisector theorem, 147 all-or-nothing theorem, 333 converse, 149 alternate interior angles, 150 angle construction theorem, 88 alternate interior angles postulate, 323 angle criterion for convexity, 160 alternate interior angles theorem, 150 angle measure, 54, 85 converse, 185, 323 between two lines, 357 altitude concurrence theorem,
    [Show full text]
  • Kaleidoscopic Symmetries and Self-Similarity of Integral Apollonian Gaskets
    Kaleidoscopic Symmetries and Self-Similarity of Integral Apollonian Gaskets Indubala I Satija Department of Physics, George Mason University , Fairfax, VA 22030, USA (Dated: April 28, 2021) Abstract We describe various kaleidoscopic and self-similar aspects of the integral Apollonian gaskets - fractals consisting of close packing of circles with integer curvatures. Self-similar recursive structure of the whole gasket is shown to be encoded in transformations that forms the modular group SL(2;Z). The asymptotic scalings of curvatures of the circles are given by a special set of quadratic irrationals with continued fraction [n + 1 : 1; n] - that is a set of irrationals with period-2 continued fraction consisting of 1 and another integer n. Belonging to the class n = 2, there exists a nested set of self-similar kaleidoscopic patterns that exhibit three-fold symmetry. Furthermore, the even n hierarchy is found to mimic the recursive structure of the tree that generates all Pythagorean triplets arXiv:2104.13198v1 [math.GM] 21 Apr 2021 1 Integral Apollonian gaskets(IAG)[1] such as those shown in figure (1) consist of close packing of circles of integer curvatures (reciprocal of the radii), where every circle is tangent to three others. These are fractals where the whole gasket is like a kaleidoscope reflected again and again through an infinite collection of curved mirrors that encodes fascinating geometrical and number theoretical concepts[2]. The central themes of this paper are the kaleidoscopic and self-similar recursive properties described within the framework of Mobius¨ transformations that maps circles to circles[3]. FIG. 1: Integral Apollonian gaskets.
    [Show full text]
  • A Note on the Miquel Points
    International Journal of Computer Discovered Mathematics (IJCDM) ISSN 2367-7775 c IJCDM September 2016, Volume 1, No.3, pp.45-49. Received 10 September 2016. Published on-line 20 September 2016 web: http://www.journal-1.eu/ c The Author(s) This article is published with open access1. Computer Discovered Mathematics: A Note on the Miquel Points Sava Grozdeva, Hiroshi Okumurab and Deko Dekovc 2 a VUZF University of Finance, Business and Entrepreneurship, Gusla Street 1, 1618 Sofia, Bulgaria e-mail: [email protected] b Department of Mathematics, Yamato University, Osaka, Japan e-mail: [email protected] cZahari Knjazheski 81, 6000 Stara Zagora, Bulgaria e-mail: [email protected] web: http://www.ddekov.eu/ Abstract. By using the computer program “Discoverer”, we give theorems about Miquel associate points. Abstract. Keywords. Miquel associate point, triangle geometry, remarkable point, computer-discovered mathematics, Euclidean geometry, Discoverer. Mathematics Subject Classification (2010). 51-04, 68T01, 68T99. 1. Introduction The computer program “Discoverer”, created by Grozdev and Dekov, with the collaboration by Professor Hiroshi Okumura, is the first computer program, able easily to discover new theorems in mathematics, and possibly, the first computer program, able easily to discover new knowledge in science. In this paper, by using the “Discoverer”, we investigate the Miquel points. The following theorem is known as the Miquel theorem: Theorem 1.1. If points A1;B1 and C1 are chosen on the sides BC; CA and AB of triangle ABC, then the circumcircles of triangles AB1C1; BC1A1 and CA1B1 have a point in common. 1This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
    [Show full text]
  • A Generalization of the Conway Circle
    Forum Geometricorum b Volume 13 (2013) 191–195. b b FORUM GEOM ISSN 1534-1178 A Generalization of the Conway Circle Francisco Javier Garc´ıa Capitan´ Abstract. For any point in the plane of the triangle we show a conic that be- comes the Conway circle in the case of the incenter. We give some properties of the conic and of the configuration of the six points that define it. Let ABC be a triangle and I its incenter. Call Ba the point on line CA in the opposite direction to AC such that ABa = BC = a and Ca the point on line BA in the opposite direction to AB such that ACa = a. Define Cb, Ab and Ac, Bc cyclically. The six points Ab, Ac, Bc, Ba, Ca, Cb lie in a circle called the Conway circle with I as center and squared radius r2 + s2 as indicated in Figure 1. This configuration also appeared in Problem 6 in the 1992 Iberoamerican Mathematical Olympiad. The problem asks to establish that the area of the hexagon CaBaAbCbBcAc is at least 13∆(ABC) (see [4]). Ca Ca Ba Ba a a a a A A C0 B0 I I r Ab Ac Ab Ac b B s − b s − c C c b B s − b s − c C c c c Bc Bc Cb Cb Figure 1. The Conway circle Figure 2 Figure 2 shows a construction of these points which can be readily generalized. The lines BI and CI intersect the parallel of BC through A at B0 and C0.
    [Show full text]
  • Coaxal Pencil of Circles and Spheres in the Pavillet Tetrahedron
    17TH INTERNATIONAL CONFERENCE ON GEOMETRY AND GRAPHICS ©2016 ISGG 4–8 AUGUST, 2016, BEIJING, CHINA COAXAL PENCILS OF CIRCLES AND SPHERES IN THE PAVILLET TETRAHEDRON Axel PAVILLET [email protected] ABSTRACT: After a brief review of the properties of the Pavillet tetrahedron, we recall a theorem about the trace of a coaxal pencil of spheres on a plane. Then we use this theorem to show a re- markable correspondence between the circles of the base and those of the upper triangle of a Pavillet tetrahedron. We also give new proofs and new point of view of some properties of the Bevan point of a triangle using solid triangle geometry. Keywords: Tetrahedron, orthocentric, coaxal pencil, circles, spheres polar 2 Known properties We first recall the notations and properties (with 1 Introduction. their reference) we will use in this paper (Fig.1). • The triangle ABC is called the base trian- gle and defines the base plane (horizontal). The orthocentric tetrahedron of a scalene tri- angle [12], named the Pavillet tetrahedron by • The incenter, I, is called the apex of the Richard Guy [8, Ch. 5] and Gunther Weiss [16], tetrahedron. is formed by drawing from the vertices A, B and 0 0 0 C of a triangle ABC, on an horizontal plane, • The other three vertices (A ,B ,C ) form a three vertical segments AA0 = AM = AL = x, triangle called the upper triangle and define BB0 = BK = BM = y, CC0 = CL = CK = z, a plane called the upper plane. where KLM is the contact triangle of ABC. We As a standard notation, all points lying on the denote I the incenter of ABC, r its in-radius, base plane will have (as much as possible) a 0 0 0 and consider the tetrahedron IA B C .
    [Show full text]
  • The Area of a Triangle
    Chapter 22 The area of a triangle 22.1 Heron’s formula for the area of a triangle Theorem 22.1. The area of a triangle of sidelengths a, b, c is given by = s(s a)(s b)(s c), △ − − − 1 p where s = 2 (a + b + c). B Ia I ra r A C Y Y ′ s − b s − c s − a Proof. Consider the incircle and the excircle on the opposite side of A. From the similarity of triangles AIZ and AI′Z′, r s a = − . ra s From the similarity of triangles CIY and I′CY ′, r r =(s b)(s c). · a − − 802 The area of a triangle From these, (s a)(s b)(s c) r = − − − , r s and the area of the triangle is = rs = s(s a)(s b)(s c). △ − − − p Exercise 1. Prove that 1 2 = (2a2b2 +2b2c2 +2c2a2 a4 b4 c4). △ 16 − − − 22.2 Heron triangles 803 22.2 Heron triangles A Heron triangle is an integer triangle whose area is also an integer. 22.2.1 The perimeter of a Heron triangle is even Proposition 22.2. The semiperimeter of a Heron triangle is an integer. Proof. It is enough to consider primitive Heron triangles, those whose sides are relatively prime. Note that modulo 16, each of a4, b4, c4 is congruent to 0 or 1, according as the number is even or odd. To render in (??) the sum 2a2b2 +2b2c2 +2c2a2 a4 b4 c4 0 modulo 16, exactly two of a, b, c must be odd. It− follows− that− the≡ perimeter of a Heron triangle must be an even number.
    [Show full text]
  • Geometry: Neutral MATH 3120, Spring 2016 Many Theorems of Geometry Are True Regardless of Which Parallel Postulate Is Used
    Geometry: Neutral MATH 3120, Spring 2016 Many theorems of geometry are true regardless of which parallel postulate is used. A neutral geom- etry is one in which no parallel postulate exists, and the theorems of a netural geometry are true for Euclidean and (most) non-Euclidean geomteries. Spherical geometry is a special case of Non-Euclidean geometries where the great circles on the sphere are lines. This leads to spherical trigonometry where triangles have angle measure sums greater than 180◦. While this is a non-Euclidean geometry, spherical geometry develops along a separate path where the axioms and theorems of neutral geometry do not typically apply. The axioms and theorems of netural geometry apply to Euclidean and hyperbolic geometries. The theorems below can be proven using the SMSG axioms 1 through 15. In the SMSG axiom list, Axiom 16 is the Euclidean parallel postulate. A neutral geometry assumes only the first 15 axioms of the SMSG set. Notes on notation: The SMSG axioms refer to the length or measure of line segments and the measure of angles. Thus, we will use the notation AB to describe a line segment and AB to denote its length −−! −! or measure. We refer to the angle formed by AB and AC as \BAC (with vertex A) and denote its measure as m\BAC. 1 Lines and Angles Definitions: Congruence • Segments and Angles. Two segments (or angles) are congruent if and only if their measures are equal. • Polygons. Two polygons are congruent if and only if there exists a one-to-one correspondence between their vertices such that all their corresponding sides (line sgements) and all their corre- sponding angles are congruent.
    [Show full text]
  • The Algebra of Projective Spheres on Plane, Sphere and Hemisphere
    Journal of Applied Mathematics and Physics, 2020, 8, 2286-2333 https://www.scirp.org/journal/jamp ISSN Online: 2327-4379 ISSN Print: 2327-4352 The Algebra of Projective Spheres on Plane, Sphere and Hemisphere István Lénárt Eötvös Loránd University, Budapest, Hungary How to cite this paper: Lénárt, I. (2020) Abstract The Algebra of Projective Spheres on Plane, Sphere and Hemisphere. Journal of Applied Numerous authors studied polarities in incidence structures or algebrization Mathematics and Physics, 8, 2286-2333. of projective geometry [1] [2]. The purpose of the present work is to establish https://doi.org/10.4236/jamp.2020.810171 an algebraic system based on elementary concepts of spherical geometry, ex- tended to hyperbolic and plane geometry. The guiding principle is: “The Received: July 17, 2020 Accepted: October 27, 2020 point and the straight line are one and the same”. Points and straight lines are Published: October 30, 2020 not treated as dual elements in two separate sets, but identical elements with- in a single set endowed with a binary operation and appropriate axioms. It Copyright © 2020 by author(s) and consists of three sections. In Section 1 I build an algebraic system based on Scientific Research Publishing Inc. This work is licensed under the Creative spherical constructions with two axioms: ab= ba and (ab)( ac) = a , pro- Commons Attribution International viding finite and infinite models and proving classical theorems that are License (CC BY 4.0). adapted to the new system. In Section Two I arrange hyperbolic points and http://creativecommons.org/licenses/by/4.0/ straight lines into a model of a projective sphere, show the connection be- Open Access tween the spherical Napier pentagram and the hyperbolic Napier pentagon, and describe new synthetic and trigonometric findings between spherical and hyperbolic geometry.
    [Show full text]
  • Strophoids, a Family of Cubic Curves with Remarkable Properties
    Hellmuth STACHEL STROPHOIDS, A FAMILY OF CUBIC CURVES WITH REMARKABLE PROPERTIES Abstract: Strophoids are circular cubic curves which have a node with orthogonal tangents. These rational curves are characterized by a series or properties, and they show up as locus of points at various geometric problems in the Euclidean plane: Strophoids are pedal curves of parabolas if the corresponding pole lies on the parabola’s directrix, and they are inverse to equilateral hyperbolas. Strophoids are focal curves of particular pencils of conics. Moreover, the locus of points where tangents through a given point contact the conics of a confocal family is a strophoid. In descriptive geometry, strophoids appear as perspective views of particular curves of intersection, e.g., of Viviani’s curve. Bricard’s flexible octahedra of type 3 admit two flat poses; and here, after fixing two opposite vertices, strophoids are the locus for the four remaining vertices. In plane kinematics they are the circle-point curves, i.e., the locus of points whose trajectories have instantaneously a stationary curvature. Moreover, they are projections of the spherical and hyperbolic analogues. For any given triangle ABC, the equicevian cubics are strophoids, i.e., the locus of points for which two of the three cevians have the same lengths. On each strophoid there is a symmetric relation of points, so-called ‘associated’ points, with a series of properties: The lines connecting associated points P and P’ are tangent of the negative pedal curve. Tangents at associated points intersect at a point which again lies on the cubic. For all pairs (P, P’) of associated points, the midpoints lie on a line through the node N.
    [Show full text]