DOCSLIB.ORG

M.S. Physics and Astronomy, University of Pittsburgh, 2005

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
M.S. Physics and Astronomy, University of Pittsburgh, 2005 REFLECTION ON PROBLEM SOLVING IN INTRODUCTORY AND ADVANCED PHYSICS by Andrew J. Mason B.S. Physics, State University of New York at Buffalo, 2004 M.S. Physics and Astronomy, University of Pittsburgh, 2005 Submitted to the Graduate Faculty of the Department of Physics and Astronomy in partial fulfillment of the requirements for the degree of Doctor of Philosophy University of Pittsburgh 2009 UNIVERSITY OF PITTSBURGH SCHOOL OF ARTS AND SCIENCES DEPARTMENT OF PHYSICS AND ASTRONOMY This dissertation was presented by Andrew J. Mason It was defended on July 7, 2009 and approved by Dissertation Advisor: Dr. Chandralekha Singh, Associate Professor, Department of Physics and Astronomy Dr. Peter F. M. Koehler, Professor, Department of Physics and Astronomy Dr. Adam Leibovich, Associate Professor, Department of Physics and Astronomy Dr. Robert P. Devaty, Associate Professor, Department of Physics and Astronomy Dr. Christian Schunn, Associate Professor, Department of Psychology ii Copyright © by Andrew J. Mason 2009 iii REFLECTION ON PROBLEM SOLVING IN INTRODUCTORY AND ADVANCED PHYSICS Andrew J. Mason, PhD University of Pittsburgh, 2009 Reflection is essential in order to learn from problem solving. This thesis explores issues related to how reflective students are and how we can improve their capacity for reflection on problem solving. We investigate how students naturally reflect in their physics courses about problem solving and evaluate strategies that may teach them reflection as an integral component of problem-solving. Problem categorization based upon similarity of solution is a strategy to help them reflect about the deep features of the problems related to the physics principles involved. We find that there is a large overlap between the introductory and graduate students in their ability to categorize. Moreover, introductory students in the calculus-based courses performed better categorization than those in the algebra-based courses even though the categorization task is conceptual. Other investigations involved exploring if reflection could be taught as a skill on individual and group levels. Explicit self-diagnosis in recitation investigated how effectively students could diagnose their own errors on difficult problems, how much scaffolding was necessary for this purpose, and how effective transfer was to other problems employing similar principles. Difficulty in applying physical principles and difference between the self-diagnosed and transfer problems affected performance. We concluded that a sustained intervention is required to learn effective problem-solving strategies. Another study involving reflection on problem solving with peers suggests that those who reflected with peers drew more diagrams and had a larger gain from the midterm to final exam. Another study in quantum mechanics involved iv giving common problems in midterm and final exams and suggested that advanced students do not automatically reflect on their mistakes. Interviews revealed that even advanced students often focus mostly on exams rather than learning and building a robust knowledge structure. A survey was developed to further evaluate students’ attitudes and approaches towards problem solving. The survey responses suggest that introductory students and even graduate students have different attitudes and approaches to problem solving on several important measures compared to physics faculty members. Furthermore, responses to individual survey questions suggest that expert and novice attitudes and approaches to problem solving may be more complex than naively considered. v TABLE OF CONTENTS PREFACE - ACKNOWLEDGMENTS ............................................................................... XXII 1.0 INTRODUCTION ........................................................................................................ 1 1.1 PROBLEM SOLVING: DEFINITION ............................................................. 2 1.2 INFLUENCE FROM COGNITIVE SCIENCE: THE CONCEPT OF MEMORY ............................................................................................................................. 3 1.2.1 Schemata........................................................................................................... 4 1.2.2 Chunking and Cognitive Load during Problem Solving ............................. 4 1.3 METACOGNITION ............................................................................................ 7 1.3.1 Metacognition, heuristics, and the problem-solving process ....................... 7 1.4 PHYSICIST’S PERSPECTIVE: AN OVERVIEW OF PROBLEM SOLVING IN PER ............................................................................................................... 9 1.5 REFLECTION ON PROBLEM SOLVING ................................................... 13 1.5.1 The Cognitive Apprenticeship Model .......................................................... 14 1.6 A STUDY OF REFLECTION IN THE CONTEXT OF PROBLEM SOLVING ............................................................................................................................ 16 1.7 CHAPTER REFERENCES .............................................................................. 18 2.0 CATEGORIZATION REVISITED: ASSESSING STUDENT ENTERPRISE IN INTRODUCTORY PHYSICS ................................................................................................... 25 vi 2.1 ABSTRACT ........................................................................................................ 25 2.2 INTRODUCTION ............................................................................................. 26 2.2.1 Goals and Motivation .................................................................................... 27 2.3 CATEGORIZATION TASK AND DETERMINATION OF GOOD CATEGORIES ................................................................................................................... 28 2.4 RESULTS ........................................................................................................... 35 2.4.1 Dependence of Categorization on the Nature of Problems ........................ 36 2.4.2 Comparison between the Algebra-Based and Calculus-Based Introductory Physics Classes .................................................................................... 40 2.4.3 Comparison of Calculus-Based Introductory Students with Physics Graduate Students ..................................................................................................... 51 2.4.4 Correlation between Categorization and Course Grade ........................... 56 2.4.5 Interviews with Individual Students ............................................................ 56 2.5 SUMMARY AND CONCLUSIONS ................................................................ 63 2.6 ACKNOWLEDGMENTS ................................................................................. 67 2.7 REFERENCES .................................................................................................. 67 3.0 SELF-DIAGNOSIS IN INTRODUCTORY PHYSICS .......................................... 70 3.1 ABSTRACT ........................................................................................................ 70 3.2 STUDY 1: SELF-DIAGNOSIS AND TRANSFER FOR AN ATYPICAL QUIZ 71 3.2.1 Introduction ................................................................................................... 71 3.2.2 Rationale for Self-Diagnosis Tasks .............................................................. 74 3.2.3 Experimental Setup ....................................................................................... 79 vii 3.2.3.1 Sample .................................................................................................. 79 3.2.3.2 Interventions and Control .................................................................. 80 3.2.4 Analysis Tools ................................................................................................ 81 3.2.4.1 Structure of the rubric ........................................................................ 81 3.2.4.2 Scoring rubric for quiz 6 .................................................................... 84 3.2.5 Results ............................................................................................................. 88 3.2.5.1 Self-diagnosis - Physics ....................................................................... 88 3.2.5.2 Self-diagnosis - Presentation .............................................................. 90 3.2.5.3 Self-diagnosis and Prior Knowledge ................................................. 93 3.2.6 The Midterm Problem................................................................................... 94 3.2.6.1 Midterm Physics Scores ...................................................................... 95 3.2.6.2 Physics Self-Diagnosis vs. Midterm Performance ............................ 98 3.2.6.3 Midterm Presentation Scores ............................................................. 98 3.3 PART 2 OF THE STUDY: A MORE CONVENTIONAL QUIZ PROBLEM 100 3.3.1 Introduction ................................................................................................. 100 3.3.2 Sample Problem: Quiz Problem Used for Self-Diagnosis ........................ 102 3.3.3 The Rubric Adapted .................................................................................... 103 3.3.3.1 Specific Knowledge: Categories and Subcategories ...................... 103 3.3.3.2 Scoring ...............................................................................................
Load more

Recommended publications
  • 2005 Annual Report American Physical Society
    1 2005 Annual Report American Physical Society APS 20052 APS OFFICERS 2006 APS OFFICERS PRESIDENT: PRESIDENT: Marvin L. Cohen John J. Hopfield University of California, Berkeley Princeton University PRESIDENT ELECT: PRESIDENT ELECT: John N. Bahcall Leo P. Kadanoff Institue for Advanced Study, Princeton University of Chicago VICE PRESIDENT: VICE PRESIDENT: John J. Hopfield Arthur Bienenstock Princeton University Stanford University PAST PRESIDENT: PAST PRESIDENT: Helen R. Quinn Marvin L. Cohen Stanford University, (SLAC) University of California, Berkeley EXECUTIVE OFFICER: EXECUTIVE OFFICER: Judy R. Franz Judy R. Franz University of Alabama, Huntsville University of Alabama, Huntsville TREASURER: TREASURER: Thomas McIlrath Thomas McIlrath University of Maryland (Emeritus) University of Maryland (Emeritus) EDITOR-IN-CHIEF: EDITOR-IN-CHIEF: Martin Blume Martin Blume Brookhaven National Laboratory (Emeritus) Brookhaven National Laboratory (Emeritus) PHOTO CREDITS: Cover (l-r): 1Diffraction patterns of a GaN quantum dot particle—UCLA; Spring-8/Riken, Japan; Stanford Synchrotron Radiation Lab, SLAC & UC Davis, Phys. Rev. Lett. 95 085503 (2005) 2TESLA 9-cell 1.3 GHz SRF cavities from ACCEL Corp. in Germany for ILC. (Courtesy Fermilab Visual Media Service 3G0 detector studying strange quarks in the proton—Jefferson Lab 4Sections of a resistive magnet (Florida-Bitter magnet) from NHMFL at Talahassee LETTER FROM THE PRESIDENT APS IN 2005 3 2005 was a very special year for the physics community and the American Physical Society. Declared the World Year of Physics by the United Nations, the year provided a unique opportunity for the international physics community to reach out to the general public while celebrating the centennial of Einstein’s “miraculous year.” The year started with an international Launching Conference in Paris, France that brought together more than 500 students from around the world to interact with leading physicists.
    [Show full text]
  • Student Study Guide for Fundamentals of Physics, 10E David Halliday, Robert Resnick, Jearl Walker, Thomas E
    To purchase this product, please visit https://www.wiley.com/en-us/9781119420569 Student Study Guide for Fundamentals of Physics, 10e David Halliday, Robert Resnick, Jearl Walker, Thomas E. Barrett E-Book Rental (120 Days) 978-1-119-42056-9 April 2017 $16.00 E-Book Rental (150 Days) 978-1-119-42056-9 April 2017 $19.00 E-Book 978-1-119-42056-9 April 2017 $47.50 DESCRIPTION This is the Student Study Guide to accompany Fundamentals of Physics, 10th Edition. The 10 th edition of Halliday's Fundamentals of Physics, builds upon previous issues by offering several new features and additions. The new edition offers most accurate, extensive and varied set of assessment questions of any course management program in addition to all questions including some form of question assistance including answer specific feedback to facilitate success. The text also offers multimedia presentations (videos and animations) of much of the material that provide an alternative pathway through the material for those who struggle with reading scientific exposition. Furthermore, the book includes math review content in both a self-study module for more in-depth review and also in just-in-time math videos for a quick refresher on a specific topic. The Halliday content is widely accepted as clear, correct, and complete. The end-of-chapters problems are without peer. The new design, which was introduced in 9e continues with 10e, making this new edition of Halliday the most accessible and reader- friendly book on the market. ABOUT THE AUTHOR David Halliday is associated with the University of Pittsburgh as Professor Emeritus.
    [Show full text]
  • You Should Take the Lab Phys 221 Along with This Course If You Have Not Already Passed It
    Course Outline Course: Physics for Science and Engineering I Instructor: Dr Alakabha Datta Office: 121-B Lewis Hall Meeting: Tues 11 am- 12.15 pm at Lewis 101 Thurs 11 am-12.15 pm at Lewis 101 Office Hours: Tues and Thursdays 10am-10.50 am or by appointment. Email:[email protected], [email protected] Phone: (662) 915-5611 Course Information: check Blackboard. NOTE: You should take the Lab Phys 221 along with this course if you have not already passed it. Book Fundamentals of Physics, 7th Edition David Halliday, Univ. of Pittsburgh Robert Resnick, Rensselaer Polytechnic Institute Jearl Walker, Cleveland State Univ. ISBN: 0-471-21643-7 ©2005 1136 pages Student Site: http://bcs.wiley.com/he-bcs/Books?action=index&bcsId=2037&itemId=0471216437 Course Goals: Learning the basic laws of physics concerning particle motion and wave phenomena and its application to various engineering sciences and to everyday life. You will also learn to analyze problems logically and systematically. Marking: Homework: 40 % Homework: I will assign weekly homework that has to be turned in one week. No late homework will be accepted after the due date. Please write your name in block letters and include the problem set number with your homework. You can get help to do your homework but turn in your own work. Do not copy some from someone. There is a tutoring room available for help with your homework. Homework solutions will be emailed to all students and will be posted on Blackboard. Tests: 30% There will be 3 tests each worth 10% and will roughly given at intervals of a month.
    [Show full text]
  • Fundamentals of Physics, 10Th Edition David Halliday, Robert Resnick, Jearl Walker
    To purchase this product, please visit https://www.wiley.com/en-us/9781119040231 Fundamentals of Physics, 10th Edition David Halliday, Robert Resnick, Jearl Walker E-Book Rental (120 Days) 978-1-119-04023-1 January 2015 $39.00 E-Book Rental (150 Days) 978-1-119-04023-1 January 2015 $45.00 E-Book 978-1-119-04023-1 January 2015 $112.50 Loose-leaf 978-1-118-23064-0 August 2013 $124.95 Hardcover 978-1-118-23071-8 August 2013 $299.95 DESCRIPTION The 10 th edition of Halliday, Resnick and Walkers Fundamentals of Physics provides the perfect solution for teaching a 2 or 3 semester calculus-based physics course, providing instructors with a tool by which they can teach students how to effectively read scientific material, identify fundamental concepts, reason through scientific questions, and solve quantitative problems. The 10th edition builds upon previous editions by offering new features designed to better engage students and support critical thinking. These include NEW Video Illustrations that bring the subject matter to life, NEW Vector Drawing Questions that test students conceptual understanding, and additional multimedia resources (videos and animations) that provide an alternative pathway through the material for those who struggle with reading scientific exposition. WileyPLUS sold separately from text. ABOUT THE AUTHOR David Halliday is associated with the University of Pittsburgh as Professor Emeritus. As department chair in 1960, he and Robert Resnick collaborated on Physics for Students of Science and Engineering and then on Fundamentals of Physics. Fundamentals is currently in its eighth edition and has since been handed over from Halliday and Resnick to Jearl Walker.
    [Show full text]
  • History Newsletter CENTER for HISTORY of PHYSICS&NIELS BOHR LIBRARY & ARCHIVES Vol
    History Newsletter CENTER FOR HISTORY OF PHYSICS&NIELS BOHR LIBRARY & ARCHIVES Vol. 41, No. 2 • Fall 2009 Digitizing the Samuel Goudsmit Papers In the Fall 2008 issue of the Newsletter other fasteners. Where necessary they for each image, resulting in a more read- we reported that the Library & Archives replaced the fasteners with strips of able digital representation. had received a grant from the National acid-free paper, and they flattened Historical Publications and Records folded edges and crumpled corners. As the vendor returns the scanned doc- Commission (NHPRC) to scan and uments, the next and most important mount online the complete papers of The prepared documents are being phase of the project begins—review Samuel A. Goudsmit, consisting of an transported in small batches to Macfad- of each page. Melanie and Rebecca estimated 66,000 individual items. den & Associates in nearby Silver Spring, compare each scanned image with its original document, We promised that we’d verifying that the cor- keep you updated, and rect image has been we’re pleased to report scanned, the image is that the entire collection oriented properly, and has been prepared for the contrast is light or shipment to the imag- dark enough to read ing vendor, Macfadden penciled annotations & Associates; the first 12 and fading carbon boxes of the collection sheets. If an image have been scanned; and does not meet these staff are beginning to and other archival review the scanned im- specifications, it’s re- ages. turned to the vendor to be rescanned. Creating an archival- quality digital facsimile With the help of of the Goudsmit Papers requires MD.
    [Show full text]
  • 2012 Report Executive Board President Jill A
    American Association of Physics Teachers annual2012 report Executive Board President Jill A. Marshall University of Texas – Austin Austin, TX President-Elect Gay Stewart University of Arkansas Fayetteville, AR Vice President Mary Beth Monroe Southwest Texas Junior College Uvalde, TX 2012 Secretary in Summary Steven Iona University of Colorado Denver, CO Treasurer Paul W. Zitzewitz University of Michigan – Dearborn Dearborn, MI Past President Presidential Statement 3 David R. Sokoloff Executive Officer Statement 4 University of Oregon Strategic Plan 6 Eugene, OR Publications 7 Chair of Section Representatives Marina Milner-Bolotin Electronic Communications 9 The University of British Columbia Membership 11 Vancouver, BC National Meetings 12 Vice Chair of Section Representatives Gregory Puskar Workshops and Programs 16 West Virginia University Collaborative Projects 19 Morgantown, WV Awards and Grants 22 At-Large Board Members Paul Williams Fundraising 27 Austin Community College Committee Contributions 29 Austin, TX AAPT Sections 31 Diane M. Riendeau Deerfield High School Financials 32 Deerfield, IL Steve Shropshire Idaho State University Pocatello, ID Editor American Journal of Physics David P. Jackson Dickinson College Carlisle, PA Editor The Physics Teacher Karl C. Mamola Appalachian State University Boone, NC Executive Officer Beth A. Cunningham President – Jill Marshall AAPT is a great organization to be part of—and the endowment. I am pleased to say that 2013 right now we are moving in exciting directions. will see a major campaign to fund the Phillips 2012 saw our finances continuing on the Medal. sound heading set in 2011 by my predecessor Recruiting and maintaining members con- David Sokoloff, Executive Officer Beth -Cun tinued to be a challenge in 2012, particularly ningham, and the Senior Management Team.
    [Show full text]
  • S U B S T a N C E Abljsf
    SUBSTANCE ABLJSF Volume 26, Number 1 Division 28 - The American Psychological Association Spring, 1993 PRESIDENT'S LETTER group of psychologists and affords the opportunity to learn about recent developments in many allied areas, including Maxine Stitzer experimental analysis of behavior, mental retardation, aging, President, Division 28 and health psychology. Finally, the annual convention is an important forum for sciencelpractice interchange in the Division 28 has sustained a steady membership level of mental health and substance abuse treatment arenas. about 1,000 individuals over the years from 1970 to 1990. This has allowed us to participate effectively in the informa- Science advocacy is another major reason to belong to tion exchange and advocacy programs of APA. The total APA Division 28. The APA Science and Public Policy APA membership is growing, however, and we need to keep directorates work together to keep legislators aware of cur- up with the times. As a current member, you know about rent issues and the importance of scientific input to public the numerous benefits of membership, including this quarter- policy questions. Our members have been active in formulat- ly newsletter that keeps you updated on Division activities. ing policies for adequate care of research animals and in We are asking for your help in attracting new members. promoting public awareness of the utility and benefits of animal research. Neurobehavioral toxicology is a strong Who should join? interest of some Division members who have participated in
    [Show full text]
  • [New] Name? CENTER
    CENTER FOR HISTORY OF PHYSICS NEWSLETTER Vol. XXXIX, Number 1 Spring 2007 One Physics Ellipse, College Park, MD 20740-3843, Tel. 301-209-3165 Publication of the Collected Works of Niels Bohr Completed by Finn Aaserud ith the publication of the twelfth and final volume of the W Niels Bohr Collected Works, one of the very greatest physicists of the twentieth century is brought before the public in one of the premier works of scholarship in modern history of science. Planning for the publication of the Collected Works began soon after Bohr’s death in 1962. The driving force behind the project was Bohr’s close collaborator, the Belgian physicist and historian of science Léon Rosenfeld, who was the first General Editor of the series. The first volume, covering the early years up to 1911, was published in 1972 with Jens Rud Nielsen (1894–1979) as editor. However, this was the only volume that Rosenfeld would see, for he died in 1974. The project, originally conceived as a ten-year effort, was not completed until well into the next century. After an interim period with Rud Nielsen doing the brunt of the work, Erik Rüdinger was named General Editor in 1977. Mary Calvert using the 12-inch refractor at Yerkes Observatory, Rüdinger had served as Bohr’s scientific assistant for a brief February 23, 1926. She was Edward E. Barnard’s niece, and after period near the end of Bohr’s life. In Volume 5 (published his death, co-editor of his book A Photographic Atlas of Selected 1985), the first under Rüdinger’s control, Rüdinger laid out the Regions of the Milky Way published in 1927 by the Carnegie general editorial policy and practice that have been followed Institution of Washington.
    [Show full text]
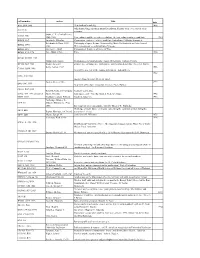
  • Call Number Author Title Date AG5 .B64 2006 New Book of Knowledge
    call number author Title date AG5 .B64 2006 New book of knowledge. 2006 John Simon Guggenheim memorial foundation. Reports of the secretary & of the AS911.J6 treasurer. Snow, C. P. (Charles Percy), AZ361 .S56 1905-1980 Two cultures and the scientific revolution, the two cultures and a second look 1963 BD632 .F67 Formánek, Miloslav. Časoprostor v politice : některé problémy fyzikalismu / Miloslav Formánek. Reichenbach, Hans, 1891- Philosophy of space & time. Translated by Maria Reichenbach and John Freund. BD632 .R413 1953. With introductory remarks by Rudolf Carnap. BD632.G92 Gurnbaum, Adolf Philosophical Problems of Space of Time BD638 .P73 1996 Price, Huw, 1953- Price. 1996 BH301.N3 H55 1985 Hildebrandt, Stefan. Mathematics and optimal form / Stefan Hildebrandt, Anthony Tromba. BT130 .B69 1983 Brams, Steven J. omniscience, omnipotence, immortality, and incomprehensibility / Steven J. Brams. Berry, Adrian, 1937- 1996 CB161 .B459 1996 Next 500 years : life in the coming millennium / Adrian Berry. 1982 E158 .A48 1982 America from the road / Reader's digest. Forbes, Steve, 1947- 1999 E885 .F67 1999 New birth of freedom : vision for America / Steve Forbes. G1019 .R47 1955 Rand McNally and Company. Standard world atlas. G70.4 .S77 1992 oversized Strain, Priscilla. Looking at earth / Priscilla Strain & Frederick Engle. 1992 GB55 .G313 Gaddum, Leonard William, Harold L. Knowles. 1953 Fairbridge, Rhodes W. GC9 .F3 (Rhodes Whitmore), 1914- 2006. Encyclopedia of oceanography, edited by Rhodes W. Fairbridge. Challenge of man's future; an inquiry concerning the condition of man during the GF31 .B68 Brown, Harrison, 1917-1986. years that lie ahead. GF47 .M63 Moran, Joseph M. [and] James H. Wiersma. 1973 Anderson, Walt, 1933- 1996 GN281.4 .A53 1996 Evolution isn't what it used to be : the augmented animal and the whole wired world / Walter Truett Anderson.
    [Show full text]
  • Penn Dental Journal
    Penn Dental Journal For the University of Pennsylvania School of Dental Medicine Community / Fall 2012 Growing a World-Class Faculty: Three New Recruits Bring Depth of Clinical, Research Expertise | page 2 Faculty Perspective: Oral Cancer Screening | page 7 | Facilities Update, Master Plan Spotlight | page 8 Answering the Call to Higher Education: Alumni in Academia | page 10 Honor Roll: 2011 –12 Donors | page 29 in this issue Features 2 Growing a World-Class Faculty Penn Dental Journal by katherine unger baillie Vol. 9, No. 1 7 Faculty Perspective: University of Pennsylvania Oral Cancer Screening School of Dental Medicine www.dental.upenn.edu by faizan alawi, dds Dean denis f. kinane, bds, phd 8 Facilities Update, TWO THUMBS UP! NEW ENDODONTIC CLINIC Master Plan Spotlight ON TRACK FOR EARLY 2013 OPENING, Associate Dean for Development PAGE 8. and Alumni Relations by beth adams maren gaughan Director, Publications 10 Answering the Call to beth adams Higher Education Contributing Writers by juliana delany Departments beth adams katherine unger baillie juliana delany 17 On Campus: News and People debbie goldberg 25 Scholarly Activity Design 28 Philanthropy Highlights dyad communications 29 Philanthropy Honor Roll Photography mark garvin 37 Alumni: News peter olson 41 Class Notes Penn Dental Journal is published twice a year for the alumni and friends of the 44 In Memoriam University of Pennsylvania School of Dental Medicine. ©2012 by the Trustees of the University of Pennsylvania. All rights reserved. We would like to get your feed - ALUMNI WEEKEND 2012 WELCOMED REUNION back and input on the Penn Dental Journal CLASSES ENDING IN “2” AND “7”, PAGE 38.
    [Show full text]
  • Fundamentals of Physics Extended, 10Th Edition
    To purchase this product, please visit https://www.wiley.com/en-us/9781118230725 Fundamentals of Physics, Extended, 10th Edition David Halliday, Robert Resnick, Jearl Walker E-Book Rental (120 Days) 978-1-118-54787-8 March 2013 $39.00 E-Book Rental (150 Days) 978-1-118-54787-8 March 2013 $45.00 E-Book 978-1-118-54787-8 March 2013 $112.50 Loose-leaf 978-1-118-23061-9 August 2013 $124.95 Hardcover 978-1-118-23072-5 August 2013 $310.95 DESCRIPTION The 10 th edition of Halliday's Fundamentals of Physics, Extended building upon previous issues by offering several new features and additions. The new edition offers most accurate, extensive and varied set of assessment questions of any course management program in addition to all questions including some form of question assistance including answer specific feedback to facilitate success. The text also offers multimedia presentations (videos and animations) of much of the material that provide an alternative pathway through the material for those who struggle with reading scientific exposition. Furthermore, the book includes math review content in both a self-study module for more in-depth review and also in just-in-time math videos for a quick refresher on a specific topic. The Halliday content is widely accepted as clear, correct, and complete. The end-of-chapters problems are without peer. The new design, which was introduced in 9e continues with 10e, making this new edition of Halliday the most accessible and reader- friendly book on the market. WileyPLUS sold separately from text. ABOUT THE AUTHOR David Halliday was an American physicist known for his physics textbooks, Physics and Fundamentals of Physics, which he wrote with Robert Resnick.
    [Show full text]
  • You Should Take the Lab Phys 222 Along with This Course If You Have Not Already Passed It
    Course Outline Course: Physics for Science and Engineering II Instructor: Dr Alakabha Datta Office: 121-B Lewis Hall Meeting: Tues 11 am- 12.15 pm at Lewis 101 Thurs 11 am-12.15 pm at Lewis 101 Office Hours: Tues and Thursdays 10am-10.50 am or by appointment. Email:[email protected], [email protected] Phone: (662) 915-5611 Course homepage: http://www.phy.olemiss.edu/~datta/212.html Also check Blackboard. NOTE: You should take the Lab Phys 222 along with this course if you have not already passed it. Book Fundamentals of Physics, 7th Edition David Halliday, Univ. of Pittsburgh Robert Resnick, Rensselaer Polytechnic Institute Jearl Walker, Cleveland State Univ. ISBN: 0-471-21643-7 ©2005 1136 pages Student Site: http://bcs.wiley.com/he-bcs/Books?action=index&bcsId=2037&itemId=0471216437 Course Goals: Learning basic laws of physics concerning electromagnetic phenomena and its application to various engineering sciences and to everyday life. You will also learn to analyze problems logically and systematically. Marking: Homework 30% Homework: I will assign weekly homework that has to be turned in one week. There is a 25% penalty for late HW submission. No homework will be accepted three days after the due date. Please write your name in block letters and include the problem set number with your homework. Midterm Exam: 25% Midterm will be given over two classes. Dates will be announced later. Final Exam: 45% Wed Dec 6, 2006 at noon (See Class Schedule) An overall course average of the following percentages will guarantee the corresponding letter grade: 90% A 80% B 70% C 60% D _____________________________________________________________ Topics Covered in course: Topics will be taken from the following chapter.
    [Show full text]