Intensity Spots in the Cosmic Microwave Background Radiation and Distant Objects V
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Large-Scale Outflows in Edge-On Seyfert Galaxies. II. Kiloparsec
Large-Scale Outflows in Edge-on Seyfert Galaxies. II. Kiloparsec-Scale Radio Continuum Emission Edward J. M. Colbert1,2, Stefi A. Baum1, Jack F. Gallimore1,2, Christopher P. O’Dea1, Jennifer A. Christensen1 Received ; accepted arXiv:astro-ph/9604022v1 3 Apr 1996 1 Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218 2 Department of Astronomy, University of Maryland, College Park, MD 20742 –2– ABSTRACT We present deep images of the kpc-scale radio continuum emission in 14 edge-on galaxies (ten Seyfert and four starburst galaxies). Observations were taken with the VLA at 4.9 GHz (6 cm). The Seyfert galaxies were selected from a distance-limited sample of 22 objects (defined in paper I). The starburst galaxies were selected to be well-matched to the Seyferts in radio power, recessional velocity and inclination angle. All four starburst galaxies have a very bright disk component and one (NGC 3044) has a radio halo that extends several kpc out of the galaxy plane. Six of the ten Seyferts observed have large-scale (radial extent >1 kpc) radio structures extending outward from the ∼ nuclear region, indicating that large-scale outflows are quite common in Seyferts. Large-scale radio sources in Seyferts are similar in radio power and radial extent to radio halos in edge-on starburst galaxies, but their morphologies do not resemble spherical halos observed in starburst galaxies. The sources have diffuse morphologies, but, in general, they are oriented at skewed angles with respect to the galaxy minor axes. This result is most easily understood if the outflows are AGN-driven jets that are somehow diverted away from the galaxy disk on scales >1 kpc. -

Making a Sky Atlas
Appendix A Making a Sky Atlas Although a number of very advanced sky atlases are now available in print, none is likely to be ideal for any given task. Published atlases will probably have too few or too many guide stars, too few or too many deep-sky objects plotted in them, wrong- size charts, etc. I found that with MegaStar I could design and make, specifically for my survey, a “just right” personalized atlas. My atlas consists of 108 charts, each about twenty square degrees in size, with guide stars down to magnitude 8.9. I used only the northernmost 78 charts, since I observed the sky only down to –35°. On the charts I plotted only the objects I wanted to observe. In addition I made enlargements of small, overcrowded areas (“quad charts”) as well as separate large-scale charts for the Virgo Galaxy Cluster, the latter with guide stars down to magnitude 11.4. I put the charts in plastic sheet protectors in a three-ring binder, taking them out and plac- ing them on my telescope mount’s clipboard as needed. To find an object I would use the 35 mm finder (except in the Virgo Cluster, where I used the 60 mm as the finder) to point the ensemble of telescopes at the indicated spot among the guide stars. If the object was not seen in the 35 mm, as it usually was not, I would then look in the larger telescopes. If the object was not immediately visible even in the primary telescope – a not uncommon occur- rence due to inexact initial pointing – I would then scan around for it. -

Ngc Catalogue Ngc Catalogue
NGC CATALOGUE NGC CATALOGUE 1 NGC CATALOGUE Object # Common Name Type Constellation Magnitude RA Dec NGC 1 - Galaxy Pegasus 12.9 00:07:16 27:42:32 NGC 2 - Galaxy Pegasus 14.2 00:07:17 27:40:43 NGC 3 - Galaxy Pisces 13.3 00:07:17 08:18:05 NGC 4 - Galaxy Pisces 15.8 00:07:24 08:22:26 NGC 5 - Galaxy Andromeda 13.3 00:07:49 35:21:46 NGC 6 NGC 20 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 7 - Galaxy Sculptor 13.9 00:08:21 -29:54:59 NGC 8 - Double Star Pegasus - 00:08:45 23:50:19 NGC 9 - Galaxy Pegasus 13.5 00:08:54 23:49:04 NGC 10 - Galaxy Sculptor 12.5 00:08:34 -33:51:28 NGC 11 - Galaxy Andromeda 13.7 00:08:42 37:26:53 NGC 12 - Galaxy Pisces 13.1 00:08:45 04:36:44 NGC 13 - Galaxy Andromeda 13.2 00:08:48 33:25:59 NGC 14 - Galaxy Pegasus 12.1 00:08:46 15:48:57 NGC 15 - Galaxy Pegasus 13.8 00:09:02 21:37:30 NGC 16 - Galaxy Pegasus 12.0 00:09:04 27:43:48 NGC 17 NGC 34 Galaxy Cetus 14.4 00:11:07 -12:06:28 NGC 18 - Double Star Pegasus - 00:09:23 27:43:56 NGC 19 - Galaxy Andromeda 13.3 00:10:41 32:58:58 NGC 20 See NGC 6 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 21 NGC 29 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 22 - Galaxy Pegasus 13.6 00:09:48 27:49:58 NGC 23 - Galaxy Pegasus 12.0 00:09:53 25:55:26 NGC 24 - Galaxy Sculptor 11.6 00:09:56 -24:57:52 NGC 25 - Galaxy Phoenix 13.0 00:09:59 -57:01:13 NGC 26 - Galaxy Pegasus 12.9 00:10:26 25:49:56 NGC 27 - Galaxy Andromeda 13.5 00:10:33 28:59:49 NGC 28 - Galaxy Phoenix 13.8 00:10:25 -56:59:20 NGC 29 See NGC 21 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 30 - Double Star Pegasus - 00:10:51 21:58:39 -

Arp Catalogue.Xlsx
ATLAS OF PECULIAR GALAXIES CATALOGUE 1 ATLAS OF PECULIAR GALAXIES CATALOGUE Object Name Mag RA Dec Constellation ARP 1 NGC 2857 12.2 09:24:37 49:21:00 Ursa Major ARP 2 13.2 16:16:18 47:02:00 Hercules ARP 3 13.4 22:36:34 ‐02:54:00 Aquarius ARP 4 13.7 01:48:25 ‐12:22:00 Cetus ARP 5 NGC 3664 12.8 11:24:24 03:19:00 Leo ARP 6 NGC 2537 12.3 08:13:14 45:59:00 Lynx ARP 7 14.5 08:50:17 ‐16:34:00 Hydra ARP 8 NGC 0497 13 01:22:23 ‐00:52:00 Cetus ARP 9 NGC 2523 11.9 08:14:59 73:34:00 Camelopardalis ARP 10 13.8 02:18:26 05:39:00 Cetus ARP 11 14.4 01:09:23 14:20:00 Pisces ARP 12 NGC 2608 12.2 08:35:17 28:28:00 Cancer ARP 13 NGC 7448 11.6 23:00:02 15:59:00 Pegasus ARP 14 NGC 7314 10.9 22:35:45 ‐26:03:00 Pisces Austrinus ARP 15 NGC 7393 12.6 22:51:39 ‐05:33:00 Aquarius ARP 16 M66 8.9 11:20:14 12:59:00 Leo ARP 17 14.7 07:44:32 73:49:00 Camelopardalis ARP 17 07:44:38 73:48:00 Camelopardalis ARP 18 NGC 4088 10.5 12:05:35 50:32:00 Ursa Major ARP 19 NGC 0145 13.2 00:31:45 ‐05:09:00 Cetus ARP 20 14.4 04:19:53 02:05:00 Taurus ARP 21 14.7 11:04:58 30:01:00 Leo Minor ARP 22 14.9 11:59:29 ‐19:19:00 Corvus ARP 22 NGC 4027 11.2 11:59:30 ‐19:15:00 Corvus ARP 23 NGC 4618 10.8 12:41:32 41:09:00 Canes Venatici ARP 24 NGC 3445 12.6 10:54:36 56:59:00 Ursa Major ARP 24 12.8 10:54:45 56:57:00 Ursa Major ARP 25 NGC 2276 11.4 07:27:13 85:45:00 Cepheus ARP 26 M101 7.9 14:03:12 54:21:00 Ursa Major ARP 27 NGC 3631 10.4 11:21:02 53:10:00 Ursa Major ARP 28 NGC 7678 11.8 23:28:27 22:25:00 Pegasus ARP 29 NGC 6946 8.8 20:34:52 60:09:00 Cygnus ARP 30 NGC 6365 12.2 17:22:42 62:10:00 -

Atlante Grafico Delle Galassie
ASTRONOMIA Il mondo delle galassie, da Kant a skylive.it. LA RIVISTA DELL’UNIONE ASTROFILI ITALIANI Questo è un numero speciale. Viene qui presentato, in edizione ampliata, quan- [email protected] to fu pubblicato per opera degli Autori nove anni fa, ma in modo frammentario n. 1 gennaio - febbraio 2007 e comunque oggigiorno di assai difficile reperimento. Praticamente tutte le galassie fino alla 13ª magnitudine trovano posto in questo atlante di più di Proprietà ed editore Unione Astrofili Italiani 1400 oggetti. La lettura dell’Atlante delle Galassie deve essere fatto nella sua Direttore responsabile prospettiva storica. Nella lunga introduzione del Prof. Vincenzo Croce il testo Franco Foresta Martin Comitato di redazione e le fotografie rimandano a 200 anni di studio e di osservazione del mondo Consiglio Direttivo UAI delle galassie. In queste pagine si ripercorre il lungo e paziente cammino ini- Coordinatore Editoriale ziato con i modelli di Herschel fino ad arrivare a quelli di Shapley della Via Giorgio Bianciardi Lattea, con l’apertura al mondo multiforme delle altre galassie, iconografate Impaginazione e stampa dai disegni di Lassell fino ad arrivare alle fotografie ottenute dai colossi della Impaginazione Grafica SMAA srl - Stampa Tipolitografia Editoria DBS s.n.c., 32030 metà del ‘900, Mount Wilson e Palomar. Vecchie fotografie in bianco e nero Rasai di Seren del Grappa (BL) che permettono al lettore di ripercorrere l’alba della conoscenza di questo Servizio arretrati primo abbozzo di un Universo sempre più sconfinato e composito. Al mondo Una copia Euro 5.00 professionale si associò quanto prima il mondo amatoriale. Chi non è troppo Almanacco Euro 8.00 giovane ricorderà le immagini ottenute dal cielo sopra Bologna da Sassi, Vac- Versare l’importo come spiegato qui sotto specificando la causale. -

Arp's Peculiar Galaxies - Supplementary Index the Deep Space CCD Atlas: North Presents 153 of the 338 Views Selected by Halton C
Arp's Peculiar Galaxies - Supplementary Index The Deep Space CCD Atlas: North presents 153 of the 338 views selected by Halton C. Arp in his 1966 Atlas of Peculiar Galaxies. An asterisk (*) indicates that the galaxy is not identified by its Arp number in the CCD Atlas or its index. The headings are the categories (a "preliminary" taxonomy) Arp established with his 1966 Atlas. Arp Common name Page Arp Common name Page Arp Common name Page Spiral Galaxies: 116 MESSIER 60 143 239 NGC 5278 + 79 152 LOW SURFACE BRIGHTNESS 120 NGC 4438 + 35 134* 240 NGC 5257 + 58 152 1 NGC 2857 99 122 NGC 6040A + B 167* 242 The Mice 143 2 UGC 10310 168* 123 NGC 1888 + 89 49 243 NGC 2623 93 3 MCG-01-57-016 245 124 NGC 6361 + comp 177* 244 NGC 4038 + 39 123* 5 NGC 3664 116 WITH NEARBY FRAGMENTS 245 NGC 2992 + 93 101 6 NGC 2537 90* 133 NGC 0541 15* 246 NGC 7838 + 37 1* SPLIT ARM 134 MESSIER 49 136* 248 Wild's Triplet 120 8 NGC 0497 14 135 NGC 1023 29* IRREGULAR CLUMPS 9 NGC 2523 91* 136 NGC 5820 161* 259 NGC 1741 group 47 12 NGC 2608 92* MATERIAL EMANATING FROM E 263 NGC 3239 107 DETACHED SEGMENTS GALAXIES 264 NGC 3104 104 13 NGC 7448 248* 137 NGC 2914 99* 266 NGC 4861 147 14 NGC 7314 245* 140 NGC 0275 + 74 9* 268 Holmberg II 91 15 NGC 7393 247 142 NGC 2936 + 37 100 16 MESSIER 66 114* 143 NGC 2444 + 45 85 Group Character 18 NGC 4088 124* CONNECTED ARMS THREE-ARMED Galaxies 269 NGC 4490 + 85 136* 19 NGC 0145 3 WITH ASSOCIATED RINGS 270 NGC 3395 + 96 110* 22 NGC 4027 123* 148 Mayall's Object 112 271 NGC 5426 + 27 156 ONE-ARMED WITH JETS 272 NGC 6050 + IC1174 168* -

The Orientation Parameters and Rotation Curves of 15 Spiral Galaxies�,
A&A 430, 67–81 (2005) Astronomy DOI: 10.1051/0004-6361:200400087 & c ESO 2005 Astrophysics The orientation parameters and rotation curves of 15 spiral galaxies, A. M. Fridman1,2,V.L.Afanasiev3, S. N. Dodonov3, O. V. Khoruzhii1,4,A.V.Moiseev3,5, O. K. Sil’chenko2,6, and A. V. Zasov2 1 Institute of Astronomy of the Russian Academy of Science, 48, Pyatnitskaya St., Moscow 109017, Russia 2 Sternberg Astronomical Institute, Moscow State University, University prospect 13, Moscow 119992, Russia 3 Special Astrophysical Observatory, Nizhnij Arkhyz, Karachaevo-Cherkesia 357147, Russia 4 Troitsk Institute for Innovation and Thermonuclear Researches, Troitsk, Moscow reg. 142092, Russia 5 Guest investigator of the UK Astronomy Data Centre 6 Isaac Newton Institute of Chile, Moscow Branch, Russia Received 13 December 2002 / Accepted 1 September 2004 Abstract. We analyzed ionized gas motion and disk orientation parameters for 15 spiral galaxies. Their velocity fields were measured with the Hα emission line by using the Fabry-Perot interferometer at the 6 m telescope of SAO RAS. Special attention is paid to the problem of estimating the position angle of the major axis (PA0) and the inclination (i) of a disk, which strongly affect the derived circular rotation velocity. We discuss and compare different methods of obtaining these parameters from kinematic and photometric observations, taking into account the presence of regular velocity (brightness) perturbations caused by spiral density waves. It is shown that the commonly used method of tilted rings may lead to systematic errors in the estimation of orientation parameters (and hence of circular velocity) being applied to galaxies with an ordered spiral structure. -
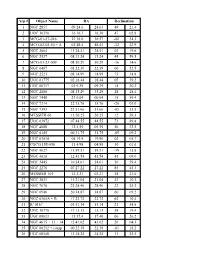
Arp # Object Name 1 NGC 2857 09 24.6 24.63 49 21.4 2 UGC 10310
Arp # Object Name RA Declination 1 NGC 2857 09 24.6 24.63 49 21.4 2 UGC 10310 16 16.3 16.30 47 02.8 3 MCG-01-57-016 22 36.6 36.57 -02 54.3 4 MCG-02-05-50 + A 01 48.4 48.43 -12 22.9 5 NGC 3664 11 24.41 24.41 03 19.6 6 NGC 2537 08 13.24 13.24 45 59.5 7 MCG-03-23-009 08 50.29 50.29 -16 34.6 8 NGC 0497 01 22.39 22.39 00 52.5 9 NGC 2523 08 14.99 14.99 73 34.8 10 UGC 01775 02 18.44 18.44 05 39.2 11 UGC 00717 01 9.39 09.39 14 20.2 12 NGC 2608 08 35.29 35.29 28 28.4 13 NGC 7448 23 0.04 00.04 15 59.4 14 NGC 7314 22 35.76 35.76 -26 03.0 15 NGC 7393 22 51.66 51.66 -05 33.5 16 MESSIER 66 11 20.25 20.25 12 59.3 17 UGC 03972 07 44.55 44.55 73 49.8 18 NGC 4088 12 5.59 05.59 50 32.5 19 NGC 0145 00 31.75 31.75 -05 09.2 20 UGC 03014 04 19.9 19.90 02 05.7 21 CGCG 155-056 11 4.98 04.98 30 01.6 22 NGC 4027 11 59.51 59.51 -19 15.8 23 NGC 4618 12 41.54 41.54 41 09.0 24 NGC 3445 10 54.61 54.61 56 59.4 25 NGC 2276 07 27.22 27.22 85 45.3 26 MESSIER 101 14 3.21 03.21 54 21.0 27 NGC 3631 11 21.04 21.04 53 10.3 28 NGC 7678 23 28.46 28.46 22 25.3 29 NGC 6946 20 34.87 34.87 60 09.2 30 NGC 6365A + B 17 22.72 22.72 62 10.4 31 IC 0167 01 51.14 51.14 21 54.8 32 UGC 10770 17 13.13 13.13 59 19.4 33 UGC 08613 13 37.4 37.40 06 26.2 34 NGC 4615 + 13 + 14 12 41.62 41.62 26 04.3 35 UGC 00212 + comp 00 22.38 22.38 -01 18.2 36 UGC 08548 13 34.25 34.25 31 25.5 37 MESSIER 77 02 42.68 42.68 00 00.8 38 NGC 6412 17 29.6 29.60 75 42.3 39 NGC 1347 03 29.7 29.70 -22 16.7 40 IC 4271 13 29.34 29.34 37 24.5 41 NGC 1232 + A 03 9.76 09.76 -20 34.7 42 NGC 5829 + IC 4526 15 2.7 02.70 23 19.9 43 -

1989Aj 98. .7663 the Astronomical Journal
.7663 THE ASTRONOMICAL JOURNAL VOLUME 98, NUMBER 3 SEPTEMBER 1989 98. THE IRAS BRIGHT GALAXY SAMPLE. IV. COMPLETE IRAS OBSERVATIONS B. T. Soifer, L. Boehmer, G. Neugebauer, and D. B. Sanders Division of Physics, Mathematics, and Astronomy, California Institute of Technology, Pasadena, California 91125 1989AJ Received 15 March 1989; revised 15 May 1989 ABSTRACT Total flux densities, peak flux densities, and spatial extents, are reported at 12, 25, 60, and 100 /¿m for all sources in the IRAS Bright Galaxy Sample. This sample represents the brightest examples of galaxies selected by a strictly infrared flux-density criterion, and as such presents the most complete description of the infrared properties of infrared bright galaxies observed in the IRAS survey. Data for 330 galaxies are reported here, with 313 galaxies having 60 fim flux densities >5.24 Jy, the completeness limit of this revised Bright Galaxy sample. At 12 /¿m, 300 of the 313 galaxies are detected, while at 25 pm, 312 of the 313 are detected. At 100 pm, all 313 galaxies are detected. The relationships between number counts and flux density show that the Bright Galaxy sample contains significant subsamples of galaxies that are complete to 0.8, 0.8, and 16 Jy at 12, 25, and 100 pm, respectively. These cutoffs are determined by the 60 pm selection criterion and the distribution of infrared colors of infrared bright galaxies. The galaxies in the Bright Galaxy sample show significant ranges in all parameters measured by IRAS. All correla- tions that are found show significant dispersion, so that no single measured parameter uniquely defines a galaxy’s infrared properties. -

University of Groningen Optical/NIR Stellar Absorption and Emission-Line
University of Groningen Optical/NIR stellar absorption and emission-line indices from luminous infrared galaxies Riffel, Rogério; Rodríguez-Ardila, Alberto; Brotherton, Michael S.; Peletier, Reynier; Vazdekis, Alexandre; Riffel, Rogemar A.; Martins, Lucimara Pires; Bonatto, Charles; Zanon Dametto, Natacha; Dahmer-Hahn, Luis Gabriel Published in: Monthly Notices of the Royal Astronomical Society DOI: 10.1093/mnras/stz1077 IMPORTANT NOTE: You are advised to consult the publisher's version (publisher's PDF) if you wish to cite from it. Please check the document version below. Document Version Publisher's PDF, also known as Version of record Publication date: 2019 Link to publication in University of Groningen/UMCG research database Citation for published version (APA): Riffel, R., Rodríguez-Ardila, A., Brotherton, M. S., Peletier, R., Vazdekis, A., Riffel, R. A., ... Trevisan, M. (2019). Optical/NIR stellar absorption and emission-line indices from luminous infrared galaxies. Monthly Notices of the Royal Astronomical Society, 486(4), 3228-3247. https://doi.org/10.1093/mnras/stz1077 Copyright Other than for strictly personal use, it is not permitted to download or to forward/distribute the text or part of it without the consent of the author(s) and/or copyright holder(s), unless the work is under an open content license (like Creative Commons). Take-down policy If you believe that this document breaches copyright please contact us providing details, and we will remove access to the work immediately and investigate your claim. Downloaded from the University of Groningen/UMCG research database (Pure): http://www.rug.nl/research/portal. For technical reasons the number of authors shown on this cover page is limited to 10 maximum. -

Seen Galaxies Count Ref1 Ref2 Con Visual Scale Mag SBR SIZE M Distance Rv Dist COMMENTS
Seen galaxies Count ref1 ref2 con visual_scale mag SBR SIZE_M Distance Rv dist COMMENTS 1. NGC 224 M 31 AND 5 3.4 13.5 189 2.6 -14 Very large and bright 2. NGC 3031 M 81 UMA 4 6.9 13.2 24.9 12 -3 Fine large galaxy 3. NGC 598 M 33 TRI 3 5.7 14.2 68.7 2.8 -10 Large faint glow in square of stars 4. NGC 4594 M 104 VIR 3 8.0 11.6 8.6 30 48 Moon therefore little detail 5. NGC 221 M 32 AND 3 8.1 12.4 8.5 2.6 -10 Small but easy to see 6. NGC 4472 M 49 VIR 3 8.4 13.2 9.8 53 43 Lovely fuzzy galaxy 7. NGC 3034 M 82 UMA 3 8.4 12.5 10.5 12 13 Could make out bright and dark patches 8. NGC 4258 M 106 CVN 3 8.4 13.6 17.4 24 21 Fine large oval galaxy. So much brighter than most I have been looking at recently. 9. NGC 4826 M 64 COM 3 8.5 12.7 10.3 24 21 Easy galaxy to see 10. NGC 4486 M 87 VIR 3 8.6 13 8.7 51 57 Bright ball 11. NGC 4649 M 60 VIR 3 8.8 12.9 7.6 54 49 Lovely view with three galaxies visible. M60 is the brightest of the three. A nice bright ball of stars 12. NGC 3115 MCG - 1-26- 18 SEX 3 8.9 11.9 7.3 33 29 Bright spindle 13. -

Box-And Peanut-Shaped Bulges: I. Statistics
A&A manuscript no. ASTRONOMY (will be inserted by hand later) AND Your thesaurus codes are: ASTROPHYSICS 11 (11.05.2; 11.19.2; 11.19.7; 11.19.6) November 9, 2018 Box- and peanut-shaped bulges ⋆ I. Statistics R. L¨utticke, R.-J. Dettmar, and M. Pohlen Astronomisches Institut, Ruhr-Universit¨at Bochum, D-44780 Bochum, Germany email: [email protected] Received 11 May 2000; accepted 14 June 2000 Abstract. We present a classification for bulges of a com- External cylindrically symmetric torques (May et al. plete sample of ∼ 1350 edge-on disk galaxies derived from 1985) or mergers of two disk galaxies (Binney & Petrou the RC3 (Third Reference Catalogue of Bright Galaxies, 1985, Rowley 1988) as origins of b/p bulges require very de Vaucouleurs et al. 1991). A visual classification of the special conditions (Bureau 1998). Therefore such evolu- bulges using the Digitized Sky Survey (DSS) in three types tionary scenarios can explain only a very low frequency of of b/p bulges or as an elliptical type is presented and sup- b/p bulges. Accretion of satellite galaxies is a formation ported by CCD images. NIR observations reveal that dust process of b/p bulges (Binney & Petrou 1985, Whitmore & extinction does almost not influence the shape of bulges. Bell 1988), which could produce a higher frequency of b/p There is no substantial difference between the shape of bulges. However, an oblique impact angle of the satellite bulges in the optical and in the NIR. Our analysis reveals is needed for the formation of a b/p bulge and a mas- that 45% of all bulges are box- and peanut-shaped (b/p).