— Technical Guide No. 8 Electrical Braking
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

ACSM1 System Engineering Manual
ACSM1 System Engineering Manual 2 3 ACSM1-04 Drive Modules System Engineering Manual 3AFE 68978297 REV A EN EFFECTIVE: 08.10.2007 PDM Vault ID: 00579251 2007 ABB Oy. All rights reserved. 4 5 Safety instructions Never work on the drive, the braking chopper circuit, the motor cable or the motor when input power is applied to the drive. After disconnecting input power, always wait for 5 minutes to let the intermediate circuit capacitors discharge before you start working on the drive, control cabling, motor or motor cable. Even when input power is not applied to the drive, externally supplied control circuits may carry dangerous voltages. Always ensure by measuring that no voltage is actually present. A rotating permanent magnet motor can generate a dangerous voltage. Lock the motor shaft mechanically before connecting a permanent magnet motor to the drive, and before doing any work on a drive system connected to a permanent magnet motor. For complete safety instructions see the ACSM1-04 Drive Modules (0.75 to 45 kW) Hardware Manual (code: 3AFE68797543 [English]). 6 Table of contents Safety instructions ................................................................................................................... 5 Table of contents...................................................................................................................... 6 About this manual .................................................................................................................... 8 Compatibility .............................................................................................................................. -

Siemens On-Stage Powerpoint-Template
Electromobility Solutions for Modern Haul Trucks 2017 Haulage & Loading Exhibition / Conference Phoenix, Arizona USA Unrestricted © Siemens Industry, Inc. 2017 usa.siemens.com/mining Introduction What is Electromobility? Electromobility is a general term for the development of electric- powered drivetrains designed to shift vehicle design away from the use of fossil fuels and carbon gas emissions. • Hybrid Electric Vehicles (Internal Combustion Engine (ICE) and batteries w/ Electric motor) • Plug-in Electric Vehicles (HEV that can be externally charged) • Battery Electric Vehicles (all electric vehicle that can be externally charged) Electric Drive Technology and Charging Solutions for Mobility. Unrestricted © Siemens Industry, Inc. 2017 2017 Haulage & Loading Exhibition and Conference Page 2 May 8, 2017 Electromobility Solutions for Modern Haul Trucks Mechanical Vehicle (MV) w/ On-board Diesel Engine Traditional Powertrain Main Components: - Diesel Engine - Torque Converter - Drive Shaft (Cardan) - Transmission - Differential - Gearbox Disadvantages: - Low efficiency - High maintenance costs Unrestricted © Siemens Industry, Inc. 2017 2017 Haulage & Loading Exhibition and Conference Page 3 May 8, 2017 Electromobility Solutions for Modern Haul Trucks Electric Vehicle (EV) w/ On-board Diesel Engine Electrical Drivetrain replaces Mechanical Drivetrain, keeps the diesel engine Main Components: - Diesel engine - Alternator w/ Rectifier - Inverters - Traction motors - Braking chopper/Grid resistor Benefits - Higher efficiency - Electrical braking -

Review of the State-Of-The-Art in Power Electronics Suitable for 10-Kw Military Power Systems
ORNL/TM-2003/209 REVIEW OF THE STATE-OF-THE-ART IN POWER ELECTRONICS SUITABLE FOR 10-KW MILITARY POWER SYSTEMS R. H. Staunton B. Ozpineci T. J. Theiss L. M. Tolbert* Oak Ridge National Laboratory *The University of Tennessee (Joint appointment with the Oak Ridge National Laboratory and the University of Tennessee) This report was prepared as an account of work sponsored by an agency of the United States Government. Neither the United States Government nor any agency thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise, does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof. ORNL/TM-2003/209 Engineering Science & Technology Division REVIEW OF THE STATE-OF-THE-ART IN POWER ELECTRONICS SUITABLE FOR 10KW MILITARY POWER SYSTEMS R. H. Staunton B. Ozpineci T. J. Theiss L. M. Tolbert October 2003 Manuscript completed: September 2003 Date Published: December 2003 Prepared by the OAK RIDGE NATIONAL LABORATORY Oak Ridge, Tennessee 37831 managed by UT-BATTELLE, LLC for the U.S. DEPARTMENT OF ENERGY Under contract DE-AC05-00OR22725 TABLE OF CONTENTS Page LIST OF FIGURES ............................................................................................................................. -

Brushless DC Electric Motor
Please read: A personal appeal from Wikipedia author Dr. Sengai Podhuvan We now accept ₹ (INR) Brushless DC electric motor From Wikipedia, the free encyclopedia Jump to: navigation, search A microprocessor-controlled BLDC motor powering a micro remote-controlled airplane. This external rotor motor weighs 5 grams, consumes approximately 11 watts (15 millihorsepower) and produces thrust of more than twice the weight of the plane. Contents [hide] 1 Brushless versus Brushed motor 2 Controller implementations 3 Variations in construction 4 AC and DC power supplies 5 KM rating 6 Kv rating 7 Applications o 7.1 Transport o 7.2 Heating and ventilation o 7.3 Industrial Engineering . 7.3.1 Motion Control Systems . 7.3.2 Positioning and Actuation Systems o 7.4 Stepper motor o 7.5 Model engineering 8 See also 9 References 10 External links Brushless DC motors (BLDC motors, BL motors) also known as electronically commutated motors (ECMs, EC motors) are electric motors powered by direct-current (DC) electricity and having electronic commutation systems, rather than mechanical commutators and brushes. The current-to-torque and frequency-to-speed relationships of BLDC motors are linear. BLDC motors may be described as stepper motors, with fixed permanent magnets and possibly more poles on the rotor than the stator, or reluctance motors. The latter may be without permanent magnets, just poles that are induced on the rotor then pulled into alignment by timed stator windings. However, the term stepper motor tends to be used for motors that are designed specifically to be operated in a mode where they are frequently stopped with the rotor in a defined angular position; this page describes more general BLDC motor principles, though there is overlap. -

Electrical Braking 2 Technical Guide No.8 - Electrical Braking Contents
Technical Guide No. 8 Electrical Braking 2 Technical Guide No.8 - Electrical Braking Contents 1. Introduction ........................................................... 5 1.1 General .................................................................... 5 1.2 Drive applications map according to speed and torque ..................................................................... 5 2. Evaluating braking power................................... 7 2.1 General dimension principles for electrical braking ..................................................................... 7 2.2 Basics of load descriptions ................................... 8 2.2.1 Constant torque and quadratic torque...... 8 2.2.2 Evaluating brake torque and power .......... 8 2.2.3 Summary and Conclusions ........................ 12 3. Electrical braking solutions in drives .............. 13 3.1 Motor Flux braking ................................................. 13 3.2 Braking chopper and braking resistor .................. 14 3.2.1 The energy storage nature of the frequency converter ................................... 14 3.2.2 Principle of the braking chopper ............... 15 3.3 Anti-parallel thyristor bridge configuration ........... 17 3.4 IGBT bridge configuration...................................... 19 3.4.1 General principles of IGBT based regeneration units ....................................... 19 3.4.2 IGBT based regeneration-control targets . 19 3.4.3 Direct torque control in the form of direct power control ............................................. -

GPD 503 Technical Manual Efesotomasyon.Com - Yaskawa Ac Drive,Servo Motor
efesotomasyon.com - Yaskawa ac drive,servo motor MagneTe k GPD 503 Technical Manual efesotomasyon.com - Yaskawa ac drive,servo motor GPD 503 SIMPLIFIED START-UP PROCEDURE This procedure will quickly get you up and running by Digital Operator keypad or user supplied remote operator control. It assumes that the GPD 503 and motor are correctly wired (see pages 1-8 thru 1-15), and start-up is to be performed without any changes to factory set constants. Detailed information on the many other features of this drive will be found in later sections of this manual. INSTALLATION 1. Be certain your input voltage source, motor, and drive name plates are all marked either 230V, 460V, or 575V. Other voltages can be used, but require additional programming, see Section 2. 2. Mount drive on a vertical surface with adequate space for air circulation. 3. Remove front cover, fit conduit to bottom plate, and connect power and ground wires as shown. CAUTION Be certain you connect input power to terminals L1, L2, and L3 only, or serious damage will result. Connect motor to terminals T1, T2, and T3 only. KEYPAD OPERATION 1. Replace cover and apply input power - keypad display shows "F00.00 "; DRIVE, FWD, and STOP lampS are on. Press and hold JOG key, noting direction of motor rotation. If it is incorrect, remove power, wait for “CHARGE” light to go out, then switch wires between terminals T1, and T2. Replace cover, and apply input power. 2. Run, Stop, and Frequency (Speed) - Here, the terms frequency and speed are used interchangeably. -
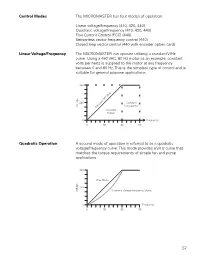
57 Control Modes the MICROMASTER Has Four
Control Modes The MICROMASTER has four modes of operation: Linear voltage/frequency (410, 420, 440) Quadratic voltage/frequency (410, 420, 440) Flux Current Control (FCC) (440) Sensorless vector frequency control (440) Closed loop vector control (440 with encoder option card) Linear Voltage/Frequency The MICROMASTER can operate utilizing a standard V/Hz curve. Using a 460 VAC, 60 Hz motor as an example, constant volts per hertz is supplied to the motor at any frequency between 0 and 60 Hz. This is the simplest type of control and is suitable for general purpose applications. Quadratic Operation A second mode of operation is referred to as a quadratic voltage/frequency curve. This mode provides a V/Hz curve that matches the torque requirements of simple fan and pump applications. 57 Flux Current Control Stator current (IS) is made up of active and reactive current. The reactive current component of stator current produces the rotating magnetic field. The active current produces work. Motor nameplate data is entered into the drive. The drive estimates motor magnetic flux based on the measured reactive stator current and the entered nameplate data. Proprietary internal computer algorithms attempt to keep the estimated magnetic flux constant. If the motor nameplate information has been correctly entered and the drive properly set up, the flux current control mode will usually provide better dynamic performance than simple V/Hz control. Flux current control automatically adapts the drive output to the load. The motor is always operated at optimum efficiency. Speed remains reliably constant even under varying load conditions. Sensorless Vector Control In the past, the dynamic response of a DC motor was generally considered significantly better than an AC motor. -

Intelligent Low Voltage Solid State Motor Control Products with Next Generation MX2/MX3 Technology
Intelligent Low Voltage Solid State Motor Control Products with next generation MX2/MX3 technology Low Voltage Solid State Starters MX2 Control Technology Next Generation Intelligent Motor Control Next Generation Intelligent Motor Control • Mission critical reliability • Patented soft start technology • Integral digital protection and metering • Continuous and integral bypass chassis • RXE redundant configurations • MXP modular, prepackaged starters MX2 Board • Reversing, two-speed, wound rotor • Synchronous, dc injection braking • 24/7 service and support MX2 Control Highlights The MX2 control technology from Benshaw provides a powerful, flexible, intelligent low voltage motor control platform. MX2-based controls offer multiple, user selectable starting modes, an increased selection of configurable digital and analog I/O’s, comprehensive built-in metering capabilities, unprecedented onboard protection and an easy to use, intuitive user interface. Our control board terminal configuration—coupled with programmable burden CT settings—makes Benshaw’s MX2 technology an excellent choice for a wide range of intelligent, soft start motor control applications. Benshaw’s MX2-based low voltage motor controls raise the bar for intelligent, low-cost, soft start motor control. When you factor in our unique three-year factory warranty and 24/7 comprehensive technical 2 Optional Keypad support, we think you’ll find Benshaw’s MX -based controls to be an excellent value. Standard Features: • High performance motor control with multiple • Power stack thermistor -

4215Ijci19.Pdf
International Journal on Cybernetics & Informatics (IJCI) Vol. 4, No. 2, April 2015 SURVEY OF CONVENTIONAL &NEW GENERATION ADVANCED D.C.BRAKING SYSTEM OF 3-PHASE SQUIRREL CAGE INDUCTION MOTOR WITH VFD Deepak Kotkar 1, Upama Bose 2, Atul Gupta 3, R. Rajamanickam 4, Sneha Sankar 5 1M.Tech Scholar, VJTI, Mumbai, Maharashtra 400019, 2,5 M.Tech Scholar, VIT University, Katpadi, Vellore, Tamil Nadu, 632014, 3,4 Larsen & Toubro, R&D, Electrical & automation, Mahape, Navi Mumbai, ABSTRACT Any variable frequency drive requires an efficient and controlled braking system. Therefore, different braking techniques have been the subject area of researchers to enhance the performance as well as overall life of the drives. In this paper, a literature study is made of various existing braking methods, focused on induction motor (IM) drive performance. The braking methods are compared and summarized based on speed range, braking time and efficiency of 3-phase squirrel cage IM drive. Finally, an advancedD.C. braking technique is presented where braking torque in terms of varyingD.C.signal is injected into the stator windings using fully controlled Space Vector Pulse Width Modulation pulses (SVPWM). A method has been described for providing occasional fast, smooth and controlled braking torque from a non-regenerative VFD, without additional power circuits. Simulations are performed in MATLAB/Simulink, tested and validated on Digital signal processor (DSP) based drive. Test results are presented in this paper. KEYWORDS 3-Phase Induction Motor, Braking, Conventional, AC Drive, VFD, MATLAB/Simulink, DSP. 1. INTRODUCTION Three-phase induction motor drives are extensively used in different sectors of drives industry, but it is a challenge to stop them in short period of timeespecially for high inertia loads. -

Leroy-Somer Moteurs AC Imfinity®
IMfinity® Liquid cooled motors - LC series 3-phase induction motors IE3 Premium efficiency Variable and fixed speed Frame size 315 to 500 150 to 1500 kW The LC induction motors in this catalog are designed to achieve very high efficiency levels and operate at variable speed. This catalog contains technical information about motors in the IE3 efficiency class (Premium efficiency) which can be used on an A.C. supply and also on a drive. On request, Leroy-Somer is able to offer IE4 motor solutions. All the motors in this catalog can be used at variable speed depending on the specified conditions. All 2, 4 and 6-pole motors, rated 0.75 to 375 kW, offered for sale on the European Union market must be efficiency class IE3 or IE2 and used with a variable speed drive: - from 01/01/2015 for 7.5 to 375 kW ratings - from 01/01/2017 for 0.75 to 375 kW ratings In addition, to be eligible for efficiency class IE3, the water inlet temperature for water-cooled motors must be between 0°C and 32°C. IMfinity® - LC Liquid-Cooled 3-Phase Induction Motors Contents GENERAL TECHNICAL CHARACTERISTICS Introduction ...........................................................................4 Designation.........................................................................50 Quality Commitment .............................................................5 Identification .......................................................................51 Directive and Standards Relating to Motor Efficiency............6 Description of an LC Motor basic conception ......................53 -

Emergency Dc Injection Breaking
ISSN: 2455-2631 © November 2020 IJSDR | Volume 5, Issue 11 EMERJENCY DC INJENCTION BREAKING Mrs Kalpana S, Mr Kiran Kumar G R, Mrs Manasa B, Mrs Shruthi S Assistant Professor, Department of Electrical and electronics Engineering, PESITM Shivamogga Abstract: The emergency dc injection breaking presents a practical design for the implement model will be shown and performances will be station of an improved non-regenerative emergency braking system. The realization of an industrial compared for different motors. The testing session has shown that the model was able to handle up to 5A output and withstand up to 30Vpower line. The proposed eme1rgency braking method can brake most induction machines under 4 seconds. Design considerations, advantage and drawback are then discussed. Keywords: Dynamic braking, Induction motors 1. INTRODUCTION The term braking comes from the term brake. the brake is an equipment to reduce the speed of any moving or rotating equipment, like vehicles, locomotives. The process of applying brakes can be termed as braking. DC injection breaking is a method of slowing ac electric motor. A dc voltage is injected into the winding of ac motor after the ac voltage is disconnected providing breaking for the rotor Three-phase induction motor drives are extensively used in different sectors of drives industry, but it is a challenge to stop them in short period of time especially for high inertia loads. To control an electric machine by electric drives, its braking system is very important because it helps to decrease the speed of the motor according to will and necessity. Electronic D.C. -

SERIES 23H AC Servo Control
AC SERVO DRIVE SERIES 23H AC Servo Control Installation & Operating Manual 1/99 MN723 Table of Contents Section 1 Quick Start Guide . 1-1 Overview . 1-1 Quick Start Checklist . 1-1 Quick Start Procedure . 1-2 Section 2 General Information . 2-1 Overview . 2-1 Limited Warranty . 2-2 Safety Notice . 2-3 Section 3 Receiving & Installation . 3-1 Receiving & Inspection . 3-1 Physical Location . 3-1 Control Installation . 3-2 Through the Wall Mounting . 3-2 Keypad Installation Procedure . 3-2 Optional Remote Keypad Installation . 3-3 Electrical Installation . 3-4 System Grounding . 3-4 Line Impedance . 3-6 Line Reactors . 3-7 Load Reactors . 3-7 AC Main Circuit Considerations . 3-8 Protection Devices . 3-8 Power Disconnect . 3-8 Wire Size and Protection Devices . 3-8 AC Line Connections . 3-10 Reduced Input Voltage Derating . 3-10 380-400 VAC Operation . 3-10 Three Phase Motor and Control Connections . 3-11 Single Phase Input Power Considerations. 3-14 Single Phase Control Derating . 3-14 Size A, B and C2 Single Phase Power Installation. 3-15 Size C and D Single Phase Power Installation. 3-17 Size E Single Phase Power Installation. 3-19 Size F Single Phase Power Installation. 3-21 Optional Dynamic Brake Hardware . 3-23 Physical Installation . 3-23 Electrical Installation . 3-24 MN723 Table of Contents i M-Contactor . 3-27 Resolver Feedback . 3-27 Simulated Encoder Output . 3-28 Home (Orient) Switch Input . 3-29 Control Circuit Connections . 3-30 Keypad Operating Mode . 3-30 Standard Run 3 Wire Mode Connections. 3-32 15 Speed 2-Wire Mode Connections.