Phd Dissertation
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Econstor Wirtschaft Leibniz Information Centre Make Your Publications Visible
A Service of Leibniz-Informationszentrum econstor Wirtschaft Leibniz Information Centre Make Your Publications Visible. zbw for Economics Müller, Holger; Kroll, Eike Benjamin; Vogt, Bodo Conference Paper WHEN JUDGMENTS AND PREFERENCES FAIL TO CONFORM: RESEARCH ON PREFERENCE REVERSALS FOR PRODUCT PURCHASES Beiträge zur Jahrestagung des Vereins für Socialpolitik 2010: Ökonomie der Familie - Session: Consumer Behaviour and Intertemporal Choice, No. G17-V1 Provided in Cooperation with: Verein für Socialpolitik / German Economic Association Suggested Citation: Müller, Holger; Kroll, Eike Benjamin; Vogt, Bodo (2010) : WHEN JUDGMENTS AND PREFERENCES FAIL TO CONFORM: RESEARCH ON PREFERENCE REVERSALS FOR PRODUCT PURCHASES, Beiträge zur Jahrestagung des Vereins für Socialpolitik 2010: Ökonomie der Familie - Session: Consumer Behaviour and Intertemporal Choice, No. G17-V1, Verein für Socialpolitik, Frankfurt a. M. This Version is available at: http://hdl.handle.net/10419/37400 Standard-Nutzungsbedingungen: Terms of use: Die Dokumente auf EconStor dürfen zu eigenen wissenschaftlichen Documents in EconStor may be saved and copied for your Zwecken und zum Privatgebrauch gespeichert und kopiert werden. personal and scholarly purposes. Sie dürfen die Dokumente nicht für öffentliche oder kommerzielle You are not to copy documents for public or commercial Zwecke vervielfältigen, öffentlich ausstellen, öffentlich zugänglich purposes, to exhibit the documents publicly, to make them machen, vertreiben oder anderweitig nutzen. publicly available on the internet, or to distribute or otherwise use the documents in public. Sofern die Verfasser die Dokumente unter Open-Content-Lizenzen (insbesondere CC-Lizenzen) zur Verfügung gestellt haben sollten, If the documents have been made available under an Open gelten abweichend von diesen Nutzungsbedingungen die in der dort Content Licence (especially Creative Commons Licences), you genannten Lizenz gewährten Nutzungsrechte. -

Electric Goes Down with Pole in M-21/Alden Nash Accident YMCA
25C The Lowell Volume 14, Issue 14 Serving Lowell Area Readers Since 1893 Wednesday, February 14, 1990 Electric goes down with pole in M-21/Alden Nash accident An epileptic seizure suffered by Daniel Barrett was the cause of his vehicle leaving the road. The electrical pole was broken in three different places. Roughly 200 homes and Zeigler Ford sign and the businesses were without elec- power pole about 10-feet tricity for I1/: hours (5-7:30 above ground before the veh- p.m.) on Thursday (Feb. 8) icle came to a rest on Alden following a one-car accident Nash. at the comer of M-21 and According to Kent County Alden Nash. Deputy Greg Parolini a wit- 0 The Kent County Sheriff ness reported that the vehicle Department s report staled accelerated as it left the road- that Daniel Joseph Barrett, way. 19, of Lowell, was eastbound Barrett incurred B-injuries on M-21 when he suffered an (visible injuries) and was epileptic seizure, causing his transported to Blodgett Hos- vehicle to cross the road and pital by Lowell Ambulance. enter a small dip in the Barrett's collision caused boulevard. Upon leaving the the electrical pole to break in Following Thursday evening's accident at M-21 and Daniel Barrett suffered B-injuries (visible injuries) in low area, the car became air- three different places. A Low- borne, striking the Harold Alden Nash, a Lowell Light and Power crew was busy Thursday's accident. Acc., cont'd., pg. 2 erecting a new electrical pole. # YMCA & City sign one year agreement Alongm • Main Street rinjsro The current will be a detriment to the pool ahead of time if something is and maintenance of the this year. -

Edible Rocks Are They?”
Exploring Meteorite Mysteries “What Lesson 8 Edible Rocks are they?” Objectives About This Lesson Students will: This lesson has been designed as a comfortable • observe and describe physical characteristics of an edible introduction to describing sample in preparation for describing rock or meteorite meteorites. It helps students samples. become better observers by • work cooperatively in a team setting. making a connection between • use communication skills, both oral and written. the familiar (candy bars) and the unfamiliar (meteorites). Materials Edible “rocks” are used in a ❑ prepared edible samples (see attached list, pg. 8.3 and scientific context, showing recipes, pg. 8.4) students the importance of ❑ small plastic bags for samples ❑ knife observation, teamwork and ❑ “Field Note” Sample Descriptions of candy bars, enlarged and cut communication skills. In into numbered segments (pgs. 8.7-8.10). everyday terms, students draw Note: If included recipes are not used, then the descriptions may and describe the food. need to be revised by the classroom teacher to more accurately Students will pair their obser- describe the actual samples. vations with short descriptions ❑ Student Procedure (pg. 8.5, one sheet per team of two) that are in geologic “Field ❑ colored pencils for each team Note” style. As the teacher ❑ pen or pencil and class review, appropriate geologic terminology may be substituted by the teacher and subsequently embraced by even very young students. The last part of this activity allows the student to describe rock specimens before they move to meteorite samples in the Meteorite Sample Disk. Cut surface of “edible rock.” eec Procedure Note: Objectives and a Advanced Preparation formal vocabulary 1. -

Wealth and Poverty in the United States 2
WEALTH AND POVERTY IN THE UNITED STATES ! Jeremy Cloward, Ph.D. ! 1 “The…truth is that the rich are the great cause of poverty” ! ! Michael Parenti (American political scientist, historian and media analyst) 1 INTRODUCTION ! By almost any measure the United States is a wealthy nation. In 2014, according to the IMF, World Bank and the United Nations, the US had the highest GDP in the world – standing at more than $16 trillion dollars. China is second with a GDP just over $8 trillion dollars. In fact, the Organization for Economic Co-operation and Development (OECD) reported in 2012 that the United States had the highest average wage in the world at some $55,000 dollars per year even if it that wage ranked 4th amongst the world’s nations in terms of purchasing power.2 However, contrary to Adam Smith’s most famous assertion about prosperity and self-interest in the marketplace, the “invisible hand” in the United States has not resulted in riches for all but instead great wealth for some, economic inequality for many and unrelenting poverty for the rest. ! 2 Income and Wealth Inequality ! For some time, income and wealth in the United States have increasingly become concentrated into the hands of fewer and fewer people and powerful corporations. This, in addition to the continual neo-liberalization of US society, i.e., increased privatization and !1 reduced funding for social programs, has created a situation where day-to-day living has become more expensive yet the median wage “has been stagnant” for the great majority of the American people.3 Today, this has created a situation where economic inequality is greater than at almost any period in US history. -
Exploring Meteorite Mysteries a TeacherS Guide with Activities for Earth and Space Sciences EG-1997-08-104-HQ National Aeronautics and Space Administration
Educational Product National Aeronautics and Teachers Grades 5-12 Space Administration Exploring Meteorite Mysteries A Teachers Guide with Activities for Earth and Space Sciences EG-1997-08-104-HQ National Aeronautics and Space Administration Exploring Meteorite Mysteries A Teachers Guide with Activities for Earth and Space Sciences Office of Space Science Solar System Exploration Division Office of Human Resources and Education Education Division August 1997 This publication is in the Public Domain and is not copyrighted. Permission is not required for duplication. Acknowledgements This teacher’s guide was developed in a partnership between scientists in the Planetary Materials Office, at NASA’s Johnson Space Center in Houston, Texas, and teachers from local school districts. NASA and Contractor Staff Teachers On the Cover— Marilyn Lindstrom JoAnne Burch Project Coordinator and Meteorite Curator Pearland ISD, Several aspects of a meteorite NASA Johnson Space Center Elementary fall are depicted on the cover. Houston, Texas Pearland, Texas The background is a painting created by an eyewitness of Karen Crowell Jaclyn Allen the Sikhote-Alin fireball. At Scientist and Science Education Specialist Pasadena ISD, Lockheed Martin Engineering & Sciences Co. Elementary the top is the asteroid Ida, a Houston, Texas Pasadena, Texas possible source of meteorites. At the bottom is Meteor Allan Treiman* and Carl Allen Roy Luksch Crater in Arizona—the first Alvin ISD, Planetary Scientists identified meteorite impact Lockheed Martin Engineering & Sciences Co. High School Houston, Texas Alvin, Texas crater. Anita Dodson Karen Stocco Graphic Designer Pasadena ISD, Lockheed Martin Engineering & Sciences Co. High School Houston, Texas Pasadena, Texas Bobbie Swaby Pasadena ISD, Middle School National Aeronautics and Pasadena, Texas Space Administration Lyndon B. -

TSB-A-93 (38)S:6/93:Mr. Wynn Vogel,Petition No. S930107B,Tsba9338s
New York State Department of Taxation and Finance Taxpayer Services Division TSB-A-93 (38)S Sales Tax Technical Services Bureau June 21, 1993 STATE OF NEW YORK COMMISSIONER OF TAXATION AND FINANCE ADVISORY OPINION PETITION NO. S930107B On January 7, 1993 a Petition for Advisory Opinion was received from Mr. Wynn Vogel, 1865-77th Street (C-9), Brooklyn, New York 11214-1233. The issues raised by Petitioner, Wynn Vogel, are: (1) Whether the sales of a product called "PB Max" are subject to sales tax. (2) Whether the sales of a product called "Twix" are subject to sales tax. PB Max is a product which is sold both as an individual item and in a family carton of six individually wrapped items. PB Max, according to the packaging, is a "real peanut butter snack, made with real peanut butter, crunchy wholegrain cookie, all covered in pure milk chocolate". According to the label on the packaging, its principal ingredients are peanut butter, milk chocolate, oats, flour, partially hydrogenated vegetable oil and sugar. Twix is also a product which is sold as an individual item and in a family pack. Twix, according to the packaging is a "chocolate caramel cookie". According to the label on the packaging, its principal ingredients are milk chocolate, enriched flour, partially hydrogenated soybean oil, sugar and corn syrup. Section 1115 of the Tax Law provides, in part: (a) Receipts from the following shall be exempt from the tax on retail sales imposed under subdivision (a) of section eleven hundred five and the compensating use tax imposed under section eleven hundred ten: (1) Food, food products, beverages, dietary foods and health supplements, sold for human consumption but not including (i) candy and confectionery ... -

Documentation for the CSAFII/DHKS 1989-91 Data
Differences Between Current and Original Release of CSFII/DHKS 1989-91 Dataset and Documentation Please be advised that the data available from past USDA food consumption surveys reflect the foods and their nutrient values that were available at the time of the particular survey. Each survey was designed to assess the dietary status of the U.S. population at that particular time. It is important to consider that survey methods and operations including questionnaire wording, data processing methods, and the survey nutrient database used to calculate the dietary intake were updated from survey to survey based on new data and methods available at the time. Comparing data across surveys must take into account these types of changes. Some research has addressed the impact of changes in methods and/or databases between selected surveys. References are included in the respective surveys’ report sections on this site. Please study the complete dataset documentation before using the dataset. Nearly all the information provided with the original release continues to be applicable for the new release. However, some changes have been made to data formats and other items, so please keep the following points in mind as you read the documentation: • The data are now available online in SAS7 files (.sas7bdat) rather than on magnetic tape in ASCII fixed format files or on CD-ROM to be accessed using SETS software. • The formats documents from the original release (e.g., rt15.fmt) are superseded by new documents (e.g., rt15fmt.txt). • References to implied decimals are no longer relevant. The SAS variables carry the appropriate number of decimal places. -

PAUL C. GONDEK, Phd Cell: 908.391.3077, [email protected] [email protected]
PAUL C. GONDEK, PhD Cell: 908.391.3077, [email protected] [email protected] OBJECTIVE To use my diverse professional and educational background to teach and mentor students in order to prepare them for productive professional and civic lives in the context of a rapidly changing, learning- intensive, globalizing world. EDUCATION 2015- Present Assorted workshops and conferences on teaching and assessment methods 2005 Vistage Chair Vistage International, San Diego, California. Trained Executive Coach and facilitator of advisory groups of CEOs and senior executives. 2000 Certified New Product Development Professional Product Development and Management Association, Chicago, IL 1998 Certified Management Consultant Institute of Management Consultants, Washington, D.C. 1981 Post-doctoral Fellow Western Psychiatric Institute, The University of Pittsburgh, Pittsburgh, PA Psychiatric Epidemiology. Statistical analysis/research design member of team that studied the effects on resident mental health of the Three Mile Island nuclear accident. 1979 Ph.D. The University of Connecticut, Storrs, CT, Social Psychology Supported by research and teaching fellowships 1979 MS The University of Connecticut, Storrs, CT, Statistics (double majored with psychology) 1978 MA The University of Connecticut, Storrs, CT, Social Psychology 1974 BS Drexel University, Philadelphia, PA. Psychology/Sociology/Anthropology, an Interdisciplinary Major in the College of Humanities and Social Sciences. Graduated with Honors. National Merit Scholar SUMMARY OF TEACHING, FACILITATION -

USE the 5 CLUES in Your Kitchen!
NUTRITION DETECTIVES™ A Katz & Katz Production USE THE 5 CLUES In Your Kitchen! Directions This is a chance for your family to use your Nutrition Detectives™ skills at home! It’s best if the children and adults in the family work on this project together. 1. Review the 5 clues from the Nutrition Detectives™ program on page 2. 2. Look at the lists of “CLUED-IN” and “CLUE-LESS” food products on pages 5 to 12. The lists show examples of breads, crackers, cereals, cereal bars, cookies, chips, juices & drinks, and peanut butter & spreads that are either “CLUED-IN” or “CLUE-LESS” food choices based on the 5 clues. 3. Look in your refrigerator and kitchen cupboards for foods that come in boxes, bottles, jars, cartons, or packages. Decide whether they are “CLUED-IN” and “CLUE-LESS” choices based on the 5 clues from Nutrition Detectives.™ Along with the 5 clues, use the ingredient lists and the Nutrition Facts labels on the food products to decide. 4. Use the guidelines on pages 3 and 4 to create a list of some of the foods in your home. For each food, write down the brand name, the kind of food (such as white bread), whether it’s a “CLUED-IN” or “CLUE-LESS” choice, and the reason why. 5. If you find that many of the foods in your home tend to be “CLUE-LESS” choices, think about how your family can use Nutrition Detectives™ skills to make more healthful choices in the future. You might be able to find foods that are similar to the ones that you usually buy, but that are more healthful based on the “5 clues.” The idea is to keep the healthful food products in your home and replace those that are less healthful. -
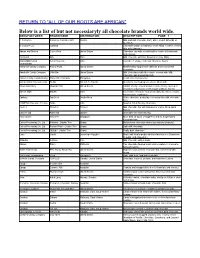
Below Is a List of but Not Necessiaryly All Chocolate Brands World Wide. MANUFACTURER BRAND NAME DISTRIBUTION DESCRIPTION PAGE 1 A
RETURN TO “ALL OF OUR ROOTS ARE AFRICAN" Below is a list of but not necessiaryly all chocolate brands world wide. MANUFACTURER BRAND NAME DISTRIBUTION DESCRIPTION PAGE 1 A. Korkunov Korkunov chocolate bars Russia Milk and dark chocolate bars, plain, or with almonds or hazelnuts A. Loacker Co. Gardena Chocolate-orange or hazelnut cream filling in wafers covered with milk chocolate Adams and Brooks Cup-o-Gold United States Chocolate cup with a marshmallow center with almonds and coconut Ambrosoli Orly Chile Milk chocolate with fruit-flavoured creamy filling Anand Mills Union Amul Chocolate India Available in orange, milk and chocolate flavors Limited,India Annabelle Candy Company Rocky Road United States Marshmallow topped with cashews and covered with chocolate Annabelle Candy Company U-No Bar United States Milk Chocolate truffle-like center, covered with Milk Chocolate and ground almonds Annie's candy manufacturing Hany Milk Chocolate Philippines A soft milk chocolate bar Brockmann's Chocolates Inc Truffini Delta,B.C.,Canada All-natural, non-hydrogenated oils, filled truffle Brown and Haley Mountain Bar United States Vanilla, cherry, or peanut butter creme filling, covered in chocolate and peanuts in the shape of Mount Rainier Cachet India Sklofts India 5 sections: chocolate coated almonds, hazelnuts, raisins, butterscotch, cranberries Cadbury Top Deck South Africa White chocolate peaks layered on top of a milk chocolate base CAMPCO Chocolate Factory Turbo India Noughat Filled Creamy Chocolate Cavalier Woodies Belgium Milk chocolate bar with hazelnut or orange filling and a biscuit Chicken Ltd Ashmelia Ukraine Chocolate with kiwi flavoring Chocoworks Chocoelf Singapore More than 50 types of sugar-free and no Sugar-added chocolate bars Cocoa Processing Co. -

Preliminary Modelling and Mapping of Critical Loads for Cadmium and Lead in Europe
Working Group on Effects of the wge Convention on Long-range Transboundary Air Pollution RIVM reportno. 259101011/2002 Preliminary modelling and mapping of critical loads for cadmium and lead in Europe J.-P. Hettelingh, J. Slootweg, M. Posch (eds.) S. Dutchak, I. Ilyin (EMEP/MSC-E) Working Group on Effects of the wge Convention on Long-range Transboundary Air Pollution ICP M&M Coordination Center for Effects EMEP – Meteorological Synthesizing Centre - East page 2 Preliminary modelling and mapping of critical loads for cadmium and lead in Europe This investigation has been performed by order and for the account of the Directorate for Climate Change and Industry of the Dutch Ministry of Housing, Spatial Planning and the Environment within the framework of RIVM-project M259101, “UNECE-LRTAP”; and for the account of the Working Group on Effects within the trustfund for the partial funding of effect oriented activities under the Convention. RIVM, P.O. Box 1, 3720 BA Bilthoven, telephone: 31 - 30 - 274 91 11; telefax: 31 - 30 - 274 29 71 Preliminary modelling and mapping of critical loads for cadmium and lead in Europe page 3 Table of Contents Acknowledgements 5 Preface 6 Summary 8 Samenvatting (Summary in Dutch) 9 PART I Modelling and Mapping of Critical Loads for Cadmium and Lead 10 1. Preliminary Modelling and Mapping of Critical Loads for Cadmium and Lead and their Exceedances – Executive Summary 11 1.1 Introduction 11 1.2 Preliminary critical load results 12 1.3 Preliminary exceedance computation results 14 1.4 Recommendations 16 References 16 2. Guidance for the Calculation of Critical Loads for Cadmium and Lead in Terrestrial and Aquatic Ecosystems 17 2.1 Background and aim 17 2.2 Terrestrial ecosystems 19 2.3 Aquatic ecosystems 28 2.4 Summary of the present approach 32 2.5 Limitations in the present approach and possible future refinements 33 References 33 Appendix 1: Relations between cadmium and lead contents in soils extractable by aqua regia and total contents determined by HF extraction or x-ray fluorescence analysis 35 3. -

Minnesota Revenue Notice
Minnesota revenue notice Revenue Notice # 92-09 Sales and Use Tax - Application to Candy and Soft Drinks (Update: Revenue Notice #92-09 has been revoked by Revenue Notice #99-12.) Candy and soft drinks are subject to Minnesota sales and use tax. 1. Candy and Candy Products Products that are commonly packaged and sold as candy, including health and diet food products, are subject to sales tax whether sold over the counter or in a vending machine. Fruit, nuts, or popcorn which are combined with chocolate, carob, sugar, honey, candy, or other natural or artificial sweeteners are also considered candy and are subject to sales tax. Individually wrapped items ordinarily considered to be candy, such as Twix bars and PB Max bars, are taxable whether sold individually, in quantity, or in the candy or cookie sections. The following are examples of candy subject to sales tax. Brand names are specified only to illustrate types of items considered to be candy. they do not imply that these are the only taxable brands in any category. breath mints, including sugarless candy bars caramel corn caramel apples chocolate- or carob-covered nuts, raisins, etc. chocolate-covered insects chocolate stars cough drops (taxable as health product) Cracker Jack Crunch and Munch Fiddle Faddle honey-covered nuts licorice nature snacks with 50% or more candy peanut brittle sugarless candy throat lozenges (taxable as health product) yogurt-covered raisins, nuts, etc. fresh prepared popcorn sold by a vendor Products that are commonly sold as ingredients for cooking or baking purposes or as a meal substitute, e.g., breakfast bars, are not candy products and are exempt from tax.