DOCSLIB.ORG

Download Article (PDF)

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Download Article (PDF) Advances in Computer Science Research (ACSR), volume 76 7th International Conference on Education, Management, Information and Mechanical Engineering (EMIM 2017) Satellite Attitude Control with Actuator Failure Haitao Meng1,a, Aihua Zhang1,b, Xing Huo1,c and Zhiyong She2,d 1College of Engineering, Bohai University, Jinzhou 121013, China 2 China Beijing Aerospace Technology Institute [email protected], [email protected],[email protected], [email protected] Keywords: Observer; Backstepping; Actuator fault; Attitude stabilization control Abstract. A method of attitude stabilization control, based on observer design is proposed for an on-orbiting spacecraft in the presence of partial loss of actuator effectiveness, external disturbance and actuator control input saturation problem. In this approach, observer is employed to estimate the value of actuator fault, and a Backstepping attitude controller is then designed to achieve fault tolerant control and external disturbance rejection. The Lyapunov stability analysis shows that the closed-loop attitude system is guaranteed to be almost asymptotically stable. The simulation results show the effectiveness of the derived control law. Introduction It is inevitable that the satellite components is in trouble, so it is one of the hot spots in the research of attitude control to design the control algorithm to achieve the fault tolerant control. A spacecraft attitude compensation controller is designed using adaptive control method in literature [13]. In literature [14], a fault tolerant attitude control strategy is proposed for the non singular terminal sliding mode control method. In literature [9], a passive fault tolerant controller is designed based on time delay method. The attitude tracking control can be realized in the case of 4 flywheels, but the controller must obtain the fault information of the actuators. Application of two stage Kalman filtering algorithm in literature [11]. The Backstepping control method has many advantages such as the decomposition of the complex nonlinear system into many subsystems and the simple design procedure of the controller. Therefore the backstepping can be used to design the attitude controller. Considering the problem of actuator failure, external disturbance and actuator control input constraint in this paper, a method of attitude stabilization control is proposed to achieve high precision and high stability attitude stabilization control. Mathematical Model of the Satellite For description method using Euler angles of satellite attitude exists the singular problems, this paper adopts MRPs describe the satellite attitude, and then the rigid satellite attitude mathematical model can be described by: 1 Τ × Τ σɺ =()1 − σ σI + 2 σ + 2 σ σ ω 4 3 = F ()σ ω (1) × Jωɺ + ω J ω = τ + d (2) Τ ω=[ ω ω ω ] ∈ R3 where 1 2 3 is that coordinate system relative to the inertial coordinate system of Τ τ=[ τ τ τ ] ∈ R3 angular velocity to project on the body coordinate system, 1 2 3 is the total control Τ d=[ d d d] ∈ R3 moment that is actually applied to satellite coordinate system, 1 2 3 is external disturbs 3× 3 matrix of the satellite. Matrix JR∈ (positive definite and symmetric) is the moment of inertia of Copyright © 2017, the Authors. Published by Atlantis Press. 323 This is an open access article under the CC BY-NC license (http://creativecommons.org/licenses/by-nc/4.0/). Advances in Computer Science Research (ACSR), volume 76 the satellite array. In particular, Ep.(1) is the satellite attitude kinematics, and Ep. (2) is a rigid satellite attitude dynamics, and all of them is satisfied with Assumption 1. Assumption 1: Assumes that the external disturbance d is bounded, and there is constant d > 0 d≤ d max to make max to be established. Considering actuator partial failure and the fault is modeled as a multiplicative factor, so the actuator failure acting on the total control torque of the satellite ontology is as follows: τ= ρ τ ()t c (3) Τ τ= [ τ τ τ ] ∈ R3 where c c1 c 2 c 3 is actuator command control torque, ρ= [ ρ ρ ρ ]Τ ∈ 3× 3 ()()()()t diag( 1 t 2 t 3 t) R 0<ρ (), t ≤ 1 i = 1,2,3 is actuator fault degree, i , and where ρ ()t τ= τ i =1 and i ci , actuator normal operation and control torque is consistent with the actual torque; 0<ρ (t ) < 1 τ= ρ()t ρ < ρ If i , i i ci i , actuator partial failure. Controller Design In this approach, observer is employed to estimate the value of actuator faults, and a Backstepping attitude controller is then designed. ρ Observer Design. Because the fault factor ()t is a diagonal matrix, Eq. (3) can be rewritten by ρ τ= ρ ()()tc U t (4) Τ = [τ τ τ ] ∈ 3× 3 Τ U diag( c1()()() t c 2 t c 3 t) R ρ()()()()t= [ ρ t ρ t ρ t ] where , 1 2 3 , the satellite state dynamics Eq. (2) can be rewritten in the form of partial failure Eq.(3) ω= − ω× ω + ρ + Jɺ J U() t d (5) According to the attitude dynamics of spacecraft actuator fault Eq.(5), the design follows the ρ observer to estimate the fault ()t . ⌢ ⌢× ⌢ ⌢ Jωɺ = − ω J ω + U ρ() t ⌢ ⌢ −Γ()()ω − ω −l sng ω − ω 1 (6) ⌢ ⌢ ⌢ ρ()()t= l ρ t − Τ + l ( ω − ω) 2 3 (7) ⌢ ρ⌢ ρ whereω and ()t are the respectively estimated value of ω and ()t .Τ ∈ R is the update time of 3× 3 l∈ R the observer. Γ ∈ R , i + is Observer gain. In order to evaluate the performance of the observer I Eq.(6) - Eq.(7) fault estimation, the energy index p is defined. 1 t 2 2 I= e + σ dt p ∫ t 0 (8) τ≤ τ Attitude Stabilization Controller Design. When i max (i=1, 2, 3), application of observer ρ Eq.(6) - Eq.(7) can realize the accurate estimation of the failurepart ()t . = σ x1 dt x = σ x = ω Variable ∫ , 2 and 3 . According to Eq.(1) and Eq.(5), there are 324 Advances in Computer Science Research (ACSR), volume 76 xɺ = x 1 2 (9) xɺ = F() x x 2 2 3 (10) × ⌢ ⌢ Jxɺ = − x Jx +ρ()() t τ − δ t τ + d 3 3 3 c c (11) ⌢ ρ⌢= [] ρ ⌢ ρ ⌢ ρ ⌢ Τ δ= [] δ δ δ Τ where ()t diag ( 1 2 3 ) ， ()t diag ( 1 2 3 ). From the Eq.(9) to Eq.(11) shown in the form of the system structure, the standard Backstepping method can be used to design the controller. To carry out the following transformation z= x z = x −α z = x − α 1 1 2 2 1 3 3 2 (12) α ∈ R3 α ∈ R3 Where 1 and 2 are the virtual control inputs for backstepping control. The following steps can be divided into the controller design Step 1: According to the formula Eq.(12), available zɺ = xɺ = x = z + α 1 1 2 2 1 (13) V= 0.5 zΤ z Selected Lyapunov candidate function 1 1 1 and design the virtual control Variable .where α = −c x c 1 1 1 and where 1 is constant. Vzzzzczɺ =ΤΤɺ =() − = − cz2 + zzΤ 1111211 11 12 (14) 2 z = 0 Vɺ = − c z z So when 2 , 1 1 1 , 1 will be at the asymptotic convergence. z Step 2: according to the type of 2 derivative Eq.(16) available. zɺ = xɺ −αɺ = F() x x + c x 2 2 1 2 3 1 2 (15) V= V + 0.5 zΤ z α Select another Lyapunov function 2 1 2 2 and 2 for the design of virtual control input. α =F−1() x( − z − c x − c z ) 2 2 1 1 2 2 2 (16) c Where 2 is constant. Apply (16), there are ɺ = −2 +ΤΤ + [ + ] V2 cz 1 1 zzzFxxcx 1 2 2() 2 3 1 2 = −c z2 − c z2 + zΤ F() x x 1 1 2 2 2 2 3 (17) 2 2 z = 0 Vɺ = − c z − c z The same type from Eq.(17) to prove that when 3 , 2 1 1 1 1 . At this z z time 1 and 2 will converge. Aiming at the fault spacecraft attitude control system Eq.(1), Eq.(5), the application of observer Eq.(6) design command control: τ= Sat( v, τ ) c max (18) τ ∈ 3 The controller c input v R is designed as 325 Advances in Computer Science Research (ACSR), volume 76 −1 ⌢ − dF() x = ρ 1 2 ( + + ) v() t()[ t J z1 c 1 x 2 c 2 z 2 dt +−1 ( + + ) F() x2 zɺ 1 c 1 xɺ 2 c 2 zɺ 2 ] +× − − − Τ x3 Jx 3 c 3 z 3 k 1 xa F() x2 z 2 χ 2 zɺ − Τd 3 } χz + εexp( − βt ) Τd 3 (19) χ= τ + d ε ∈ R k∈ R β c Where Τd max max , + is an arbitrary small constant. 1 + , and 3 for control gain, x∈ R a + is the state variable of the following auxiliary system. ρ⌢ 2∆ 2 = − − ()t u −ρ⌢ ∆ xɺa k2 xa xa () t u x 2 a (20) ∆u =τ − v k∈ R c , 2 + . If 2 − > −k1 −1 > c31 0, k 2 0 2 2 (21) The whole closed-loop attitude control system is stable. Prove: By Eq.(11) and Eq.(16) available =−1 − × +ρ τ + zɺ3 J x 3 Jx 3 () tc d dF−1() x + 2 (z+ c x + c z ) dt 1 1 2 2 2 +F−1() x( zɺ + c xɺ + cz ɺ ) 2 1 1 2 2 2 (22) If a Lyapunov candidate function is defined = +1Τ + 1 Τ V3 V 2 z 3 Jz 3 xa x a 2 2 (23) The function of the time derivative of V3, and put Eq.(22) into ɺ = −2 −2 −2 − 2 V3 c 1 z 1 c 2 z 2 c 3 z 3 k 2 xa −ρ⌢ 2 ∆ 2 −Τρ⌢ ∆ ()t u xa () t u ⌢ +Τ ρ⌢ ∆ − − δ τ z3{() t u k 1 xa () t c z χ 2 +d − 3 Τd } zχ+ εexp( − β t ) 3 Τd (24) ⌢ −δ()t τ + d ≤ τ + d According to the characteristic of saturation function, c max max .
Load more

Recommended publications
  • Classlists for C by Group
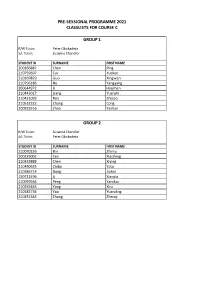
    PRE-SESSIONAL PROGRAMME 2021 CLASSLISTS FOR COURSE C GROUP 1 R/W Tutor: Peter Obukadeta S/L Tutor: Suzanne Chandler STUDENT ID SURNAME FIRST NAME 200166887 Chen Ping 210759697 Cui Yuekun 210169829 Guo Xingwen 210796186 Hu Yangyang 200644972 Li Haozhan 210443017 Liang Yuanzhi 210421093 Ren Zhijiao 210532322 Zhang Cong 200925516 Zhao Yashan GROUP 2 R/W Tutor: Suzanne Chandler S/L Tutor: Peter Obukadeta STUDENT ID SURNAME FIRST NAME 210070226 Bin Zhimu 200329002 Cen Xiaofeng 210333888 Chen Xiying 210450635 Chiba Yota 210386714 Dong Jiahui 190711496 Li Xiaoxia 210059564 Peng Yanduo 210255465 Yang Xiru 210182736 Yao Yuanding 210252383 Zhang Zhenqi GROUP 3 R/W Tutor: Mark Heffernan S/L Tutor: Alan Hart STUDENT ID SURNAME FIRST NAME 210154386 Cai Zhenping 210462580 Ge Xiaodan 210648276 Hirunkhajonrote Kullanut 210182714 Huang Siwei 200141563 Kung Tzu-Ning 200305176 Punsri Punnatorn 200664774 Sayin Humeyra 210186446 Shehata Omar 171003323 Tutberidze Tea 200134624 Wang Shuo 200136019 Xu Ming 200278696 Yan Jiaxin 210357851 Yuan Lai 210029165 Zhang Anru 210219777 Zhang Jiasheng GROUP 4 R/W Tutor: Sherin White S/L Tutor: Alan Hart STUDENT ID SURNAME FIRST NAME 200247588 Chen Chong 200349343 Li Cheng 210622933 Liang Wenxuan 210219618 Liu Huiyuan 210376298 Liu Zeyu 210237531 Mei Lyuke 200132620 Qi Shuyu 210681907 Wang Handuo 200015356 Wu Zhuoyue 200071994 Xie Kaijun GROUP 5 R/W Tutor: Chukwudi Dozie S/L Tutor: Nora Mikso STUDENT ID SURNAME FIRST NAME 210563304 Almalek Ahmed 210186309 Altamimi Saud 210251102 Cheng Han-Yu 210349823 Guo Wenyuan 210239409
    [Show full text]
  • Electronic Supplementary Information
    Electronic Supplementary Material (ESI) for RSC Advances. This journal is © The Royal Society of Chemistry 2014 Electronic Supplementary Information A Facile Green One-pot Route Towards Three-Dimensional Graphene- Based micropores carbon composites Frameworks for High-Performance Electrochemical Capacitive Energy Storage Zehui Zhang, Peiyi Wu * State Key Laboratory of Molecular Engineering of Polymers and Department of Macromolecular Science and Laboratory of Advanced Materials, Fudan University, Shanghai 200433, P.R. China E-mail: [email protected]. Figure S1. Digital photographs of the samples. Figure S2. Isotherm plot of NC, GA-NC-0.5, GA-NC-1, GA-NC-1.5. Figure S3. Pore size distribution plots obtained using the DFT method of the GA-NC- 1. Figure S4. Elemental mapping images of GA-AC-1. (a) EDX spectrum suggest the homogeneous distribution of N and C in GA-AC-1. (b) Typical scanning electron microscopy image and corresponding elemental mapping images of (c) nitrogen and (d) carbon in the selected area. Table S1. Element analysis of the chiotsan and GA-NC. The increase of carbon content indicates the sufficient carbonization during the high temperature treatment. Sample C (%) H (%) N (%) O (Calculated) (%) chiotsan 41.33 7.95 7.78 42.84 GA-NC 74.65 1.67 6.30 17.38 Figure S5. Raman spectra of GA-NC. Figure S6. FTIR spectrum of GA-NC. Figure S7. a)，c), e) Cyclic voltammetry curves obtained at different scan rates for NC, GA-NC-0.5, GA-NC-1.5, respectively. b), d), f) Galvanostatic charge/discharge curves of NC, GA-NC-0.5, GA-NC-1.5 supercapacitor under different constant currents, respectively.
    [Show full text]
  • French Names Noeline Bridge
    names collated:Chinese personal names and 100 surnames.qxd 29/09/2006 13:00 Page 8 The hundred surnames Pinyin Hanzi (simplified) Wade Giles Other forms Well-known names Pinyin Hanzi (simplified) Wade Giles Other forms Well-known names Zang Tsang Zang Lin Zhu Chu Gee Zhu Yuanzhang, Zhu Xi Zeng Tseng Tsang, Zeng Cai, Zeng Gong Zhu Chu Zhu Danian Dong, Zhu Chu Zhu Zhishan, Zhu Weihao Jeng Zhu Chu Zhu jin, Zhu Sheng Zha Cha Zha Yihuang, Zhuang Chuang Zhuang Zhou, Zhuang Zi Zha Shenxing Zhuansun Chuansun Zhuansun Shi Zhai Chai Zhai Jin, Zhai Shan Zhuge Chuko Zhuge Liang, Zhan Chan Zhan Ruoshui Zhuge Kongming Zhan Chan Chaim Zhan Xiyuan Zhuo Cho Zhuo Mao Zhang Chang Zhang Yuxi Zi Tzu Zi Rudao Zhang Chang Cheung, Zhang Heng, Ziche Tzuch’e Ziche Zhongxing Chiang Zhang Chunqiao Zong Tsung Tsung, Zong Xihua, Zhang Chang Zhang Shengyi, Dung Zong Yuanding Zhang Xuecheng Zongzheng Tsungcheng Zongzheng Zhensun Zhangsun Changsun Zhangsun Wuji Zou Tsou Zou Yang, Zou Liang, Zhao Chao Chew, Zhao Kuangyin, Zou Yan Chieu, Zhao Mingcheng Zu Tsu Zu Chongzhi Chiu Zuo Tso Zuo Si Zhen Chen Zhen Hui, Zhen Yong Zuoqiu Tsoch’iu Zuoqiu Ming Zheng Cheng Cheng, Zheng Qiao, Zheng He, Chung Zheng Banqiao The hundred surnames is one of the most popular reference Zhi Chih Zhi Dake, Zhi Shucai sources for the Han surnames. It was originally compiled by an Zhong Chung Zhong Heqing unknown author in the 10th century and later recompiled many Zhong Chung Zhong Shensi times. The current widely used version includes 503 surnames. Zhong Chung Zhong Sicheng, Zhong Xing The Pinyin index of the 503 Chinese surnames provides an access Zhongli Chungli Zhongli Zi to this great work for Western people.
    [Show full text]
  • Is Shuma the Chinese Analog of Soma/Haoma? a Study of Early Contacts Between Indo-Iranians and Chinese
    SINO-PLATONIC PAPERS Number 216 October, 2011 Is Shuma the Chinese Analog of Soma/Haoma? A Study of Early Contacts between Indo-Iranians and Chinese by ZHANG He Victor H. Mair, Editor Sino-Platonic Papers Department of East Asian Languages and Civilizations University of Pennsylvania Philadelphia, PA 19104-6305 USA [email protected] www.sino-platonic.org SINO-PLATONIC PAPERS FOUNDED 1986 Editor-in-Chief VICTOR H. MAIR Associate Editors PAULA ROBERTS MARK SWOFFORD ISSN 2157-9679 (print) 2157-9687 (online) SINO-PLATONIC PAPERS is an occasional series dedicated to making available to specialists and the interested public the results of research that, because of its unconventional or controversial nature, might otherwise go unpublished. The editor-in-chief actively encourages younger, not yet well established, scholars and independent authors to submit manuscripts for consideration. Contributions in any of the major scholarly languages of the world, including romanized modern standard Mandarin (MSM) and Japanese, are acceptable. In special circumstances, papers written in one of the Sinitic topolects (fangyan) may be considered for publication. Although the chief focus of Sino-Platonic Papers is on the intercultural relations of China with other peoples, challenging and creative studies on a wide variety of philological subjects will be entertained. This series is not the place for safe, sober, and stodgy presentations. Sino- Platonic Papers prefers lively work that, while taking reasonable risks to advance the field, capitalizes on brilliant new insights into the development of civilization. Submissions are regularly sent out to be refereed, and extensive editorial suggestions for revision may be offered. Sino-Platonic Papers emphasizes substance over form.
    [Show full text]
  • Gateless Gate Has Become Common in English, Some Have Criticized This Translation As Unfaithful to the Original
    Wú Mén Guān The Barrier That Has No Gate Original Collection in Chinese by Chán Master Wúmén Huìkāi (1183-1260) Questions and Additional Comments by Sŏn Master Sǔngan Compiled and Edited by Paul Dōch’ŏng Lynch, JDPSN Page ii Frontspiece “Wú Mén Guān” Facsimile of the Original Cover Page iii Page iv Wú Mén Guān The Barrier That Has No Gate Chán Master Wúmén Huìkāi (1183-1260) Questions and Additional Comments by Sŏn Master Sǔngan Compiled and Edited by Paul Dōch’ŏng Lynch, JDPSN Sixth Edition Before Thought Publications Huntington Beach, CA 2010 Page v BEFORE THOUGHT PUBLICATIONS HUNTINGTON BEACH, CA 92648 ALL RIGHTS RESERVED. COPYRIGHT © 2010 ENGLISH VERSION BY PAUL LYNCH, JDPSN NO PART OF THIS BOOK MAY BE REPRODUCED OR TRANSMITTED IN ANY FORM OR BY ANY MEANS, GRAPHIC, ELECTRONIC, OR MECHANICAL, INCLUDING PHOTOCOPYING, RECORDING, TAPING OR BY ANY INFORMATION STORAGE OR RETRIEVAL SYSTEM, WITHOUT THE PERMISSION IN WRITING FROM THE PUBLISHER. PRINTED IN THE UNITED STATES OF AMERICA BY LULU INCORPORATION, MORRISVILLE, NC, USA COVER PRINTED ON LAMINATED 100# ULTRA GLOSS COVER STOCK, DIGITAL COLOR SILK - C2S, 90 BRIGHT BOOK CONTENT PRINTED ON 24/60# CREAM TEXT, 90 GSM PAPER, USING 12 PT. GARAMOND FONT Page vi Dedication What are we in this cosmos? This ineffable question has haunted us since Buddha sat under the Bodhi Tree. I would like to gracefully thank the author, Chán Master Wúmén, for his grace and kindness by leaving us these wonderful teachings. I would also like to thank Chán Master Dàhuì for his ineptness in destroying all copies of this book; thankfully, Master Dàhuì missed a few so that now we can explore the teachings of his teacher.
    [Show full text]
  • Use Text Mining and Complex Networks to Analyze
    Advances in Biological Sciences Research (ABSR), volume 4 2nd International Conference on Biomedical and Biological Engineering 2017 (BBE 2017) Use Text Mining and Complex Networks to Analyze TCM Syndromes Xing ZHAI1,a,*, Ping WANG2 and You-liang HUANG3 1,2,3Beijing University of Chinese Medicine, 11 Bei San Huan Dong Lu, ChaoYang District, Beijing 100029,Peoples Republic of China [email protected] *Corresponding author Keywords: Text mining, Complex network, Traditional Chinese medicine. Abstract. Objective: To make intrinsic biological distinctions between qi deficiency pattern and qi stagnation pattern with genes related to NEI. Methods: Establish a data dictionary of NEI-related genes and a keyword lexicon of qi deficiency pattern and qi stagnation pattern. Then retrieve relevant literature on Pubmed database. Obtain compositions of characteristic NEI-related genes of qi deficiency pattern and qi stagnation pattern by using text-mining methodto explore different bioactive materials between the two syndromes. Results: Two kinds of syndromes and their biological networks were constructed. The "qi deficiency" and "qi stagnation" genes based on NEI network were excavated. Conclusion: The genes of qi stagnation pattern relate closely with nerve and endocrine, while those of qi deficiency pattern have a close relationship with the immune system. The intrinsic biological characterizations of TCM patterns can be effectively identified at the level of NEI. Introduction In the biomedical field, due to the abrupt growth of the number ofbiological data and biomedical literature, to finding out regulars and new achievements through data mining have become a new hot spot and an important branch of biological study [1]. Text Mining is a specific research area ofthe interdisciplinary subject, data mining.
    [Show full text]
  • Cha Zhang, Chang−Shui Zhang, Chengcui Zhang, Dengsheng Zhang, Dong Zhang, Dongming Zhang, Hong−Jiang Zhang, Jiang Zhang, Jianning Zhang, Keqi Zhang, Lei Zhang, Li
    Z Zeng, Wenjun Zeng, Zhihong Zhai, Yun Zhang, Benyu Zhang, Cha Zhang, Chang−Shui Zhang, Chengcui Zhang, Dengsheng Zhang, Dong Zhang, Dongming Zhang, Hong−Jiang Zhang, Jiang Zhang, Jianning Zhang, Keqi Zhang, Lei Zhang, Li Menu Next Z Zhang, Like Zhang, Meng Zhang, Mingju Zhang, Rong Zhang, Ruofei Zhang, Weigang Zhang, Yongdong Zhang, Yun−Gang Zhang, Zhengyou Zhang, Zhenping Zhang, Zhenqiu Zhang, Zhishou Zhang, Zhongfei (Mark) Zhao, Frank Zhao, Li Zhao, Na Prev Menu Next Z Zheng, Changxi Zheng, Yizhan Zhi, Yang Zhong, Yuzhuo Zhou, Jin Zhu, Jiajun Zhu, Xiaoqing Zhu, Yongwei Zhuang, Yueting Zimmerman, John Zoric, Goranka Zou, Dekun Prev Menu Wenjun Zeng Organization : University of Missouri−Columbia, United States of America Paper(s) : ON THE RATE−DISTORTION PERFORMANCE OF DYNAMIC BITSTREAM SWITCHING MECHANISMS (Abstract) Letter−Z Menu Zhihong Zeng Organization : University of Illinois at Urbana−Champaign, United States of America Paper(s) : AUDIO−VISUAL AFFECT RECOGNITION IN ACTIVATION−EVALUATION SPACE (Abstract) Letter−Z Menu Yun Zhai Organization : University of Central Florida, United States of America Paper(s) : AUTOMATIC SEGMENTATION OF HOME VIDEOS (Abstract) Letter−Z Menu Benyu Zhang Organization : Microsoft Research Asia, China Paper(s) : SUPERVISED SEMI−DEFINITE EMBEDING FOR IMAGE MANIFOLDS (Abstract) Letter−Z Menu Cha Zhang Organization : Microsoft Research, United States of America Paper(s) : HYBRID SPEAKER TRACKING IN AN AUTOMATED LECTURE ROOM (Abstract) Letter−Z Menu Chang−Shui Zhang Organization : Tsinghua University, China
    [Show full text]
  • Social Mobility in China, 1645-2012: a Surname Study Yu (Max) Hao and Gregory Clark, University of California, Davis [email protected], [email protected] 11/6/2012
    Social Mobility in China, 1645-2012: A Surname Study Yu (Max) Hao and Gregory Clark, University of California, Davis [email protected], [email protected] 11/6/2012 The dragon begets dragon, the phoenix begets phoenix, and the son of the rat digs holes in the ground (traditional saying). This paper estimates the rate of intergenerational social mobility in Late Imperial, Republican and Communist China by examining the changing social status of originally elite surnames over time. It finds much lower rates of mobility in all eras than previous studies have suggested, though there is some increase in mobility in the Republican and Communist eras. But even in the Communist era social mobility rates are much lower than are conventionally estimated for China, Scandinavia, the UK or USA. These findings are consistent with the hypotheses of Campbell and Lee (2011) of the importance of kin networks in the intergenerational transmission of status. But we argue more likely it reflects mainly a systematic tendency of standard mobility studies to overestimate rates of social mobility. This paper estimates intergenerational social mobility rates in China across three eras: the Late Imperial Era, 1644-1911, the Republican Era, 1912-49 and the Communist Era, 1949-2012. Was the economic stagnation of the late Qing era associated with low intergenerational mobility rates? Did the short lived Republic achieve greater social mobility after the demise of the centuries long Imperial exam system, and the creation of modern Westernized education? The exam system was abolished in 1905, just before the advent of the Republic. Exam titles brought high status, but taking the traditional exams required huge investment in a form of “human capital” that was unsuitable to modern growth (Yuchtman 2010).
    [Show full text]
  • Self-Study Syllabus on Chinese Foreign Policy
    Self-Study Syllabus on Chinese Foreign Policy www.mandarinsociety.org PrefaceAbout this syllabus with China’s rapid economic policymakers in Washington, Tokyo, Canberra as the scale and scope of China’s current growth, increasing military and other capitals think about responding to involvement in Africa, China’s first overseas power,Along and expanding influence, Chinese the challenge of China’s rising power. military facility in Djibouti, or Beijing’s foreign policy is becoming a more salient establishment of the Asian Infrastructure concern for the United States, its allies This syllabus is organized to build Investment Bank (AIIB). One of the challenges and partners, and other countries in Asia understanding of Chinese foreign policy in that this has created for observers of China’s and around the world. As China’s interests a step-by-step fashion based on one hour foreign policy is that so much is going on become increasingly global, China is of reading five nights a week for four weeks. every day it is no longer possible to find transitioning from a foreign policy that was In total, the key readings add up to roughly one book on Chinese foreign policy that once concerned principally with dealing 800 pages, rarely more than 40–50 pages will provide a clear-eyed assessment of with the superpowers, protecting China’s for a night. We assume no prior knowledge everything that a China analyst should know. regional interests, and positioning China of Chinese foreign policy, only an interest in as a champion of developing countries, to developing a clearer sense of how China is To understanding China’s diplomatic history one with a more varied and global agenda.
    [Show full text]
  • Lǎoshī Hé Xuéshēng (Teacher and Students)
    © Copyright, Princeton University Press. No part of this book may be distributed, posted, or reproduced in any form by digital or mechanical means without prior written permission of the publisher. CHAPTER Lǎoshī hé Xuéshēng 1 (Teacher and Students) Pinyin Text English Translation (A—Dīng Yī, B—Wáng Èr, C—Zhāng Sān) (A—Ding Yi, B—Wang Er, C—Zhang San) A: Nínhǎo, nín guìxìng? A: Hello, what is your honorable surname? B: Wǒ xìng Wáng, jiào Wáng Èr. Wǒ shì B: My surname is Wang. I am called Wang Er. lǎoshī. Nǐ xìng shénme? I am a teacher. What is your last name? A: Wǒ xìng Dīng, wǒde míngzi jiào Dīng Yī. A: My last name is Ding and my full name is Wǒ shì xuéshēng. Ding Yi. I am a student. 老师 老師 lǎoshī n. teacher 和 hé conj. and 学生 學生 xuéshēng n. student 您 nín pron. honorific form of singular you 好 hǎo adj. good 你(您)好 nǐ(nín)hǎo greeting hello 贵 貴 guì adj. honorable 贵姓 貴姓 guìxìng n./v. honorable surname (is) 我 wǒ pron. I; me 姓 xìng n./v. last name; have the last name of … 王 Wáng n. last name Wang 叫 jiào v. to be called 二 èr num. two (used when counting; here used as a name) 是 shì v. to be (any form of “to be”) 10 © Copyright, Princeton University Press. No part of this book may be distributed, posted, or reproduced in any form by digital or mechanical means without prior written permission of the publisher.
    [Show full text]
  • BIOGRAPHICAL SKETCH NAME: Jianhua Zhang Era
    OMB No. 0925-0001/0002 (Rev. 08/12 Approved Through 8/31/2015) BIOGRAPHICAL SKETCH Provide the following information for the Senior/key personnel and other significant contributors. Follow this format for each person. DO NOT EXCEED FIVE PAGES. NAME: Jianhua Zhang eRA COMMONS USER NAME (credential, e.g., agency login): JZHANG123 POSITION TITLE: Associate Professor EDUCATION/TRAINING (Begin with baccalaureate or other initial professional education, such as nursing, include postdoctoral training and residency training if applicable. Add/delete rows as necessary.) DEGREE Completion (if Date FIELD OF STUDY INSTITUTION AND LOCATION applicable) MM/YYYY University of Science & Technology of China B.S. 1984 Biology University of Texas Southwestern Medical Center Ph.D. 1991 Cell & Molecular Biology Whitehead Institute for Biomedical Research Postdoc 1995 Molecular Biology A. Personal statement I came to the US in 1985 via a CUSPEA program, trained with Dr. Joseph Sambrook at UT Southwestern on molecular cloning and cellular retinoic acid binding protein structure/function relationships, and from 1991 to 1995 with Dr. Rick Young in the Whitehead Institute on the genetics of RNA polymerase holoenzyme and coactivator functions. From 1996 to 2005 I had been working with genetically engineered mouse models of (i) dopamine receptors, (ii) immediate early gene transcription factor c-fos, and (iii) DNA fragmentation factors in neuroplasticity and apoptosis at the Univ of Cincinnati, by generating and analyzing conventional and conditional mouse knockout and transgenic models. In 2005 I became a tenure track assistant professor in UAB where I focused my research program on how the autophagy-lysosomal pathway plays a role in neuronal function and survival, in the context of Parkinson’s disease.
    [Show full text]
  • Scott J. Brandenberg, Jian Zhang, Yili Huo, and Minxing Zhao, UCLA
    Simulation of 3-D Global Bridge Response to Shaking and Lateral Spreading Scott J. Brandenberg, Jian Zhang, Yili Huo, and Minxing Zhao, UCLA PEER Transportation Systems Research Program May 2, 2011 Project Description PEER Transportation Systems Research Program 2/14 1-D site response analyses • Ground Motion Records from 2007 Niigata Earthquake • Records from Centrifuge Test PEER Transportation Systems Research Program 3/14 1-D site response analyses • Records from Numerical Simulation 10 with dilatancy ) 2 5 0 -5 Acceleration (m/s Acceleration Ground surface motion -10 0 10 20 30 Time (second) 1 0.5 0 -0.5 in loose sand -1 Excess Pore Pressure Ratio Pressure Pore Excess 0 10 20 30 Time (second) 10 ) 2 5 0 -5 Acceleration (m/s Acceleration Base input motion No.35 -10 0 10 20 30 Time (second) A liquefied sand layer is not a “base isolator”. PEER Transportation Systems Research Program 4/14 1-D site response analyses • Site Amplification Factor – Baseline Soil Profile liq.liq. noliq.noliq. 10 10 ) ) 2 2 s / s / m m ( ( liq noliq a 1 a 1 S S 0.1 0.1 0.01 0.1 1 10 0.01 0.1 1 10 Period (second) Period (second) = Fa Sa liq/ Sa noliq a 1 1 a F Median of F of Median median curve 0.1 0.01 0.1 1 10 0.01 0.1 1 10 Period (second) Period (second) PEER Transportation Systems Research Program 5/14 1-D site response analyses • Site Amplification Factor – Monte Carlo Simulations a F 1 f o n a i d e M 0.01 0.1 1 10 Period (second) PEER Transportation Systems Research Program 6/14 Modeling of the studied case 6 6 3 3 Disp (m) Disp (m) Disp(m) Disp (m) 0 1 2 0 1 2 -2 -1 0 -2 -1 0 0 0 0 0 7s Bridge and soil layer sketch Depth(m) 14s (m) Depth -3 -3 -3 21s -3 28s 35s -6 -6 (m) Depth -6 Depth(m) 42s -6 49s 56s -9 -9 -9 63s -9 70s Soil layer simplification (a) Left abut (b) Left pier (c) Right pier (d) Right abut Longitudinal displacement profiles with motion No.
    [Show full text]