Hidden Beauty in Twisted Viking Neck Rings
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

New Concept for Museum Storage Buildings – Evaluation of Building Performance Model for Simulation of Storage
Downloaded from orbit.dtu.dk on: Sep 30, 2021 New Concept for Museum Storage Buildings – Evaluation of Building Performance Model for Simulation of Storage Christensen, Jørgen Erik; Knudsen, Lise Ræder ; Kollias, Christos Georgios Published in: 2016 International Conference on Architecture and Civil Engineering. Publication date: 2016 Document Version Peer reviewed version Link back to DTU Orbit Citation (APA): Christensen, J. E., Knudsen, L. R., & Kollias, C. G. (2016). New Concept for Museum Storage Buildings – Evaluation of Building Performance Model for Simulation of Storage. In 2016 International Conference on Architecture and Civil Engineering. International Conference on Architecture and Civil Engineering. Annual Proceedings General rights Copyright and moral rights for the publications made accessible in the public portal are retained by the authors and/or other copyright owners and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights. Users may download and print one copy of any publication from the public portal for the purpose of private study or research. You may not further distribute the material or use it for any profit-making activity or commercial gain You may freely distribute the URL identifying the publication in the public portal If you believe that this document breaches copyright please contact us providing details, and we will remove access to the work immediately and investigate your claim. New Concept for Museum Storage Buildings Evaluation -

Plastic at Recycling Centres, Background Background Report, Phase 1
Ved Stranden 18 DK-1061 Copenhagen K www.norden.org NORDISKE ARBEJDSPAPIRER N ORDIC W ORKING P APERS Plastic at Recycling Centres, Background Background report, phase 1 http://dx.doi.org/10.6027/NA2014-912 NA2014:912 ISSN 2311-0562 This working paper has been published with financial support from the Nordic Council of Ministers. However, the contents of this working paper do not necessarily reflect the views, policies or recommendations of the Nordic Council of Ministers. FEBRUARY 2014 NORDIC COUNCIL OF MINISTERS Plastic at Recycling Centres, Background BACKGROUND REPORT, PHASE 1 ADDRESS COWI A/S Parallelvej 2 2800 Kongens Lyngby Denmark TEL +45 56 40 00 00 FAX +45 56 40 99 99 WWW cowi.com FEBRUARY 2014 NORDIC COUNCIL OF MINISTERS Plastic at Recycling Centres, Background BACKGROUND REPORT, PHASE 1 PROJECT NO. A039775 DOCUMENT NO. A039775-101 VERSION 02 DATE OF ISSUE February 2014 PREPARED ASWE CHECKED LISA APPROVED LISA Background Report for Guide for Plastic Sorting at Recycling Centres 5 CONTENTS 1 Summary 7 2 Resume (in Danish) 8 3 Introduction 9 4 Methodology for the development of the guideline 11 4.1 Reference group 11 4.2 Collection of published data 11 4.3 Interviews 12 4.4 Workshop 12 4.5 Assessment of data from stakeholders and projects 13 5 Information on existing systems 14 5.1 Amounts 14 5.2 Plastic waste based on applications and post- consumer waste streams 14 5.3 Collection systems at the recycling centres 16 5.4 Synergy with other local systems 20 5.5 Handling plastic containing hazardous substances 21 5.6 Transport costs -

Landsdækkende Screening Af Geotermi I 28 Fjernvarmeområder
Landsdækkende screening af geotermi i 28 fjernvarmeområder Bilag 3: Områderapport for Nykøbing Falster Indholdsfortegnelse – Introduktion – Data for fjernvarmeområder (COWI) – Beregning af geotermianlæg (DFG) – Beregningsresultater vedr. indpasning af geotermi (Ea) – Geologisk vurdering (GEUS) Introduktion Dette er én ud af 28 områderapporter, som viser specifikke økonomiske og produktionsmæssige resultater for hvert enkelt område. Rapporten er et bilag til hovedrapporten ”Landsdækkende screening af geotermi i 28 fjernvarmeområder”, og bør læses i sammenhæng med denne, da hovedrapporten indeholder information, der er væsentlig for at forstå resultatet. Rapporten er udarbejdet for Energistyrelsen af Dansk Fjernvarmes Geotermiselskab, COWI og Ea Energianalyse i perioden efteråret 2013 til sommeren 2015. Områderapporten indeholder den af GEUS udførte geologiske vurdering, COWIs beskrivelse af fjernvarmeområdet og den fremtidige forsyningsstruktur, Dansk Fjernvarmes Geotermiselskabs beregninger af de økonomiske og tekniske forhold i et geotermianlæg i fjernvarmeområdet, og Ea Energianalyses modelresultater fra Balmorel med varmeproduktionskapaciteter, fjernvarmeproduktion og -omkostninger over året for de fire scenarier i årene 2020, 2025 og 2035. Resultaterne skal tages med en række forbehold. Først og fremmest skal det understreges, at der er tale om en screening med det formål at give en indikation af mulighederne for geotermi. Der er ikke foretaget en fuldstændig analyse af den optimale fremtidige fjernvarmeforsyning i området. Den geologiske vurdering er alene foretaget for en enkelt lokalitet, svarende til en umiddelbart vurderet fordelagtig placering af geotermianlægget. Der kan derfor ikke drages konklusioner om hele områdets geologisk potentiale og den optimale placering for et eventuelt geotermianlæg. Modellering af områdets nuværende og forventede fremtidige fjernvarmeproduktion og -struktur er sket ud fra de data, som de var oplyst og forelå i år 2013. -

Page 1 P E R N I L L E
P E R N I L L E P O N T O P P I D A N P E D E R S E N Born in 1987 in Skive, Denmark Lives and work on a farm in the woods around Silkeborg, Denmark Pernille Pontoppidan Pedersen started her career as a ceramist by undermining the bases of this discipline. She developed an aesthetic of the ugly, the failure, the missed attempt. In one of her first series of work, she chose to disregard her training to excellence by integrating to her art the failed experiences of the best ceramic artists of the country. She Kills the jar, the pot, bowl and all the craft objects, to which ceramics limited itself for a long time. She undermines her discipline, and starts to reconstruct: shaky and almighty structures, tiered tempetto- pieces, sandcastles, heaps of found objects caught in a heavy flow of clay, foamy glazes that overflow like washing up fluid. The works of Pernille Pontoppidan tell a hundred pieces of fascinated stories superimposed in a cadaver exquis of good and very bad taste, of baroque and minimalism, of extreme dexterity and bitter failures. E D U C A T I O N 2012 BA in ceramics, Royal Danish Academy, School of Architecture, Design and Conservation, the school of design, Bornholm, Denmark E X H I B I T I O N S 2019 Chart Art fair, with Køppe Contemporary, Copenhagen Ceramic Momentum, group exhibition, CLAY Museum, Copenhagen 2018 Chart Art fair, with Køppe Contemporary, Copenhagen Dialogue through time, group exhibition, Wilds’sches Haus, Basel 2017 Beyond Icons, group exhibition, Koldinghus TRESOR Art Fair, with Køppe Contemporary, -

Lyngby Live Stream Online
1 / 3 Lyngby Live Stream Online Vejle vs Lyngby live stream on 24 May, 2021 all Live Streaming and TV Listings.. May 8, 2021 — 08.05.2021 Brugge vs Vikings (ESL B) Counter-Strike: Global Offensive Match. All EC Brugge Lyngby Vikings match info - livescore, results, .... With World Sports Betting you can place bets online for national and international ... Live stream Movistar Riders against Lyngby Vikings 〖 2021-03-29 〗 Watch .... Sep 28, 2019 — Listen to live radio, sports and News, online radio Denmark, Internet Radio ... Most music streaming apps require that we pay for the subscription fee just ... Hillerød, Hvidovre, Høje- Taastrup, Hørsholm, Ishøj, Lyngby-Taarbæk, .... Stream Sunday Night Football, the Premier League, the NHL, NASCAR, Cycling, the Kentucky Derby and more on NBC Sports, the NBC Sports app and NBC .... Lyngby vs. Aalborg Free Live Online Streaming Details. David Nielsen: It is a really good football game. Lyngby starts a busy football week when Monday puts .... Defeating Lyngby with a score of 2-1 on the opponent's field in the first leg, the Odense players took on more ... Jun 25, 2021 — Best of 3 (Online) * Swiss round 5 (teams with a 2-2 record). Winner advances to playoffs, losing team is eliminated. 1. Lyngby Vikings removed .... FeTiSh (Coach), Henrik Christensen, 2017-05-02, 2017-10-24, Lyngby Vikings (Coach). Denmark · valde, Valdemar Bjørn Vangså, 2016-08-26, 2017-05-21 .... Nov 9, 2008 — ... Forecasts Results Statistics Match details All the latest information about the match Watch results online ▷ fscore-bd.com.. Jan 23, 2021 — Live Stream ⋊ Lyngby Vikings x Sinners Esports ➦〖 2021-01-23 〗Watch CS:GO live score in the tournament - European Development ... -

Godkendte Uddannelser Til Optagelse I IDA Som Medlem
1 af 10 Godkendte uddannelser til optagelse i IDA som medlem Denne liste er baseret på KOT, Den Koordinerede tilmelding, fra Uddannelses- og Forskningsministeriet, som primært indeholder bacheloruddannelser. Medlemsberettigede kandidatuddannelser på https://ida.dk/bliv-medlem/hvem-kan-blive-ida-medlem. KOT-nr. Københavns Universitet 10117 Farmaci, København K, Studiestart: sommerstart 10140 Veterinærmedicin, København K, Studiestart: sommerstart 10150 Sundhed og informatik, København K, Studiestart: sommerstart 10205 Biokemi, København K, Studiestart: sommerstart 10218 Datalogi-økonomi, København K, Studiestart: sommerstart 10220 Datalogi, København K, Studiestart: sommerstart 10221 Forsikringsmatematik, København K, Studiestart: sommerstart 10230 Fysik, København K, Studiestart: sommerstart 10234 Bioteknologi, København K, Studiestart: sommerstart 10237 Husdyrvidenskab, København K, Studiestart: sommerstart 10238 Miljø- og fødevareøkonomi, Frederiksberg C, Studiestart: sommerstart 10240 Landskabsarkitektur, København K, Studiestart: sommerstart 10242 Fødevarer og ernæring, København K, Studiestart: sommerstart 10244 Naturressourcer, København K, Studiestart: sommerstart 10250 Biologi, København K, Studiestart: sommerstart 10270 Geografi og geoinformatik, København K, Studiestart: sommerstart 10275 Geologi-geoscience, København K, Studiestart: sommerstart 10285 Idræt og fysisk aktivitet, København K, Studiestart: sommerstart 10286 Kemi, København K, Studiestart: sommerstart 10287 Matematik, København K, Studiestart: sommerstart 10288 -

Horsens Biogasanlæg by & Bygning Arkitekter
HORSENS BIOGASANLÆG DISPOSITIONSFORSLAG 22. AUGUST 2012 Gottlieb Paludan + Public Arkitekter BY & BYGNING ARKITEKTER GOTTLIEB PALUDAN BY & BYGNING ARKITEKTER COWI A/S Kalvebod Brygge 30 Silstrupparken 2 Parallelvej 2 1560 København V 7700 Thisted 2800 Kongens Lyngby 02 BIOGASANLÆG, ARKITEKTUR OG LANDSKAB Som et led i at gøre den danske energiforsyning uafhængig Horsens Biogasanlæg er et af disse 7 pilotprojekter og vil med af fossile brændstoff er, vil biogas blive et vigtigt bidrag sin placering ved E45 blive et af de mest synlige biogasanlæg fremover. I de kommende år skal der etableres adskillige i Danmark. En placering, som derfor stiller særlige krav til en nye biogasanlæg i det åbne land og det er derfor vigtigt at velovervejet indpasning i det omkringliggende landskab. undersøge, hvordan disse nye tekniske byggerier vil påvirke det danske kulturlandskab. På nærværende projekt har rådgivergruppen haft følgende fordeling: For at belyse de landskabelige og arkitektoniske potentialer og udfordringer, har Naturstyrelsen og Realdania indledt By & Bygning Arkitekter har været rådgivende arkitekter. et samarbejde omkring syv udvalgte pilotprojekter, der COWI A/S har været rådgivende landskabsarkitekter. repræsenterer biogasanlæg i meget forskellige størrelser Projektledelsen er udført af Gottlieb Paludan Arkitekter. og i varierede landskabelige omgivelser. Projektets formål er at udvikle og formidle viden om og værktøjer til sikring af arkitektur og landskab ved planlægning, placering og projektering af biogasanlæg. Projektets overordnede -

Visionsplan for Supercykelstier 2017-2045
VISIONSPLAN SUPERCYKELSTIER 2017 - 2045 Supercykelstier 1 Version: April 2017 Sekretariatet for Supercykelstier Njalsgade 13, 2300 København S [email protected] www.supercykelstier.dk Indhold 1. Sammenfatning 4 1.1 Geografisk Afgrænsning 7 2. Fremgangsmåde 8 2.1 Dialog med interessenter 11 3. Visionsplan 12 3.1 Beskrivelse af de enkelte linjeføringer 16 1. Helsingørmotorvejen 17 2. Banesti Nivå - Vedbæk 18 3. Hillerød - Hørsholm 19 4. Langs Frederikssundsmotorvejen 20 5. Banesti Køge Bugt 21 6. Kulhusvej 22 7. Ordrup Banesti 23 8. Ring 2 nord 24 9. Borups Allé - Rantzausgade 25 10. Søgaderuten 26 11. Avedøre - Rødovre 27 12. Udretning af Ring 4-ruten i Albertslund 28 13. Banesti Hellerup-Lyngby 29 14. Vor Frue - Køge Nord 30 15. Kongens Lyngby - Klampenborg 31 Bilag Kortmateriale Hvidbog Supercykelstier 3 1. Sammenfatning Baggrund Region Hovedstaden står overfor en befolkningstilvækst de kommende 30 år, som er større end noget andet sted i landet. Region Hovedstaden er den region i Danmark med flest indbyggere på mindst plads. Det lægger pres på vejene og gør netop cyklen til et helt centralt transportmiddel, der bør være en mu- lighed til arbejde og uddannelsessteder, til glæde for både dem på cyklen og dem der får mere plads på vejene. I Region Hovedstaden er gennemsnitsafstanden til arbejdspladser 20,1 km, og ture af den læng- de, derunder og derover er nogle Supercykelstierne kan fange. 23 Kommuner i Region Hovedstaden har derfor indledt et unikt samarbejde om at skabe Supercykelstier på tværs af kommunegrænser i regionen og derved skabe højklassede cykelforbindelser mellem boligområder, arbejdspladser og kollektive trafik- knudepunkter til gavn for pendlerne. -

2. Gazeller Fordelt På
Gazeller i Københavns Amt 2006 Omsætning*/ Vækst % Navn By bruttoresultat Ansatte (1.000 kr) 940,5 1a Farma A/S** Albertslund 64343* 3 798,1 Liqtech A/S - Gazellevinder Gentofte 31783* 33 750,5 Updata Danmark A/S Glostrup 33177 19 671,7 Plaston A/S Herlev 28814* 2 670,0 Intervare A/S Rødovre 17787 47 609,7 MMJ Brolægning A/S Virum 5323 7 606,2 Cdrator A/S Ballerup 23864* 29 528,9 Scandiapack ApS Hellerup 9785 5 484,5 Spa Supply A/S Hvidovre 9317 14 481,8 Drive In Bottle Shop ApS Kastrup 12282 10 470,9 Griffin Ejendomme A/S Glostrup 237788* 9 465,6 Rovsing A/S Charlottenlund 32897 60 460,0 Segmenta A/S Brøndby 10002 16 455,6 Prof-Il Service A/S Ballerup 35454 110 446,4 H.J. Byg A/S Hedehusene 3535 7 432,0 Jens Nielsen Total- Entreprise A/S Charlottenlund 4884 13 423,3 Lyprodan A/S Hellerup 8896 - 418,5 VeriSign Denmark ApS Søborg 13776* 12 415,7 A2m Statsautoriseret Revisionsaktieselskab Brøndby 3182 5 409,4 Beton-Apoteket ApS Taastrup 5807* - 400,5 Cbrain A/S Hellerup 4324 6 375,4 Koki Europe A/S Ishøj 42402* 17 372,0 Spiritus Distillers A/S Vedbæk 26524 5 367,4 Unique Trading Danmark A/S Brøndby 8437 14 359,2 Falsing El ApS Gentofte 4009 10 357,4 Pan-Form ApS Skovlunde 6852 19 344,5 Bidsted & Co. A/S Hellerup 25427 14 339,8 Lector ApS Charlottenlund 10266 20 339,2 Copenhagen Airports International A/S Kastrup 60552* 25 338,2 Mogens Elmer A/S Kastrup 91192* 27 325,0 Kvisgårds Maskinfabrik A/S Rødovre 20413 29 306,4 HK Byg ApS Charlottenlund 12281* 9 305,6 DIBS A/S Kongens Lyngby 13097 14 300,2 Skagen Designs A/S Albertslund 21142 22 293,8 Jørgen Jacobsen Automobiler ApS Brøndby 7227 - 293,7 Investas ApS Taastrup 4142 14 289,0 Danamedic ApS Klampenborg 4400 1 287,3 Connect Partner A/S Herlev 48363 100 280,8 Sugro Danmark A/S Brøndby 64213* 5 276,5 Compare Support A/S Skovlunde 34860 77 274,1 GN Netcom A/S Ballerup 1978052* 320 271,0 Kjeld B. -

Landsdækkende Screening Af Geotermi I 28 Fjernvarmeområder
Landsdækkende screening af geotermi i 28 fjernvarmeområder Bilag 3: Områderapport for Horsens Indholdsfortegnelse – Introduktion – Data for fjernvarmeområder (COWI) – Beregning af geotermianlæg (DFG) – Beregningsresultater vedr. indpasning af geotermi (Ea) – Geologisk vurdering (GEUS) Introduktion Dette er én ud af 28 områderapporter, som viser specifikke økonomiske og produktionsmæssige resultater for hvert enkelt område. Rapporten er et bilag til hovedrapporten ”Landsdækkende screening af geotermi i 28 fjernvarmeområder”, og bør læses i sammenhæng med denne, da hovedrapporten indeholder information, der er væsentlig for at forstå resultatet. Rapporten er udarbejdet for Energistyrelsen af Dansk Fjernvarmes Geotermiselskab, COWI og Ea Energianalyse i perioden efteråret 2013 til sommeren 2015. Områderapporten indeholder den af GEUS udførte geologiske vurdering, COWIs beskrivelse af fjernvarmeområdet og den fremtidige forsyningsstruktur, Dansk Fjernvarmes Geotermiselskabs beregninger af de økonomiske og tekniske forhold i et geotermianlæg i fjernvarmeområdet, og Ea Energianalyses modelresultater fra Balmorel med varmeproduktionskapaciteter, fjernvarmeproduktion og -omkostninger over året for de fire scenarier i årene 2020, 2025 og 2035. Resultaterne skal tages med en række forbehold. Først og fremmest skal det understreges, at der er tale om en screening med det formål at give en indikation af mulighederne for geotermi. Der er ikke foretaget en fuldstændig analyse af den optimale fremtidige fjernvarmeforsyning i området. Den geologiske vurdering er alene foretaget for en enkelt lokalitet, svarende til en umiddelbart vurderet fordelagtig placering af geotermianlægget. Der kan derfor ikke drages konklusioner om hele områdets geologisk potentiale og den optimale placering for et eventuelt geotermianlæg. Modellering af områdets nuværende og forventede fremtidige fjernvarmeproduktion og -struktur er sket ud fra de data, som de var oplyst og forelå i år 2013. -
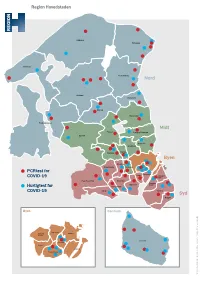
Midt Nord Syd Byen
Region Hovedstaden Gribskov Helsingør Halsnæs Gribskov Gribskov Fredensborg Helsingør Nord Helsingør Halsnæs Hillerød Halsnæs Hørsholm Fredensborg Nord Fredensborg Nord Allerød Rudersdal Hillerød Hillerød Hørsholm Hørsholm Frederikssund Allerød Midt Allerød Rudersdal Furesø Lyngby-Taarbæk Rudersdal Egedal Frederikssund Frederikssund Midt Gentofte Midt Furesø Lyngby-Taarbæk Gladsaxe Furesø Lyngby-Taarbæk Egedal Egedal Ballerup Herlev Gentofte Gentofte Gladsaxe Byen Gladsaxe Herlev Ballerup Ballerup Herlev Byen Glostrup Albertslund Rødovre Byen Glostrup Glostrup AlbertslundPCRtest Rødovrefor Albertslund Rødovre Vesterbro Valby Amager COVID-19 Vesterbro Øst Vesterbro Valby Amager Valby Amager Øst Høje-Taastrup Brøndby Øst Høje-Taastrup Brøndby Amager Høje-Taastrup Brøndby Amager Hvidovre Vest Amager Hvidovre Vest Vallensbæk Hvidovre Vest HurtigtestVallensbæk for Vallensbæk IshøjCOVID-19 Tårnby Ishøj Tårnby Ishøj Tårnby Syd Syd Syd Dragør Dragør Dragør Bornholm Byen Bornholm Byen Bornholm Byen 16. april 2021 / Opdateret Bispebjerg Bispebjerg Brønshøj- Østerbro Brønshøj- Østerbro Husum Husum 20425 RegionH Design [email protected] Design 20425 RegionH Bornholm Bornholm Nørrebro Nørrebro Vanløse Bispebjerg Brønshøj- Østerbro Vanløse Husum Indre by Indre by Frederiksberg Frederiksberg Bornholm Nørrebro Vanløse Indre by Frederiksberg PCRtest for COVID-19 Hurtigtest for COVID-19 Albertslund Ishøj Albertslund Hillerød Rådhus Hedemarksvej 14 Ishøj Østergade 20 Bibliotekstorvet 1 Trollesmindealle 27 2620 Albertslund 2635 Ishøj 2620 Albertslund 3400 -

Assessing Future Flood Hazards for Adaptation Planning in a Northern European Coastal Community
Downloaded from orbit.dtu.dk on: Nov 08, 2017 Assessing Future Flood Hazards for Adaptation Planning in a Northern European Coastal Community Sørensen, Carlo Sass; Broge, Niels H.; Molgaard, Mads R.; S. Schow, Charlotte; Thomson, Peter; Vognsen, Karsten; Knudsen, Per Published in: Frontiers in Marine Science Link to article, DOI: 10.3389/fmars.2016.00069 Publication date: 2016 Document Version Publisher's PDF, also known as Version of record Link back to DTU Orbit Citation (APA): Sørensen, C. S., Broge, N. H., Molgaard, M. R., S. Schow, C., Thomson, P., Vognsen, K., & Knudsen, P. (2016). Assessing Future Flood Hazards for Adaptation Planning in a Northern European Coastal Community. Frontiers in Marine Science, 3, [69]. DOI: 10.3389/fmars.2016.00069 General rights Copyright and moral rights for the publications made accessible in the public portal are retained by the authors and/or other copyright owners and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights. • Users may download and print one copy of any publication from the public portal for the purpose of private study or research. • You may not further distribute the material or use it for any profit-making activity or commercial gain • You may freely distribute the URL identifying the publication in the public portal If you believe that this document breaches copyright please contact us providing details, and we will remove access to the work immediately and investigate your claim. ORIGINAL RESEARCH published: 11 May 2016 doi: 10.3389/fmars.2016.00069 Assessing Future Flood Hazards for Adaptation Planning in a Northern European Coastal Community Carlo Sorensen 1, 2*, Niels H.