DOCSLIB.ORG

Spectral Density Analysis

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Spectral Density Analysis SPECTRAL DENSITY ANALYSIS: FREQUENCY DOMAIN SPECIFICATION AND MEASUREMENT OF SIGNAL STABILITY* Donald Halford, John H. Shoaf, and A. S. Risley National Bureau of Standards Boulder,Colorado 80302 USA Summary paper is complementary to NBS TN632 and relies espe- cially upon the material in it and in references 1 - 3, Stability in the frequencydomain is commonly speci- fied in terms of spectral densities. The spectral density Stability in the frequency domain is commonly concept is simple, elegant, and very useful, but care specified in terms of spectral densities. The spectral must be exercised in its use. There are several differ- density concept is simple, elegant, and very usef~l,~but ent but closely related spectral densities, which are care must be exercised in its use. There are several relevant to the specification and measurementof stability different, but closely related, spectral densities which of the frequency, phase, period, amplitude, and power of are relevant to the specification and measurement of sta- signals. Concise, tutorial descriptions of useful spectral bility of the frequency, phase, period, amplitude and densities are given in this survey. These include the power of signals. In this paper, we present a tutorial spectral densities of fluctuations of (a) phase, (b) fre- discussion of spectral densities. For background and quency, (c) fractional frequency, (d) amplitude, (e) time additional explanation of the terms, language, and 4 interval, (f) angular frequency, and (g) voltage. Also methods, we encourage reference to NBS TN632 and to included are the spectral densities of radio frequency power references 1 - 3. Other very important measures of and its two normalized components, Script X(f) and Script stability exist; we do not discuss them in this paper. %(f), the phase modulation and amplitude modulation portions, respectively. Some of the simple, often-needed relationships among these various spectral densities are Some Relevant Spectral Densities given. The use of one-sided spectral densities is rec- ommended. The relationship to two-sided spectral densi- Twelve spectral densities which are especially useful ties is explained. The concepts of cross-spectral densities. in the specification and measurement of signal stability spectral densities of time-dependent spectral densities, are listed below. Symbols otherwise undefined will be de- and smoothed spectral densities are discussed. fined in a later section, where we also will define and derive the relationships of the various quantities. In our choice of Key words(for information retrieval): Amplitude concepts and symbols, we try to optimize conformity with Fluctuations, Cross-Spectral Density, Frequency Domain, traditional usage in the field and simultaneously to mini- Frequency Noise, Modulation Noise, Noise Specification mize what we see to be the hazards of vagueness, lack and Measurement, Oscillator Noise, Phase Noise, Radio of completeness, and inconsistency. By fluctuations we Frequency Power Spectral Density, Script x(f), Script mean noise,instability, and modulation. The twelve 4)n (f), Script 32, Sidebands, Signal Stability, Spectral definitions follow, Density. S6 ~ (f)Spectral density of phasefluctu- (1) ations 6 $. The dimensionality is Introduction radians squared per hertz. The range of Fourier frequency f is The economic importance of highly stable signals, &om zero to infinity. signal sources, and signal-processors is increasing, e. g., in communications systems, navigation systems, Spectraldensity of frequencyfluc- (2) and metrology. It is accompanied by an increasing need tuations 6 V. The dimensionality is for carefully-defined and widely-disseminated terminol- hertz squared per hertz. The range ogy and language for specification and measurement of of f is from zero to infinity. We use signal stability. A significant contribution was made in the relation 2~(6V) = d( 6 +)/dt, where 1964 by the IEEE-NASA Symposium on the Definition and t is the runningtime variable. Measurement of Short-Term Frequency Stability. Its Proceedings' were followed in February 1966 by the very sy(f 1 Spectraldensity of fractionalfre- (3) useful IEEE SpecialIssue on Frequency Stability. In quency fluctuations y. The 1970 the authoritative paper, "Characterization of Fre- dimensionality is per hertz. The range quency Stability", was published b the Subcommittee of f is from zero to infinity. By definition on Frequency Stability of the IEEE. r It is the most defini- y f 6 V/V . The symbol y is defined 0 tive discussion to date of the characterization and mea- and used In reference 3, surement of frequency stability. Spectraldensity of amplitude (4) Recently Shoaf et al. have prepared a tutorial, how- fluctuations 6 E of a signal. The to-do-it technical report (NBS TN632) on specification dimensionality is amplitude (e. g., and measurement of frequency stability. The present volts) squared per hertz. The range of f is from zero to infinity. * Contribution of the National Bureau of Standards, not subject to copyright. 421 Spectraldensity of time interval (5) %(f 1 Normalized frequency domain ( 10) fluctuations 6 'c. The dimensionality measure of phase fluctuation side- is seconds squared per hertz. The bands. 6 We have defined Script a(f) range of f is from zero to infinity. to be the ratio of the power in one We use the relation 6 T= 6 $1 (2~1. phase modulation sideband, referred to the input carrier frequency, on a Spectraldensity of time interval (6) spectral density basis, to the total fluctuations. Same as S (f) . Both signal power, at Fourier frequency 6T difference f from the signal's average x and 6 T are equal to 6 @/(2svo) , frequency V , for a single specified See Eq. The is (35). symbol x signal or device. The dimensionality defined and used in reference3. is per hertz. Because here f is a frequency difference, the range of Spectral density of angular fre- f is from minus V to plus infinity. quency fluctuations 6 R. dimensionality is (radls)The /Hz. The range offis from zero to infinity. Normalized frequency domain (11) By definition, Q E 2nv. measure of fractional amplitude fluctuation sidebands of a signal. Spectraldensity of voltagefluctu- (8) We define Script m(f) to be the ratio ations 6v. The dimensionality is of the spectral density of one amplitude volts squared per hertz. The range modulation sideband to the total signal of f is from zero to infinity. Many power, at Fourier frequency difference commercial spectrum analyzers and f from the signal's average frequency V , wave analyzers exist which measure for a single specified signal or device. and display spectral density (or The dimensionality is per hertz. Because square root of spectral density) of here f is a frequency difference, the voltage fluctuations. A metrologist range of f is from minus V to plus infinity. often will choose to transduce the fluctuations of a quantity of interest Script Gf) and Script%f) are similar into analogous voltage fluctuations. functions; the former is a measure of Then the spectral density (corre- phase modulation (PM) sidebands, the sponding to fluctuations of frequency, latter is a corresponding measure of phase, time interval, amplitude, or amplitude modulation (AM) sidebands. We introduce the symbol Scriptx(f) in . ) is measured with voltage spectrum analysis equipment. order to have useful terminology for the important concept of normalized AM SF(V) Spectraldensity of (squareroot (9) sideband power. RFP of) theradio frequency power P. The S (f) Spectraldensity of fluctuations (12) power of a signal is dispersed over 6g the frequency spectrum due to noise, of any specified time-dependent instability, and modulation. The dimen- quantity g (t) . The dimensionality is the same as the dimensionalityof sionality is watts per hertz. The range 2 of the Fourier variable V is from zero the ratio g /f. The range of f is to infinity. This concept is similar from zero to infinity. The total to the concept of spectral density of variance of 6 g(t) is the integral of voltage fluctuations, S6 v(f). Typi- S (f)over all f. Thespectral 6g cally the latter, SGv(f), ismore con- density is the'distribution of the total venient for characterizing a base- variance over frequency. band signal where voltage rather than power is relevant. The former, Discussion of SpectralDensities S= (v), typically is more con- One-sided Versus Two-sided Spectral Densities venient for characterizing the dis- persion of the signal power in the Each of the above twelve spectral densities is one- vicinity of the nominal carrier sided and is on a per hertz of bandwidth density basis. frequency v . To relate the two This means that the total mean-square fluctuation (the spectral den%ties, it is necessary total variance) of frequency, for example, is given mathe- to specify the impedance associated matically by the integral of the spectral density over the with the signal. The choice of V total defined range of Fourier frequency f or f for the Fourier frequency vari- m able is somewhat arbitrary. We VarianceTotal = v(f)df, (13) prefer v for carrier-related measures and f for modulation-related measures. See later section on relationships among As another example, since Script X(f) is a normalized spectral densities. density, its integral over the defined range of difference frequency f is equal to unity, i.e., 422 this paper, we recommend their use for special 5 problems of measurement, df = 1. 0 The definite integral between two frequencies of the Time-Dependent Spectral Densities spectral density of the fluctuations of a quantity is the variance of that quantity for the frequency band The spectral density concept as used by experi- defined by the two limit frequencies. We will con- mentalists allows the spectral density to be time de- sider this in more detail later. pendent. This time dependence is an observable, and we may sometimes desire to specify the spectral Occasionally, unnecessary confusion arises density of its fluctuations, as a statistical measureof concerning one-sided versus two-sided spectral the time dependence.
Load more

Recommended publications
  • Moving Average Filters
    CHAPTER 15 Moving Average Filters The moving average is the most common filter in DSP, mainly because it is the easiest digital filter to understand and use. In spite of its simplicity, the moving average filter is optimal for a common task: reducing random noise while retaining a sharp step response. This makes it the premier filter for time domain encoded signals. However, the moving average is the worst filter for frequency domain encoded signals, with little ability to separate one band of frequencies from another. Relatives of the moving average filter include the Gaussian, Blackman, and multiple- pass moving average. These have slightly better performance in the frequency domain, at the expense of increased computation time. Implementation by Convolution As the name implies, the moving average filter operates by averaging a number of points from the input signal to produce each point in the output signal. In equation form, this is written: EQUATION 15-1 Equation of the moving average filter. In M &1 this equation, x[ ] is the input signal, y[ ] is ' 1 % y[i] j x [i j ] the output signal, and M is the number of M j'0 points used in the moving average. This equation only uses points on one side of the output sample being calculated. Where x[ ] is the input signal, y[ ] is the output signal, and M is the number of points in the average. For example, in a 5 point moving average filter, point 80 in the output signal is given by: x [80] % x [81] % x [82] % x [83] % x [84] y [80] ' 5 277 278 The Scientist and Engineer's Guide to Digital Signal Processing As an alternative, the group of points from the input signal can be chosen symmetrically around the output point: x[78] % x[79] % x[80] % x[81] % x[82] y[80] ' 5 This corresponds to changing the summation in Eq.
    [Show full text]
  • Measurement Techniques of Ultra-Wideband Transmissions
    Rec. ITU-R SM.1754-0 1 RECOMMENDATION ITU-R SM.1754-0* Measurement techniques of ultra-wideband transmissions (2006) Scope Taking into account that there are two general measurement approaches (time domain and frequency domain) this Recommendation gives the appropriate techniques to be applied when measuring UWB transmissions. Keywords Ultra-wideband( UWB), international transmissions, short-duration pulse The ITU Radiocommunication Assembly, considering a) that intentional transmissions from devices using ultra-wideband (UWB) technology may extend over a very large frequency range; b) that devices using UWB technology are being developed with transmissions that span numerous radiocommunication service allocations; c) that UWB technology may be integrated into many wireless applications such as short- range indoor and outdoor communications, radar imaging, medical imaging, asset tracking, surveillance, vehicular radar and intelligent transportation; d) that a UWB transmission may be a sequence of short-duration pulses; e) that UWB transmissions may appear as noise-like, which may add to the difficulty of their measurement; f) that the measurements of UWB transmissions are different from those of conventional radiocommunication systems; g) that proper measurements and assessments of power spectral density are key issues to be addressed for any radiation, noting a) that terms and definitions for UWB technology and devices are given in Recommendation ITU-R SM.1755; b) that there are two general measurement approaches, time domain and frequency domain, with each having a particular set of advantages and disadvantages, recommends 1 that techniques described in Annex 1 to this Recommendation should be considered when measuring UWB transmissions. * Radiocommunication Study Group 1 made editorial amendments to this Recommendation in the years 2018 and 2019 in accordance with Resolution ITU-R 1.
    [Show full text]
  • Random Signals
    Chapter 8 RANDOM SIGNALS Signals can be divided into two main categories - deterministic and random. The term random signal is used primarily to denote signals, which have a random in its nature source. As an example we can mention the thermal noise, which is created by the random movement of electrons in an electric conductor. Apart from this, the term random signal is used also for signals falling into other categories, such as periodic signals, which have one or several parameters that have appropriate random behavior. An example is a periodic sinusoidal signal with a random phase or amplitude. Signals can be treated either as deterministic or random, depending on the application. Speech, for example, can be considered as a deterministic signal, if one specific speech waveform is considered. It can also be viewed as a random process if one considers the ensemble of all possible speech waveforms in order to design a system that will optimally process speech signals, in general. The behavior of stochastic signals can be described only in the mean. The description of such signals is as a rule based on terms and concepts borrowed from probability theory. Signals are, however, a function of time and such description becomes quickly difficult to manage and impractical. Only a fraction of the signals, known as ergodic, can be handled in a relatively simple way. Among those signals that are excluded are the class of the non-stationary signals, which otherwise play an essential part in practice. Working in frequency domain is a powerful technique in signal processing. While the spectrum is directly related to the deterministic signals, the spectrum of a ran- dom signal is defined through its correlation function.
    [Show full text]
  • Lecture 7 Script
    1 Lecture 7 Script Stability of Graph Filters to Relative Perturbations Foreword 1. In this lecture, we study the stability of graph filters to relative perturbations. This is work by Alejandro Ribeiro and Fernando Gama. 2. We consider relative perturbations of shift operators such that the difference between the shift operator S and its shifted version S hat is a symmetric additive term of the form E times S plus S times E. 3. The norm of the error matrix in (1) is a measure of how close, S hat and S are. We have seen that graphs that are permutations of each other are equivalent from the perspective of running graph filters. Thus, a more convenient perturbation model is to consider a relationship in which we multiply the left hand side by a permutation matrix P sub zero. 4. We measure the size of the perturbation with the norm of this other error matrix E. We can write a relationship of the form in (2) for any permutation matrix P_0. 5. Naturally, we want to consider the permutation for which the norm of the error is minimized. The bounds we will derive here apply to any pair of shift operators that are related as per (2). They will be tightest however, for the permutation matrix P sub zero for which the nom of the error E is the smallest. Properties of the Perturbation 1. Let's study some properties of the perturbation. 2. There are two aspects of the perturbation matrix E in (2) that are important in seizing its effect on a graph filter.
    [Show full text]
  • STATISTICAL FOURIER ANALYSIS: CLARIFICATIONS and INTERPRETATIONS by DSG Pollock
    STATISTICAL FOURIER ANALYSIS: CLARIFICATIONS AND INTERPRETATIONS by D.S.G. Pollock (University of Leicester) Email: stephen [email protected] This paper expounds some of the results of Fourier theory that are es- sential to the statistical analysis of time series. It employs the algebra of circulant matrices to expose the structure of the discrete Fourier transform and to elucidate the filtering operations that may be applied to finite data sequences. An ideal filter with a gain of unity throughout the pass band and a gain of zero throughout the stop band is commonly regarded as incapable of being realised in finite samples. It is shown here that, to the contrary, such a filter can be realised both in the time domain and in the frequency domain. The algebra of circulant matrices is also helpful in revealing the nature of statistical processes that are band limited in the frequency domain. In order to apply the conventional techniques of autoregressive moving-average modelling, the data generated by such processes must be subjected to anti- aliasing filtering and sub sampling. These techniques are also described. It is argued that band-limited processes are more prevalent in statis- tical and econometric time series than is commonly recognised. 1 D.S.G. POLLOCK: Statistical Fourier Analysis 1. Introduction Statistical Fourier analysis is an important part of modern time-series analysis, yet it frequently poses an impediment that prevents a full understanding of temporal stochastic processes and of the manipulations to which their data are amenable. This paper provides a survey of the theory that is not overburdened by inessential complications, and it addresses some enduring misapprehensions.
    [Show full text]
  • Use of the Kurtosis Statistic in the Frequency Domain As an Aid In
    lEEE JOURNALlEEE OF OCEANICENGINEERING, VOL. OE-9, NO. 2, APRIL 1984 85 Use of the Kurtosis Statistic in the FrequencyDomain as an Aid in Detecting Random Signals Absmact-Power spectral density estimation is often employed as a couldbe utilized in signal processing. The objective ofthis method for signal ,detection. For signals which occur randomly, a paper is to compare the PSD technique for signal processing frequency domain kurtosis estimate supplements the power spectral witha new methodwhich computes the frequency domain density estimate and, in some cases, can be.employed to detect their presence. This has been verified from experiments vith real data of kurtosis (FDK) [2] forthe real and imaginary parts of the randomly occurring signals. In order to better understand the detec- complex frequency components. Kurtosis is defined as a ratio tion of randomlyoccurring signals, sinusoidal and narrow-band of a fourth-order central moment to the square of a second- Gaussian signals are considered, which when modeled to represent a order central moment. fading or multipath environment, are received as nowGaussian in Using theNeyman-Pearson theory in thetime domain, terms of a frequency domain kurtosis estimate. Several fading and multipath propagation probability density distributions of practical Ferguson [3] , has shown that kurtosis is a locally optimum interestare considered, including Rayleigh and log-normal. The detectionstatistic under certain conditions. The reader is model is generalized to handle transient and frequency modulated referred to Ferguson'swork for the details; however, it can signals by taking into account the probability of the signal being in a be simply said thatit is concernedwith detecting outliers specific frequency range over the total data interval.
    [Show full text]
  • 2D Fourier, Scale, and Cross-Correlation
    2D Fourier, Scale, and Cross-correlation CS 510 Lecture #12 February 26th, 2014 Where are we? • We can detect objects, but they can only differ in translation and 2D rotation • Then we introduced Fourier analysis. • Why? – Because Fourier analysis can help us with scale – Because Fourier analysis can make correlation faster Review: Discrete Fourier Transform • Problem: an image is not an analogue signal that we can integrate. • Therefore for 0 ≤ x < N and 0 ≤ u <N/2: N −1 * # 2πux & # 2πux &- F(u) = ∑ f (x),cos % ( − isin% (/ x=0 + $ N ' $ N '. And the discrete inverse transform is: € 1 N −1 ) # 2πux & # 2πux &, f (x) = ∑F(u)+cos % ( + isin% (. N x=0 * $ N ' $ N '- CS 510, Image Computaon, ©Ross 3/2/14 3 Beveridge & Bruce Draper € 2D Fourier Transform • So far, we have looked only at 1D signals • For 2D signals, the continuous generalization is: ∞ ∞ F(u,v) ≡ ∫ ∫ f (x, y)[cos(2π(ux + vy)) − isin(2π(ux + vy))] −∞ −∞ • Note that frequencies are now two- dimensional € – u= freq in x, v = freq in y • Every frequency (u,v) has a real and an imaginary component. CS 510, Image Computaon, ©Ross 3/2/14 4 Beveridge & Bruce Draper 2D sine waves • This looks like you’d expect in 2D Ø Note that the frequencies don’t have to be equal in the two dimensions. hp://images.google.com/imgres?imgurl=hFp://developer.nvidia.com/dev_content/cg/cg_examples/images/ sine_wave_perturbaon_ogl.jpg&imgrefurl=hFp://developer.nvidia.com/object/ cg_effects_explained.html&usg=__0FimoxuhWMm59cbwhch0TLwGpQM=&h=350&w=350&sz=13&hl=en&start=8&sig2=dBEtH0hp5I1BExgkXAe_kg&tbnid=fc yrIaap0P3M:&tbnh=120&tbnw=120&ei=llCYSbLNL4miMoOwoP8L&prev=/images%3Fq%3D2D%2Bsine%2Bwave%26gbv%3D2%26hl%3Den%26sa%3DG CS 510, Image Computaon, ©Ross 3/2/14 5 Beveridge & Bruce Draper 2D Discrete Fourier Transform N /2 N /2 * # 2π & # 2π &- F(u,v) = ∑ ∑ f (x, y),cos % (ux + vy)( − isin% (ux + vy)(/ x=−N /2 y=−N /2 + $ N ' $ N '.
    [Show full text]
  • 20. the Fourier Transform in Optics, II Parseval’S Theorem
    20. The Fourier Transform in optics, II Parseval’s Theorem The Shift theorem Convolutions and the Convolution Theorem Autocorrelations and the Autocorrelation Theorem The Shah Function in optics The Fourier Transform of a train of pulses The spectrum of a light wave The spectrum of a light wave is defined as: 2 SFEt {()} where F{E(t)} denotes E(), the Fourier transform of E(t). The Fourier transform of E(t) contains the same information as the original function E(t). The Fourier transform is just a different way of representing a signal (in the frequency domain rather than in the time domain). But the spectrum contains less information, because we take the magnitude of E(), therefore losing the phase information. Parseval’s Theorem Parseval’s Theorem* says that the 221 energy in a function is the same, whether f ()tdt F ( ) d 2 you integrate over time or frequency: Proof: f ()tdt2 f ()t f *()tdt 11 F( exp(j td ) F *( exp(j td ) dt 22 11 FF() *(') exp([j '])tdtd ' d 22 11 FF( ) * ( ') [2 ')] dd ' 22 112 FF() *() d F () d * also known as 22Rayleigh’s Identity. The Fourier Transform of a sum of two f(t) F() functions t g(t) G() Faft() bgt () aF ft() bFgt () t The FT of a sum is the F() + sum of the FT’s. f(t)+g(t) G() Also, constants factor out. t This property reflects the fact that the Fourier transform is a linear operation. Shift Theorem The Fourier transform of a shifted function, f ():ta Ffta ( ) exp( jaF ) ( ) Proof : This theorem is F ft a ft( a )exp( jtdt ) important in optics, because we often encounter functions Change variables : uta that are shifting (continuously) along fu( )exp( j [ u a ]) du the time axis – they are called waves! exp(ja ) fu ( )exp( judu ) exp(jaF ) ( ) QED An example of the Shift Theorem in optics Suppose that we’re measuring the spectrum of a light wave, E(t), but a small fraction of the irradiance of this light, say , takes a different path that also leads to the spectrometer.
    [Show full text]
  • Introduction to Frequency Domain Processing
    MASSACHUSETTS INSTITUTE OF TECHNOLOGY DEPARTMENT OF MECHANICAL ENGINEERING 2.14 Analysis and Design of Feedback Control Systems Introduction to Frequency Domain Processing 1 Introduction - Superposition In this set of notes we examine an alternative to the time-domain convolution operations describing the input-output operations of a linear processing system. The methods developed here use Fourier techniques to transform the temporal representation f(t) to a reciprocal frequency domain space F (jω) where the difficult operation of convolution is replaced by simple multiplication. In addition, an understanding of Fourier methods gives qualitative insights to signal processing techniques such as filtering. Linear systems,by definition,obey the principle of superposition for the forced component of their responses: If linear system is at rest at time t = 0,and is subjected to an input u(t) that is the sum of a set of causal inputs,that is u(t)=u1(t)+u2(t)+...,the response y(t) will be the sum of the individual responses to each component of the input,that is y(t)=y1(t)+y2(t)+... Suppose that a system input u(t) may be expressed as a sum of complex n exponentials n s t u(t)= aie i , i=1 where the complex coefficients ai and constants si are known. Assume that each component is applied to the system alone; if at time t = 0 the system is at rest,the solution component yi(t)is of the form sit yi(t)=(yh (t))i + aiH(si)e where (yh(t))i is a homogeneous solution.
    [Show full text]
  • Quantum Noise and Quantum Measurement
    Quantum noise and quantum measurement Aashish A. Clerk Department of Physics, McGill University, Montreal, Quebec, Canada H3A 2T8 1 Contents 1 Introduction 1 2 Quantum noise spectral densities: some essential features 2 2.1 Classical noise basics 2 2.2 Quantum noise spectral densities 3 2.3 Brief example: current noise of a quantum point contact 9 2.4 Heisenberg inequality on detector quantum noise 10 3 Quantum limit on QND qubit detection 16 3.1 Measurement rate and dephasing rate 16 3.2 Efficiency ratio 18 3.3 Example: QPC detector 20 3.4 Significance of the quantum limit on QND qubit detection 23 3.5 QND quantum limit beyond linear response 23 4 Quantum limit on linear amplification: the op-amp mode 24 4.1 Weak continuous position detection 24 4.2 A possible correlation-based loophole? 26 4.3 Power gain 27 4.4 Simplifications for a detector with ideal quantum noise and large power gain 30 4.5 Derivation of the quantum limit 30 4.6 Noise temperature 33 4.7 Quantum limit on an \op-amp" style voltage amplifier 33 5 Quantum limit on a linear-amplifier: scattering mode 38 5.1 Caves-Haus formulation of the scattering-mode quantum limit 38 5.2 Bosonic Scattering Description of a Two-Port Amplifier 41 References 50 1 Introduction The fact that quantum mechanics can place restrictions on our ability to make measurements is something we all encounter in our first quantum mechanics class. One is typically presented with the example of the Heisenberg microscope (Heisenberg, 1930), where the position of a particle is measured by scattering light off it.
    [Show full text]
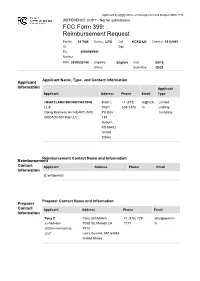
  • TV Broadcaster Relocation Fund Reimbursement Application
    Approved by OMB (Office of Management and Budget) 3060-1178 (REFERENCE COPY - Not for submission) FCC Form 399: Reimbursement Request Facility 187964 Service: LPD Call KCKS-LD Channel: 19 (UHF) ID: Sign: File 0000089941 Number: FRN: 0019530740 Eligibility Eligible Date 08/18 Status: Submitted: /2021 Applicant Name, Type, and Contact Information Applicant Information Applicant Applicant Address Phone Email Type HEARTLAND BROADCASTING Brian L +1 (913) b@tv25. Limited LLC Short 638-7373 tv Liability Doing Business As: HEARTLAND PO Box Company BROADCASTING LLC 130 Auburn, KS 66402 United States Reimbursement Contact Name and Information Reimbursement Contact Applicant Address Phone Email Information [Confidential] Preparer Contact Name and Information Preparer Contact Applicant Address Phone Email Information Tony Z Tony zumMallen +1 (816) 729- tony@qcomm. zumMallen 705B SE Melody LN 1177 tv QCommunications, #314 LLC Lee's Summit, MO 64063 United States Broadcaster Question Response Information Will the station be sharing equipment with No and another broadcast television station or Transition Plan stations (e.g., a shared antenna, co-location on a tower, use of the same transmitter room, multiple transmitters feeding a combiner, etc.)? If yes, enter the facility ID's of the other stations and click 'prefill' to download those stations' licensing information. Briefly describe transition plan Replace the transmitter, line and antenna per the channel reassignment with reasonable and customary engineering and business practices. Transmitters
    [Show full text]
  • Wavelets T( )= T( ) G F( ) F ,T ( )D F
    Notes on Wavelets- Sandra Chapman (MPAGS: Time series analysis) Wavelets Recall: we can choose ! f (t ) as basis on which we expand, ie: y(t ) = " y f (t ) = "G f ! f (t ) f f ! f may be orthogonal – chosen for "appropriate" properties. # This is equivalent to the transform: y(t ) = $ G( f )!( f ,t )d f "# We have discussed !( f ,t ) = e2!ift for the Fourier transform. Now choose different Kernel- in particular to achieve space-time localization. Main advantage- offers complete space-time localization (which may deal with issues of non- stationarity) whilst retaining scale invariant property of the ! . First, why not just use (windowed) short time DFT to achieve space-time localization? Wavelets- we can optimize i.e. have a short time interval at high frequencies, and a long time interval at low frequencies; i.e. simple Wavelet can in principle be constructed as a band- pass Fourier process. A subset of wavelets are orthogonal (energy preserving c.f Parseval theorem) and have inverse transforms. Finite time domain DFT Wavelet- note scale parameter s 1 Notes on Wavelets- Sandra Chapman (MPAGS: Time series analysis) So at its simplest, a wavelet transform is simply a collection of windowed band pass filters applied to the Fourier transform- and this is how wavelet transforms are often computed (as in Matlab). However we will want to impose some desirable properties, invertability (orthogonality) and completeness. Continuous Fourier transform: " m 1 T / 2 2!ifmt !2!ifmt x(t ) = Sme , fm = Sm = x(t )e dt # "!T / 2 m=!" T T ! i( n!m)x with orthogonality: e dx = 2!"mn "!! " x(t ) = # S( f )e2!ift df continuous Fourier transform pair: !" " S( f ) = # x(t )e!2!ift dt !" Continuous Wavelet transform: $ W !,a = x t " * t dt ( ) % ( ) ! ,a ( ) #$ 1 $ & $ ) da x(t) = ( W (!,a)"! ! ,a d! + 2 C % % a " 0 '#$ * 1 $ t # " ' Where the mother wavelet is ! " ,a (t) = ! & ) where ! is the shift parameter and a a % a ( is the scale (dilation) parameter (we can generalize to have a scaling function a(t)).
    [Show full text]