Lecture 7 Script
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
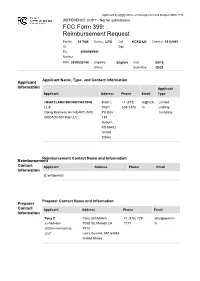
TV Broadcaster Relocation Fund Reimbursement Application
Approved by OMB (Office of Management and Budget) 3060-1178 (REFERENCE COPY - Not for submission) FCC Form 399: Reimbursement Request Facility 187964 Service: LPD Call KCKS-LD Channel: 19 (UHF) ID: Sign: File 0000089941 Number: FRN: 0019530740 Eligibility Eligible Date 08/18 Status: Submitted: /2021 Applicant Name, Type, and Contact Information Applicant Information Applicant Applicant Address Phone Email Type HEARTLAND BROADCASTING Brian L +1 (913) b@tv25. Limited LLC Short 638-7373 tv Liability Doing Business As: HEARTLAND PO Box Company BROADCASTING LLC 130 Auburn, KS 66402 United States Reimbursement Contact Name and Information Reimbursement Contact Applicant Address Phone Email Information [Confidential] Preparer Contact Name and Information Preparer Contact Applicant Address Phone Email Information Tony Z Tony zumMallen +1 (816) 729- tony@qcomm. zumMallen 705B SE Melody LN 1177 tv QCommunications, #314 LLC Lee's Summit, MO 64063 United States Broadcaster Question Response Information Will the station be sharing equipment with No and another broadcast television station or Transition Plan stations (e.g., a shared antenna, co-location on a tower, use of the same transmitter room, multiple transmitters feeding a combiner, etc.)? If yes, enter the facility ID's of the other stations and click 'prefill' to download those stations' licensing information. Briefly describe transition plan Replace the transmitter, line and antenna per the channel reassignment with reasonable and customary engineering and business practices. Transmitters -

Manga Vision: Cultural and Communicative Perspectives / Editors: Sarah Pasfield-Neofitou, Cathy Sell; Queenie Chan, Manga Artist
VISION CULTURAL AND COMMUNICATIVE PERSPECTIVES WITH MANGA ARTIST QUEENIE CHAN EDITED BY SARAH PASFIELD-NEOFITOU AND CATHY SELL MANGA VISION MANGA VISION Cultural and Communicative Perspectives EDITED BY SARAH PASFIELD-NEOFITOU AND CATHY SELL WITH MANGA ARTIST QUEENIE CHAN © Copyright 2016 Copyright of this collection in its entirety is held by Sarah Pasfield-Neofitou and Cathy Sell. Copyright of manga artwork is held by Queenie Chan, unless another artist is explicitly stated as its creator in which case it is held by that artist. Copyright of the individual chapters is held by the respective author(s). All rights reserved. Apart from any uses permitted by Australia’s Copyright Act 1968, no part of this book may be reproduced by any process without prior written permission from the copyright owners. Inquiries should be directed to the publisher. Monash University Publishing Matheson Library and Information Services Building 40 Exhibition Walk Monash University Clayton, Victoria 3800, Australia www.publishing.monash.edu Monash University Publishing brings to the world publications which advance the best traditions of humane and enlightened thought. Monash University Publishing titles pass through a rigorous process of independent peer review. www.publishing.monash.edu/books/mv-9781925377064.html Series: Cultural Studies Design: Les Thomas Cover image: Queenie Chan National Library of Australia Cataloguing-in-Publication entry: Title: Manga vision: cultural and communicative perspectives / editors: Sarah Pasfield-Neofitou, Cathy Sell; Queenie Chan, manga artist. ISBN: 9781925377064 (paperback) 9781925377071 (epdf) 9781925377361 (epub) Subjects: Comic books, strips, etc.--Social aspects--Japan. Comic books, strips, etc.--Social aspects. Comic books, strips, etc., in art. Comic books, strips, etc., in education. -

Finding Song Melody Similarities Using a Dna String Matching Algorithm
FINDING SONG MELODY SIMILARITIES USING A DNA STRING MATCHING ALGORITHM A thesis submitted to Kent State University in partial fulfillment of the requirements for the degree of Master of Science by Jeffrey Daniel Frey May, 2008 Thesis written by Jeffrey Daniel Frey B.S., Kent State University, USA, 1998 M.S., Kent State University, USA, 2008 Approved by ___________________________________ Dr. Johnnie Baker Advisor ___________________________________ Dr. Robert Walker Chair, Department of Computer Science ___________________________________ Dr. Jerry Feezel Dean, College of Arts and Sciences i i TABLE OF CONTENTS Acknowledgements......................................................................................................vii CHAPTER 1 Introduction............................................................................................1 1.1 The Problem...........................................................................................................1 1.2 Solution Concept....................................................................................................1 1.3 Approach................................................................................................................2 1.4 Document Organization..........................................................................................3 CHAPTER 2 The Need for a Solution..........................................................................4 2.1 Copyright Infringement ..........................................................................................4 -

Itis Manuscript Has Been Reproduced from the Microrilm Master
INFORMATION TO USERS "Itis manuscript has been reproduced from the microrilm master. UMI films the text directfy from the original or copy submitted. Thus, some thesis and dissertation copies are in typewriter face, while others may be from auy type of computer printer. The qnali^ of this reproduction is dqrendaat upon the gual% of the copy submitted. Broken or indistinct print, colored or poor quality illustrations and photographs; print bieedthrough, substandard margins and inproper alignment can adversely afreet reproduction. In the unlikely event that the author did not send UMI a complete m anuscr^ and there are missing pages, these will be noted. Also, if unauthorized copyright material had to be removed, a note win indicate the deletion. Oversize materials (e.g., maps, drawings, charts) are reproduced by sectioning the original, beginning at the upper left-hand comer and contmuing from left to right in equal sections with small overlaps. Eadi original is also photographed in one exposure and is included in reduced form at the back of the book. Photographs included in the original manuscript have been reproduced xerogr^hicgJJy in this copy. Higher quality 6" x 9" black and white photographic prints are available for azy photographs or illustrations appearing in this copy for an additional charge. Contact UMI directty to order. UMI A Bell & Howell Information Company 300 Nonh Zeeb Road. Ann Arbor. Ml 48106-1346 USA 313/761-4700 800.-521-0600 L inearization -B a sed G er m an S y n t a x V o l. I dissertation Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio State University By Andreas Kathol, MA ***** The Ohio State University 1995 Reading Committee: Approved by â J t . -

V=Tdnfhpazbqs
MITOCW | watch?v=TDnfhpAZBqs The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high-quality educational resources for free. To make a donation, or view additional materials from hundreds of MIT courses, visit MIT OpenCourseWare at ocw.mit.edu. PROFESSOR: OK, let's start. So last time, having dealt with the ideal gas as much as possible, we started with interacting systems. Let's say interacting gas. And the first topic that we did was what I called an approach towards interaction through the Cumulant expansion. The idea is that we certainly solved the problem where we had particles in a box and it was just a trivial system. Basically, the particles were independent of each other in the canonical ensemble. And things become interesting if you put interactions among all of the particles. Very soon, we will have a specific form of this interaction. But for the beginning, let's maintain it as general as possible. And the idea was that we are trying to calculate the partition function for a system that has a given temperature. The box has some volume V and there are N particles in it. And to do so, we have to integrate over the entirety of the phase space of N particles. So we have to integrate over all of the momenta and coordinates of e to the minus beta h. But we said that we are going to first of all, note that for identical particles, we can't tell apart the phase space if you were to make these in [? factorial ?] permutations. -

Rethinking the History of Conversion to Christianity in Japan: 1549-1644
RETHINKING THE HISTORY OF CONVERSION TO CHRISTIANITY IN JAPAN: 1549-1644 James Harry Morris A Thesis Submitted for the Degree of PhD at the University of St Andrews 2018 Full metadata for this item is available in St Andrews Research Repository at: http://research-repository.st-andrews.ac.uk/ Please use this identifier to cite or link to this item: http://hdl.handle.net/10023/15875 This item is protected by original copyright Rethinking the History of Conversion to Christianity in Japan: 1549-1644 James Harry Morris This thesis is submitted in partial fulfilment for the degree of Doctor of Philosophy (PhD) at the University of St Andrews July 2018 1 Candidate's declaration I, James Harry Morris, do hereby certify that this thesis, submitted for the degree of PhD, which is approximately 80,000 words in length, has been written by me, and that it is the record of work carried out by me, or principally by myself in collaboration with others as acknowledged, and that it has not been submitted in any previous application for any degree. I was admitted as a research student at the University of St Andrews in September 2014. I received funding from an organisation or institution and have acknowledged the funder(s) in the full text of my thesis. Date Signature of candidate Supervisor's declaration I hereby certify that the candidate has fulfilled the conditions of the Resolution and Regulations appropriate for the degree of PhD in the University of St Andrews and that the candidate is qualified to submit this thesis in application for that degree. -

Spectral Density Analysis
SPECTRAL DENSITY ANALYSIS: FREQUENCY DOMAIN SPECIFICATION AND MEASUREMENT OF SIGNAL STABILITY* Donald Halford, John H. Shoaf, and A. S. Risley National Bureau of Standards Boulder,Colorado 80302 USA Summary paper is complementary to NBS TN632 and relies espe- cially upon the material in it and in references 1 - 3, Stability in the frequencydomain is commonly speci- fied in terms of spectral densities. The spectral density Stability in the frequency domain is commonly concept is simple, elegant, and very useful, but care specified in terms of spectral densities. The spectral must be exercised in its use. There are several differ- density concept is simple, elegant, and very usef~l,~but ent but closely related spectral densities, which are care must be exercised in its use. There are several relevant to the specification and measurementof stability different, but closely related, spectral densities which of the frequency, phase, period, amplitude, and power of are relevant to the specification and measurement of sta- signals. Concise, tutorial descriptions of useful spectral bility of the frequency, phase, period, amplitude and densities are given in this survey. These include the power of signals. In this paper, we present a tutorial spectral densities of fluctuations of (a) phase, (b) fre- discussion of spectral densities. For background and quency, (c) fractional frequency, (d) amplitude, (e) time additional explanation of the terms, language, and 4 interval, (f) angular frequency, and (g) voltage. Also methods, we encourage reference to NBS TN632 and to included are the spectral densities of radio frequency power references 1 - 3. Other very important measures of and its two normalized components, Script X(f) and Script stability exist; we do not discuss them in this paper. -

{Date}. ${Publisher}. All Rights Reserved. Rights All ${Publisher}
Copyright © ${Date}. ${Publisher}. All rights reserved. © ${Date}. ${Publisher}. Copyright The Knowledge of Nature and the Nature of Knowledge in Early Modern Japan Copyright © ${Date}. ${Publisher}. All rights reserved. © ${Date}. ${Publisher}. Copyright Studies of the Weatherhead East Asian Institute, Columbia University The Studies of the Weatherhead East Asian Institute of Columbia University were inaugurated in 1962 to bring to a wider public the results of significant new research on modern and contemporary East Asia. Copyright © ${Date}. ${Publisher}. All rights reserved. © ${Date}. ${Publisher}. Copyright The Knowledge of Nature and the Nature of Knowledge in Early Modern Japan Federico Marcon Copyright © ${Date}. ${Publisher}. All rights reserved. © ${Date}. ${Publisher}. Copyright The University of Chicago Press Chicago and London Federico Marcon is assistant professor of Japanese history in the Department of History and the Department of East Asian Studies at Princeton University. The University of Chicago Press, Chicago 60637 The University of Chicago Press, Ltd., London © 2015 by the University of Chicago All rights reserved. Published 2015. Printed in the United States of America 24 23 22 21 20 19 18 17 16 15 1 2 3 4 5 ISBN- 13: 978- 0- 226- 25190- 5 (cloth) ISBN- 13: 978- 0- 226- 25206- 3 (e- book) DOI: 10.7208/chicago/9780226252063.001.0001 Library of Congress Cataloging-in-Publication Data Marcon, Federico, 1972– author. The knowledge of nature and the nature of knowledge in early modern Japan / Federico Marcon. pages cm Includes bibliographical references and index. isbn 978-0-226-25190-5 (cloth : alkaline paper) — isbn 978-0-226-25206-3 (ebook) 1. Nature study—Japan—History. -

Beets Documentation Release 1.5.1
beets Documentation Release 1.5.1 Adrian Sampson Sep 22, 2021 Contents 1 Contents 3 1.1 Guides..................................................3 1.2 Reference................................................. 14 1.3 Plugins.................................................. 45 1.4 FAQ.................................................... 120 1.5 Contributing............................................... 125 1.6 For Developers.............................................. 130 1.7 Changelog................................................ 145 Index 211 i ii beets Documentation, Release 1.5.1 Welcome to the documentation for beets, the media library management system for obsessive music geeks. If you’re new to beets, begin with the Getting Started guide. That guide walks you through installing beets, setting it up how you like it, and starting to build your music library. Then you can get a more detailed look at beets’ features in the Command-Line Interface and Configuration references. You might also be interested in exploring the plugins. If you still need help, your can drop by the #beets IRC channel on Libera.Chat, drop by the discussion board, send email to the mailing list, or file a bug in the issue tracker. Please let us know where you think this documentation can be improved. Contents 1 beets Documentation, Release 1.5.1 2 Contents CHAPTER 1 Contents 1.1 Guides This section contains a couple of walkthroughs that will help you get familiar with beets. If you’re new to beets, you’ll want to begin with the Getting Started guide. 1.1.1 Getting Started Welcome to beets! This guide will help you begin using it to make your music collection better. Installing You will need Python. Beets works on Python 3.6 or later. • macOS 11 (Big Sur) includes Python 3.8 out of the box. -
Beat Browser
Beat Browser by Jeffrey D. Goldenson B.A. Architecture Princeton University, 1999 SUBMITTED TO THE PROGRAM IN MEDIA ARTS AND SCIENCES SCHOOL OF ARCHITECTURE AND PLANNING IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF MASTER OF SCIENCE AT THE MASSACHUSETTS INSTITUTE OF TECHNOLOGY JULY 2007 ©2007 All rights reserved. T0 Nmior bb gants to T permleslee to rAprsihes and to distribute publicly papewnd electronic copies of tis thms docume be Ohel.er inpuit inany medium now, known or hereafter Wied. I A Author qe A o - Program in Media Arts and Sciences July 6, 2007 Certified by Christopher Schmandt Principal Research Scientist M.I.T. Media Laboratory Thesis Supervisor Accepted by Andrew Lippman Chairperson Department Committee on Graduate Students MA SSACHUST INSTITUTE. OF TECHNOLOGY SEP 1'A 2007 ft-OI'A., LIBRARIES 2 BEAT BROWSER by JEFFREY D. GOLDENSON Submitted to the Program in Media Arts and Sciences, School of Architecture and Planning on July 6, 2007 in partial fulfillment of the requirements for the Degree of Master of Science ABSTRACT Beat Browser is a music browsing environment that delivers immediate audio feedback while browsing arbitrarily large music collections. The goal of Beat Browser is to give users a sense of exploring "live" and continuous audio while rapidly moving between sources by mouse. It appears their entire universe of music is playing all the time, whether they're there listening or not. Beat Browser's Universal Time Base architecture keeps a central clock running that manages the playback position of every piece of music launched, orchestrating this perceptual illusion. -

Compliance Training Workshop
2/7/2018 COMPLIANCE TRAINING WORKSHOP www.floridahousing.org 1 Florida Housing Finance Corporation Mission Statement: To help our fellow Floridians obtain safe, decent, affordable housing that might otherwise be unavailable to them. 2 227 N. Bronough St., Ste. 5000 Tallahassee, Fl. 32301-1329 (850) 488-4197 Compliance Department Jan David Hines Debbie Peterson Compliance Monitoring Byrd System Administrator Specialist Manager Joketra Pat Barbie Deb Hall Thompson Goodson Wedoe Senior Analyst Senior Analyst Senior Analyst Senior Analyst B thru G M thru R S thru Z (minus V) A, H, I and V [email protected] 3 Florida Housing Finance Corporation Compliance Workshops for Multifamily Programs 1 2/7/2018 Veronica (Ronnie) Repanti National Compliance Manager 5300 West Cypress Street, Suite 261 Tampa, FL 33607 (813) 282-4800 Ext. 1513 [email protected] 4 Cynthia (Missy) Brooks Vice President 107 South Willow Avenue Tampa, FL 33606 (813) 289-9410 [email protected] 5 Craig Ellis, Director of Compliance 17633 Ashley Drive Panama City Beach, FL 32413 (850) 233-3616 ext. 272 [email protected] 6 Florida Housing Finance Corporation Compliance Workshops for Multifamily Programs 2 2/7/2018 How We Work Together Florida Housing Compliance Dept. Seltzer Management First Housing AmeriNat Group Conduct Management Review Conduct Management Review Conduct Management Review and Physical Inspection and Physical Inspection and Physical Inspection Evaluate Program Report Evaluate Program Report Evaluate Program Report Development Development Development Development Development Development 7 Florida Housing Responsibilities Monitor owner’s compliance with regulatory documents (LURA/ELIHA). Oversee compliance monitoring contracts. Report noncompliance to Board of Directors and IRS, when applicable; post noncompliance report on website. -

Avex Revivalキャンペーン 対象商品一覧
avex revivalキャンペーン 対象商品一覧 規格品番 商品名 アーティスト 発売日 フォーマット AVCD-32289 ROCK GOES ON 相川七瀬 2018/6/20 CD https://tower.jp/item/4725081 AVBD-32288 NANASE'S DAY 2017 相川七瀬 2018/2/7 DVD https://tower.jp/item/4662209 AVCD-32263 NOW OR NEVER [CD+DVD] 相川七瀬 2016/10/26 CD https://tower.jp/item/4343676 AVCD-32264 NOW OR NEVER 相川七瀬 2016/10/26 CD https://tower.jp/item/4343677 AVBD-32252 太陽と月 -NANASE'S DAY2015 & MOON DANCE- 相川七瀬 2016/3/16 DVD https://tower.jp/item/4191222 AVBD-92165 NANASE'S DAY 2014 相川七瀬 2014/12/3 DVD https://tower.jp/item/3732258 AVCD-32214 今事記 相川七瀬 2013/2/6 CD https://tower.jp/item/3192626 AVXD-32217 Live Emotion Concert Tour '97 相川七瀬 2012/12/19 Blu-ray Disc https://tower.jp/item/3172574 AVXD-32218 Live Emotion 2000 FOXTROT 相川七瀬 2012/12/19 Blu-ray Disc https://tower.jp/item/3172571 AVXD-32220 AIKAWA NANASE Live Emotion 999 相川七瀬 2012/12/19 Blu-ray Disc https://tower.jp/item/3172567 AQCD-50686 Red<期間限定生産盤> 相川七瀬 2012/3/21 CD https://tower.jp/item/3051396 AQCD-50687 ParaDOX<期間限定生産盤> 相川七瀬 2012/3/21 CD https://tower.jp/item/3051397 AVBD-32168 AIKAWA NANASE Live Emotion 999 相川七瀬 2010/11/3 DVD https://tower.jp/item/2780408 AVCD-32157 NANASE AIKAWA BEST ALBUM "ROCK or DIE" 相川七瀬 2010/2/16 CD https://tower.jp/item/2653062 AVCD-32118B Reborn [CD+DVD] 相川七瀬 2009/2/18 CD https://tower.jp/item/2489038 AVCD-32119 Reborn 相川七瀬 2009/2/18 CD https://tower.jp/item/2489039 AVCD-32057 R.U.O.K?! 相川七瀬 2005/11/9 CD https://tower.jp/item/1807278 AVBD-32036 AIKAWA NANASE Live Emotion 2004 "7 seven" 相川七瀬 2004/9/29 DVD https://tower.jp/item/1125463 AVBD-91129 BEST CLIPS