Conference Of
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Mathematics in Language
cognitive semantics 6 (2020) 243-278 brill.com/cose Mathematics in Language Richard Hudson University College London, London, England [email protected] Abstract Elementary mathematics is deeply rooted in ordinary language, which in some respects anticipates and supports the learning of mathematics, but which in other re- spects hinders this learning. This paper explores a number of areas of arithmetic and other elementary areas of mathematics, considering for each area whether it helps or hinders the young learner: counting and larger numbers, sets and brackets, algebra and variables, zero and negation, approximation, scales and relationships, and probability. The conclusion is that ordinary language anticipates the mathematics of counting, arithmetic, algebra, variables and brackets, zero and probability; but that negation, approximation and probability are particularly problematic because mathematics de- mands a different way of thinking, and different mental capacity, compared with ordi- nary language. School teachers should be aware of the mathematics already built into language so as to build on it; and they should also be able to offer special help in the conflict zones. Keywords numbers – grammar – semantics – negation – probability 1 Introduction1 This paper is about the area of language that we might call ‘mathematical language’, and has a dual function, as a contribution to cognitive semantics and as an exercise in pedagogical linguistics. Unlike earlier discussions of 1 I should like to acknowledge detailed comments on an earlier version of this paper from Neil Sheldon, as well as those of an anonymous reviewer. © Richard Hudson, 2020 | doi:10.1163/23526416-bja10005 This is an open access article distributed under the terms of the CC BY 4.0Downloaded License. -

Assessment of Options for Handling Full Unicode Character Encodings in MARC21 a Study for the Library of Congress
1 Assessment of Options for Handling Full Unicode Character Encodings in MARC21 A Study for the Library of Congress Part 1: New Scripts Jack Cain Senior Consultant Trylus Computing, Toronto 1 Purpose This assessment intends to study the issues and make recommendations on the possible expansion of the character set repertoire for bibliographic records in MARC21 format. 1.1 “Encoding Scheme” vs. “Repertoire” An encoding scheme contains codes by which characters are represented in computer memory. These codes are organized according to a certain methodology called an encoding scheme. The list of all characters so encoded is referred to as the “repertoire” of characters in the given encoding schemes. For example, ASCII is one encoding scheme, perhaps the one best known to the average non-technical person in North America. “A”, “B”, & “C” are three characters in the repertoire of this encoding scheme. These three characters are assigned encodings 41, 42 & 43 in ASCII (expressed here in hexadecimal). 1.2 MARC8 "MARC8" is the term commonly used to refer both to the encoding scheme and its repertoire as used in MARC records up to 1998. The ‘8’ refers to the fact that, unlike Unicode which is a multi-byte per character code set, the MARC8 encoding scheme is principally made up of multiple one byte tables in which each character is encoded using a single 8 bit byte. (It also includes the EACC set which actually uses fixed length 3 bytes per character.) (For details on MARC8 and its specifications see: http://www.loc.gov/marc/.) MARC8 was introduced around 1968 and was initially limited to essentially Latin script only. -

Request to Annotate North Indian Quarter Signs for Malayalam Usage Cibu Johny [email protected] Shiju Alex [email protected] Sunil V S [email protected]
Request to Annotate North Indian Quarter Signs for Malayalam Usage Cibu Johny [email protected] Shiju Alex [email protected] Sunil V S [email protected] 2017‐Sep‐22 Introduction Malayalam has following fractions involving quarter: Malayalam Unicode chart: h ttp://unicode.org/charts/PDF/U0D00.pdf However, many 19th century Malayalam documents use the North Indian quarter forms as well. Those forms are: Common Indic Number Forms Unicode chart: h ttp://www.unicode.org/charts/PDF/UA830.pdf However, this is not indicated either in the Malayalam section of the standard nor in the Common Indic Number Forms. The ‘North Indic’ common prefix for the names of the fractions could imply that it is not used in Malayalam. 1 Attestations Attestations from various sources are listed below: 1856 The Malayalam Reader Charles Collet, CMS Press Cottayam, Page 4 1868 Kerala pazhama Basel Mission Press, Mangalore, Page 59 2 1873 Sreemahabharatham Vidyavilasam, Calicut, Cover page 1856 The Malayalam Reader Charles Collet, CMS Press Cottayam, Page 14,15 3 Annotation requests Request 1 The chart for Common Indic Number Forms needs to add following to U+A830, U+A830, and U+A830: ● Used in Malayalam also Request 2 The Malayalam chart should add following annotation: 0D73 ൳ MALAYALAM FRACTION ONE QUARTER → A830 ꠰ NORTH INDIC FRACTION ONE QUARTER 0D73 ൴ MALAYALAM FRACTION ONE HALF → A831 ꠱ NORTH INDIC FRACTION ONE HALF 0D73 ൵ MALAYALAM FRACTION THREE QUARTERS → A832 ꠲ NORTH INDIC FRACTION THREE QUARTERS Request 3 In section 12.9 Malayalam: Malayalam Numbers and Punctuation, following editorial change is required: Archaic Numbers. The characters used for the archaic number system, includes those for 10, 100, and 1000, and fractions. -

Chapter 4 Mathematics As a Language
Chapter 4 Mathematics as a Language Peculiarities of Mathematical Language in the Texts of Pure Mathematics What is mathematics? Is mathematics, represented in all its modern variety, a single science? The answer to this clear-cut question was at- tempted by the French mathematicians who sign their papers with the name Nicolas Bourbaki. In their article "Architecture of Mathematics" published in Russian as an appendix to The History of Mathematics' (Bourbaki, 1948), they stated that mathematics (and certainly it is only pure mathematics that is referred to) is a uniform science. Its uniformity is given by the system of its logical constructions. A chracteristic feature of mathematics is the explicit axiomatico-deductive method of construct- ing judgments. Any mathematical paper is first of all characterized by containing a long chain of logical conclusions. But the Bourbaki say that such chaining of syllogisms is no more than a transforming mechanism. It may be applied to any system of premises. It is just an outer sign of a system, its dressing; it does not yet display the essential system of logical constructions given by the postulates. The system of postulates in mathematics is not in the least a colorful mosaic of separate initial statements. The peculiarity of mathematics lies in the ability of the system of postulates to form special concepts, mathematical structures, rich with logical consequences which may be derived from them deductively. Mathematics is principally an axioma- ' This is one of the volumes of the unique tractatus TheElernenrs of Marhernorrcs, which wos ro give the reader the fullest impression of modern mathematics, organized from the standpoint of one of the largest modern schools. -

Lecture 7 Script
1 Lecture 7 Script Stability of Graph Filters to Relative Perturbations Foreword 1. In this lecture, we study the stability of graph filters to relative perturbations. This is work by Alejandro Ribeiro and Fernando Gama. 2. We consider relative perturbations of shift operators such that the difference between the shift operator S and its shifted version S hat is a symmetric additive term of the form E times S plus S times E. 3. The norm of the error matrix in (1) is a measure of how close, S hat and S are. We have seen that graphs that are permutations of each other are equivalent from the perspective of running graph filters. Thus, a more convenient perturbation model is to consider a relationship in which we multiply the left hand side by a permutation matrix P sub zero. 4. We measure the size of the perturbation with the norm of this other error matrix E. We can write a relationship of the form in (2) for any permutation matrix P_0. 5. Naturally, we want to consider the permutation for which the norm of the error is minimized. The bounds we will derive here apply to any pair of shift operators that are related as per (2). They will be tightest however, for the permutation matrix P sub zero for which the nom of the error E is the smallest. Properties of the Perturbation 1. Let's study some properties of the perturbation. 2. There are two aspects of the perturbation matrix E in (2) that are important in seizing its effect on a graph filter. -

The Utility of Mathematics
THE UTILITY OF MATHEMATICS It is not without great surprise that we read of the efforts of modern "educators" to expunge the study of mathematics from the scholastic curriculum. It is logical, and consistent with an already incomplete, un satisfactory program, for the State to exclude religious instruc tion from the free public schools. The proscription of the study of the German language in the schools is consonant with the existing antipathy for all things German. But who has weighed mathematics in the balance of honest investigation and found it wanting? Two American soldiers training for the great conflict "over there" visited a book shop. One purchased a German grammar. His companion severely reprimanded him for his apparent weak ness, and eloquently proclaimed the uselessness of studying Ger man. "Well," said the first soldier, "you will be in an awful fix when you reach Berlin." Without a working knowledge of the German language the victorious Allies will, indeed, be at a great disadvantage when the present drive shall have led them into Germany on the road to Berlin. But what a rocky road to Ber lin! The vandalism of the retreating Hun is obstructing that road by the wanton destruction of cities, towns and villages, with their churches, bridges and every other architectural triumph of constructive engineering. The damage must be repaired when the war is· over. It will require the careful work of skilled engineers. Was there ever an engineer who attained success without the aid of mathemat ics? The war has wrought havoc and destruction wherever the tents of battle have been pitched. -

The Language of Mathematics: Towards an Equitable Mathematics Pedagogy
The Language of Mathematics: Towards an Equitable Mathematics Pedagogy Nathaniel Rounds, PhD; Katie Horneland, PhD; Nari Carter, PhD “Education, then, beyond all other devices of human origin, is the great equalizer of the conditions of men, the balance wheel of the social machinery.” (Horace Mann, 1848) 2 ©2020 Imagine Learning, Inc. Introduction From the earliest days of public education in the United States, educators have believed in education’s power as an equalizing force, an institution that would ensure equity of opportunity for the diverse population of students in American schools. Yet, for as long as we have been inspired by Mann’s vision, our history of segregation and exclusion reminds us that we have fallen short in practice. In 2019, 41% of 4th graders and 34% of 8th graders demonstrated proficiency in mathematics on the National Assessment of Educational Progress (NAEP). Yet only 20% of Black 4th graders and 28% of Hispanic 4th graders were proficient in mathematics, compared with only 14% of Black 8th grades and 20% of Hispanic 8th graders. Given these persistent inequities, how can education become “the great equalizer” that Mann envisioned? What, in short, is an equitable mathematics pedagogy? The Language of Mathematics: Towards an Equitable Mathematics Pedagogy 1 Mathematical Competencies To help think through this question, we will examine the language of mathematics and the role of language in math classrooms. This role, of course, has changed over time. Ravitch gives us this picture of math instruction in the 1890s: Some teachers used music to teach the alphabet and the multiplication tables..., with students marching up and down the isles of the classroom singing… “Five times five is twenty-five and five times six is thirty…” (Ravitch, 2001) Such strategies for the rote learning of facts and algorithms once seemed like all we needed to do to teach mathematics. -
TV Broadcaster Relocation Fund Reimbursement Application
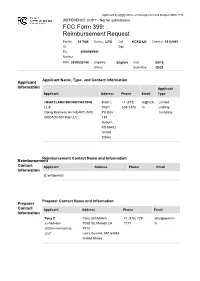
Approved by OMB (Office of Management and Budget) 3060-1178 (REFERENCE COPY - Not for submission) FCC Form 399: Reimbursement Request Facility 187964 Service: LPD Call KCKS-LD Channel: 19 (UHF) ID: Sign: File 0000089941 Number: FRN: 0019530740 Eligibility Eligible Date 08/18 Status: Submitted: /2021 Applicant Name, Type, and Contact Information Applicant Information Applicant Applicant Address Phone Email Type HEARTLAND BROADCASTING Brian L +1 (913) b@tv25. Limited LLC Short 638-7373 tv Liability Doing Business As: HEARTLAND PO Box Company BROADCASTING LLC 130 Auburn, KS 66402 United States Reimbursement Contact Name and Information Reimbursement Contact Applicant Address Phone Email Information [Confidential] Preparer Contact Name and Information Preparer Contact Applicant Address Phone Email Information Tony Z Tony zumMallen +1 (816) 729- tony@qcomm. zumMallen 705B SE Melody LN 1177 tv QCommunications, #314 LLC Lee's Summit, MO 64063 United States Broadcaster Question Response Information Will the station be sharing equipment with No and another broadcast television station or Transition Plan stations (e.g., a shared antenna, co-location on a tower, use of the same transmitter room, multiple transmitters feeding a combiner, etc.)? If yes, enter the facility ID's of the other stations and click 'prefill' to download those stations' licensing information. Briefly describe transition plan Replace the transmitter, line and antenna per the channel reassignment with reasonable and customary engineering and business practices. Transmitters -

Complete Padovan Sequences in Finite Fields Juan B. Gil
COMPLETE PADOVAN SEQUENCES IN FINITE FIELDS JUAN B. GIL Penn State Altoona, 3000 Ivyside Park, Altoona, PA 16601 MICHAEL D. WEINER Penn State Altoona, 3000 Ivyside Park, Altoona, PA 16601 CATALIN ZARA Penn State Altoona, 3000 Ivyside Park, Altoona, PA 16601 Abstract Given a prime p ≥ 5, and given 1 <κ<p − 1, we call a sequence (an)n in Fp a Φκ-sequence if it is periodic with period p − 1, and if it satisfies the linear recurrence an + an+1 = an+κ with a0 = 1. Such a sequence is said to be a complete Φκ-sequence if in addition {a0, a1,...,ap−2} = {1,...,p − 1}. For instance, every primitive root b mod p generates a complete Φκ-sequence n an = b for some (unique) κ. A natural question is whether every complete Φκ-sequence is necessarily defined by a primitive root. For κ = 2 the answer is known to be positive. In this paper we reexamine that case and investigate the case κ = 3 together with the associated cases κ = p − 2 and κ = p − 3. 1. Introduction For a prime number p ≥ 5 and a number κ ∈ {2,...,p − 2}, a sequence (an)n∈Z of elements of Fp is said to be a Φκ-sequence if a0 =1 and an+κ = an + an+1 for all n ∈ Z, (1) where “=” means (throughout this paper) equality in Fp. AΦκ-sequence is called complete if (an)n is periodic, with period p − 1, and (2) {a1,...,ap−2} = {2,...,p − 1}. (3) The case κ = 2 has been studied by Brison [1]. -

Manga Vision: Cultural and Communicative Perspectives / Editors: Sarah Pasfield-Neofitou, Cathy Sell; Queenie Chan, Manga Artist
VISION CULTURAL AND COMMUNICATIVE PERSPECTIVES WITH MANGA ARTIST QUEENIE CHAN EDITED BY SARAH PASFIELD-NEOFITOU AND CATHY SELL MANGA VISION MANGA VISION Cultural and Communicative Perspectives EDITED BY SARAH PASFIELD-NEOFITOU AND CATHY SELL WITH MANGA ARTIST QUEENIE CHAN © Copyright 2016 Copyright of this collection in its entirety is held by Sarah Pasfield-Neofitou and Cathy Sell. Copyright of manga artwork is held by Queenie Chan, unless another artist is explicitly stated as its creator in which case it is held by that artist. Copyright of the individual chapters is held by the respective author(s). All rights reserved. Apart from any uses permitted by Australia’s Copyright Act 1968, no part of this book may be reproduced by any process without prior written permission from the copyright owners. Inquiries should be directed to the publisher. Monash University Publishing Matheson Library and Information Services Building 40 Exhibition Walk Monash University Clayton, Victoria 3800, Australia www.publishing.monash.edu Monash University Publishing brings to the world publications which advance the best traditions of humane and enlightened thought. Monash University Publishing titles pass through a rigorous process of independent peer review. www.publishing.monash.edu/books/mv-9781925377064.html Series: Cultural Studies Design: Les Thomas Cover image: Queenie Chan National Library of Australia Cataloguing-in-Publication entry: Title: Manga vision: cultural and communicative perspectives / editors: Sarah Pasfield-Neofitou, Cathy Sell; Queenie Chan, manga artist. ISBN: 9781925377064 (paperback) 9781925377071 (epdf) 9781925377361 (epub) Subjects: Comic books, strips, etc.--Social aspects--Japan. Comic books, strips, etc.--Social aspects. Comic books, strips, etc., in art. Comic books, strips, etc., in education. -

Completeness Properties of Perturbed Sequences Let S Be
JOURNAL OF NUMBER THEORY 13, 44 6-455 (1981) Completeness Properties of Perturbed Sequences STEFAN A . BURR Department of Computer Science, City Univerisity of New York, City College, New York, New York 10031 AND PAUL ERDŐS Mathematical Institute, Hungarian Academy of Sciences, Budapest, Hungary Communicated by J. W. S . Cassels Received January 18, 1980 If S is an arbitrary sequence of positive integers, let P(S) be the set of all integers which are representable as a sum of distinct terms of S. Call S complete if P(S) contains all large integers, and subcomplete if P(S) contains an infinite arithmetic progression . It is shown that any sequence can be perturbed in a rather moderate way into a sequence which is not subcomplete . On the other hand, it is shown that if S is any sequence satisfying a mild growth condition, then a surprisingly gentle perturbation suffices to make S complete in a strong sense . Various related questions are also considered . 1. INTRODUCTION Let S be an arbitrary sequence of positive integers . Define P(S) to be the set of all integers which are representable as a sum of dictinct terms of S . (Having distinct terms means having distinct indices, so that the values need not be distinct .) Call a sequence S complete if P(S) contains all sufficiently large integers. Often writers have called S complete only if P(S) contains all positive integers ; we will call such a sequence entirely complete . Considerable study, spanning thirty years, has been devoted to completeness and related properties . (See [1 ; 2, Chap. -

Finding Song Melody Similarities Using a Dna String Matching Algorithm
FINDING SONG MELODY SIMILARITIES USING A DNA STRING MATCHING ALGORITHM A thesis submitted to Kent State University in partial fulfillment of the requirements for the degree of Master of Science by Jeffrey Daniel Frey May, 2008 Thesis written by Jeffrey Daniel Frey B.S., Kent State University, USA, 1998 M.S., Kent State University, USA, 2008 Approved by ___________________________________ Dr. Johnnie Baker Advisor ___________________________________ Dr. Robert Walker Chair, Department of Computer Science ___________________________________ Dr. Jerry Feezel Dean, College of Arts and Sciences i i TABLE OF CONTENTS Acknowledgements......................................................................................................vii CHAPTER 1 Introduction............................................................................................1 1.1 The Problem...........................................................................................................1 1.2 Solution Concept....................................................................................................1 1.3 Approach................................................................................................................2 1.4 Document Organization..........................................................................................3 CHAPTER 2 The Need for a Solution..........................................................................4 2.1 Copyright Infringement ..........................................................................................4