DOCSLIB.ORG

An Analysis of Moon-To -Earth Trajectories

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
An Analysis of Moon-To -Earth Trajectories AN ANALYSIS OF MOON-TO -EARTH TRAJECTORIES P. A. Penzo 30 October 1961 \ (NASA-CR-132100) AN ANALYSIS OF N73-72541 MCCN- IO-E AETH TFA JECTO R IES (Space Technoloqy Inc.) 93 p Labs., Unclas 1 00/99 03694 I / SPACE TECHFJOLOaY LABORATORIES, INC. P.O. Box 95001,Los Angeles 45,California 897 6 - 00 08 - RU - 00 0 30 October 1961 AN ANALYSIS OF MOON- TO-EARTH TRAJECTORIES P. A. Penzo Prepared for JET PROPULSION LABORATORY California Institute of Technology a Contract No. 950045 Approved E. %,T& E. H. Tompkins Associate Manager Systems Analysis Department SPACE TECHNOLOGY LABORATORIES, INC. P. 0. Box 95001 Los Angeles 45, California 8976- 0008-RU-000 Page ii CONTENTS Page I. IN TROD U C TION 1 A. The Trajectory Model 2 B. Applications of the Analytic Program 5 11. THE ANALYTIC PROGR-AM 6 A. Independent Parameters 6 B. Program Logic 10 C. Sensitivity Coefficient Routine 20 111. PROGRAM ACCURACY 22 A. Preliminary Study 22 B. Correction Scheme 26 C. Evaluation of Tau 28 D. Final Accuracy 32 IV. TRAJECTORY ANALYSIS 38 A. Earth Phase Analysis 38 B. Moon Phase Analysis 55 C. Sensitivity Coefficient Analysis 71 REFERENCES 88 8976-0008-RU-000 Page iii ACKNOWLEDGEMENTS The author wishes to thank the programmers I. Kliger, C. C. Tonies and G. Hanson for their extensive effort in developing the logic and program- ming and checking out the Analytic Lunar Return Program. He is grateful to Mrs. L. J. Martin who generated and plotted the majority of the data presented here and who carried out the investigations discussed in Section 111. Finally, he is indebted to E. H. Tompkins for checking and editing the report to its final form. 897 6 - 00 08 - RU - 000 Page iv GENERAL NOTATION (j = 1,2, 3) = coordinates of position and velocity with respect to the xj' uj earth (equatorial). yj, v (j = 1, 2, 3) = coordinates of position and velocity with respect to the j moon (equatorial). "primes" attached to position and velocity denote selenographic coordinates "bars" above position and velocity symbols denote vectors = right ascension and eclination 1, P = selenographic longitude and latitude r) = angles measured in the trajectory plane; single subscript - from perifocus e = angles measured in the equatorial plane a, e, is L! = normal conic elements (equatorial) H, J = angular momentum in earth phase; moon phase P = flight path angle measured from the vertical A = azimuth angle L = geographic longitude "bars" above quantities other than position and velocity coordinates denote those with respect to the moon = Julian Date of launch; impact Dr# Di h t = time measured from day of launch (0 GMT) h t' = time measured from day of impact (0 GMT) T = time measured from perifocus (single subscript), time measured between two points (double subscript) 89 7 6 - 00 08 - RU - 0 0 0 Page v GENERAL NOTATION (Continued) Subs c ript s : 0 = launch point b = burnout point S = point of exit from MSA i = point of impact (touchdown,) r = point of re-entry m = quantities referring to the moon 89 7 6 - 0 0 08 - RU - 0 00 Page 1 I. INTRODUCTION The present United States space program for manned lunar exploration has made it necessary to conduct thorough investigations of all trajectory and guidance aspects of lunar operations. Generally, such operations may be divided into three classes: (1) earth- to-moon trajectories in which a spacecraft is transferred from earth to the lunar s3rface or an orbit about the moon, (2) lunar rsigrn, or moo_nItp- earth trajectories where the spacecraft is launched from the surface of the moon or from a lunar orbit and returns to a designated landing site on earth, with prescribed re-entry conditions, and (3) circumlunar trajectories in which the spacecraft is launched from earth, passes within a specified distance of the moon, and returns to earth with or without an added impulse in the vicinity of the moon. This report is concerned with the second class of lunar trajectories. Its specific purpose is to provide an insight into the parametric relationships and geometric constraints existing among all of the principal trajectory variables. The procedure which was used to explore these relationships was to first develop an analytic model and an associated computer program which accu- rately describe three-dimensional moon- to-earth trajectories, and then to employ this computer program to make an extensive study of the trajectory properties. The report has been divided into four sections which are essentially independent and these may be read in an order other than as presented here, if desired. The remainder of Section I discusses the nature and application of the analytic model. Section I1 gives a complete description of the ”Analytic Lunar Return Program’’ which was used to generate information for the tra- jectory study. This material has been included since the model and computer program have other important uses besides the parametric study, and the discussion of the program logic itself displays many features of moon-to- earth trajectories. Section I11 deals with the program accuracy when compared to an n-body integration program, and describes a method by which this accuracy was greatly improved. The final section examines many of the 897 6 - 0008 - RU - 0 00 Page 2 characteristics of moon-to-earth trajectories including required lunar launch conditions, geometric constraints among variables (such as allowable launch dates and re-entry locations), launch- to-re-entry error coefficients, and midcourse correction coefficients. Much of this information is presented graphically and may be used by the reader to analyse particular lunar return flights. A. THE TRAJECTORY MODEL The analytic model upon which this study is based was first presented >;< by V. A. Egorov in 1956 [ 11. In this model, all motion in cislunar space, i. e., motion in the gravitational field of the earth-moon system, is consid- ered to be the result of two independent inverse-square force fields, that due to the earth and that due to the moon. Thus the perturbations of the sun and the planets are ignored. Further, Egorov divides earth-moon space into two regions such that only the moon's gravitational field is effective in one region and only the earth's gravitational field is effective in the remain- ing region. The dividing surface is defined as the locus of points at which the ratio between the force with which the earth perturbs the motion of a third body and the force of attraction of the moon is equal to the ratio between the perturbing force of the moon and the force of attraction of the earth. For the earth-moon system, this surface is approximately a sphere whose center is coincident with the center of the moon. The radius of this sphere is given by r = 0. C7r 2/5 5 31, 000 nautical miles S where r = distance of the moon from the earth, and m/M = ratio of the m mass of the moon to the mass of the earth. Henceforth, this sphere will be referred to as the moon's sphere of action, or the MSA. *Bracketed numbers refer to the list of references. 8 97 6 - 0008 - RU - 0 00 Page 3 Due to the eccentricity of the lunar orbit, which is about 0. 06, the distance of the moon from the earth will vary by about 10 percent during a lunar month. To be precise, the above value of rs should change by this amount; however, the effects of the original simplifying assumptions will outweigh those due to variations in rs.. Since each of the two regions defined above contains only the force field of its respective body, which is assumed to be an inverse square force field, ail motion in the model will consist of conic sections. For the particular class of trajectories delt with in this report, the motion will initiate in the vicinity of the moon, or within the MSA, and terminate near the earth. This will require that the trajectorypass through the surface bounding the MSA. During the period in which the vehicle is within the MSA the moon has rotated through an angle about the earth. This is equivalent to the earth rotating about the moon through the same angle where the MSA is assumed fixed in inertial space. Also, since the same lunar face remains pointed to the earth, except for librations, the moon will seem to revolve about its axis through the same angle within the sphere of action. For typical moon-to-earth trajectories this angle will be about 6 degrees. To an outside observer, the conic within the MSA will be non-rotating. This effect is shown in Figure 1. Once the vehicle has arrived at the surface of the MSA, it is necessary to transform its position and velocity to an earth-centered inertial coordinate system. This can be easily accomplished if the position and velocity of the moon are known at the time the vehicle passes through the surface. Specifically the earth referenced coordinates are given by, u =;tu m -- where- (y, -v) are the vehicle's position and velocity referenced to the moon and (xm, um) are the moon's position and velocity referenced to the earth. All of these variables are, of course, three dimensional vectors. As shown in Figure 1, to an outside observer there will be no discontinuity in position 8976-0008-RU-000 Page 4 SPHERE OF ACTION AT LAUNCH -1 / \ SPHERE OF ACTION AT EXIT / \ \ I \ I \ I \\\ I POINT Figure 1. Schematic of Moon-to-Earth Flight. 8976-0008-RU-000 Page 5 but there is an apparent discontinuity in the velocity since we have drawn both moon-frame inertial and earth-frame inertial phases of the trajectory in the same picture.
Load more

Recommended publications
  • Mission to Jupiter
    This book attempts to convey the creativity, Project A History of the Galileo Jupiter: To Mission The Galileo mission to Jupiter explored leadership, and vision that were necessary for the an exciting new frontier, had a major impact mission’s success. It is a book about dedicated people on planetary science, and provided invaluable and their scientific and engineering achievements. lessons for the design of spacecraft. This The Galileo mission faced many significant problems. mission amassed so many scientific firsts and Some of the most brilliant accomplishments and key discoveries that it can truly be called one of “work-arounds” of the Galileo staff occurred the most impressive feats of exploration of the precisely when these challenges arose. Throughout 20th century. In the words of John Casani, the the mission, engineers and scientists found ways to original project manager of the mission, “Galileo keep the spacecraft operational from a distance of was a way of demonstrating . just what U.S. nearly half a billion miles, enabling one of the most technology was capable of doing.” An engineer impressive voyages of scientific discovery. on the Galileo team expressed more personal * * * * * sentiments when she said, “I had never been a Michael Meltzer is an environmental part of something with such great scope . To scientist who has been writing about science know that the whole world was watching and and technology for nearly 30 years. His books hoping with us that this would work. We were and articles have investigated topics that include doing something for all mankind.” designing solar houses, preventing pollution in When Galileo lifted off from Kennedy electroplating shops, catching salmon with sonar and Space Center on 18 October 1989, it began an radar, and developing a sensor for examining Space interplanetary voyage that took it to Venus, to Michael Meltzer Michael Shuttle engines.
    [Show full text]
  • Moons Phases and Tides
    Moon’s Phases and Tides Moon Phases Half of the Moon is always lit up by the sun. As the Moon orbits the Earth, we see different parts of the lighted area. From Earth, the lit portion we see of the moon waxes (grows) and wanes (shrinks). The revolution of the Moon around the Earth makes the Moon look as if it is changing shape in the sky The Moon passes through four major shapes during a cycle that repeats itself every 29.5 days. The phases always follow one another in the same order: New moon Waxing Crescent First quarter Waxing Gibbous Full moon Waning Gibbous Third (last) Quarter Waning Crescent • IF LIT FROM THE RIGHT, IT IS WAXING OR GROWING • IF DARKENING FROM THE RIGHT, IT IS WANING (SHRINKING) Tides • The Moon's gravitational pull on the Earth cause the seas and oceans to rise and fall in an endless cycle of low and high tides. • Much of the Earth's shoreline life depends on the tides. – Crabs, starfish, mussels, barnacles, etc. – Tides caused by the Moon • The Earth's tides are caused by the gravitational pull of the Moon. • The Earth bulges slightly both toward and away from the Moon. -As the Earth rotates daily, the bulges move across the Earth. • The moon pulls strongly on the water on the side of Earth closest to the moon, causing the water to bulge. • It also pulls less strongly on Earth and on the water on the far side of Earth, which results in tides. What causes tides? • Tides are the rise and fall of ocean water.
    [Show full text]
  • The Reference Mission of the NASA Mars Exploration Study Team
    NASA Special Publication 6107 Human Exploration of Mars: The Reference Mission of the NASA Mars Exploration Study Team Stephen J. Hoffman, Editor David I. Kaplan, Editor Lyndon B. Johnson Space Center Houston, Texas July 1997 NASA Special Publication 6107 Human Exploration of Mars: The Reference Mission of the NASA Mars Exploration Study Team Stephen J. Hoffman, Editor Science Applications International Corporation Houston, Texas David I. Kaplan, Editor Lyndon B. Johnson Space Center Houston, Texas July 1997 This publication is available from the NASA Center for AeroSpace Information, 800 Elkridge Landing Road, Linthicum Heights, MD 21090-2934 (301) 621-0390. Foreword Mars has long beckoned to humankind interest in this fellow traveler of the solar from its travels high in the night sky. The system, adding impetus for exploration. ancients assumed this rust-red wanderer was Over the past several years studies the god of war and christened it with the have been conducted on various approaches name we still use today. to exploring Earth’s sister planet Mars. Much Early explorers armed with newly has been learned, and each study brings us invented telescopes discovered that this closer to realizing the goal of sending humans planet exhibited seasonal changes in color, to conduct science on the Red Planet and was subjected to dust storms that encircled explore its mysteries. The approach described the globe, and may have even had channels in this publication represents a culmination of that crisscrossed its surface. these efforts but should not be considered the final solution. It is our intent that this Recent explorers, using robotic document serve as a reference from which we surrogates to extend their reach, have can continuously compare and contrast other discovered that Mars is even more complex new innovative approaches to achieve our and fascinating—a planet peppered with long-term goal.
    [Show full text]
  • The Mathematics of the Chinese, Indian, Islamic and Gregorian Calendars
    Heavenly Mathematics: The Mathematics of the Chinese, Indian, Islamic and Gregorian Calendars Helmer Aslaksen Department of Mathematics National University of Singapore [email protected] www.math.nus.edu.sg/aslaksen/ www.chinesecalendar.net 1 Public Holidays There are 11 public holidays in Singapore. Three of them are secular. 1. New Year’s Day 2. Labour Day 3. National Day The remaining eight cultural, racial or reli- gious holidays consist of two Chinese, two Muslim, two Indian and two Christian. 2 Cultural, Racial or Religious Holidays 1. Chinese New Year and day after 2. Good Friday 3. Vesak Day 4. Deepavali 5. Christmas Day 6. Hari Raya Puasa 7. Hari Raya Haji Listed in order, except for the Muslim hol- idays, which can occur anytime during the year. Christmas Day falls on a fixed date, but all the others move. 3 A Quick Course in Astronomy The Earth revolves counterclockwise around the Sun in an elliptical orbit. The Earth ro- tates counterclockwise around an axis that is tilted 23.5 degrees. March equinox June December solstice solstice September equinox E E N S N S W W June equi Dec June equi Dec sol sol sol sol Beijing Singapore In the northern hemisphere, the day will be longest at the June solstice and shortest at the December solstice. At the two equinoxes day and night will be equally long. The equi- noxes and solstices are called the seasonal markers. 4 The Year The tropical year (or solar year) is the time from one March equinox to the next. The mean value is 365.2422 days.
    [Show full text]
  • Phases of the Moon by Patti Hutchison
    Phases of the Moon By Patti Hutchison 1 Was there a full moon last night? Some people believe that a full moon affects people's behavior. Whether that is true or not, the moon does go through phases. What causes the moon to appear differently throughout the month? 2 You know that the moon does not give off its own light. When we see the moon shining at night, we are actually seeing a reflection of the Sun's light. The part of the moon that we see shining (lunar phase) depends on the positions of the sun, moon, and the earth. 3 When the moon is between the earth and the sun, we can't see it. The sunlit side of the moon is facing away from us. The dark side is facing toward us. This phase is called the new moon. 4 As the moon moves along its orbit, the amount of reflected light we see increases. This is called waxing. At first, there is a waxing crescent. The moon looks like a fingernail in the sky. We only see a slice of it. 5 When it looks like half the moon is lighted, it is called the first quarter. Sounds confusing, doesn't it? The quarter moon doesn't refer to the shape of the moon. It is a point of time in the lunar month. There are four main phases to the lunar cycle. Four parts- four quarters. For each of these four phases, the moon has orbited one quarter of the way around the earth.
    [Show full text]
  • The Determination of Longitude in Landsurveying.” by ROBERTHENRY BURNSIDE DOWSES, Assoc
    316 DOWNES ON LONGITUDE IN LAXD SUIWETISG. [Selected (Paper No. 3027.) The Determination of Longitude in LandSurveying.” By ROBERTHENRY BURNSIDE DOWSES, Assoc. M. Inst. C.E. THISPaper is presented as a sequel tothe Author’s former communication on “Practical Astronomy as applied inLand Surveying.”’ It is not generally possible for a surveyor in the field to obtain accurate determinationsof longitude unless furnished with more powerful instruments than is usually the case, except in geodetic camps; still, by the methods here given, he may with care obtain results near the truth, the error being only instrumental. There are threesuch methods for obtaining longitudes. Method 1. By Telrgrcrph or by Chronometer.-In either case it is necessary to obtain the truemean time of the place with accuracy, by means of an observation of the sun or z star; then, if fitted with a field telegraph connected with some knownlongitude, the true mean time of that place is obtained by telegraph and carefully compared withthe observed true mean time atthe observer’s place, andthe difference between thesetimes is the difference of longitude required. With a reliable chronometer set totrue Greenwich mean time, or that of anyother known observatory, the difference between the times of the place and the time of the chronometer must be noted, when the difference of longitude is directly deduced. Thisis the simplest method where a camp is furnisl~ed with eitherof these appliances, which is comparatively rarely the case. Method 2. By Lunar Distances.-This observation is one requiring great care, accurately adjusted instruments, and some littleskill to obtain good results;and the calculations are somewhat laborious.
    [Show full text]
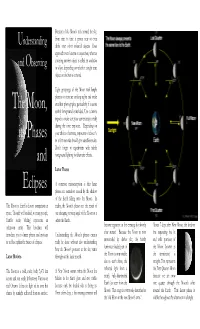
  • Understanding and Observing the Moon's Phases and Eclipses
    Because of the Moon’s trek around the sky, from time to time it passes near or even Understanding drifts over other celestial objects. Close approaches are known as conjunctions , whereas covering another object is called an occultation and Observing or eclipse, depending on whether a night time object or the Sun is covered. Tight groupings of the Moon with bright planets or stars are striking sights and make excellent photographs, particularly if a scenic The Moon, earthly foreground is included. Use a camera tripod to make sure your camera stays steady during the time exposure. Depending on your choice of camera, exposures of about ¼ its Phases to a few seconds should give useable results. Don’t forget to experiment with subtle foreground lighting for dramatic effects. and Lunar Phases Eclipses A common misconception is that lunar phases are somehow caused by the shadow of the Earth falling onto the Moon. In The Moon is Earth’s closest companion in reality, the Moon’s phases are the result of space. Though well studied, to many people, our changing viewing angle of the Moon as it Earth’s rocky ‘sibling’ represents an orbits the Earth. unknown entity. This brochure will become apparent in the evening sky shortly About 7 days after New Moon, the shadow introduce you to lunar phases and motions Understanding the Moon’s phases cannot after sunset. Because the Moon is now line separating the lit as well as explain the basics of eclipses. really be done without also understanding surrounded by darker sky, the faintly and unlit portions of how the Moon’s position in the sky varies luminous shaded part of the Moon (known as Lunar Motions throughout the lunar month.
    [Show full text]
  • The Indian Luni-Solar Calendar and the Concept of Adhik-Maas
    Volume -3, Issue-3, July 2013 The Indian Luni-Solar Calendar and the giving rise to alternative periods of light and darkness. All human and animal life has evolved accordingly, Concept of Adhik-Maas (Extra-Month) keeping awake during the day-light but sleeping through the dark nights. Even plants follow a daily rhythm. Of Introduction: course some crafty beings have turned nocturnal to take The Hindu calendar is basically a lunar calendar and is advantage of the darkness, e.g., the beasts of prey, blood– based on the cycles of the Moon. In a purely lunar sucker mosquitoes, thieves and burglars, and of course calendar - like the Islamic calendar - months move astronomers. forward by about 11 days every solar year. But the Hindu calendar, which is actually luni-solar, tries to fit together The next natural clock in terms of importance is the the cycle of lunar months and the solar year in a single revolution of the Earth around the Sun. Early humans framework, by adding adhik-maas every 2-3 years. The noticed that over a certain period of time, the seasons concept of Adhik-Maas is unique to the traditional Hindu changed, following a fixed pattern. Near the tropics - for lunar calendars. For example, in 2012 calendar, there instance, over most of India - the hot summer gives way were 13 months with an Adhik-Maas falling between to rain, which in turn is followed by a cool winter. th th August 18 and September 16 . Further away from the equator, there were four distinct seasons - spring, summer, autumn, winter.
    [Show full text]
  • Project Xpedition Is the Product of Purdue University‟S Aeronautical and Astronautical Engineering Department Senior Spacecraft Design Class in the Spring of 2009
    92 Project Xpedition Purdue University AAE 450 Spacecraft Design Spring 2009 Contents 1 – FOREWORD ........................................................................................................................................... 5 2 – INTRODUCTION ................................................................................................................................... 7 2.1 – BACKGROUND .................................................................................................................................... 7 2.2 – WHAT‟S IN THIS REPORT? .................................................................................................................. 9 2.3 – ACKNOWLEDGEMENTS .....................................................................................................................10 2.4 – ACRONYM LIST .................................................................................................................................12 3 – PROJECT OVERVIEW ....................................................................................................................... 14 3.1 – DESIGN REQUIREMENTS ...................................................................................................................14 3.2 – INTERPRETATION OF DESIGN REQUIREMENTS ...................................................................................18 3.3 – DESIGN PROCESS ..............................................................................................................................19 3.4 – RISK
    [Show full text]
  • The Moon and Eclipses
    Lecture 10 The Moon and Eclipses Jiong Qiu, MSU Physics Department Guiding Questions 1. Why does the Moon keep the same face to us? 2. Is the Moon completely covered with craters? What is the difference between highlands and maria? 3. Does the Moon’s interior have a similar structure to the interior of the Earth? 4. Why does the Moon go through phases? At a given phase, when does the Moon rise or set with respect to the Sun? 5. What is the difference between a lunar eclipse and a solar eclipse? During what phases do they occur? 6. How often do lunar eclipses happen? When one is taking place, where do you have to be to see it? 7. How often do solar eclipses happen? Why are they visible only from certain special locations on Earth? 10.1 Introduction The moon looks 14% bigger at perigee than at apogee. The Moon wobbles. 59% of its surface can be seen from the Earth. The Moon can not hold the atmosphere The Moon does NOT have an atmosphere and the Moon does NOT have liquid water. Q: what factors determine the presence of an atmosphere? The Moon probably formed from debris cast into space when a huge planetesimal struck the proto-Earth. 10.2 Exploration of the Moon Unmanned exploration: 1950, Lunas 1-3 -- 1960s, Ranger -- 1966-67, Lunar Orbiters -- 1966-68, Surveyors (first soft landing) -- 1966-76, Lunas 9-24 (soft landing) -- 1989-93, Galileo -- 1994, Clementine -- 1998, Lunar Prospector Achievement: high-resolution lunar surface images; surface composition; evidence of ice patches around the south pole.
    [Show full text]
  • Lunar Sourcebook : a User's Guide to the Moon
    3 THE LUNAR ENVIRONMENT David Vaniman, Robert Reedy, Grant Heiken, Gary Olhoeft, and Wendell Mendell 3.1. EARTH AND MOON COMPARED fluctuations, low gravity, and the virtual absence of any atmosphere. Other environmental factors are not The differences between the Earth and Moon so evident. Of these the most important is ionizing appear clearly in comparisons of their physical radiation, and much of this chapter is devoted to the characteristics (Table 3.1). The Moon is indeed an details of solar and cosmic radiation that constantly alien environment. While these differences may bombard the Moon. Of lesser importance, but appear to be of only academic interest, as a measure necessary to evaluate, are the hazards from of the Moon’s “abnormality,” it is important to keep in micrometeoroid bombardment, the nuisance of mind that some of the differences also provide unique electrostatically charged lunar dust, and alien lighting opportunities for using the lunar environment and its conditions without familiar visual clues. To introduce resources in future space exploration. these problems, it is appropriate to begin with a Despite these differences, there are strong bonds human viewpoint—the Apollo astronauts’ impressions between the Earth and Moon. Tidal resonance of environmental factors that govern the sensations of between Earth and Moon locks the Moon’s rotation working on the Moon. with one face (the “nearside”) always toward Earth, the other (the “farside”) always hidden from Earth. 3.2. THE ASTRONAUT EXPERIENCE The lunar farside is therefore totally shielded from the Earth’s electromagnetic noise and is—electro- Working within a self-contained spacesuit is a magnetically at least—probably the quietest location requirement for both survival and personal mobility in our part of the solar system.
    [Show full text]
  • Lunar Motion Motion A
    2 Lunar V. Lunar Motion Motion A. The Lunar Calendar Dr. Bill Pezzaglia B. Motion of Moon Updated 2012Oct30 C. Eclipses 3 1. Phases of Moon 4 A. The Lunar Calendar 1) Phases of the Moon 2) The Lunar Month 3) Calendars based on Moon b). Elongation Angle 5 b.2 Elongation Angle & Phase 6 Angle between moon and sun (measured eastward along ecliptic) Elongation Phase Configuration 0º New Conjunction 90º 1st Quarter Quadrature 180º Full Opposition 270º 3rd Quarter Quadrature 1 b.3 Elongation Angle & Phase 7 8 c). Aristarchus 275 BC Measures the elongation angle to be 87º when the moon is at first quarter. Using geometry he determines the sun is 19x further away than the moon. [Actually its 400x further !!] 9 Babylonians (3000 BC) note phases are 7 days apart 10 2. The Lunar Month They invent the 7 day “week” Start week on a) The “Week” “moon day” (Monday!) New Moon First Quarter b) Synodic Month (29.5 days) Time 0 Time 1 week c) Spring and Neap Tides Full Moon Third Quarter New Moon Time 2 weeks Time 3 weeks Time 4 weeks 11 b). Stone Circles 12 b). Synodic Month Stone circles often have 29 stones + 1 xtra one Full Moon to Full Moon off to side. Originally there were 30 “sarson The cycle of stone” in the outer ring of Stonehenge the Moon’s phases takes 29.53 days, or ~4 weeks Babylonians measure some months have 29 days (hollow), some have 30 (full). 2 13 c1). Tidal Forces 14 c). Tides This animation illustrates the origin of tidal forces.
    [Show full text]