Self-Affirmation Model for Football Goal Distributions
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

181201 Satzung Und Ordnungen Des SHFV
Schiedsrichterordnung Abrechnungsrichtlinien für Schiedsrichter (ab 01.01.19) Das Präsidium des SHFV hat am 01.12.2018 gemäß § 14 Abs. 3 der SHFV Schiedsrichterordnung auf Vorschlag der Spesenkommission folgende Honorar- und Kostenvergütung für Schiedsrichter, Schiedsrichterassistenten sowie Schiedsrichterbeobachter beschlossen: Vom 1. Januar 2019 bis 30. Juni 2020 gilt folgende Honorar- und Kostenvergütung: I Honorare 1. Senioren (Frauen und Männer) Euro Oberliga Schleswig-Holstein-Liga Schiedsrichter 40,00 Schiedsrichterassistent 25,00 Landesliga (Herren) Schiedsrichter 33,00 Schiedsrichterassistent 21,50 Landesliga (Frauen) Schiedsrichter 25,50 Schiedsrichterassistent 16,50 Verbandsliga Schiedsrichter 26,00 Schiedsrichterassistent 18,50 Kreisliga Herren/Frauen Schiedsrichter 20,50 Schiedsrichterassistent 14,50 Kreisebene (einschl. Alt-/Ü-Herren) Schiedsrichter 18,50 Schiedsrichterassistent 12,50 2. Juniorinnen/Junioren Euro Oberliga Schleswig-Holstein Schiedsrichter 25,50 Schiedsrichterassistent 17,50 Landesliga C- bis A-Jugend Schiedsrichter 19,00 Schiedsrichterassistent 14,50 Verbandsliga D-Jugend Schiedsrichter 15,50 Schiedsrichterassistent 11,00 Kreisebene C- bis A-Jugend Schiedsrichter 16,50 Schiedsrichterassistent 9,50 D-Jugend und jünger Schiedsrichter 12,50 Schiedsrichterassistent 7,00 185 Schiedsrichterordnung 3. Turniere in jeglicher Form (z.B. Beachsoccer/Futsal/etc.) Euro Senioren je Stunde 8,00 Jugend je Stunde 7,00 Abweichend hiervon gilt ausschließlich beim SHFV-Hallenmasters folgender Pauschalsatz: je Schiedsrichter 100,00 4. Pokal - und Freundschaftsspiele sowie Spiele in den Varianten Beachsoccer und Futsal Euro Bei Pokalspielen werden die Honorare grundsätzlich nach dem Ausrichter des Wettbewerbs errechnet. Handelt es sich um ein Spiel im Kreispokal wird nach dem oben festgesetzten Honorarsatz der Kreisliga vergütet, im Verbandspokal a) entsprechend dem Honorarsatz der Oberliga Schleswig-Holstein. Nur bei den Finalspielen im SHFV-Lottopokal gelten die folgenden Sätze: Herren und Frauen Schiedsrichter 200,00 Schiedsrichterassistent 100,00 4. -

Regional Effects of Professional Sports Franchises: Causal Evidence from Four European Football Leagues
A Service of Leibniz-Informationszentrum econstor Wirtschaft Leibniz Information Centre Make Your Publications Visible. zbw for Economics Brachert, Matthias Article — Published Version Regional effects of professional sports franchises: causal evidence from four European football leagues Regional Studies Provided in Cooperation with: Halle Institute for Economic Research (IWH) – Member of the Leibniz Association Suggested Citation: Brachert, Matthias (2020) : Regional effects of professional sports franchises: causal evidence from four European football leagues, Regional Studies, ISSN 1360-0591, Routledge, London, Iss. Latest Articles, pp. 1-12, http://dx.doi.org/10.1080/00343404.2020.1759794 This Version is available at: http://hdl.handle.net/10419/225016 Standard-Nutzungsbedingungen: Terms of use: Die Dokumente auf EconStor dürfen zu eigenen wissenschaftlichen Documents in EconStor may be saved and copied for your Zwecken und zum Privatgebrauch gespeichert und kopiert werden. personal and scholarly purposes. Sie dürfen die Dokumente nicht für öffentliche oder kommerzielle You are not to copy documents for public or commercial Zwecke vervielfältigen, öffentlich ausstellen, öffentlich zugänglich purposes, to exhibit the documents publicly, to make them machen, vertreiben oder anderweitig nutzen. publicly available on the internet, or to distribute or otherwise use the documents in public. Sofern die Verfasser die Dokumente unter Open-Content-Lizenzen (insbesondere CC-Lizenzen) zur Verfügung gestellt haben sollten, If the documents have -

NBV-Ausschreibung Spielzeit 2021-2022
Ausschreibung für die Spielzeit 2021/2022 Inhaltsverzeichnis Präambel ...................................................................................................................................................................... 2 1. Ausschreibungen ............................................................................................................................................... 2 2. Spielregeln ......................................................................................................................................................... 2 3. Teilnahmeberechtigungen ................................................................................................................................ 2 4. Meldungen ........................................................................................................................................................ 2 5. Meldetermine .................................................................................................................................................... 3 6. Meldegelder ...................................................................................................................................................... 3 7. Schiedsrichter .................................................................................................................................................... 4 8. Spieltermine ..................................................................................................................................................... -

Off Pitch: Football's Financial Integrity Weaknesses, and How to Strengthen
Off Pitch: Football’s financial integrity weaknesses, and how to strengthen them Matt Andrews and Peter Harrington CID Working Paper No. 311 January 2016 Copyright 2016 Andrews, Matt; Harrington, Peter; and the President and Fellows oF Harvard College Working Papers Center for International Development at Harvard University Off Pitch: Football’s financial integrity weaknesses, and how to strengthen them Matt Andrews and Peter Harrington1 Abstract Men’s professional football is the biggest sport in the world, producing (by our estimate) US $33 billion a year. All is not well in the sector, however, with regular scandals raising questions about the role of money in the sport. The 2015 turmoil around FIFA is obviously the most well known example, creating a crisis in confidence in the sector. This study examines these questions, and the financial integrity weaknesses they reveal; it also offers ideas to strengthen the weaknesses. The study argues that football’s financial integrity weaknesses extend far beyond FIFA. These weaknesses have emerged largely because the sector is dominated by a small elite of clubs, players and owners centered in Europe’s top leagues. The thousands of clubs beyond this elite have very little resources, constituting a vast base of ‘have-nots’ in football’s financial pyramid. This pyramid developed in recent decades, fuelled by concentrated growth in new revenue sources (like sponsorships, and broadcasting). The growth has also led to increasingly complex transactions—in player transfers, club ownership and financing (and more)—and an expansion in opportunities for illicit practices like match-fixing, money laundering and human trafficking. We argue that football’s governing bodies – including FIFA – helped establish this pyramid. -

Spielplan Oberliga Baden-Württemberg & DB Regio
Stand: 05.03.2020 Spielplan Oberliga Baden-Württemberg & DB Regio-wfv-Pokal Saison 2019/20 Datum: Begegnung: Heim/Auswärts Ergebnis/Uhrzeit: Samstag, 3. August 2019 FV Ravensburg – Kickers Auswärtsspiel (OL) 0:3 (0:0) Samstag, 10. August 2019 Kickers – Freiburger FC Heimspiel (OL) 0:0 Mittwoch, 7. August 2019 TSV Essingen – Kickers Auswärtsspiel (1. Runde wfv-Pokal) 2:6 (0:4) Samstag, 17. August 2019 FSV 08 Bissingen – Kickers Auswärtsspiel (OL) 3:2 (1:0) Freitag, 23. August 2019 Kickers – SV Sandhausen II Heimspiel (OL) 1:0 (0:0) Mittwoch, 28. August 2019 Türk Spor Neu-Ulm – Kickers Auswärtsspiel (2. Runde wfv-Pokal) 1:5 (0:5) Samstag, 31. August 2019 1.CfR Pforzheim – Kickers Auswärtsspiel (OL) 1:0 (1:0) Samstag, 7. September 2019 Kickers – 1. Göppinger SV Heimspiel (OL) 2:0 (1:0) Dienstag, 10. September 2019 Kickers – VfR Aalen Heimspiel (3. Runde wfv-Pokal) 2:1 (1:1) Samstag, 14. September 2019 Kickers – Sportfreunde Dorfmerkingen Heimspiel (OL) 5:1 (2:1) Sonntag, 22. September 2019 SGV Freiberg Fußball – Kickers Auswärtsspiel (OL) 1:3 (0:0) Samstag, 28. September 2019 Kickers – FC Nöttingen Heimspiel (OL) 1:3 (0:0) Mittwoch, 2. Oktober 2019 Kickers – TSG Balingen Heimspiel (4. Runde wfv-Pokal) 5:6 n.E. Sonntag, 6. Oktober 2019 SV Oberachern – Kickers Auswärtsspiel (OL) 4:4 (0:3) Samstag, 12. Oktober 2019 Kickers – TSV Ilshofen Heimspiel (OL) 2:2 (1:0) Samstag, 19. Oktober 2019 FC 08 Villingen – Kickers Auswärtsspiel (OL) 2:1 (2:0) Samstag, 26. Oktober 2019 Kickers – 1. FC Rielasingen-Arlen Heimspiel (OL) 1:1 (1:0) Sonntag, 3. -

German Football: History, Culture, Society
1111 2111 German Football 3 4 5111 6 7 8 9 1011 1 2 3111 German Football: History, Culture, Society provides unprecedented analysis 4 of the place of football in post-war and post-reunification Germany, revealing 5 the motives and drives underlying Germany’s successful bid to host the 2006 6 World Cup finals. 7 The contributors explore the significance of football in German sporting 8 and cultural life, showing how football has emerged as a major focus 9 for the expression of a coherent national identity and as evidence of the 20111 restoration of German national pride in the post-World War II period. 1 Major themes include: 2 3 • German football’s desire for success on the international stage 4 • Footballing expressions of local, regional and national identity 5 • The East European legacy 6 • Ethnic dynamics, migrant populations and Europeanization 7 • German football’s commercial economy 8 • Women’s football in Germany 9 • Literary and media perceptions of the German game 30111 1 With contributions from a range of disciplinary perspectives, German 2 Football illuminates key cultural moments – the 1954 victory, the founding 3 of the Bundesliga in 1963, the 1974 World Cup victory as hosts, its third 4 World Cup triumph in Italia ’90, the winning bid for 2006 – from a variety 5 of angles. 6 The result is an innovative, open-minded and critical analysis of football’s 7 burgeoning significance in German cultural life, which will be of import- 8 ance to readers in Sport Studies and German Studies alike and of interest 9 as well to followers of the world game. -

Ezana Kahsay Daniel Strachan Ben Lundt Marcel Zajac David Egbo
Ben Lundt Ezana Kahsay David Egbo Skye Harter Daniel Strachan Marcel Zajac www.adidas.com TABLE OF CONTENTS TEAM INFORMATION MEET THE 2018 AKRON ZIPS MEDIA GUIDE 2018 Table of Contents ............................................................................................. 1 Meet the Zips ....................................................................................... 20-30 Quick Facts ...................................................................................................2 Directions to Campus ....................................................................................... 3 THIS IS AKRON SOCCER Athletics Communications ............................................................................... 3 This is Akron Soccer ............................................................................. 32-35 Quick Facts ....................................................................................................... 4 MLS Draft History ................................................................................. 36-38 2018 Schedule ................................................................................................. 5 Zips In The Pros ..........................................................................................39 Series Records vs. 2018 Opponents .............................................................6-7 Zips by Class ..............................................................................................40 Roster Information .......................................................................................... -

Turning Se Ason
MICHAEL WAGG THE THE TURNING SEASON TURNING SEASON DDR-OBERLIGA REVISITED Contents Acknowledgements . 11 Vorwort . 12 A brief history of the Oberliga. 26 The magic of Mr Schmidt. 36 Jena Rules . 44 Leaning . 58 Halle: a tragedy . 68 1966, and all that . 76 Block F, Row 9 . 93 The violet revolution . 104 A spy in Sonnenberg . 116 Sparwasser shoots . .130 Hinterland: a fiction. 148 Lauzi: singular. 171 The myth of Bischofswerda . .183 The loss of Jörg Stübner . 197 Blue Monday . 219 Crossing the line . 235 Appendices . 244 Select bibliography . 254 Notes . .255 Picture credits . 256 Vorwort THERE’S A postcard on my wall that I picked up in a town called Hof. I took it from one of those stands you find near a pub doorway with a selection of cards advertising something or other. But this postcard isn’t selling anything. It’s fascinated me since I found it 17 years ago, niggling away at me like a missed sitter. I can’t remember much about Hof but I’m sure it’s a lovely town and looking at a map now I see it’s in the north-eastern corner of Bavaria where the old West meets Thuringia and Saxony in the old East. It’s just seven miles from where the Inner German border once ran its course. In the top left-hand corner of the card is part of a pennant, the type exchanged before a match for sporting friendship, with a series of bold characters printed on it like a clue to a Cold War thriller: WM74 DFV 22.6.1974 HAMBURG DDR–BRD Then three images: in black and white a close-up of a footballer just about to strike the ball with some force, two other bodies sliding over each other to stop it happening. -
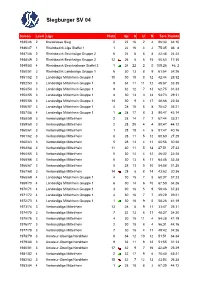
Siegburger SV 04
Siegburger SV 04 Saison Level Liga Platz Sp S U N Tore Punkte 1945/46 2 Kreisklasse Sieg 2 22 16 2 4 86:33 34:10 1946/47 1 Rheinbezirk-Liga Staffel 1 1 22 16 4 2 75:35 36: 8 1947/48 2 Rheinbezirk Bezirksliga Gruppe 2 6 24 8 8 8 42:48 24:24 1948/49 2 Rheinbezirk Bezirksliga Gruppe 2 12 26 6 5 15 50:63 17:35 1949/50 4 Rheinbezirk Bezirksklasse Staffel 3 1 24 22 2 0 109:26 46: 2 1950/51 3 Rheinbezirk Landesliga Gruppe 1 6 30 13 8 9 61:54 34:26 1951/52 3 Landesliga Mittelrhein Gruppe 1 10 30 10 8 12 42:44 28:32 1952/53 3 Landesliga Mittelrhein Gruppe 1 9 34 11 11 12 49:67 33:35 1953/54 3 Landesliga Mittelrhein Gruppe 1 9 32 12 7 13 62:75 31:33 1954/55 3 Landesliga Mittelrhein Gruppe 1 8 30 13 3 14 54:73 29:31 1955/56 3 Landesliga Mittelrhein Gruppe 1 14 30 9 4 17 48:66 22:38 1956/57 3 Landesliga Mittelrhein Gruppe 1 4 28 15 5 8 70:42 35:21 1957/58 4 Landesliga Mittelrhein Gruppe 1 1 28 17 8 3 90:47 42:14 1958/59 3 Verbandsliga Mittelrhein 2 28 14 7 7 67:44 35:21 1959/60 3 Verbandsliga Mittelrhein 2 28 20 4 4 80:47 44:12 1960/61 3 Verbandsliga Mittelrhein 1 28 18 4 6 81:47 40:16 1961/62 3 Verbandsliga Mittelrhein 8 28 11 5 12 60:60 27:29 1962/63 3 Verbandsliga Mittelrhein 5 28 13 4 11 60:56 30:26 1963/64 3 Verbandsliga Mittelrhein 11 30 11 5 14 47:51 27:33 1964/65 3 Verbandsliga Mittelrhein 5 30 14 4 12 46:32 32:28 1965/66 3 Verbandsliga Mittelrhein 5 30 13 6 11 64:46 32:28 1966/67 3 Verbandsliga Mittelrhein 5 28 13 5 10 54:58 31:25 1967/68 3 Verbandsliga Mittelrhein 14 28 6 8 14 43:62 20:36 1968/69 4 Landesliga Mittelrhein Gruppe 1 4 30 15 -

5. Jan/Feb 2002
I!I 1:,1 ~ . ~ ~ ~ ~ ~ ~ ~ MANCHESTER 2002 world's biggest relay, starts at ~ COMMONWEALTH GAMES: Buckingham Palace on Monday ~ THE QUEEN'S JUBILEE 11 March 2002 - Commonwealth ~ BATON RELAY - BIG Day. It will then travel for the I RESPONSE FOR JUBILEE next 86 days to 21 I BATON RUNNERS Commonwealth countries before ~ returning to the UK on 6th June ~ THE Queen's Baton Relay (11 when it will begin its 50 day ~ March to 25 July 2002) is the journey through Northern ~ Commonwealth Games' Ireland, Scotland, Isle of Man, I equivalent of the Olympic Torch Guernsey, Jersey and England I Relay. For the Baton Relay in (starting in Gloucester on 17 ~ Jubilee Year, the search was on June and finally being carried ~ for 2,500 Jubilee Runners to into the City of Manchester ~ carry the Baton around the UK, Stadium for Opening Ceremony ~ and although over subscribed in of the XVII Games on 25 July). i the North West, there were still The Baton has a flashing light ~ plenty of opportunities to that pulsates in time to the I participate in the rest of England runner's heart beat. It is linked ~ (from 17 June to 25 July). Karen up to a satellite orbiting the ~ Tonge ([email protected] Earth that will allow the world to ~ Tel. 01928 563640), the follow - in real time - the relay's I organiser of the Commonwealth journey on the Commonwealth ~ Games Table Tennis Games website. Anlessage is ~ Competition, was particularly contained in the top of The ~ keen that suitable table tennis Baton. ~ people were involved. -

„Sport Und Sicherheit“ Bericht Zur Evaluation Der Rahmenkonzeption
Niedersächsischer Ausschuss „Sport und Sicherheit“ Bericht zur Evaluation der Rahmenkonzeption „Sicherheit bei Fußballspielen niedersächsischer Vereine im Amateurbereich“ Stand: 21.09.2010 1 Allgemeines Vor dem Hintergrund vermehrter Anzeichen für ein zunehmend gewalttätiges Fanverhalten im Zusammenhang mit Fußballspielen im Amateurbereich haben das Niedersächsische Ministerium für Inneres und Sport und der Niedersächsische Fußballverband (NFV) im Dezember 2006 eine ständige Niedersächsische Kommission sowie unterhalb dieser einen Ausschuss Sport und Si- cherheit ins Leben gerufen. Ein dort im Juni 2007 erstelltes Lagebild für die Bereiche der damaligen Fußball-Oberliga Nord sowie der Niedersachsenliga hat aufgezeigt, dass in diesen Ligen ein ausgeprägtes Gewaltprob- lem zwar nicht vorliegt, dennoch aber ein Problemfanpotenzial existiert bzw. mobilisierbar ist, dessen Drang zur Gewaltanwendung konsequent entgegen zu treten ist. Die diesbezüglichen Maßnahmen der Polizei und des NFV sowie der von ihm vertretenen Verei- ne sind im Anschluss mit der gemeinsam erarbeiteten Rahmenkonzeption „Sicherheit bei Fuß- ballspielen niedersächsischer Vereine im Amateurbereich“ vom 4.12.2007 zielgerichtet gebündelt worden. Die mit Beginn der Saison 2008/2009 in Kraft getretene Konzeption soll Erscheinungsformen gruppendynamischer Gewalt in den niedersächsischen Fußball-Amateurligen vorbeugen bzw. bekämpfen und dazu beitragen, die personellen Aufwände der Polizei und der beteiligten Vereine auf einen angemessenen Rahmen zu begrenzen und zu verteilen. Dazu -

HVM-DF 2021-2022.Pdf (440,8 Kib)
Inhaltsverzeichnis I Vorbemerkung II Durchführungsbestimmungen für die Meisterschaftsspiele der Verbands- klassen des HV Mittelrhein e.V. in der Spielsaison 2021/2022 1 Allgemeine Bestimmungen 2 Spieltechnische Bestimmungen 3 Spielmodalitäten, Auf- und Abstieg 4 Wirtschaftliche Bestimmungen 5 Zusatzbestimmungen der weiblichen und männlichen Jugend III HVM Pokalspiele IV Anschriften Spielleitende Stellen und des Schiedsrichterwartes Versand der Spielberichte V Gebühren- und Bußgeldkatalog I. Vorbemerkung Alle Vereine werden im Interesse einer guten und sportlichen Abwicklung der Spiele gebeten, die Durchführungsbestimmungen und Hinweise dazu genau zu beachten. Den Vereinen wünschen wir für die Spielsaison 2021/2022 einen guten Verlauf und sportlichen Erfolg. Köln, im August 2021 2 Handballverband Mittelrhein e.V. Lutz Rohmer Karl-Walter Marx Elke Meesters Boris Lietz Präsident Vizepräsident Vizepräsident Vizepräsident Spielbetrieb Finanzen Jugend Anmerkung: Um eine sprachliche Vereinfachung zu erreichen, wird in diesen Durchführungsbestimmungen generell für weibliche und männliche Spieler, Offizielle, Schiedsrichter und andere Personen jeweils die männliche Form benutzt. Zusätzliche Informationen: Der HVM ist mit seinen Verbandsstaffeln im Internet vertreten und benutzt dafür das Programm nuLiga-Handball. Unter der Internet-Adresse https://hvmittelrhein-handball.liga.nu/ finden Sie die aktuellen Spielergebnisse, Spieltermine, SR-Ansetzungen, etc. Die Durchführungsbestimmungen zur laufenden Spielsaison sowie die Amtlichen Mitteilungen werden