Circumbinary Disk Evolution Using Only a Small Number of Particles All Having the Same Binary
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Durham E-Theses
Durham E-Theses First visibility of the lunar crescent and other problems in historical astronomy. Fatoohi, Louay J. How to cite: Fatoohi, Louay J. (1998) First visibility of the lunar crescent and other problems in historical astronomy., Durham theses, Durham University. Available at Durham E-Theses Online: http://etheses.dur.ac.uk/996/ Use policy The full-text may be used and/or reproduced, and given to third parties in any format or medium, without prior permission or charge, for personal research or study, educational, or not-for-prot purposes provided that: • a full bibliographic reference is made to the original source • a link is made to the metadata record in Durham E-Theses • the full-text is not changed in any way The full-text must not be sold in any format or medium without the formal permission of the copyright holders. Please consult the full Durham E-Theses policy for further details. Academic Support Oce, Durham University, University Oce, Old Elvet, Durham DH1 3HP e-mail: [email protected] Tel: +44 0191 334 6107 http://etheses.dur.ac.uk me91 In the name of Allah, the Gracious, the Merciful >° 9 43'' 0' eji e' e e> igo4 U61 J CO J: lic 6..ý v Lo ý , ý.,, "ý J ýs ýºý. ur ý,r11 Lýi is' ý9r ZU LZJE rju No disaster can befall on the earth or in your souls but it is in a book before We bring it into being; that is easy for Allah. In order that you may not grieve for what has escaped you, nor be exultant at what He has given you; and Allah does not love any prideful boaster. -

Fy10 Budget by Program
AURA/NOAO FISCAL YEAR ANNUAL REPORT FY 2010 Revised Submitted to the National Science Foundation March 16, 2011 This image, aimed toward the southern celestial pole atop the CTIO Blanco 4-m telescope, shows the Large and Small Magellanic Clouds, the Milky Way (Carinae Region) and the Coal Sack (dark area, close to the Southern Crux). The 33 “written” on the Schmidt Telescope dome using a green laser pointer during the two-minute exposure commemorates the rescue effort of 33 miners trapped for 69 days almost 700 m underground in the San Jose mine in northern Chile. The image was taken while the rescue was in progress on 13 October 2010, at 3:30 am Chilean Daylight Saving time. Image Credit: Arturo Gomez/CTIO/NOAO/AURA/NSF National Optical Astronomy Observatory Fiscal Year Annual Report for FY 2010 Revised (October 1, 2009 – September 30, 2010) Submitted to the National Science Foundation Pursuant to Cooperative Support Agreement No. AST-0950945 March 16, 2011 Table of Contents MISSION SYNOPSIS ............................................................................................................ IV 1 EXECUTIVE SUMMARY ................................................................................................ 1 2 NOAO ACCOMPLISHMENTS ....................................................................................... 2 2.1 Achievements ..................................................................................................... 2 2.2 Status of Vision and Goals ................................................................................ -

INAUGURAL – DISSERTATION Dipl.-Phys. Alexander A. Schegerer
INAUGURAL – DISSERTATION zur Erlangung der Doktorwurde¨ der Naturwissenschaftlich-Mathematischen Gesamtfakult¨at der Ruprecht - Karls - Universit¨at Heidelberg vorgelegt von Dipl.-Phys. Alexander A. Schegerer, geboren in Kaufbeuren Tag der mundlichen¨ Prufung:¨ 17. Oktober 2007 II Struktur- und Staubentwicklung in zirkumstellaren Scheiben um T Tauri-Sterne Analyse und Modellierung hochaufl¨osender Beobachtungen in verschiedenen Wellenl¨angenbereichen Gutachter: Prof. Dr. Thomas Henning Prof. Dr. Wolfgang Duschl IV Meinen Eltern, Maria-Christa und Wolfgang Schegerer, gewidmet. VI Thema Im Zentrum dieser Doktorarbeit steht die Untersuchung der inneren Strukturen zirkumstella- rer Scheiben um T Tauri-Sterne sowie die Analyse zirkumstellarer Staub- und Eisteilchen und ihres Einflusses auf die Scheibenstruktur. Unter Zuhilfenahme von theoretisch berechneten Vergleichsspektren gibt der Verlauf der 10 µm-Emissionsbande in den Spektren junger stellarer Objekte Hinweise auf den Entwick- lungsgrad von Silikatstaub. Die Silikatbanden von 27 T Tauri-Objekten werden analysiert, um nach potentiell vorliegenden Korrelationen zwischen der Silikatstaubzusammensetzung und den stellaren Eigenschaften zu suchen. Analog erlaubt das Absorptionsband bei 3 µm, das dem Wassereis zugeschrieben wird, eine Untersuchung der Entwicklung von Eisk¨ornern in jungen stellaren Objekten. Erstmals ist es gelungen, kristallines Wassereis im Spektrum eines T Tauri-Objektes nachzuweisen. Unser wichtigstes Hilfsmittel zur Analyse der Temperatur- und Dichtestrukturen zirkum- stellarer -

Instrumental Methods for Professional and Amateur
Instrumental Methods for Professional and Amateur Collaborations in Planetary Astronomy Olivier Mousis, Ricardo Hueso, Jean-Philippe Beaulieu, Sylvain Bouley, Benoît Carry, Francois Colas, Alain Klotz, Christophe Pellier, Jean-Marc Petit, Philippe Rousselot, et al. To cite this version: Olivier Mousis, Ricardo Hueso, Jean-Philippe Beaulieu, Sylvain Bouley, Benoît Carry, et al.. Instru- mental Methods for Professional and Amateur Collaborations in Planetary Astronomy. Experimental Astronomy, Springer Link, 2014, 38 (1-2), pp.91-191. 10.1007/s10686-014-9379-0. hal-00833466 HAL Id: hal-00833466 https://hal.archives-ouvertes.fr/hal-00833466 Submitted on 3 Jun 2020 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Instrumental Methods for Professional and Amateur Collaborations in Planetary Astronomy O. Mousis, R. Hueso, J.-P. Beaulieu, S. Bouley, B. Carry, F. Colas, A. Klotz, C. Pellier, J.-M. Petit, P. Rousselot, M. Ali-Dib, W. Beisker, M. Birlan, C. Buil, A. Delsanti, E. Frappa, H. B. Hammel, A.-C. Levasseur-Regourd, G. S. Orton, A. Sanchez-Lavega,´ A. Santerne, P. Tanga, J. Vaubaillon, B. Zanda, D. Baratoux, T. Bohm,¨ V. Boudon, A. Bouquet, L. Buzzi, J.-L. Dauvergne, A. -

Pulsating Components in Binary and Multiple Stellar Systems---A
Research in Astron. & Astrophys. Vol.15 (2015) No.?, 000–000 (Last modified: — December 6, 2014; 10:26 ) Research in Astronomy and Astrophysics Pulsating Components in Binary and Multiple Stellar Systems — A Catalog of Oscillating Binaries ∗ A.-Y. Zhou National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100012, China; [email protected] Abstract We present an up-to-date catalog of pulsating binaries, i.e. the binary and multiple stellar systems containing pulsating components, along with a statistics on them. Compared to the earlier compilation by Soydugan et al.(2006a) of 25 δ Scuti-type ‘oscillating Algol-type eclipsing binaries’ (oEA), the recent col- lection of 74 oEA by Liakos et al.(2012), and the collection of Cepheids in binaries by Szabados (2003a), the numbers and types of pulsating variables in binaries are now extended. The total numbers of pulsating binary/multiple stellar systems have increased to be 515 as of 2014 October 26, among which 262+ are oscillating eclipsing binaries and the oEA containing δ Scuti componentsare updated to be 96. The catalog is intended to be a collection of various pulsating binary stars across the Hertzsprung-Russell diagram. We reviewed the open questions, advances and prospects connecting pulsation/oscillation and binarity. The observational implication of binary systems with pulsating components, to stellar evolution theories is also addressed. In addition, we have searched the Simbad database for candidate pulsating binaries. As a result, 322 candidates were extracted. Furthermore, a brief statistics on Algol-type eclipsing binaries (EA) based on the existing catalogs is given. We got 5315 EA, of which there are 904 EA with spectral types A and F. -
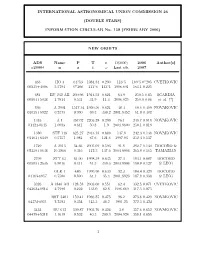
CIRCULAR No. 158 (FEBRUARY 2006)
INTERNATIONAL ASTRONOMICAL UNION COMMISSION 26 (DOUBLE STARS) INFORMATION CIRCULAR No. 158 (FEBRUARY 2006) NEW ORBITS ADS Name P T e Ω(2000) 2006 Author(s) α2000δ n a i ω Last ob. 2007 463 HO 3 64y53 1984.84 0.290 116◦5 169◦5 0′′205 CVETKOVIC 00335+4006 5.5784 0′′388 111◦6 143◦1 1996.691 163.1 0.225 684 BU 232 AB 200.96 1914.52 0.621 64.9 250.5 0.85 SCARDIA 00504+5038 1.7914 0.531 31.9 11.4 2006.025 250.9 0.86 et al. (*) 836 A 2901 1517.34 1950.56 0.621 48.4 60.6 0.409 NOVAKOVIC 01015+6922 0.2373 0.990 69.3 330.2 2001.8352 61.0 0.408 1345 A 1 357.02 2205.28 0.299 76.1 249.7 0.818 NOVAKOVIC 01424-0645 1.0083 0.641 50.8 1.9 2003.9600 250.1 0.819 1380 STF 148 625.27 2013.18 0.689 147.9 242.3 0.136 NOVAKOVIC 01461+6349 0.5757 1.081 67.6 121.6 1997.03 252.3 0.137 1729 A 2013 34.66 2005.69 0.593 91.8 282.7 0.130 DOCOBO & 02159+0638 10.3866 0.346 112.3 137.6 2004.9904 265.8 0.165 TAMAZIAN 2799 STT 65 61.00 1998.39 0.635 27.3 183.1 0.087 DOCOBO 03503+2535 5.9016 0.411 84.3 340.5 2004.9906 190.0 0.127 & LING GLE 1 480. -

The University of Wisconsin-Madison Department of Astronomy Madison, WI 53706
The University of Wisconsin-Madison Department of Astronomy Madison, WI 53706 This description covers the Department’s activ- was at Lick Observatory (Santa Cruz) and is inter- ities from October 1, 2003, through September 30, ested in instrumentation and the nature of QSOs. 2004. It only refers to papers that were published Prof. Christopher Anderson retired at the end of the within this period. It ignores research that is under spring semester and was appointed Emeritus Pro- way and papers that are in press or submitted. fessor. Linda Sparke completed three years’ duty Gallagher will assume full editorship of the As- as Chair and was replaced in that capacity by John tronomical Journal on 1 January 2005, following Hoessel. Barger and Lazarian were promoted to his selection in May. Associate Professor. The faculty consist of Pro- The Southern African Large Telescope (SALT) fessors Cassinelli, Churchwell, Gallagher, Hoes- will undergo engineering tests in 2005. Its Prime sel (Chair), Mathieu, Nordsieck, Reynolds, Savage, Focus Imaging Spectrograph (Nordsieck, PI; Burgh, Sparke, Zweibel, and Associate Professors Barger, scientist) will be shipped to South Africa in early Bershady, Lazarian, and Wilcots. Bless and Mathis 2005. The Spitzer Space Telescope Legacy Sci- are Professors Emeriti residing in Madison. Robert ence project GLIMPSE, a near-infrared imaging Benjamin is an Assistant Professor of Physics at survey of the inner Galactic plane (Churchwell, PI), UW-Whitewater and served in Madison as Pro- is producing excellent scientific results. Other ma- gram Director of the Summer Research Opportu- jor thrusts include studies of star formation, extra- nities Program. Percival is a Scientist; Wakker, an galactic structure and evolution, properties of inter- Associate Scientist. -

Annual Performance Report 2011-2012 Research Uncovering Tomorrow
Annual Performance Report 2011-2012 Research uncovering tomorrow NRF APR Cover 13 Aug Final 4.indd 1 2012/08/13 3:03 PM Research uncovering tomorrow What is the origin of matter? What is the universe made of? What happened a fraction of a second after the Big Bang and how does that impact on the future? How does research today uncover tomorrow? During 2008 the NRF adopted its longer-term strategy, Vision 2015. The NRF Annual Performance Report 2011-2012 reviews the progress the entity has made since embracing the five strategic goals of Vision 2015. In order to create a better future, we need to learn from the past and watch the present. This report therefore reflects on what has been achieved with a view to make every step count on the challenging road ahead. NRF Annual Performance Report 2011-2012 ISBN: 978-1-86868-076-4 PO Box 2600 Pretoria 0001 Tel: +27 12 481 4000 Fax: +27 12 349 1179 E-mail: [email protected] NRF APR Cover 13 Aug Final 4.indd 2 2012/08/13 3:03 PM Introduction The National Research Foundation (NRF) is proud to present its Annual Performance Report for 2011/12. This report offers an overview of the activities and performance of the NRF and highlights the impact of a small selection of NRF-supported research projects. XiTsonga Sepedi National Research Foundation (NRF) ya tinyungubyisa ku andlala National Research Foundation (NRF) ka boikgantšho e hlagiša Pego Xiviko xa yona xa Lembe ra 2011/12. Xiviko lexi xi nyika mbalango ya yona ya Ngwaga wa 2011/12. -

Azərbaycan Astronomiya Jurnali
Azərbaycan Milli Elmlər Akademiyası AZƏRBAYCAN ASTRONOMİYA JURNALI Cild 7 – № 4 – 2012 Azerbaijan National Academy of Sciences Национальная Академия Наук Азербайджана AZERBAIJANI АСТРОНОМИЧЕСКИЙ ASTRONOMICAL ЖУРНАЛ JOURNAL АЗЕРБАЙДЖАНА Volume 7 – No 4 – 2012 Том 7 – № 4 – 2012 Azərbaycan Milli Elmlər Akademiyasının “AZƏRBAYCAN ASTRONOMIYA JURNALI” Azərbaycan Milli Elmlər Akademiyası (AMEA) Rəyasət Heyətinin 28 aprel 2006-cı il tarixli 50-saylı Sərəncamı ilə təsis edilmişdir. Baş Redaktor: Ə.S. Quliyev Baş Redaktorun Müavini: E.S. Babayev Məsul Katib: P.N. Şustarev REDAKSIYA HEYƏTİ: Cəlilov N.S. AMEA N.Tusi adına Şamaxı Astrofizika Rəsədxanası Hüseynov R.Ə. Baki Dövlət Universiteti İsmayılov N.Z. AMEA N.Tusi adına Şamaxı Astrofizika Rəsədxanası Qasımov F. Q. AMEA Fizika İnsitutu Quluzadə C.M. Baki Dövlət Universiteti Texniki redaktor: Əsgərov A.B. İnternet səhifəsi: http://www.shao.az/AAJ Ünvan: Azərbaycan, Bakı, AZ-1001, İstiqlaliyyət küç. 10, AMEA Rəyasət Heyəti Jurnal AMEA N.Tusi adına Şamaxı Astrofizika Rəsədxanasında (www.shao.az) nəşr olunur. Мəktublar üçün: ŞAR, Azərbaycan, Bakı, AZ-1000, Mərkəzi Poçtamt, a/q №153 e-mail: [email protected] tel.: (+99412) 439 82 48 faкs: (+99412) 497 52 68 2012 Azərbaycan Milli Elmlər Akademiyası. 2012 AMEA N.Tusi adına Şamaxı Astrofizika Rəsədxanası. Bütün hüquqlar qorunmuşdur. Bakı – 2012 ____________________________________________________________________________________________________________ “Астрономический Журнал Азербайджана” Национальной Azerbaijani Astronomical Journal of the Azerbaijan National Академии Наук Азербайджана (НАНА). Academy of Sciences (ANAS) is founded in 28 Aprel 2006. Основан 28 апреля 2006 г. Web- адрес: http://www.shao.az/AAJ Online version: http://www.shao.az/AAJ Главный редактор: А.С.Гулиев Editor-in-Chief: A.S. Guliyev Заместитель главного редактора: Э.С.Бабаев Associate Editor-in-Chief: E.S. -

Optimierung Der Vorbereitung Und Auswertung Von Interferometrischen Infrarot-Beobachtungen Zirkumstellarer Scheiben
Optimierung der Vorbereitung und Auswertung von interferometrischen Infrarot-Beobachtungen zirkumstellarer Scheiben Dissertation zur Erlangung des Doktorgrades der Mathematisch-Naturwissenschaftlichen Fakult¨at der Christian-Albrechts-Universit¨at zu Kiel vorgelegt von Julia Kobus Kiel, 2021 Erster Gutachter: Prof. Dr. Sebastian Wolf Zweiter Gutachter: Prof. Dr. Wimmer-Schweingruber Tag der mundlichen¨ Prufung:¨ 13. April 2021 Zusammenfassung Protoplanetare Scheiben aus Gas und Staub sind die Geburtsst¨atten von Planeten. Die Untersuchung ihrer Eigenschaften und damit der Anfangs- und Randbedingungen fur¨ die Entstehung von Planeten ist unerl¨asslich, um Planetenentstehungsmodelle zu verbessern. Hierfur¨ sind Interferometer wie das VLTI oder ALMA besonders gut geeignet. Mit Aufl¨osungsverm¨ogen von wenigen Millibogensekunden erlauben sie es, die innerste Region nahegelegener protoplanetarer Scheiben mit einer Ausdehnung vergleichbar zur Gr¨oße unseres Sonnensystems r¨aumlich aufzul¨osen. In dieser Arbeit werden zwei Studien zu interferometrischen Beobachtungen proto- planetarer Scheiben durchgefuhrt.¨ Ausgangspunkt fur¨ die erste Studie ist die Idee, dass komplement¨are Beobachtungen mit dem VLTI-Instrument MATISSE und ALMA die Untersuchung der Verteilung des Staubes in der innersten Region protoplanetarer Scheiben erm¨oglichen sollten, da beide fur¨ Staub mit unterschiedlichen Temperaturen in unterschiedlichen Schichten der Scheibe sensitiv sind. Das Ziel der ersten Studie ist es, diesbezuglich¨ das Potential der Kombination von Beobachtungen mit MATISSE und ALMA zu beurteilen. Mithilfe von Strahlungstransportsimulationen wird der Einfluss dreier Parameter, die die Struktur der Scheibe charakterisieren, auf die mit MATISSE und ALMA beobachtbaren Gr¨oßen ermittelt. Anschließend werden die zur Einschr¨ankung der Parameter ben¨otigten Messgenauigkeiten bestimmt. Der Vergleich mit den Spezifikationen beider Instrumente zeigt, dass sich mit ALMA die radiale Struktur der Scheibe einschr¨anken l¨asst. -

Mark Blackford’S Equipment Setup for Imaging the Very Bright Binary Eta Carinae - See Mark’S Article on This New VSS Project on Page 12
Newsletter 2019-2 April 2019 www.variablestarssouth.org Mark Blackford’s equipment setup for imaging the very bright binary eta Carinae - see Mark’s article on this new VSS project on page 12. Contents From the director - Mark Blackford .............................................................................................................................................................2 Period issues in BS Mus: interim report – Tom Richards, Robert Jenkins ......................................3 An archive of Variable Star Section publications – Mati Morel ..........................................................................7 Photometry of eta Carinae – Mark Blackford...........................................................................................................................12 V777 Sag - a successful campaign – S Walker, M Blackford, EBudding ......................................13 ToMs, insights into Algolism, and the IBVS – E. Budding, D. Blane, M. G. Blackford, P. A. Reed ............................................................................................................................................................................................................................15 Two new pulsating discoveries – Mark Blackford ...........................................................................................................17 What can one do about lightning? – Greg Crawford ....................................................................................................20 Publication -
PDF Hosted at the Radboud Repository of the Radboud University Nijmegen
PDF hosted at the Radboud Repository of the Radboud University Nijmegen The following full text is a publisher's version. For additional information about this publication click this link. http://hdl.handle.net/2066/197982 Please be advised that this information was generated on 2021-10-09 and may be subject to change. Optical Variability with the Palomar Transient Factory Proefschrift ter verkrijging van de graad van doctor aan de Radboud Universiteit Nijmegen op gezag van de rector magnificus prof. dr. J.H.J.M. van Krieken, volgens besluit van het college van decanen in het openbaar te verdedigen op dinsdag 27 november 2018 om 10.30 uur precies door Joannes Christiaan Josephus van Roestel geboren op 2 april 1990 te Tilburg 525927-L-bw-van Roestel Processed on: 7-11-2018 PDF page: 1 Promotoren: Prof. dr. Paul Groot Prof. dr. Tom Prince (California Institute of Technology, VS) Manuscriptcommissie: Prof. dr. Bas van de Meerakker Prof. dr. Rudy Wijnands (Universiteit van Amsterdam) Prof. dr. Frank Verbunt Prof. dr. Peter Jonker Dr. Raffaella Margutti (Northwestern University, VS) © 2018, Jan van Roestel Optical Variability with the Palomar Transient Factory Thesis, Radboud University Nijmegen Illustrated; with bibliographic information and Dutch summary Cover design: Femke Boezen Front cover image: Binary stars Image credit: Casey Reed/NASA ISBN: 978-94-028-1279-4 525927-L-bw-van Roestel Processed on: 7-11-2018 PDF page: 2 Contents 1 Introduction 1 1.1 The optical variable sky ................................. 1 1.2 Stellar evolution; the life and death of stars . ................... 3 1.3 Binary star evolution ................................... 4 1.4 The transient zoo ....................................