Observation of a High Degree of Stopping for Laser-Accelerated Intense Proton Beams in Dense Ionized Matter
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Chinese Cities of Opportunities 2018 Report
Beijing Harbin Lanzhou Jinan Wuhan Ningbo Guangzhou Kunming Shanghai Shenyang Xi’an Qingdao Wuxi Fuzhou Shenzhen Guiyang Tianjin Dalian Taiyuan Zhengzhou Suzhou Xiamen Zhuhai Chongqing Urumqi Shijiazhuang Nanjing Hangzhou Changsha Chengdu Chinese Cities of Opportunity 2018 Cities: Creating a beautiful life and new opportunities In modern society, cities are the most Changsha-Zhuzhou-Xiangtan Region, offers a comprehensive evaluation of the important spaces in which people can the Guanzhong Plain urban cluster, competitiveness, influence and potential pursue a better life. China has the Chengdu-Chongqing Economic Zone, of urban development to provide largest urban population in the world. In the central-southern of Liaoning and benchmarks for overall urban 2017, over 58% of China’s population, or Harbin-Changchun urban cluster. development, and has come to exert an more than 800 million people, lived in People gravitate toward areas with extensive influence in China. On the cities, and the urbanisation rate for economic opportunities and high quality basis of Chinese Cities of Opportunity residents is increasing by over one public services. Therefore, enhancing 2017, the number of sample cities percentage point every year. The the inclusiveness, balance and observed this year has increased to 30, advancement of urbanisation has sustainability of the development of and special attention has been given to pushed forward the intensive and urban clusters with large cities is a the development of national strategic efficient use of resources, promoted significant undertaking at the core of regions such as Guangdong-Hong innovation and enabled the economy to resolving “the principal contradiction Kong-Macau Greater Bay Area and prosper, while providing better basic between unbalanced and inadequate Xiong’an New Area. -

Appendix 1: Rank of China's 338 Prefecture-Level Cities
Appendix 1: Rank of China’s 338 Prefecture-Level Cities © The Author(s) 2018 149 Y. Zheng, K. Deng, State Failure and Distorted Urbanisation in Post-Mao’s China, 1993–2012, Palgrave Studies in Economic History, https://doi.org/10.1007/978-3-319-92168-6 150 First-tier cities (4) Beijing Shanghai Guangzhou Shenzhen First-tier cities-to-be (15) Chengdu Hangzhou Wuhan Nanjing Chongqing Tianjin Suzhou苏州 Appendix Rank 1: of China’s 338 Prefecture-Level Cities Xi’an Changsha Shenyang Qingdao Zhengzhou Dalian Dongguan Ningbo Second-tier cities (30) Xiamen Fuzhou福州 Wuxi Hefei Kunming Harbin Jinan Foshan Changchun Wenzhou Shijiazhuang Nanning Changzhou Quanzhou Nanchang Guiyang Taiyuan Jinhua Zhuhai Huizhou Xuzhou Yantai Jiaxing Nantong Urumqi Shaoxing Zhongshan Taizhou Lanzhou Haikou Third-tier cities (70) Weifang Baoding Zhenjiang Yangzhou Guilin Tangshan Sanya Huhehot Langfang Luoyang Weihai Yangcheng Linyi Jiangmen Taizhou Zhangzhou Handan Jining Wuhu Zibo Yinchuan Liuzhou Mianyang Zhanjiang Anshan Huzhou Shantou Nanping Ganzhou Daqing Yichang Baotou Xianyang Qinhuangdao Lianyungang Zhuzhou Putian Jilin Huai’an Zhaoqing Ningde Hengyang Dandong Lijiang Jieyang Sanming Zhoushan Xiaogan Qiqihar Jiujiang Longyan Cangzhou Fushun Xiangyang Shangrao Yingkou Bengbu Lishui Yueyang Qingyuan Jingzhou Taian Quzhou Panjin Dongying Nanyang Ma’anshan Nanchong Xining Yanbian prefecture Fourth-tier cities (90) Leshan Xiangtan Zunyi Suqian Xinxiang Xinyang Chuzhou Jinzhou Chaozhou Huanggang Kaifeng Deyang Dezhou Meizhou Ordos Xingtai Maoming Jingdezhen Shaoguan -

Ancient Genomes Reveal Tropical Bovid Species in the Tibetan Plateau Contributed to the Prevalence of Hunting Game Until the Late Neolithic
Ancient genomes reveal tropical bovid species in the Tibetan Plateau contributed to the prevalence of hunting game until the late Neolithic Ningbo Chena,b,1, Lele Renc,1, Linyao Dud,1, Jiawen Houb,1, Victoria E. Mulline, Duo Wud, Xueye Zhaof, Chunmei Lia,g, Jiahui Huanga,h, Xuebin Qia,g, Marco Rosario Capodiferroi, Alessandro Achillii, Chuzhao Leib, Fahu Chenj, Bing Sua,g,2, Guanghui Dongd,j,2, and Xiaoming Zhanga,g,2 aState Key Laboratory of Genetic Resources and Evolution, Kunming Institute of Zoology, Chinese Academy of Sciences (CAS), 650223 Kunming, China; bKey Laboratory of Animal Genetics, Breeding and Reproduction of Shaanxi Province, College of Animal Science and Technology, Northwest A&F University, 712100 Yangling, China; cSchool of History and Culture, Lanzhou University, 730000 Lanzhou, China; dCollege of Earth and Environmental Sciences, Lanzhou University, 730000 Lanzhou, China; eDepartment of Earth Sciences, Natural History Museum, London SW7 5BD, United Kingdom; fGansu Provincial Institute of Cultural Relics and Archaeology, 730000 Lanzhou, China; gCenter for Excellence in Animal Evolution and Genetics, Chinese Academy of Sciences, 650223 Kunming, China; hKunming College of Life Science, University of Chinese Academy of Sciences, 100049 Beijing, China; iDipartimento di Biologia e Biotecnologie “L. Spallanzani,” Università di Pavia, 27100 Pavia, Italy; and jCAS Center for Excellence in Tibetan Plateau Earth Sciences, Institute of Tibetan Plateau Research, Chinese Academy of Sciences, 100101 Beijing, China Edited by Zhonghe Zhou, Chinese Academy of Sciences, Beijing, China, and approved September 11, 2020 (received for review June 7, 2020) Local wild bovids have been determined to be important prey on and 3,000 m a.s.l. -

Conference Program
2018 A3 Fluid Mechanics Workshop Zhejiang University, Hangzhou, China March. 9-11, 2015 Venue: Hangzhou Jinxi Hotel March 9(Friday) Conference Registration (Hangzhou Jinxi Hotel) 12:00-20:00 March 10 (Saturday) 09: 00-09: 10 Opening Chair Introduction of Zhengjiang University and Hangzhou City 09:10-09:15 Hyeong-Ohk Bae: Interaction of Particles and a Fluid 09: 15-09: 45 Jinhae Park Changhoon Lee: A new immersed boundary method for nonuniform 09: 45-10: 05 grids 10: 05-10: 35 Group photo and Tea break Hiroshi Suito: 10: 35- 11:05 Energy dissipation and streamline patterns in blood flows related to cardiovascular problems Takashi 11: 05-11: 25 Tomoki Uda: TBA Sakajo Zhenning Cai: Hermite spectral method for the homogeneous 11:25-11: 55 Boltzmann equation 12: 00-14: 00 Lunch Yue Yang: Evolution of vortex-surface fields in the transition of 14: 00-14: 30 wall-bounded flows Daegeun Yoon: An immersed boundary method with 14: 30-14: 50 Chuanju Xu improved volume conservation on a colocated grid Yanli Wang: 14: 50-15: 10 Filtered Hyperbolic Moment Method for the Vlasov Equation 15: 10-15: 40 Tea break Hirofumi Notsu: 15: 40-16: 10 Numerical analysis of the Oseen-type Peterlin viscoelastic model Yoshiki Sugitani: 16: 10-16: 30 Analysis of the immersed boundary finite element method for the Hisashi Stokes problem Okamoto Guanyu Zhou: 16: 30-16: 50 A penalty method to the Stokes-Darcy problem with a smooth interface boundary using the DG element 17: 30-19: 30 Dinner March 11(Sunday) Zhen Lei: TBA Changhoon 09: 00-09: 30 Lee Sung-Ik Sohn: Vortex shedding model and simulations for hovering 09: 30-09: 50 insects 09: 50-10: 20 Tea break Kyoko Tomoeda: 10: 20-10: 50 Mathematical analysis of suspension flowing down the inclined plane Jie Shen: A new and robust approach to construct energy stable schemes 10: 50-11: 20 Ruo Li for gradient flows Qing Chen: Unconditional energy stable numerical schemes for phase 11: 20-11: 40 field vesicle membrane model by MSAV approach. -

1 China Xi'an-Ankang Railway Construction Project
China Xi’an-Ankang Railway Construction Project (1)-(3) (CXVII-P73, CXVIII-P73, CXIX-P73) External Evaluator: Mitsue Mishima (OPMAC) Field Survey: October 2004 1. Project Profile and Japan’s ODA Loan Mongolia Beijing North Korea China South Korea Project site Xian Nepal Ankang Bhutan India Taiwan Myanmar Vietnam Laos Project site location map (Xian-Ankang, Shannxi Province) Qingcha Tunnel 1.1 Background The project site (Xian- Ankang) is located in the southern part of Shaanxi Province where the 3000-meter high Qinling Mountains extend over 1500 kilometers, and was therefore undeveloped due to difficulties in transportation and remoteness from cities. Southwest of the project site is Sichuan Province, the largest province with a population of 110 million accounting for 10% of the population of China. However, as there is no other transport route to Sichuan Province than taking a detour around the Qinling Mountains, there were only limited routes to transport energy and everyday commodities from the north. Railway transport from other regions to Sichuan Province depended on Baoching Line (Baoji-Chengdu) from the north and Xiangyu Line (Xiangfan-Ankang-Chongquing) from the east, and both lines were operating to full capacity. It was particularly difficult to double-track Baoching Line, which takes a detour to avoid the Qinling Mountains because of 1) long distance of transport, 2) large cost to transport on a gradient at an angel of 3%, and 3) the topographical problem. The opening of the electrified single track of Xian-Ankang Line not only helped increase the transport capacity within Shaanxi Province but also shortened the traveling distance to Chongquing and eased the transportation load on Baoching Line. -
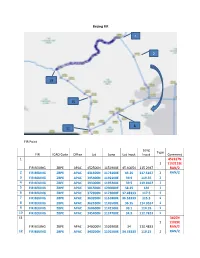
Shanghai FIR
Beijing FIR 1 2 19 15 8 11 FIR Point Long Type FIR ICAO Code Office Lat Long Lat Input Input Comment 1 452317N 1 1152115E FIR BEIJING ZBPE APAC 452500N 1151900E 45.40054 115.2947 RAN/2 2 FIR BEIJING ZBPE APAC 431500N 1173100E 43.25 117.5167 1 RAN/2 3 FIR BEIJING ZBPE APAC 395400N 1192100E 39.9 119.35 1 4 FIR BEIJING ZBPE APAC 393000N 1195200E 39.5 119.8667 1 5 FIR BEIJING ZBPE APAC 381500N 1200000E 38.25 120 1 6 FIR BEIJING ZBPE APAC 372900N 1173000E 37.48333 117.5 1 7 FIR BEIJING ZBPE APAC 363200N 1151800E 36.53333 115.3 1 8 FIR BEIJING ZBPE APAC 362100N 1145500E 36.35 114.9167 1 9 FIR BEIJING ZBPE APAC 360600N 1142100E 36.1 114.35 1 10 FIR BEIJING ZBPE APAC 345400N 1124700E 34.9 112.7833 1 11 3405N 1 11029E FIR BEIJING ZBPE APAC 340000N 1102900E 34 110.4833 RAN/2 12 FIR BEIJING ZBPE APAC 343200N 1101500E 34.53333 110.25 1 RAN/2 13 FIR BEIJING ZBPE APAC 353200N 1101800E 35.53333 110.3 1 14 FIR BEIJING ZBPE APAC 372800N 1104400E 37.46667 110.7333 1 15 FIR BEIJING ZBPE APAC 382200N 1103600E 38.36666 110.6 1 16 FIR BEIJING ZBPE APAC 384400N 1094100E 38.73333 109.6833 1 17 FIR BEIJING ZBPE APAC 402000N 1070100E 40.33333 107.0167 1 18 FIR BEIJING ZBPE APAC 404300N 1055500E 40.71667 105.9167 1 19 414451N 1 1051345E FIR BEIJING ZBPE APAC 414400N 1051300E 41.74361 105.218 RAN/2 Along political boundary to (1) Note: 1. -

Holocene Environmental Archaeology of the Yangtze River Valley in China: a Review
land Review Holocene Environmental Archaeology of the Yangtze River Valley in China: A Review Li Wu 1,2,*, Shuguang Lu 1, Cheng Zhu 3, Chunmei Ma 3, Xiaoling Sun 1, Xiaoxue Li 1, Chenchen Li 1 and Qingchun Guo 4 1 Provincial Key Laboratory of Earth Surface Processes and Regional Response in the Yangtze-Huaihe River Basin, School of Geography and Tourism, Anhui Normal University, Wuhu 241002, China; [email protected] (S.L.); [email protected] (X.S.); [email protected] (X.L.); [email protected] (C.L.) 2 State Key Laboratory of Loess and Quaternary Geology, Institute of Earth Environment, Chinese Academy of Sciences, Xi’an 710061, China 3 School of Geograpy and Ocean Science, Nanjing University, Nanjing 210023, China; [email protected] (C.Z.); [email protected] (C.M.) 4 School of Environment and Planning, Liaocheng University, Liaocheng 252000, China; [email protected] * Correspondence: [email protected] Abstract: The Yangtze River Valley is an important economic region and one of the cradles of human civilization. It is also the site of frequent floods, droughts, and other natural disasters. Conducting Holocene environmental archaeology research in this region is of great importance when studying the evolution of the relationship between humans and the environment and the interactive effects humans had on the environment from 10.0 to 3.0 ka BP, for which no written records exist. This Citation: Wu, L.; Lu, S.; Zhu, C.; review provides a comprehensive summary of materials that have been published over the past Ma, C.; Sun, X.; Li, X.; Li, C.; Guo, Q. -

Faculty Search for Zhejiang University
ADVERTISEMENT FEATURE FACULTY SEARCH FOR ZHEJIANG UNIVERSITY Located in the historical and picturesque city of Hangzhou, China, Zhejiang University is a prestigious institution of higher education with a long history. After 120 years’ development, it has become a comprehensive research university with distinctive features and great impacts at home and abroad. Research at Zhejiang University spans 12 academic disciplines, covering philosophy, economics, law, education, literature, history, art, science, engineering, agriculture, medicine and management. Of all the 22 research fi elds covered by the Essential Science Indicators (ESI), Zhejiang University has 18 fi elds listed among global top 1%, of which eight fi elds are ranked among top 1‰ in the world (ESI data, November 2017). Zhejiang University has always been committed to cultivating talents with excellence, advancing science and technology, serving social well-being and promoting advanced culture, with the spirit best manifested by the university motto “Seeking the Truth and Pioneering New Trails”. The university is dedicated to cultivating future leaders with an international perspective. Zhejiang University sincerely invites talented scholars to join and together to create a glorious future for the university and its people. ZHEJIANG UNIVERSITY ‘HUNDRED TALENTS PROGRAM’ Required qualifi cations What we o er - Demonstrated commitment to excellence in teaching and The successful candidate will be employed as a “ZJU 100 research; Young Professor”, who is qualified to supervise doctoral - A proven track record of academic achievements, which students. The university will o er: are comparable to those of assistant professors or associate - A decent compensation package; professors at a world-renowned university; - Subsidized housing available for high quality researchers to - A doctoral degree from a world-renowned university, prefer- purchase; ably with postdoctoral experiences. -

Analysis of the Spatial and Temporal Variation Characteristics of Ozone in the Pearl River Delta Region from 2016 to 2020
E3S Web of Conferences 245, 02025 (2021) https://doi.org/10.1051/e3sconf/202124502025 AEECS 2021 Analysis of the Spatial and Temporal Variation Characteristics of Ozone in the Pearl River Delta Region from 2016 to 2020 Huang Chuntao 1*, Lu Jifu 1, Liao Qifeng 2 1 Huali College, Guangdong University of Technology, Guangzhou, Guangdong, 511300 2 Guangdong Kedilong Technology Co., Ltd, Guangzhou, Guangdong, 510000 Abstract: Based on the historical data of air ozone monitoring of Pearl River Delta from 2016 to 2020, the temporal and spatial variation characteristics of ozone in the Pearl River Delta were analyzed. The results showed that the mean change curves of Q3 in the seven cities in the Pearl River Delta region from 2016 to 2020 were M-shaped, and the change trend was basically the same, except Huizhou and Zhuhai. The over standard rate of daily mean value of Q3 in Jiangmen City from 2016 to 2020 was more than 10%, and the over standard situation of daily mean value of Q3 was serious. In the Pearl River Delta region, the change trend of the monthly mean value of Q3 in the same year was basically the same. On the whole, the mean value from August to November was higher, and the mean value in June was lower. The peak of Q3 concentration appeared between 12:00 and 16:00 in the daytime, and it was generally low at night. 1 Preface studies on the spatial and temporal distribution characteristics of Q3 in the Pearl River Delta in recent Ozone (Q3) is an important component of the atmosphere, years. -

Measurements of Peroxyacetyl Nitrate at a Background Site in the Pearl River Delta Region: Production Efficiency and Regional Transport
Aerosol and Air Quality Research, 15: 833–841, 2015 Copyright © Taiwan Association for Aerosol Research ISSN: 1680-8584 print / 2071-1409 online doi: 10.4209/aaqr.2014.11.0275 Measurements of Peroxyacetyl Nitrate at a Background Site in the Pearl River Delta Region: Production Efficiency and Regional Transport 1,2 1,2* 1,2 2† 2 3 Zheng Xu , Likun Xue , Tao Wang , Tian Xia , Yuan Gao , Peter K.K. Louie , 3 Connie W.Y. Luk 1 Environment Research Institute, Shandong University, Ji’nan, Shandong, China 2 Department of Civil and Environmental Engineering, Hong Kong Polytechnic University, Hong Kong, China 3 Environmental Protection Department, the Government of Hong Kong Special Administrative Region, Hong Kong, China ABSTRACT Peroxyacetyl nitrate (PAN) is a trace constituent of the atmosphere but plays important roles in air pollution and atmospheric chemistry. To understand the chemical and transport processes of PAN in the Pearl River Delta (PRD) region, measurements of PAN, its precursors and related parameters were made at a regional background site in late summer and late autumn of 2011. Despite the fairly low ambient levels of PAN in general, several photochemical episodes with peak concentrations of PAN and ozone (O3) as high as 4.86 and 189 ppbv were observed when the region was under influence of a tropical cyclone. PAN showed a seasonal variation with higher levels in autumn than in summer. PAN production efficiency, defined as the amount of PAN formed per unit amount of nitrogen oxides (NOx) oxidized, was examined for the polluted PRD plumes, which indicated that PAN production accounted for on average approximately one third of the NOz formation. -

Lanzhou-Chongqing Railway Development – Social Action Plan Monitoring Report No
Social Monitoring Report Project Number: 35354 April 2010 PRC: Lanzhou-Chongqing Railway Development – Social Action Plan Monitoring Report No. 1 Prepared by: CIECC Overseas Consulting Co., Ltd Beijing, PRC For: Ministry of Railways This report has been submitted to ADB by the Ministry of Railways and is made publicly available in accordance with ADB’s public communications policy (2005). It does not necessarily reflect the views of ADB. ADB LOAN Social External Monitoring Report –No.1 The People’s Republic of China ADB Loan LANZHOU –CHONGQING RAILWAY PROJECT EXTERNAL MONITORING & EVALUATION OF SOCIAL DEVELOPMENT ACTION PLAN Report No.1 Prepared by CIECC OVERSEAS CONSULTING CO.,LTD April 2010 Beijing 1 CIECC OVERSEAS CONSULTING CO.,LTD TABLE OF CONTENTS 1. MONITORING AND EVALUATING OUTLINE……………………….………………………3 1.1 THE PROJECT PROMOTED SOCIAL DEVDLOPMENT ALONG THE RAILWAY OBVIOUSLY…………………………………………………..………….…3 1.2 THE PROJECT PROMOTED THE POOR PEOPLE’S INCOME AND REDUCED POVERTY……………………………………………………………...………………….5 2. PROJECT CONSTRUCTION AND SOCIAL DEVELOPMENT..……………………….6 2.1 MACRO-BENEFIT OF THE PROJECT………………...…………………………….7 2.2 THE EXTENT OF LAND ACQUISITION AND RESETTLEMENT OF PROJECT AND RESETTLEMENT RESULTS…………………………………………………....8 2.3 INFLUENCE AND PROMOTION OF PROJECT CONSTRUCTION AND LOCAL ECONOMICDEVELOPMENT………………………………………………………10 2.4 JOB OPPORTUNITY FROM THE PROJECT…………………………………… 14 2.5 PURCHASING LOCAL BUILDING MATERIALS……………………………… 16 2.6 “GREEN LONG PASSAGE” PROJECT IN PROCESS..………………………… 16 3. SAFETY MANAGEMENT IN CONSTRUCTION -

The People's Liberation Army's 37 Academic Institutions the People's
The People’s Liberation Army’s 37 Academic Institutions Kenneth Allen • Mingzhi Chen Printed in the United States of America by the China Aerospace Studies Institute ISBN: 9798635621417 To request additional copies, please direct inquiries to Director, China Aerospace Studies Institute, Air University, 55 Lemay Plaza, Montgomery, AL 36112 Design by Heisey-Grove Design All photos licensed under the Creative Commons Attribution-Share Alike 4.0 International license, or under the Fair Use Doctrine under Section 107 of the Copyright Act for nonprofit educational and noncommercial use. All other graphics created by or for China Aerospace Studies Institute E-mail: [email protected] Web: http://www.airuniversity.af.mil/CASI Twitter: https://twitter.com/CASI_Research | @CASI_Research Facebook: https://www.facebook.com/CASI.Research.Org LinkedIn: https://www.linkedin.com/company/11049011 Disclaimer The views expressed in this academic research paper are those of the authors and do not necessarily reflect the official policy or position of the U.S. Government or the Department of Defense. In accordance with Air Force Instruction 51-303, Intellectual Property, Patents, Patent Related Matters, Trademarks and Copyrights; this work is the property of the U.S. Government. Limited Print and Electronic Distribution Rights Reproduction and printing is subject to the Copyright Act of 1976 and applicable treaties of the United States. This document and trademark(s) contained herein are protected by law. This publication is provided for noncommercial use only. Unauthorized posting of this publication online is prohibited. Permission is given to duplicate this document for personal, academic, or governmental use only, as long as it is unaltered and complete however, it is requested that reproductions credit the author and China Aerospace Studies Institute (CASI).