DOCSLIB.ORG

Influence of Dispersal Processes on the Global Dynamics of Emperor

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Influence of Dispersal Processes on the Global Dynamics of Emperor Appendices: Influence of dispersal processes on the global dynamics of Emperor penguin, a species threatened by climate change. Contents A Information about the known colonies of the emperor penguin in Antarctica. 2 B Description of the metapopulation model 5 B.1 Construction of the reproduction matrix F .......................5 B.2 The dispersal model . .9 C Global sensitivity analysis 13 D Baby models 15 D.1 Case 1 and 2: dispersion to the good patch is not always optimal . 15 D.1.1 Description of local and global dynamics . 15 D.1.2 Close to the equilibrium: analytical results. 16 D.1.3 Far away from the equilibrium: numerical results. 18 D.2 Case 3: Random dispersion between poor quality habitats . 20 D.3 Implications of theoretical results for the emperor penguin . 21 E Local and regional population dynamics 23 E.1 Population size of each colony . 23 E.2 Regional population size . 26 F Isolating the colonies on the Ross Sea 31 G Random departure and random search dispersal 34 1 A Information about the known colonies of the emperor penguin in Antarctica. Table 1: Information about the known colonies of the emperor penguin in Antarctica, modified from Fretwell et al. (2012) { see the figure A.1 for a spatial repartition of the known colonies in Antarctica. # is the index of the colony used in our figures; BE is the best estimate of the observed number of breeding pairs in 2009 used in our model simulations. # name longitude latitude BE 2009 1 Snowhill -57.44 -64.52 2164 2 Dolleman -60.43 -70.61 1620 3 Smith -60.83 -74.37 4018 4 Gould -47.68 -77.71 8242 5 Luitpold -33.6 -77.077 6498 6 Dawson -26.67 -76.02 2597 7 Halley -24.4 -75.54 22510 8 Stancomb -23.09 -74.12 5455 9 Drescher -17.4 -72.83 2469 10 Riiser -15.11 -72.12 4013 11 Atka -8.13 -70.61 9657 12 Sanae -1.42 -70 3193 13 Astrid 8.31 -69.95 1368 14 Lazarev 15.55 -69.75 821 15 Ragnhild 27.15 -69.9 6870 16 Gunnerus 34.38 -68.75 4652 17 Umbeashi 43.01 -68.05 146 18 Amundsen Bay 50.55 -66.78 88 19 Kloa Point 57.28 -66.64 3283 20 Fold Island 59.32 -67.32 213 21 Taylor Glacier 60.88 -67.45 519 22 Auster 63.98 -67.39 7855 23 Cape Darnley 69.7 -67.88 3465 24 Amanda Bay 76.83 -69.27 6831 25 Haswell Island 93.01 -66.52 3247 2 Table 1 continued. # name longitude latitude BE 2009 26 Shackleton Ice Shelf 96.02 -64.86 6471 27 Bowman Island 103.07 -65.16 1609 28 Peterson Bank 110.23 -65.92 1000 29 Dibble Glacier 134.79 -66.01 12476 30 Terre Ad´elie-Pointe Geologie 140.01 -66.67 3259 31 Mertz Glacier 146.62 -66.93 4781 32 Davis Bay 158.49 -69.35 1745 33 Cape Roget 170.59 -71.99 9505 34 Coulman Island 169.61 -73.35 25298 35 Cape Washington 165.37 -74.64 11808 36 Franklin Island 168.43 -76.18 7561 37 Beaufort Island 167.02 -76.93 1641 38 Cape Crozier 169.32 -77.46 303 39 Cape Colbeck Edward VII Peninsula -157.7 -77.14 11438 40 Rupert Coast -143.3 -75.38 1550 41 Thuston Glacier Mt Siple -125.621 -73.5 2989 42 Bear Peninsula -110.25 -74.35 9457 43 Brownson Islands -103.64 -74.35 5732 44 Noville Peninsula -98.45 -71.77 3568 45 Smyley -78.83 -72.3 6061 46 Dion Islands -68.7 -67.9 0 3 Figure A.1: Spatial repartition of known colonies of Emperor penguins in Antarctica (dots). The five regional of Antarctica are shown, as well as the annual mean change of sea ice concentrations (SIC) between the 20 and 21th centuries. Modified from Jenouvrier et al. 2014. 4 B Description of the metapopulation model In this supporting information, we detail the reproduction matrix (F) and dispersal matrix (D) for our metapopulation model. Both depend on the habitat characteristics, x(t), which can change in 1 2 3 1 time (due to climate change, for instance); x := (x ; x ; x ), with x (t) := r∗(t) the realized growth rate of the local patch, x2(t) := K the carrying capacities of the patch and x3 := (dist(i; j)) the distance between patch. The population vector n, which describes the population size in each patch, is model (1): n(t + 1) = D[x; n] F[x; n] n(t): (B.1) B.1 Construction of the reproduction matrix F The local population dynamics during the reproduction phase only depend on the sub-population size ni(t) inside patch i and the habitat characteristics of that patch. Each patch is characterized by its intrinsic population growth rate ri(t), which may vary in time, and its carrying capacity, Ki, which is set to be constant over the entire time period. We assume that negative density- dependence effects occur inside good quality patches (ri(t) > 0), and they are described by a Ricker model (Ricker, 1954). On the other hand, the population tends to go extinct inside poor quality patches (r (t) 0). Thus the realized growth rate r (t) takes the form i ≤ ∗ r (t)(1 n (t)=K ) e i − i i 1 if r (t) > 0; − i ri∗(t) = 8 (B.2) > <> eri(t) 1 if r (t) 0: − i ≤ > :> The reproduction matrix is diagonal, and for any time t is Fii[x(t); n(t)] := (1 + ri∗(t)) and Fij = 0: (B.3) Estimation of the carrying capacity K. Although no effect of negative density dependence has been detected in previous studies (Jenouvrier et al., 2012), breeding space and resources are likely limited for EPs at higher population densities than the ones observed. For instance, the 5 growth of the Beaufort Island colony is limited by available space on the fast ice plate next to the island (Kooyman et al., 2007). Because data on EP populations comprise sparse counts of chicks, we cannot calculate quantitative estimates of K for EP colonies (Wienecke, 2011). Therefore, we use the stochastic population trajectories projected by a sea-ice dependent population model without density dependence (Jenouvrier et al., 2014) to derive an estimate of K as it projects the maximum population growth rate in the absence of intra-specific competition for resources. Because the distribution of the population growth rates calculated from the stochastic popula- tion trajectories is skewed by a few realizations with high growth rates, the median of the intrinsic population growth rater ¯i is different from the growth rate of the median of population size r(¯ni). The skewness of the distribution is a mathematical descriptor of second order: it does not modify the mean but changes the variance. The carrying capacity K in the Ricker model has a similar property. It modifies the dynamics at the second order because it impacts the growth rate only when the density ni is high. For each colony i and s stochastic population projections, the median of the intrinsic population growth rate is defined by n~ (t + 1) n~ (t) r¯ (t) := median i;s − i;s : i n~ (t) i;s wheren ~i;s is the population size for the s stochastic simulation for colony i. The median of the population sizen ¯i is then n¯i(t) := median n~i;s(t) : Inverting equation (B.2) in Ki and substituting ri∗ for the `observed' change in population sizes between t and t + 1, we then define the maximal carrying capacity K := max median( K r¯ (t) > 0 ); n (0) : i f i;tj i g i This estimation provides carrying capacities K which satisfy K 2n (0) on average. Figure B.1 i i ' i shows the projected global population size obtained from our metapopulation model without dis- persion using equation (B.1) withn ¯i(t) and K = 2n(0) (gray line). It agrees well with the trajectory 6 of the global population size estimated as the sum of the median of population size in each patch ¯ N(t) = i n¯i(t) obtained from the stochastic model without density dependence from Jenouvrier et al. (2014).P We can thus assume that the carrying capacities are constant over time and equal twice the number of individuals in each colony. To test the sensitivity of our results to K, Figure B.2 shows the projected global population size obtained from our metapopulation model with K = [2n(0); 3n(0); 4n(0)] for different dispersal scenarios. The case K = 4 n(0) corresponds to the maximum population size ever observed for an EP colony (see Barber-Meyer et al. (2008)). For any scenario, the global population size projected by the model have similar dynamic pattern, only the magnitude of the population size changes. x 105 2.6 2.4 2.2 2 1.8 1.6 1.4 1.2 2020 2040 2060 2080 2100 Figure B.1: Comparison of the global population size trajectory projected by a model without density dependence (Jenouvrier et al., 2014, blue dots) and our metapopulation including the carrying capacity of each patch (gray line), for a case without dispersion. 7 x 105 x 105 3 3 2.5 2.5 2 2 1.5 1.5 total population size total population size 1 1 2020 2040 2060 2080 2100 2020 2040 2060 2080 2100 time (t) time (t) (a) Short distance, K=2 (b) Long distance, K=2 x 105 x 105 3 3 2.5 2.5 2 2 1.5 1.5 total population size total population size 1 1 2020 2040 2060 2080 2100 2020 2040 2060 2080 2100 time (t) time (t) (c) Short distance, K=3 (d) Long distance, K=3 x 105 x 105 3 3 2.5 2.5 2 2 1.5 1.5 total population size total population size 1 1 2020 2040 2060 2080 2100 2020 2040 2060 2080 2100 time (t) time (t) (e) Short distance, K=4 (f) Long distance,K=4 Figure B.2: Global number of breeding pairs of emperor penguins from 2010 to 2100 for various dispersal scenarios and various carrying capacity: (a)-(b) carrying capacity K = 2n(0) that matches the population projection of a model without density-dependence (Jenouvrier et al.
Load more

Recommended publications
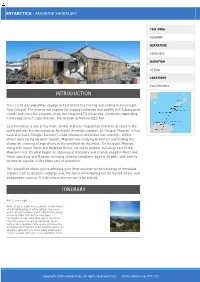
  • Introduction Itinerary
    ANTARCTICA - AKADEMIK SHOKALSKY TRIP CODE ACHEIWM DEPARTURE 10/02/2022 DURATION 25 Days LOCATIONS East Antarctica INTRODUCTION This is a 25 day expedition voyage to East Antarctica starting and ending in Invercargill, New Zealand. The journey will explore the rugged landscape and wildlife-rich Subantarctic Islands and cross the Antarctic circle into Mawsonâs Antarctica. Conditions depending, it will hope to visit Cape Denison, the location of Mawsonâs Hut. East Antarctica is one of the most remote and least frequented stretches of coast in the world and was the fascination of Australian Antarctic explorer, Sir Douglas Mawson. A true Australian hero, Douglas Mawson's initial interest in Antarctica was scientific. Whilst others were racing for polar records, Mawson was studying Antarctica and leading the charge on claiming a large chunk of the continent for Australia. On his quest Mawson, along with Xavier Mertz and Belgrave Ninnis, set out to explore and study east of the Mawson's Hut. On what began as a journey of discovery and science ended in Mertz and Ninnis perishing and Mawson surviving extreme conditions against all odds, with next to no food or supplies in the bitter cold of Antarctica. This expedition allows you to embrace your inner explorer to the backdrop of incredible scenery such as glaciers, icebergs and rare fauna while looking out for myriad whale, seal and penguin species. A truly unique journey not to be missed. ITINERARY DAY 1: Invercargill Arrive at Invercargill, New Zealand’s southernmost city. Established by Scottish settlers, the area’s wealth of rich farmland is well suited to the sheep and dairy farms that dot the landscape.
    [Show full text]
  • Potential Regime Shift in Decreased Sea Ice Production After the Mertz Glacier Calving
    ARTICLE Received 27 Jan 2012 | Accepted 3 Apr 2012 | Published 8 May 2012 DOI: 10.1038/ncomms1820 Potential regime shift in decreased sea ice production after the Mertz Glacier calving T. Tamura1,2,*, G.D. Williams2,*, A.D. Fraser2 & K.I. Ohshima3 Variability in dense shelf water formation can potentially impact Antarctic Bottom Water (AABW) production, a vital component of the global climate system. In East Antarctica, the George V Land polynya system (142–150°E) is structured by the local ‘icescape’, promoting sea ice formation that is driven by the offshore wind regime. Here we present the first observations of this region after the repositioning of a large iceberg (B9B) precipitated the calving of the Mertz Glacier Tongue in 2010. Using satellite data, we find that the total sea ice production for the region in 2010 and 2011 was 144 and 134 km3, respectively, representing a 14–20% decrease from a value of 168 km3 averaged from 2000–2009. This abrupt change to the regional icescape could result in decreased polynya activity, sea ice production, and ultimately the dense shelf water export and AABW production from this region for the coming decades. 1 National Institute of Polar Research, Tachikawa, Japan. 2 Antarctic Climate & Ecosystem Cooperative Research Centre, University of Tasmania, Hobart, Australia. 3 Institute of Low Temperature of Science, Sapporo, Japan. *These authors contributed equally to this work. Correspondence and requests for materials should be addressed to T.T. (email: [email protected]) or to G.D.W. (email: [email protected]). NATURE COMMUNICATIONS | 3:826 | DOI: 10.1038/ncomms1820 | www.nature.com/naturecommunications © 2012 Macmillan Publishers Limited.
    [Show full text]
  • A NEWS BULLETIN Published Quarterly by the NEW ZEALAND
    A N E W S B U L L E T I N p u b l i s h e d q u a r t e r l y b y t h e NEW ZEALAND ANTARCTIC SOCIETY THESE VISITORS TO LAKE FRYXELL IN THE TAYLOR VALLEY ARE LIKE DWARFS AGAINST THE TOWERING CANADA GLACIER WHICH FLOWS DOWN FROM THE ASGAARD RANGE. —Photo by R. K. McBride. Antarctic Division, D.S.I.R. September 1972 «i (Successor to "Antarctic News Bulletin") Vol. 6, No. 7 67th ISSUE Editor: H. F. GRIFFITHS, 14 Woodchester Avenue, Christchurch 1. Assistant Editor: J. M. CAFFIN, 35 Chepstow Avenue, Christchurch 5. Address all contributions, enquiries, etc., to the Editor. All Business Communications, Subscriptions, etc., to: The Secretary, New Zealand Antarctic Society, P.O. Box 1223, Christchurch, N.Z CONTENTS ARTICLES SECOND-IN-COMMAND POLAR ACTIVITIES NEW ZEALAND 222, 225, 231, 240, 243, 251, 253 U.S.A 226, 232, 252 AUSTRALIA 236 UNITED KINGDOM 234 U.S.S.R 238, 239, 241 SOUTH AFRICA 242, 250 CZECHOSLOVAKIA 235 SUB-ANTARCTIC CAMPBELL ISLAND GENERAL LONE TRIP TO POLE DISCOVERY EXPEDITION LETTERS WHALING QUOTAS FIXED ANTARCTIC BOOKSHELF Fifteen years have passed since the International Geophysical Year of 1957-58 and it might be thought that the Antarctic Continent, through the continuing research carried out by the participating nations, would by now have yielded up all its secrets. But this is a false premise; new discoveries in the various branches of science have either highlighted gaps in our knowledge or have pointed the way to investigation in new fields.
    [Show full text]
  • Amanda Bay, Ingrid Christensen Coast, Princess Elizabeth Land, East Antarctica
    MEASURE 3 - ANNEX Management Plan for Antarctic Specially Protected Area No 169 AMANDA BAY, INGRID CHRISTENSEN COAST, PRINCESS ELIZABETH LAND, EAST ANTARCTICA Introduction Amanda Bay is located on the Ingrid Christensen Coast of Princess Elizabeth Land, East Antarctica at 69°15' S, 76°49’59.9" E. (Map A). The Antarctic Specially Protected Area (ASPA) is designated to protect the breeding colony of several thousand pairs of emperor penguins annually resident in the south-west corner of Amanda Bay, while providing for continued collection of valuable long- term research and monitoring data and comparative studies with colonies elsewhere in East Antarctica. Only two other emperor penguin colonies along the extensive East Antarctic coastline are protected within ASPAs (ASPA 120, Point Géologie Archipelago and ASPA 167 Haswell Island). Amanda Bay is more easily accessed, from vessels or by vehicle from research stations in the Larsemann Hills and Vestfold Hills, than many other emperor penguin colonies in East Antarctica. This accessibility is advantageous for research purposes, but also creates the potential for human disturbance of the birds. The Antarctic coastline in the vicinity of Amanda Bay was first sighted and named the Ingrid Christensen Coast by Captain Mikkelsen in command of the Norwegian ship Thorshavn on 20 February 1935. Oblique aerial photographs of the coastline were taken by the Lars Christensen expedition in 1937 and by the US Operation Highjump in 1947 for reconnaissance purposes. In the 1954/55 summer, the Australian National Antarctic Research Expedition (ANARE) on the Kista Dan explored the waters of Prydz Bay, and the first recorded landing in the area was made by a sledging party led by Dr.
    [Show full text]
  • Species Status Assessment Emperor Penguin (Aptenodytes Fosteri)
    SPECIES STATUS ASSESSMENT EMPEROR PENGUIN (APTENODYTES FOSTERI) Emperor penguin chicks being socialized by male parents at Auster Rookery, 2008. Photo Credit: Gary Miller, Australian Antarctic Program. Version 1.0 December 2020 U.S. Fish and Wildlife Service, Ecological Services Program Branch of Delisting and Foreign Species Falls Church, Virginia Acknowledgements: EXECUTIVE SUMMARY Penguins are flightless birds that are highly adapted for the marine environment. The emperor penguin (Aptenodytes forsteri) is the tallest and heaviest of all living penguin species. Emperors are near the top of the Southern Ocean’s food chain and primarily consume Antarctic silverfish, Antarctic krill, and squid. They are excellent swimmers and can dive to great depths. The average life span of emperor penguin in the wild is 15 to 20 years. Emperor penguins currently breed at 61 colonies located around Antarctica, with the largest colonies in the Ross Sea and Weddell Sea. The total population size is estimated at approximately 270,000–280,000 breeding pairs or 625,000–650,000 total birds. Emperor penguin depends upon stable fast ice throughout their 8–9 month breeding season to complete the rearing of its single chick. They are the only warm-blooded Antarctic species that breeds during the austral winter and therefore uniquely adapted to its environment. Breeding colonies mainly occur on fast ice, close to the coast or closely offshore, and amongst closely packed grounded icebergs that prevent ice breaking out during the breeding season and provide shelter from the wind. Sea ice extent in the Southern Ocean has undergone considerable inter-annual variability over the last 40 years, although with much greater inter-annual variability in the five sectors than for the Southern Ocean as a whole.
    [Show full text]
  • Seasonal Dynamics of Totten Ice Shelf Controlled by Sea Ice Buttressing
    The Cryosphere, 12, 2869–2882, 2018 https://doi.org/10.5194/tc-12-2869-2018 © Author(s) 2018. This work is distributed under the Creative Commons Attribution 4.0 License. Seasonal dynamics of Totten Ice Shelf controlled by sea ice buttressing Chad A. Greene1, Duncan A. Young1, David E. Gwyther2, Benjamin K. Galton-Fenzi3,4, and Donald D. Blankenship1 1Institute for Geophysics, Jackson School of Geosciences, University of Texas at Austin, Austin, Texas, USA 2Institute for Marine and Antarctic Studies, University of Tasmania, Hobart, Tasmania, Australia 3Australian Antarctic Division, Kingston, Tasmania 7050, Australia 4Antarctic Climate & Ecosystems Cooperative Research Centre, University of Tasmania, Hobart, Tasmania 7001, Australia Correspondence: Chad A. Greene ([email protected]) Received: 18 April 2018 – Discussion started: 4 May 2018 Revised: 15 August 2018 – Accepted: 23 August 2018 – Published: 6 September 2018 Abstract. Previous studies of Totten Ice Shelf have em- et al., 2015). Short-term observations have identified Totten ployed surface velocity measurements to estimate its mass Glacier and its ice shelf (TIS) as thinning rapidly (Pritchard balance and understand its sensitivities to interannual et al., 2009, 2012) and losing mass (Chen et al., 2009), changes in climate forcing. However, displacement measure- but longer-term observations paint a more complex picture ments acquired over timescales of days to weeks may not ac- of interannual variability marked by multiyear periods of curately characterize long-term flow rates wherein ice veloc- ice thickening, thinning, acceleration, and slowdown (Paolo ity fluctuates with the seasons. Quantifying annual mass bud- et al., 2015; Li et al., 2016; Roberts et al., 2017; Greene et al., gets or analyzing interannual changes in ice velocity requires 2017a).
    [Show full text]
  • Antarctica: Music, Sounds and Cultural Connections
    Antarctica Music, sounds and cultural connections Antarctica Music, sounds and cultural connections Edited by Bernadette Hince, Rupert Summerson and Arnan Wiesel Published by ANU Press The Australian National University Acton ACT 2601, Australia Email: [email protected] This title is also available online at http://press.anu.edu.au National Library of Australia Cataloguing-in-Publication entry Title: Antarctica - music, sounds and cultural connections / edited by Bernadette Hince, Rupert Summerson, Arnan Wiesel. ISBN: 9781925022285 (paperback) 9781925022292 (ebook) Subjects: Australasian Antarctic Expedition (1911-1914)--Centennial celebrations, etc. Music festivals--Australian Capital Territory--Canberra. Antarctica--Discovery and exploration--Australian--Congresses. Antarctica--Songs and music--Congresses. Other Creators/Contributors: Hince, B. (Bernadette), editor. Summerson, Rupert, editor. Wiesel, Arnan, editor. Australian National University School of Music. Antarctica - music, sounds and cultural connections (2011 : Australian National University). Dewey Number: 780.789471 All rights reserved. No part of this publication may be reproduced, stored in a retrieval system or transmitted in any form or by any means, electronic, mechanical, photocopying or otherwise, without the prior permission of the publisher. Cover design and layout by ANU Press Cover photo: Moonrise over Fram Bank, Antarctica. Photographer: Steve Nicol © Printed by Griffin Press This edition © 2015 ANU Press Contents Preface: Music and Antarctica . ix Arnan Wiesel Introduction: Listening to Antarctica . 1 Tom Griffiths Mawson’s musings and Morse code: Antarctic silence at the end of the ‘Heroic Era’, and how it was lost . 15 Mark Pharaoh Thulia: a Tale of the Antarctic (1843): The earliest Antarctic poem and its musical setting . 23 Elizabeth Truswell Nankyoku no kyoku: The cultural life of the Shirase Antarctic Expedition 1910–12 .
    [Show full text]
  • Advisory Committee on Reactor Safeguards (ACRS)
    Federal Register / Vol. 77, No. 95 / Wednesday, May 16, 2012 / Notices 28903 FOR FURTHER INFORMATION CONTACT: Dates Detailed meeting agendas and meeting Polly A. Penhale at the above address or October 1, 2012 to December 30, 2012. transcripts are available on the NRC (703) 292–7420. Web site at http://www.nrc.gov/reading- Nadene G. Kennedy, rm/doc-collections/acrs. Information SUPPLEMENTARY INFORMATION: The Permit Officer, Office of Polar Programs. regarding topics to be discussed, National Science Foundation, as [FR Doc. 2012–11840 Filed 5–15–12; 8:45 am] changes to the agenda, whether the directed by the Antarctic Conservation BILLING CODE 7555–01–P meeting has been canceled or Act of 1978 (Pub. L. 95–541), as rescheduled, and the time allotted to amended by the Antarctic Science, present oral statements can be obtained Tourism and Conservation Act of 1996, from the Web site cited above or by has developed regulations for the NUCLEAR REGULATORY contacting the identified DFO. establishment of a permit system for COMMISSION Moreover, in view of the possibility that various activities in Antarctica and the schedule for ACRS meetings may be designation of certain animals and Advisory Committee on Reactor adjusted by the Chairman as necessary certain geographic areas requiring Safeguards (ACRS) Meeting of the to facilitate the conduct of the meeting, special protection. The regulations ACRS Subcommittee on Fukushima; persons planning to attend should check establish such a permit system to Notice of Meeting with these references if such designate Antarctic Specially Protected The ACRS Subcommittee on rescheduling would result in a major Areas.
    [Show full text]
  • Federal Register/Vol. 84, No. 78/Tuesday, April 23, 2019/Rules
    Federal Register / Vol. 84, No. 78 / Tuesday, April 23, 2019 / Rules and Regulations 16791 U.S.C. 3501 et seq., nor does it require Agricultural commodities, Pesticides SUPPLEMENTARY INFORMATION: The any special considerations under and pests, Reporting and recordkeeping Antarctic Conservation Act of 1978, as Executive Order 12898, entitled requirements. amended (‘‘ACA’’) (16 U.S.C. 2401, et ‘‘Federal Actions to Address Dated: April 12, 2019. seq.) implements the Protocol on Environmental Justice in Minority Environmental Protection to the Richard P. Keigwin, Jr., Populations and Low-Income Antarctic Treaty (‘‘the Protocol’’). Populations’’ (59 FR 7629, February 16, Director, Office of Pesticide Programs. Annex V contains provisions for the 1994). Therefore, 40 CFR chapter I is protection of specially designated areas Since tolerances and exemptions that amended as follows: specially managed areas and historic are established on the basis of a petition sites and monuments. Section 2405 of under FFDCA section 408(d), such as PART 180—[AMENDED] title 16 of the ACA directs the Director the tolerance exemption in this action, of the National Science Foundation to ■ do not require the issuance of a 1. The authority citation for part 180 issue such regulations as are necessary proposed rule, the requirements of the continues to read as follows: and appropriate to implement Annex V Regulatory Flexibility Act (5 U.S.C. 601 Authority: 21 U.S.C. 321(q), 346a and 371. to the Protocol. et seq.) do not apply. ■ 2. Add § 180.1365 to subpart D to read The Antarctic Treaty Parties, which This action directly regulates growers, as follows: includes the United States, periodically food processors, food handlers, and food adopt measures to establish, consolidate retailers, not States or tribes.
    [Show full text]
  • Moult of the Emperor Penguin: Travel, Location, and Habitat Selection
    MARINE ECOLOGY PROGRESS SERIES Vol. 204: 269–277, 2000 Published October 5 Mar Ecol Prog Ser Moult of the emperor penguin: travel, location, and habitat selection G. L. Kooyman1,*, E. C. Hunke2, S. F. Ackley3, R. P. van Dam1, G. Robertson4 1Scholander Hall, 0204, Scripps Institution of Oceanography, La Jolla, California 92093, USA 2MS-B216, Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA 3Cold Regions Research and Engineering Laboratory 72 Lyme Rd., Hanover, New Hampshire 03755, USA 4Australian Antarctic Division, Channel Highway, Kingston 7050, Tasmania, Australia ABSTRACT: All penguins except emperors Aptenodytes forsteri and Adelies Pygoscelis adeliae moult on land, usually near the breeding colonies. These 2 Antarctic species typically moult some- where in the pack-ice. Emperor penguins begin their moult in early summer when the pack-ice cover of the Antarctic Ocean is receding. The origin of the few moulting birds seen by observers on pass- ing ships is unknown, and the locations are often far from any known colonies. We attached satellite transmitters to 12 breeding adult A. forsteri from western Ross Sea colonies before they departed the colony for the last time before moulting. In addition, we surveyed some remote areas of the Weddell Sea north and east of some large colonies that are located along the southern and western borders of this sea. The tracked birds moved at a rate of nearly 50 km d–1 for more than 1000 km over 30 d to reach areas of perennially consistent pack-ice. Almost all birds traveled to the eastern Ross Sea and western Amundsen Sea.
    [Show full text]
  • A Case Study of Sea Ice Concentration Retrieval Near Dibble Glacier, East Antarctica
    European MSc in Marine Environment MER and Resources UPV/EHU–SOTON–UB-ULg REF: 2013-0237 MASTER THESIS PROJECT A case study of sea ice concentration retrieval near Dibble Glacier, East Antarctica: Contradicting observations between passive microwave remote sensing and optical satellites BY LAM Hoi Ming August 2016 Bremen, Germany PLENTZIA (UPV/EHU), SEPTEMBER 2016 European MSc in Marine Environment MER and Resources UPV/EHU–SOTON–UB-ULg REF: 2013-0237 Dr Manu Soto as teaching staff of the MER Master of the University of the Basque Country CERTIFIES: That the research work entitled “A case study of sea ice concentration retrieval near Dibble Glacier, East Antarctica: Contradiction between passive microwave remote sensing and optical satellite observations” has been carried out by LAM Hoi Ming in the Institute of Environmental Physics, University of Bremen under the supervision of Dr Gunnar Spreen from the of the University of Bremen in order to achieve 30 ECTS as a part of the MER Master program. In September 2016 Signed: Supervisor PLENTZIA (UPV/EHU), SEPTEMBER 2016 Abstract In East Antarctica, around 136°E 66°S, spurious appearance of polynya (open water area within an ice pack) is observed on ice concentration maps derived from the ASI (ARTIST Sea Ice) algorithm during the period of February to April 2014, using satellite data from the Advanced Microwave Scanning Radiometer 2 (AMSR-2). This contradicts with the visual images obtained by the Moderate Resolution Imaging Spectroradiometer (MODIS), which show the area to be ice covered during the period. In this study, data of ice concentration, brightness temperature, air temperature, snowfall, bathymetry, and wind in the area were analysed to identify possible explanations for the occurrence of such phenomenon, hereafter referred to as the artefact.
    [Show full text]
  • Sea Ice Extent May Have Forced Emperor Penguins Into Refugia During the Last Glacial Maximum
    Global Change Biology (2015), doi: 10.1111/gcb.12882 Too much of a good thing: sea ice extent may have forced emperor penguins into refugia during the last glacial maximum JANE L. YOUNGER1,2*, GEMMA V. CLUCAS3,4*, GERALD KOOYMAN5 , † BARBARA WIENECKE6 , ALEX D. ROGERS4 ,PHILIPN.TRATHAN7 ,TOMHART4 and † KAREN J. MILLER8,9 1Institute for Marine and Antarctic Studies, University of Tasmania, Private Bag 129, Hobart 7001 Tas., Australia, 2Australian School of Advanced Medicine, Macquarie University, 2 Technology Place, Sydney 2109 NSW, Australia, 3Ocean and Earth Sciences, University of Southampton Waterfront Campus, Southampton SO14 3ZH, UK, 4Department of Zoology, University of Oxford, South Parks Road, Oxford OX1 3PS, UK, 5Scripps Institution of Oceanography, University of California San Diego, San Diego CA, USA, 6Australian Antarctic Division, 203 Channel Highway, Kingston 7050 Tas., Australia, 7British Antarctic Survey, High Cross, Madingley Road, Cambridge CB3 0ET, UK, 8Australian Institute of Marine Science, The UWA Oceans Institute, 35 Stirling Highway, Crawley, WA 6009, Australia, 9School of Biological Sciences, University of Tasmania, Private Bag 5, Hobart 7001 Tas., Australia Abstract The relationship between population structure and demographic history is critical to understanding microevolution and for predicting the resilience of species to environmental change. Using mitochondrial DNA from extant colonies and radiocarbon-dated subfossils, we present the first microevolutionary analysis of emperor penguins (Aptenodytes forsteri) and show their population trends throughout the last glacial maximum (LGM, 19.5–16 kya) and during the subsequent period of warming and sea ice retreat. We found evidence for three mitochondrial clades within emperor penguins, suggesting that they were isolated within three glacial refugia during the LGM.
    [Show full text]