DOCSLIB.ORG

“Alan Turing: the Journey of a Racing Mind” Vali Martinez Senior Division

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
“Alan Turing: the Journey of a Racing Mind” Vali Martinez Senior Division “Alan Turing: The Journey of a Racing Mind” Vali Martinez Senior Division Individual Paper Word Count: 2,463 1 “Sometimes it is the people no one imagines anything of who do the things that no one can imagine.” 1 The Second World War persists in history as the most atrocious and utterly mortifying tragedy to befall globally. The malicious master Adolf Hitler banded with Germany, Italy, and Japan to coerce any individual set contumacious in his trail, continuously surmounting country after a helpless nation. In numerous circumstances, the advancements of the dictator's army were due to the German encryption mechanisms operating to transmit confidential combat communications. Striding forward to suffice the critical need of a penetrating mind to crack the seemingly impenetrable cryptograms, Alan Turing shined amidst the thousands that served to interpret reports from the prevalent German Enigma Machine. Turing's magnanimous wisdom drove him to vital contributions throughout the 20th-century conflict, and his lifelong benefactions to mathematics, in addition to the harsh penalty he sustained for existing as a homosexual individual, assisted in developing the position of such topics in modern-day society. Since boyhood, Turing displayed the prime demonstration of an extraordinary intellect. Born on June 23, 1912, in Maida Vale, London, the United Kingdom, the juvenile was raised with his older brother and mother (rarely witnessing the presence of his father, who was elsewhere in Chennai in the Indian Civil Service). 2 His inquisitiveness in science and biology first sparked at age ten when he received a novel with the title Nature’s Wonders . 3 His intelligence progressed throughout the stages of his youth, and he even achieved the magnificent feat of accurately condensing Einstein’s Theory of Relativity at only 15 years old. 4 In 1926, Turing attended 1 Quote said by Alan Turing, used in The Imitation Game film. 2 “ Alan Turing- BBC Horizon Documentary.” YouTube, Uploaded by documontair DH1, https://www.youtube.com/watch?v=Z-sTs2o0VuY. Accessed 25 January 2020. 3 “ Alan Turing- BBC Horizon Documentary.” YouTube, Uploaded by documontair DH1, https://www.youtube.com/watch?v=Z-sTs2o0VuY. Accessed 25 January 2020. 4 G rime, James. “Alan Turing- Celebrating the life of a genius.” YouTube, Uploaded by Cambridge University, 21 June 12th, 2 Shelbourne High School, where extensive schooling of materials such as Latin, Greek, and English literature failed to meet his demands for advanced math and science education. 5 In the early 1900s, scientific subjects were considered an improper pursuit for adolescent boys, which was why Turing's mother nudged him to study more adequate classes. 6 During his time in Shelbourne, Turing’s reserved manner often caused problems when socializing with classmates, 7 until he met Christopher Morcom. The two shared a profound passion for science and mathematics. Just as Turing began to develop feelings for his classmate, Morcom died of bovine tuberculosis, a plaguing ailment he had concealed from his companion. 8 While the discovery of Morcom’s departure left Turing in a devastated state, it motivated his investigation of consciousness and how a spirit can be present at one moment and gone the next. From that point forward, the broken boy strived to make sense of the mind and its unraveling nature. Turing advanced on to King's College in Cambridge in 1931, where he served as an undergraduate student and recognized the work of German mathematician David Hilbert and his complex Entscheidungsproblem . 9 Known to stand among the most challenging, unsolved mathematics problems of the century, the Entscheidungsproblem questioned the possibility of a method capable of determining if any given mathematical proposition could be proven . 10 The complexity of the inquiry, which included correctly defining terms such as what a ‘definite method’ https://www.youtube.com/watch?v=gtRLmL70TH0. Accessed 25 January 2020. 5 O ne school report from Alan’s headmaster at Shelbourne said, “I hope he will not fall between two stools. If he is to stay at Public School he must aim at becoming educated. If he is to be solely a scientific specialist, he is wasting his time at a Public School.” In the UK, private schools were referred to Public schools, which provided education of Latin, Greek, and literature. Turing was encouraged to attend an academy that specialized in subjects he excelled at, like mathematics and science, instead of staying at a Private school. 6 J acobson, Rebecca. “8 things you didn’t know about Alan Turing.” PBS, 28 November 2014, https://www.pbs.org/newshour/science/8-things-didnt-know-alan-turing. Accessed 23 January 2020. 7 T he Imitation Game film displays young Turing as a socially awkward boy who mostly keeps to himself, but often gets harshly bullied by other classmates. 8 Bovine tuberculosis is a chronic and contagious disease extremely rare in humans that can be caused by either inhaling infected droplets expelled by coughing or by direct contact from a wound. 9 G erman name for “decision problem”. 10 H odges, Andrew. “Alan Turing.” Stanford Encyclopedia of Philosophy, 30 September 2013, https://plato.stanford.edu/entries/turing/. Accessed 15 December 2019. 3 was or what made an ‘effective procedure’ successful, inspired Turing to devise a mechanism that would embody the most general mechanical process that could be carried out by any human. 11 This Turing Machine, intended to flawlessly capture how an active mind maneuvers, proceeded to elevate to the degree of being implemented to computable numbers . 12 While the system remained a mere simplistic vision, not intended to be physically produced, Turing recognized the importance of proving the efficiency of the Turing Machine by confirming the accuracy of its operations. 13 Nevertheless, Turing failed to establish the Entscheidungsproblem's theory in the positive; while processing an intricacy, the machine would either suspend when bestowing the solution or proceed infinitely if the resolution was absent. Referencing the example of the Entscheidungsproblem , he used the Turing Machine to come to the conclusion that one could not determine whether a machine with a given input would halt or not. 14 Acknowledged as the Halting Problem , it attested that dark areas in the world of mathematics “will always remain a barrier to complete truth.” (Grime). 15 Following his graduation from Cambridge in 1934, Turing’s mathematics degree and successful dissertation in the probability theory earned him the title of Fellowship of King’s College. 16 A fter completing his earliest triumph, On Computable Numbers, With an Application to the Entscheidungsproblem , the mathematician was admitted into Princeton University, 17 where he 11 H odges, Andrew. “Alan Turing.” Stanford Encyclopedia of Philosophy, 30 September 2013, https://plato.stanford.edu/entries/turing/. Accessed 15 December 2019. 12 S ee Appendix C. 13 H odges, Andrew. “Alan Turing.” Stanford Encyclopedia of Philosophy, 30 September 2013, https://plato.stanford.edu/entries/turing/. Accessed 15 December 2019. 14 G rime, James. “Alan Turing- Celebrating the life of a genius.” YouTube, Uploaded by Cambridge University, 21 June 12th, https://www.youtube.com/watch?v=gtRLmL70TH0. Accessed 25 January 2020. 15 G rime, James. “Alan Turing- Celebrating the life of a genius.” YouTube, Uploaded by Cambridge University, 21 June 12th, https://www.youtube.com/watch?v=gtRLmL70TH0. Accessed 25 January 2020. 16 H odges, Andrew. “Alan Turing.” Stanford Encyclopedia of Philosophy, 30 September 2013, https://plato.stanford.edu/entries/turing/. Accessed 15 December 2019. 17 H odges, Andrew. “Alan Turing.” Stanford Encyclopedia of Philosophy, 30 September 2013, https://plato.stanford.edu/entries/turing/. Accessed 15 December 2019. 4 studied as an undergraduate and completed a Ph.D. under the guidance of Alonzo Church. 18 Turing was meriting the title of “brilliant mathematician” through his meaningful participation in mathematics at just 22 years old. In the meantime, one calamitous world war began its intensification. At a previous point before the conflict, a German army clerk withdrew secret records of critical set-up instructions of the Enigma Machine. 19 The Germans had gotten a hold on an Enigma in 1928, 20 apprehending its ability to send instant messages over extended mileage during the war. The French and British's dismissal of the valuable documents caused the data to be relinquished to Polish mathematician Zvkowski Rosecki, who initiated the arduous procedure of determining how to solve the complex figure. 21 By September 1st, 1939, 22 Adolf Hitler had invaded Poland. 23 The Polish Invasion prevented the continuation of the cipher bureau's research on the Enigma, so the Polish transferred the puzzle to the British. The commenced analysis supplied the top-level cryptanalysts at Bletchley Park, the headquarters of the British code-breaking effort, a head start. 24 “This morning, the British Ambassador in Berlin handed the German Government a final note stating that unless we heard from them, by 11:00, a state of war would exist between us… This country is at war with Germany.” 25 As the proclamation of war was announced to the masses 18 A lonzo Church was an American mathematician who made significant contributions to computer science. He was Turing’s PhD advisor at Princeton, and the two co-founded the Church-Turing Thesis, which states that a problem can be effectively calculated if and only if it is computable by a Turing Machine. 19 “ Greatest Mysteries Of World War 2 Hitler’s Enigma.” YouTube , Uploaded by TheNaziGermany1945, https://www.youtube.com/watch?v=y_BL0M08-B4. Accessed 12 January 2020. 20 G rime, James. “Alan Turing and The Enigma Machine | James Grime” YouTube, Uploaded by Houston Oasis, 7 April 2019, https://www.youtube.com/watch?v=fcQMxUsYzAQ. Accessed 25 January 2020. 21 “ Greatest Mysteries Of World War 2 Hitler’s Enigma.” YouTube , Uploaded by TheNaziGermany1945, https://www.youtube.com/watch?v=y_BL0M08-B4.
Load more

Recommended publications
  • Sir Andrew J. Wiles
    ISSN 0002-9920 (print) ISSN 1088-9477 (online) of the American Mathematical Society March 2017 Volume 64, Number 3 Women's History Month Ad Honorem Sir Andrew J. Wiles page 197 2018 Leroy P. Steele Prize: Call for Nominations page 195 Interview with New AMS President Kenneth A. Ribet page 229 New York Meeting page 291 Sir Andrew J. Wiles, 2016 Abel Laureate. “The definition of a good mathematical problem is the mathematics it generates rather Notices than the problem itself.” of the American Mathematical Society March 2017 FEATURES 197 239229 26239 Ad Honorem Sir Andrew J. Interview with New The Graduate Student Wiles AMS President Kenneth Section Interview with Abel Laureate Sir A. Ribet Interview with Ryan Haskett Andrew J. Wiles by Martin Raussen and by Alexander Diaz-Lopez Allyn Jackson Christian Skau WHAT IS...an Elliptic Curve? Andrew Wiles's Marvelous Proof by by Harris B. Daniels and Álvaro Henri Darmon Lozano-Robledo The Mathematical Works of Andrew Wiles by Christopher Skinner In this issue we honor Sir Andrew J. Wiles, prover of Fermat's Last Theorem, recipient of the 2016 Abel Prize, and star of the NOVA video The Proof. We've got the official interview, reprinted from the newsletter of our friends in the European Mathematical Society; "Andrew Wiles's Marvelous Proof" by Henri Darmon; and a collection of articles on "The Mathematical Works of Andrew Wiles" assembled by guest editor Christopher Skinner. We welcome the new AMS president, Ken Ribet (another star of The Proof). Marcelo Viana, Director of IMPA in Rio, describes "Math in Brazil" on the eve of the upcoming IMO and ICM.
    [Show full text]
  • Universalization of LGBTQ Rights
    ODUMUNC 2017 Issue Brief Third Committee: Social, Humanitarian, and Cultural Universalization of LGBTQ Rights by Tiana Bailey Old Dominion University Model United Nations Society are working to extend those rights to protect Introduction individual gender identity globally. But reverse processes also can be seen. Other UN Member The question of whether and how to States have established laws to bloc such acknowledge and protect individual rights over reforms, including prohibiting public discussion gender identity is a difficult issue for the of homosexuality and trans-gender rights and international community. Although UN Member criminalizing same-sex relationships. States have dealt with this and related policy issues for hundreds of years, traditionally state policy meant persecution. Since the mid- Twentieth Century, partially in response to the persecution and killing of Fascist and Nazi governments in the 1930s and ‘40s, policy has shifted to include greater protection of their rights as equal citizens. A major issue for the international community today is whether and how to best assure those rights, whether outright universalization of LGBTQ rights is feasible, and how to achieve it. Not only are more UN Member States seeking to universalize their rights, they seek to apply them to a growing group of people. This is seen in the rising importance of the abbreviation LGBTQ, originated in the 1990s to replace what was formerly known as ‘the gay community’, and include more diverse groups. LGBTQ stands for lesbian, gay, bisexual, transgender, and queer (and/or questioning) individuals/identities. What At the worst, discrimination and persecution all share are non-heterosexual perspectives and leads to violent attacks.
    [Show full text]
  • Judith Leah Cross* Enigma: Aspects of Multimodal Inter-Semiotic
    91 Judith Leah Cross* Enigma: Aspects of Multimodal Inter-Semiotic Translation Abstract Commercial and creative perspectives are critical when making movies. Deciding how to select and combine elements of stories gleaned from books into multimodal texts results in films whose modes of image, words, sound and movement interact in ways that create new wholes and so, new stories, which are more than the sum of their individual parts. The Imitation Game (2014) claims to be based on a true story recorded in the seminal biography by Andrew Hodges, Alan Turing: The Enigma (1983). The movie, as does its primary source, endeavours to portray the crucial role of Enigma during World War Two, along with the tragic fate of a key individual, Alan Turing. The film, therefore, involves translation of at least two “true” stories, making the film a rich source of data for this paper that addresses aspects of multimodal inter-semiotic translations (MISTs). Carefully selected aspects of tales based on “true stories” are interpreted in films; however, not all interpretations possess the same degree of integrity in relation to their original source text. This paper assumes films, based on stories, are a form of MIST, whose integrity of translation needs to be assessed. The methodology employed uses a case-study approach and a “grid” framework with two key critical thinking (CT) standards: Accuracy and Significance, as well as a scale (from “low” to “high”). This paper offers a stretched and nuanced understanding of inter-semiotic translation by analysing how multimodal strategies are employed by communication interpretants. Keywords accuracy; critical thinking; inter-semiotic; multimodal; significance; translation; truth 1.
    [Show full text]
  • Timeline of Computer History
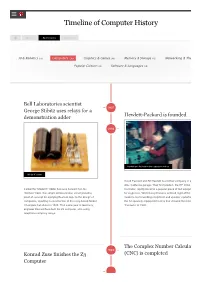
    Timeline of Computer History By Year By Category Search AI & Robotics (55) Computers (145)(145) Graphics & Games (48) Memory & Storage (61) Networking & The Popular Culture (50) Software & Languages (60) Bell Laboratories scientist 1937 George Stibitz uses relays for a Hewlett-Packard is founded demonstration adder 1939 Hewlett and Packard in their garage workshop “Model K” Adder David Packard and Bill Hewlett found their company in a Alto, California garage. Their first product, the HP 200A A Called the “Model K” Adder because he built it on his Oscillator, rapidly became a popular piece of test equipm “Kitchen” table, this simple demonstration circuit provides for engineers. Walt Disney Pictures ordered eight of the 2 proof of concept for applying Boolean logic to the design of model to test recording equipment and speaker systems computers, resulting in construction of the relay-based Model the 12 specially equipped theatres that showed the movie I Complex Calculator in 1939. That same year in Germany, “Fantasia” in 1940. engineer Konrad Zuse built his Z2 computer, also using telephone company relays. The Complex Number Calculat 1940 Konrad Zuse finishes the Z3 (CNC) is completed Computer 1941 The Zuse Z3 Computer The Z3, an early computer built by German engineer Konrad Zuse working in complete isolation from developments elsewhere, uses 2,300 relays, performs floating point binary arithmetic, and has a 22-bit word length. The Z3 was used for aerodynamic calculations but was destroyed in a bombing raid on Berlin in late 1943. Zuse later supervised a reconstruction of the Z3 in the 1960s, which is currently on Operator at Complex Number Calculator (CNC) display at the Deutsches Museum in Munich.
    [Show full text]
  • Román Ceano © Román Ceano
    La máquina enigma Román Ceano © Román Ceano. Todos los derechos reservados. El libro fue compilado de http://www.kriptopolis.org/enigma La fotografía sacada de http://enigma.wikispaces.com/file/view/enigma.jpg/30598271 Preludio En el verano de 1938, una pequeña localidad del condado de Buckingham vio perturbada su tranquilidad por la llegada de unos estrafalarios visitantes. Se trataba de hombres de aspecto próspero pero descuidado, acompañados por chicas que los lugareños juzgaron sospechosamente guapas y alegres. Estaban dirigidos al parecer por un tal Capitán Ridley, y decían que el motivo de su presencia era la caza. Ninguna de las camareras que les servían la cena en los hotelitos de la zona les oyó comentar anécdota cinegética alguna, lo cual era congruente con el hecho de que faltaban meses para la temporada. Lo que sí les oyeron comentar eran los opíparos almuerzos con que se obsequiaban. Estos debían tener lugar en la propiedad llamada Bletchley Park, puesto que allí se dirigían todos en sus coches cada mañana y de allí volvían cada tarde. Todo el mundo en Bletchley conocía la finca, sin duda la mejor de la comarca. La había creado sesenta años antes un exitoso corredor de bolsa de Londres llamado Herbert Leon, deseoso de disfrutar de la vida rural de las clases altas victorianas. Presidía la finca una mansión cuya fachada lucía una grotesca mezcla de estilos, que imitaba los palacios de las grandes familias rurales que habían sido reformados varias veces durante centurias. En la parte trasera había un gran patio, separado del edificio principal, donde estaban las cuadras, una enorme despensa donde guardar fruta fresca para el invierno y varias edificaciones auxiliares que recreaban de manera muy fidedigna el centro de operaciones de una propiedad rural.
    [Show full text]
  • Alan Turing, Computing, Bletchley, and Mathematics, Wellington Public
    Alan Turing, Computing, Bletchley, and Mathematics Rod Downey Victoria University Wellington New Zealand Downey's research is supported by the Marsden Fund, and this material also by the Newton Institute. Wellington, February 2015 Turing I Turing has become a larger than life figure following the movie \The Imitation Game". I which followed Andrew Hodges book \Alan Turing : The Enigma", I which followed the release of classified documents about WWII. I I will try to comment on aspects of Turing's work mentioned in the movie. I I will give extensive references if you want to follow this up, including the excellent Horizon documentary. I Posted to my web site. Type \rod downey" into google. Turing Award I The equivalent of the \Nobel Prize" in computer science is the ACM Turing Award. I It is for life work in computer science and worth about $1M. I Why? This award was made up (1966) was well before Bletchley became public knowledge. I (Aside) Prof. D. Ritchie (Codebreaker)-from \Station X, Pt 3" Alan Turing was one of the figures of the century. || There were great men at Bletchley Park, but in the long hall of history Turing's name will be remembered as Number One in terms of consequences for mankind. Logic I Aristotle and other early Greeks then \modern" re-invention: Leibnitz (early 18th C), Boole, Frege, etc. I We want a way to represent arguments, language, processes etc by formal symbols and manipulate them like we do numbers to determine, e.g. validity of argument. I Simplest modern formal system propositional logic.
    [Show full text]
  • The Essential Turing Reviewed by Andrew Hodges
    Book Review The Essential Turing Reviewed by Andrew Hodges The Essential Turing the Second World War, with particular responsibility A. M. Turing, B. Jack Copeland, ed. for the German Enigma-enciphered naval commu- Oxford University Press, 2004 nications, though this work remained secret until US$29.95, 662 pages the 1970s and only in the 1990s were documents ISBN 0198250800 from the time made public. Many mathematicians would see Turing as a The Essential Turing is a selection of writings of the hero for the 1936 work alone. But he also makes a British mathematician Alan M. Turing (1912–1954). striking exemplar of mathematical achievement in Extended introductions and annotations are added his breadth of attack. He made no distinction be- by the editor, the New Zealand philosopher B. Jack tween “pure” and “applied” and tackled every kind Copeland, and there are some supplementary pa- of problem from group theory to biology, from ar- pers and commentaries by other authors. Alan Tur- guing with Wittgenstein to analysing electronic ing was the founder of the theory of computabil- component characteristics—a strategy diametri- ity, with his paper “On Computable numbers, with cally opposite to today’s narrow research training. an application to the Entscheidungsproblem” (Tur- The fact that few had ever heard of him when he ing 1936). This, a classic breakthrough of twenti- died mysteriously in 1954, and that his work in de- eth century mathematics, was written when he was feating Nazi Germany remained unknown for so twenty-three. In the course of this work in mathe- long, typifies the unsung creative power of math- matical logic, he defined the concept of the uni- ematics which the public—indeed our own stu- versal machine.
    [Show full text]
  • 50 Note Character Selection Announcement
    £50 note character selection announcement Speech given by Mark Carney Governor of the Bank of England Science and Industry Museum, Manchester 15 July 2019 I am grateful to Clare Macallan for her assistance in preparing these remarks, and to Matthew Corder, Toby Davies, Sarah John, Elizabeth Levett, Debbie Marriott and James Oxley for their help with background research and analysis. 1 All speeches are available online at www.bankofengland.co.uk/news/speeches It’s a pleasure to be at the Science and Industry Museum in Manchester. These galleries testify to the UK’s rich history of discovery in science, technology and industry. A little more than eight months ago, the Bank sought to recognise the UK’s extraordinary scientific heritage by asking people across the country to “Think Science” in order to help us choose the character to feature on the new £50 note. We were overwhelmed by the response. In six weeks, almost a quarter of a million nominations were submitted, from which we distilled a very long list of nearly 1,000 unique characters.1 The hard work of narrowing down these names to a shortlist of twelve options required the incomparable knowledge and tireless work of the Banknote Character Advisory Committee.2 On behalf of the Bank, I would like to thank the external members of the Advisory Committee – Dr Maggie Aderin-Pocock, Dr Emily Grossman, Professor Simon Schaffer, Dr Simon Singh, Professor Sir David Cannadine, Sandy Nairne and Baroness Lola Young – for their invaluable expert advice and unbridled enthusiasm. The characters that made it through to the final shortlist were: Mary Anning Charles Babbage and Ada Lovelace Paul Dirac Rosalind Franklin Stephen Hawking Caroline Herschel and William Herschel Dorothy Hodgkin James Clerk Maxwell Srinivasa Ramanujan Ernest Rutherford Frederick Sanger Alan Turing The shortlist epitomises the breadth and depth of scientific achievement in the UK.
    [Show full text]
  • The Essential Turing: Seminal Writings in Computing, Logic, Philosophy, Artificial Intelligence, and Artificial Life: Plus the Secrets of Enigma
    The Essential Turing: Seminal Writings in Computing, Logic, Philosophy, Artificial Intelligence, and Artificial Life: Plus The Secrets of Enigma B. Jack Copeland, Editor OXFORD UNIVERSITY PRESS The Essential Turing Alan M. Turing The Essential Turing Seminal Writings in Computing, Logic, Philosophy, Artificial Intelligence, and Artificial Life plus The Secrets of Enigma Edited by B. Jack Copeland CLARENDON PRESS OXFORD Great Clarendon Street, Oxford OX2 6DP Oxford University Press is a department of the University of Oxford. It furthers the University’s objective of excellence in research, scholarship, and education by publishing worldwide in Oxford New York Auckland Cape Town Dar es Salaam Hong Kong Karachi Kuala Lumpur Madrid Melbourne Mexico City Nairobi New Delhi Taipei Toronto Shanghai With offices in Argentina Austria Brazil Chile Czech Republic France Greece Guatemala Hungary Italy Japan South Korea Poland Portugal Singapore Switzerland Thailand Turkey Ukraine Vietnam Published in the United States by Oxford University Press Inc., New York © In this volume the Estate of Alan Turing 2004 Supplementary Material © the several contributors 2004 The moral rights of the author have been asserted Database right Oxford University Press (maker) First published 2004 All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, without the prior permission in writing of Oxford University Press, or as expressly permitted by law, or under terms agreed with the appropriate reprographics rights organization. Enquiries concerning reproduction outside the scope of the above should be sent to the Rights Department, Oxford University Press, at the address above.
    [Show full text]
  • Joan Clarke at Station X
    Joan Clarke at Station X Before Joan Clarke worked at Bletchley Park’s Hut 8, she already knew Alan Turing. He was a friend of Joan’s brother. A very intelligent young woman, Joan studied mathematics at Cambridge University’s Newnham College. Gordon Welchman, who was working for the Government Code & Cypher School in the late 1930s, recruited Joan to work at Bletchley Park. He’d been her Geometry supervisor at Cambridge. At the time, women did not typically fill important jobs at Bletchley Park (or anywhere else throughout Britain). So ... at the beginning of her work at Station X ... Joan filled a clerical slot. It took very little time, however, for Joan to get her “own table” inside Hut 8. This promotion effectively placed her on Turing’s code-breaking team. Not only did Joan do great work at Bletchley, by 1944 she was deputy-head of the Hut-8 team. During the early part of her work at Station X, Joan had been promoted to a “Linguist,” even though she wasn’t fluent in other languages. (It was just a way for her to receive better pay for her work.) She once answered a questionnaire with these words: Grade: Linguist, Languages: None. When she first became a Hut-8 code breaker, Joan worked with Alan Turing, Tony Kendrick and Peter Twinn. Their actual work focused on breaking Germany’s Naval Enigma code (which the Station X workers had codenamed “Dolphin”). Joan and Alan Turing became very close friends and, in 1941, the head of Hut 8 asked his friend to become his wife.
    [Show full text]
  • Simply Turing
    Simply Turing Simply Turing MICHAEL OLINICK SIMPLY CHARLY NEW YORK Copyright © 2020 by Michael Olinick Cover Illustration by José Ramos Cover Design by Scarlett Rugers All rights reserved. No part of this publication may be reproduced, distributed, or transmitted in any form or by any means, including photocopying, recording, or other electronic or mechanical methods, without the prior written permission of the publisher, except in the case of brief quotations embodied in critical reviews and certain other noncommercial uses permitted by copyright law. For permission requests, write to the publisher at the address below. [email protected] ISBN: 978-1-943657-37-7 Brought to you by http://simplycharly.com Contents Praise for Simply Turing vii Other Great Lives x Series Editor's Foreword xi Preface xii Acknowledgements xv 1. Roots and Childhood 1 2. Sherborne and Christopher Morcom 7 3. Cambridge Days 15 4. Birth of the Computer 25 5. Princeton 38 6. Cryptology From Caesar to Turing 44 7. The Enigma Machine 68 8. War Years 85 9. London and the ACE 104 10. Manchester 119 11. Artificial Intelligence 123 12. Mathematical Biology 136 13. Regina vs Turing 146 14. Breaking The Enigma of Death 162 15. Turing’s Legacy 174 Sources 181 Suggested Reading 182 About the Author 185 A Word from the Publisher 186 Praise for Simply Turing “Simply Turing explores the nooks and crannies of Alan Turing’s multifarious life and interests, illuminating with skill and grace the complexities of Turing’s personality and the long-reaching implications of his work.” —Charles Petzold, author of The Annotated Turing: A Guided Tour through Alan Turing’s Historic Paper on Computability and the Turing Machine “Michael Olinick has written a remarkably fresh, detailed study of Turing’s achievements and personal issues.
    [Show full text]
  • Speech by Sarah John at the Royal Institution, London, on Tuesday 16
    Science and banknotes Remarks given by Sarah John, Chief Cashier The Royal Institution 16 July 2019 I would like to thank Elizabeth Levett, Gareth Pearce and Emma Sinclair for their help in preparing the text. 1 All speeches are available online at www.bankofengland.co.uk/news/speeches I’m delighted to be here this evening to explore the links between science and banknotes, a topic which seems even more appropriate the day after we announced the great scientist Alan Turing will be celebrated on the new £50 note. I am also pleased to be here in a personal capacity. As Chief Cashier with responsibility for our banknotes it is a peculiar honour to be able to speak in a room that has featured on one of those notes – as this very lecture theatre did on the £20 note, which depicted Michael Faraday, who himself often lectured here. Though thanks to a quirk in that note's design I can say for sure I am not the first Bank of England staff member to be pictured here; a section of the audience in the Faraday note are minute portraits of the then banknote design team, one of whom is still working at the Bank. As far as I'm aware he has yet to find a way to include himself in any of our other banknote designs – including the design we unveiled yesterday for the next £50 note featuring Alan Turing. As the central bank of the United Kingdom we have a wide range of responsibilities such as setting interest rates, regulating banks, setting rules for the financial system and storing gold.
    [Show full text]