Solid State Physics for the Structure of Uranium Oxide and Zinc Arsenide
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Measurement of Uranium Dioxide Thermophysical Properties by the Laser Flash Method
2009 International Nuclear Atlantic Conference - INAC 2009 Rio de Janeiro,RJ, Brazil, September27 to October 2, 2009 ASSOCIAÇÃO BRASILEIRA DE ENERGIA NUCLEAR - ABEN ISBN: 978-85-99141-03-8 MEASUREMENT OF URANIUM DIOXIDE THERMOPHYSICAL PROPERTIES BY THE LASER FLASH METHOD Pablo Andrade Grossi 1, Ricardo Alberto Neto Ferreira 2, Denise das Mercês Camarano 3, Roberto Márcio de Andrade 4 1,2,3 Centro de Desenvolvimento da Tecnologia Nuclear-CDTN Comissão Nacional de Energia Nuclear-CNEN Av. Presidente Antônio Carlos 6627 Cidade Universitária-Pampulha-Caixa Postal 941 CEP: 31.161-970 Belo Horizonte, MG 1 [email protected] 2 [email protected] 3 [email protected] 4 Departamento de Engenharia Mecânica Escola de Engenharia da Universidade Federal de Minas Gerais Av. Presidente Antônio Carlos 6627-Cidade Universitária-Pampulha CEP: 31.270-901 - Belo Horizonte – MG - Brasil 4 [email protected] ABSTRACT The evaluation of the thermophysical properties of uranium dioxide (UO 2), including a reliable uncertainty assessment, are required by the nuclear reactor design. These important informations are used by thermohydraulic codes to define operational aspects and to assure the safety, when analyzing various potential situations of accident. The Laser Flash Method had become the most popular method to measure the thermophysical properties of materials. Despite its several advantages, some experimental obstacles have been found due to the difficulty to obtain experimentally the ideals initial and boundary conditions required by the original method. An experimental apparatus and a methodology for estimating uncertainties of thermal diffusivity, thermal conductivity and specific heat measurements based on the Laser Flash Method are presented. A stochastic thermal diffusion modeling has been developed and validated by Standard Samples. -

Depleted Uranium Technical Brief
Disclaimer - For assistance accessing this document or additional information,please contact [email protected]. Depleted Uranium Technical Brief United States Office of Air and Radiation EPA-402-R-06-011 Environmental Protection Agency Washington, DC 20460 December 2006 Depleted Uranium Technical Brief EPA 402-R-06-011 December 2006 Project Officer Brian Littleton U.S. Environmental Protection Agency Office of Radiation and Indoor Air Radiation Protection Division ii iii FOREWARD The Depleted Uranium Technical Brief is designed to convey available information and knowledge about depleted uranium to EPA Remedial Project Managers, On-Scene Coordinators, contractors, and other Agency managers involved with the remediation of sites contaminated with this material. It addresses relative questions regarding the chemical and radiological health concerns involved with depleted uranium in the environment. This technical brief was developed to address the common misconception that depleted uranium represents only a radiological health hazard. It provides accepted data and references to additional sources for both the radiological and chemical characteristics, health risk as well as references for both the monitoring and measurement and applicable treatment techniques for depleted uranium. Please Note: This document has been changed from the original publication dated December 2006. This version corrects references in Appendix 1 that improperly identified the content of Appendix 3 and Appendix 4. The document also clarifies the content of Appendix 4. iv Acknowledgments This technical bulletin is based, in part, on an engineering bulletin that was prepared by the U.S. Environmental Protection Agency, Office of Radiation and Indoor Air (ORIA), with the assistance of Trinity Engineering Associates, Inc. -

(12) United States Patent (10) Patent No.: US 8,333,879 B2 M00re Et Al
US0083.33879B2 (12) United States Patent (10) Patent No.: US 8,333,879 B2 M00re et al. (45) Date of Patent: Dec. 18, 2012 (54) ELECTRODEPOSITION OF DELECTRIC (56) References Cited COATINGS ON SEMCONDUCTIVE SUBSTRATES U.S. PATENT DOCUMENTS 3,455,806 A 7/1969 Spoor et al. (75) Inventors: Kelly L. Moore, Dunbar, PA (US); 3,663,389 A 5, 1972 Koral et al. Michael J. Pawlik, Glenshaw, PA (US); 3,749,657 A 7, 1973 Le Bras et al. Michael G. Sandala, Pittsburgh, PA 3,793,278 A 2f1974 De Bona (US); Craig A. Wilson, Allison Park, PA 3,928, 157 A 12/1975 Suematsu et al. 3,947.338 A 3, 1976 Jerabek et al. (US) 3,947,339 A 3, 1976 Jerabek et al. 3,962,165 A 6, 1976 Bosso et al. (73) Assignee: PPG Industries Ohio, Inc., Cleveland, 3,975,346 A 8, 1976 Bosso et al. OH (US) 3,984,299 A 10, 1976 Jerabek (*) Notice: Subject to any disclaimer, the term of this (Continued) patent is extended or adjusted under 35 FOREIGN PATENT DOCUMENTS U.S.C. 154(b) by 0 days. EP OO12463 A1 6, 1980 (21) Appl. No.: 13/240,455 OTHER PUBLICATIONS (22) Filed: Sep. 22, 2011 Kohler, E. P. "An Apparatus for Determining Both the Quantity of Gas Evolved and the Amount of Reagent Consumed in Reactions (65) Prior Publication Data with Methyl Magnesium Iodide'. J. Am. Chem. Soc., 1927, 49 (12), US 2012/OOO6683 A1 Jan. 12, 2012 3181-3188, American Chemical Society, Washington, D.C. Related U.S. -

Safety Data Sheet
SAFETY DATA SHEET Revision Date 29-Jun-2018 Revision Number 1 SECTION 1: IDENTIFICATION OF THE SUBSTANCE/MIXTURE AND OF THE COMPANY/UNDERTAKING 1.1. Product identification Product Description: Cadmium arsenide Cat No. : 22773 CAS-No 12006-15-4 Molecular Formula As2 Cd3 1.2. Relevant identified uses of the substance or mixture and uses advised against Recommended Use Laboratory chemicals. Uses advised against No Information available 1.3. Details of the supplier of the safety data sheet Company Alfa Aesar . Avocado Research Chemicals, Ltd. Shore Road Port of Heysham Industrial Park Heysham, Lancashire LA3 2XY United Kingdom Office Tel: +44 (0) 1524 850506 Office Fax: +44 (0) 1524 850608 E-mail address [email protected] www.alfa.com Product Safety Department 1.4. Emergency telephone number Call Carechem 24 at +44 (0) 1865 407333 (English only); +44 (0) 1235 239670 (Multi-language) SECTION 2: HAZARDS IDENTIFICATION 2.1. Classification of the substance or mixture CLP Classification - Regulation (EC) No 1272/2008 Physical hazards Based on available data, the classification criteria are not met Health hazards Acute oral toxicity Category 3 (H301) Acute Inhalation Toxicity - Dusts and Mists Category 2 (H330) Environmental hazards ______________________________________________________________________________________________ ALFAA22773 Page 1 / 10 SAFETY DATA SHEET Cadmium arsenide Revision Date 29-Jun-2018 ______________________________________________________________________________________________ Acute aquatic toxicity Category 1 (H400) Chronic -

High-Density Concrete with Ceramic Aggregate Based on Depleted Uranium Dioxide
HIGH-DENSITY CONCRETE WITH CERAMIC AGGREGATE BASED ON DEPLETED URANIUM DIOXIDE S.G. Ermichev, V.I. Shapovalov, N.V.Sviridov (RFNC-VNIIEF, Sarov, Russia) V.K. Orlov, V.M. Sergeev, A. G. Semyenov, A.M. Visik, A.A. Maslov, A. V. Demin, D.D. Petrov, V.V. Noskov, V. I. Sorokin, O. I. Uferov (VNIINM, Moscow, Russia) L. Dole (ORNL, Oak Ridge, USA) Abstract - Russia is researching the production and testing of concretes with ceramic aggregate based on depleted uranium dioxide (UO2). These DU concretes are to be used as structural and radiation-shielded material for casks for A-plant spent nuclear fuel transportation and storage. This paper presents the results of studies aimed at selection of ceramics and concrete composition, justification of their production technology, investigation of mechanical properties, and chemical stability. This Project is being carried out at the A.A. Bochvar All-Russian Scientific-Research Institute of inorganic materials (VNIINM, Russia) and Russian Federal Nuclear Center – All-Russia Scientific Research Institute of Experimental Physics (RFNC-VNIIEF, Russia). This Project #2691 is financed by the International Science and Technology Center (ISTC) under collaboration of the Oak- Ridge National Laboratory (USA) I. INTRODUCTION The current practice of ensuring the required gamma conduction, thermo-, radiation and corrosion resistance, shielding and strength of metal-concrete casks is based on service life and water resistance. concrete density. For this purpose high-density rocks Specific characteristics of UO2’s chemical activity (magnetite, iron glance, barium sulfate, etc.) as well as because of its small size of particles and thus great specific scrap, scale, broken metal chips and others are introduced surface area prevent the use of traditional methods of UO2 into concrete as coarse aggregates. -

I -F??TI O08'w –Gçanooog –Ggan
Feb. 27, 1962 L. BURRIS, JR., ETA 3,023,097 REPROCESSING URANIUM DIOXDE FUES Filed Nov. 23, 1959 2 Sheets-Sheet I-F??TI OOOG–ggan O08’w–gçan no?opa8 (g?20%OG) INVENTOR. Les lie 8urris, Jr. Af r e di S c h n e i der Attorney Feb. 27, 1962 L. BURRIS, JR., ETA 3,023,097 REPROCESSING URANIUM DIOXDE FUELS Filed Nov. 23, 1959 2 Sheets-Sheet 2 - 4O - 5 ? - 6 O - 8O - 9 O - OO - , ? - 2 O - 3 O Nd 2O Gnd Sm2O3 - 4 O - 150 Pr2O3 and Ce2O3 O 3OO 5OO IOOO 5OO 2OOO 25 OO Temperature (K) F I Leslie Burris,INVENTOR. Jr. Alfred Schneid er BY ????? C???-e Attorney - 3,023,097 United States Patent Office Patented Feb. 27, 1962 2 of the dioxide fuel and its commingled substances in prep 3,323,097 aration for the next step about to be described; this size REPROCESSING GUARNUM DIXE FUELS Lesie Burris, Jr., and Alfred Schneider, Naperville, H., reduction is best carried out by successive oxidations and aSsigi nors to the United States of America as rere reductions which cause crumbling by reason of the suc sented by the United States Atomic Energy Cons cessive changes in crystal structure. After the particle ?$$??? size has been reduced sufficiently, a molten reducing i Fied Nov. 23, 1959, Ser. No. 854,989 metal of the group consisting of zinc and cadmium is 4 Claims. (C. 75-84.) introduced to the crumbled mixture, and this causes quite a number of metals to go into the metallic state, where The invention relates to a novel pyrometalurgical O upon they alloy with the reducing metal and the molten method of reprocessing uranium dioxide fuels after they metal phase may then be separated from the solid oxide have become contaminated by ª fission products in i nu phase consisting of the oxides of metals such as uranium, clear reactors, and more particularly, to a novel method rare earths and plutonium which are still not reduced. -

Dissolution of Uranium Dioxide in Nitric Acid Media: What Do We Know?
EPJ Nuclear Sci. Technol. 3, 13 (2017) Nuclear © Sciences P. Marc et al., published by EDP Sciences, 2017 & Technologies DOI: 10.1051/epjn/2017005 Available online at: http://www.epj-n.org REGULAR ARTICLE Dissolution of uranium dioxide in nitric acid media: what do we know? Philippe Marc1, Alastair Magnaldo1,*, Aimé Vaudano1, Thibaud Delahaye2, and Éric Schaer3 1 CEA, Nuclear Energy Division, Research Department of Mining and Fuel Recycling Processes, Service of Dissolution and Separation Processes, Laboratory of Dissolution Studies, 30207 Bagnols-sur-Cèze, France 2 CEA, Nuclear Energy Division, Research Department of Mining and Fuel Recycling Processes, Service of Actinides Materials Fabrication, Laboratory of Actinide Conversion Processes, 30207 Bagnols-sur-Cèze, France 3 Laboratoire Réactions et Génie des Procédés, UMR CNRS 7274, University of Lorraine, 54001 Nancy, France Received: 16 March 2016 / Received in final form: 15 November 2016 / Accepted: 14 February 2017 Abstract. This article draws a state of knowledge of the dissolution of uranium dioxide in nitric acid media. The chemistry of the reaction is first investigated, and two reactions appear as most suitable to describe the mechanism, leading to the formation of monoxide and dioxide nitrogen as reaction by-products, while the oxidation mechanism is shown to happen before solubilization. The solid aspect of the reaction is also investigated: manufacturing conditions have an impact on dissolution kinetics, and the non-uniform attack at the surface of the solid results in the appearing of pits and cracks. Last, the existence of an autocatalytic mechanism is questionned. The second part of this article presents a compilation of the impacts of several physico-chemical parameters on the dissolution rates. -
Experimental Studies of Neutron Irradiated Uranium Dioxide at High Temperatures
NL90C1051 lNIS-mi— 12739 Experimental studies of neutron irradiated uranium dioxide at high temperatures R.H.J. Tanke EXPERIMENTAL STUDIES OF NEUTRON IRRADIATED URANIUM DIOXIDE AT HIGH TEMPERATURES EXPERIMENTELE STUDIES VAN MET NEUTRONEN BESTRAALD URANIUMDIOXIDE BIJ HOGE TEMPERATUREN (met een samenvatting in het Nederlands) PROEFSCHRIFT TER VERKRIJGING VAN DE GRAAD VAN DOCTOR AAN DE RIJKSUNIVERSITEIT TE UTRECHT, OP GEZAG VAN DE RECTOR MAGNIFICUS PROF.DR. J.A. VAN GÏNKEL, VOLGENS BESLUIT VAN HET COLLEGE VAN DEKANEN IN HET OPENBAAR TE VERDEDIGEN OP WOENSDAG 20 JUNI 1990 DES NAMIDDAGS TE 4.15 UUR. door Richardus Hendrikus Johannes Tanke geboren op 19 april 1957 te Hengelo (O) Promotor: Prof.Dr. CD. Andriesse Aan Pien CIP-GEGEVENS KONINKLIJKE BIBLIOTHEEK DEN HAAG Tanke, Richardus Hend. ^kus Johannes Experimental studies of neutron irradiated uranium dioxide at high temperatures / Richardus Hendrikus Johannes Tanke. - Arnhem : KEMA. - 111. Thesis Utrecht. - With index, ref. - With summary in Dutch. ISBN 90-353-1023-3 pbk. ISBN 90-353-1024-1 geb. SISO 538 UDC [539.125.06:546.791-31:536.45](043.3) Subject headings: uranium dioxide / gamma tomography. Contents Summary and outline 7 Outline of this thesis 9 Chapter 1: Introduction 11 The safety issue during the development of nuclear power 11 Experimental programmes on the release of fission products 15 from overheated fuel The KEMA source term experiment 17 References 18 Chapter 2: Experimental equipment and laboratory facilities 21 The hot cell 23 Measurement equipment for the evaporation experiment -

Nuclear Fuel Cycle
Quality and Standards for your converted material Hex Business at Springfields • Westinghouse will deliver on its promise of providing quality assurance for your company. • We pride ourselves on our engineering expertise and technical ability working to international standards including ISO 9001, 14001 and 18001. • Springfields has a long and successful history in the fuel cycle with over 40 years expertise in Hex conversion. Natural Mining Enrichment Fuel Fabrication Milling Nuclear Conversion Fuel Cycle Power Plant Reprocessing Electricity High Level Waste Storage Spent Fuel Storage www.westinghousenuclear.com Hex Business Rotary Kiln Plant Hex Plant Modern nuclear reactor designs such as Pressurised Water and Light Water Reactors To Atmosphere Uranium Trioxide UO – UF Conversion UF – UF Conversion UO 3 4 4 6 need nuclear fuel, made from Uranium Dioxide. 3 UO3 is transported to Kiln Plant in drums where it Uranium Hexafluoride is produced by the reaction UO To Atmosphere 3 is transferred onto a conveyor system. From here of UF with elemental gaseous fluorine in a Uranium Hexafluoride (UF6 ) is an essential intermediate product used in the Feed Hopper 4 Run Off Discharge the drums are delivered into the process via a fluidised bed reactor at 475°C. The fluorine manufacture of Uranium Dioxide fuels. Water UF6 mechanised tipping system. is produced by the electrolysis of anhydrous Condensers Hydration is the first stage in the treatment of hydrofluoric acid (AHF) in a potassium bi-fluoride Vac Back Air UO for the production of UF . electrolyte. 3 4 Secondary Meeting World Demands Advanced Technology Water Glycol Hydrator Heating & Cooling UO2 Transfer AHF Primary The Springfields Hex facilities are capable of Both plants demonstrate proven and state- To Scrubbers Hopper To Scrubbers H2 Transport Rotary Off-Gas Cylinder producing up to 5,500 tU of (UF6) annually, of-the-art technology. -

The Carbon Reduction of Uranium Oxide" (1964)
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Digital Repository @ Iowa State University Ames Laboratory Technical Reports Ames Laboratory 10-1964 The ac rbon reduction of uranium oxide H. A. Wilhelm Iowa State University Follow this and additional works at: http://lib.dr.iastate.edu/ameslab_isreports Part of the Ceramic Materials Commons, and the Metallurgy Commons Recommended Citation Wilhelm, H. A., "The carbon reduction of uranium oxide" (1964). Ames Laboratory Technical Reports. 86. http://lib.dr.iastate.edu/ameslab_isreports/86 This Report is brought to you for free and open access by the Ames Laboratory at Iowa State University Digital Repository. It has been accepted for inclusion in Ames Laboratory Technical Reports by an authorized administrator of Iowa State University Digital Repository. For more information, please contact [email protected]. The ac rbon reduction of uranium oxide Abstract The preparation of uranium metal directly from its oxides has been studied by a number of investigators. Various approaches have been pursued in these studies. Some attempts to produce the metal by electrolysis of the oxide in fused salt have been made; however, the reductions of the oxides by another metal and by carbon have attracted most attention. Although no entirely satisfactory method has yet been developed for preparation of uranium metal directly from oxide, the ready availability of high purity oxides makes such a process of interest. An investigation dealing with an approach to this problem is reported here. Disciplines Ceramic Materials | Metallurgy This report is available at Iowa State University Digital Repository: http://lib.dr.iastate.edu/ameslab_isreports/86 IS-1023 IOWA STATE UNIVERSITY THE CARBON REDUCTION OF URANIUM OXIDE by H. -
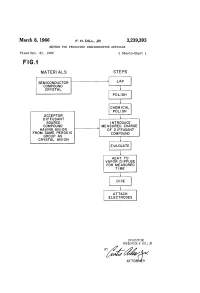
March 8, 1966 F. H. DIL, JR 3,239,393 METHOD for PRODUCING SEMICONDUCTOR ARTICLES Filed Dec
March 8, 1966 F. H. DIL, JR 3,239,393 METHOD FOR PRODUCING SEMICONDUCTOR ARTICLES Filed Dec. 31, 1962 2. Sheets-Sheet FG. MATER ALS STEPS SEMCONDUCTOR COMPOUND CRYSTAL POLISH CHEMICAL POLISH ACCEPTOR DFFUSANT SOURCE INTRODUCE COMPOUND MEASURED CHARGE HAVING AN ON OF DFFUSANT FROM SAME PERODC COMPOUND GROUP AS CRYSTAL ANION EVACUATE HEAT TO VAPOR DIFFUSE FOR MEASURED TIME ATTACH ELECTRODES INVENTOR. FREDERICK H. DLL JR ATTORNEY March 8, 1966 F., H., DL, JR 3,239,393 METHOD FOR PRODUCING SEMCONDUCTOR ARTICLES Filed Dec. 31, 962 2. Sheets-Sheet 2 Šes is series NNNNN r N NNNNNNNN 3,239,393 United States Patent Office Patented Mar. 8, 1966 2. to produce precisely the desired results. For instance, 3,239,393 when metallic zinc is used as the diffusant material for METHOD FOR PRODUCING SEMCONDUCTOR a gallium arsenide substrate, it is very difficult to obtain ARTICLES the pure zinc metal with no zinc oxide film upon the metal. Frederick H. Dii, Jr., Patnam Waley, N.Y., assigor to 5 Furthermore, the metal is so tough that it is difficult to International Business Machines Corporation, New divide a pure metal sample into smaller pieces in order York, N.Y., a corporation of New York to obtain exactly the correct quantity for the diffusion Filed Dec. 31, 1962, Ser. No. 248,679 process. The zinc oxide on the surface of the metallic Zinc 7 Claims. (C. 48-189) diffusant material is very undesirable for a number of This invention relates to an improved diffusion process IO reasons. The oxygen is not wanted in the diffusion Vapor, for the production of Semiconductor devices, and more and the zinc oxide tends to form a protective coating particularly to an improved vapor diffusion process in over the zinc which inhibits the formation of the desired which the introduction of unwanted impurities is very zinc metal vapor which is required for the diffusion proc effectively and simply avoided, and which possesses other CSS. -

Chemical Names and CAS Numbers Final
Chemical Abstract Chemical Formula Chemical Name Service (CAS) Number C3H8O 1‐propanol C4H7BrO2 2‐bromobutyric acid 80‐58‐0 GeH3COOH 2‐germaacetic acid C4H10 2‐methylpropane 75‐28‐5 C3H8O 2‐propanol 67‐63‐0 C6H10O3 4‐acetylbutyric acid 448671 C4H7BrO2 4‐bromobutyric acid 2623‐87‐2 CH3CHO acetaldehyde CH3CONH2 acetamide C8H9NO2 acetaminophen 103‐90‐2 − C2H3O2 acetate ion − CH3COO acetate ion C2H4O2 acetic acid 64‐19‐7 CH3COOH acetic acid (CH3)2CO acetone CH3COCl acetyl chloride C2H2 acetylene 74‐86‐2 HCCH acetylene C9H8O4 acetylsalicylic acid 50‐78‐2 H2C(CH)CN acrylonitrile C3H7NO2 Ala C3H7NO2 alanine 56‐41‐7 NaAlSi3O3 albite AlSb aluminium antimonide 25152‐52‐7 AlAs aluminium arsenide 22831‐42‐1 AlBO2 aluminium borate 61279‐70‐7 AlBO aluminium boron oxide 12041‐48‐4 AlBr3 aluminium bromide 7727‐15‐3 AlBr3•6H2O aluminium bromide hexahydrate 2149397 AlCl4Cs aluminium caesium tetrachloride 17992‐03‐9 AlCl3 aluminium chloride (anhydrous) 7446‐70‐0 AlCl3•6H2O aluminium chloride hexahydrate 7784‐13‐6 AlClO aluminium chloride oxide 13596‐11‐7 AlB2 aluminium diboride 12041‐50‐8 AlF2 aluminium difluoride 13569‐23‐8 AlF2O aluminium difluoride oxide 38344‐66‐0 AlB12 aluminium dodecaboride 12041‐54‐2 Al2F6 aluminium fluoride 17949‐86‐9 AlF3 aluminium fluoride 7784‐18‐1 Al(CHO2)3 aluminium formate 7360‐53‐4 1 of 75 Chemical Abstract Chemical Formula Chemical Name Service (CAS) Number Al(OH)3 aluminium hydroxide 21645‐51‐2 Al2I6 aluminium iodide 18898‐35‐6 AlI3 aluminium iodide 7784‐23‐8 AlBr aluminium monobromide 22359‐97‐3 AlCl aluminium monochloride