Models of Saturn's Protoplanetary Disk Forming In-Situ Its Regular Satellites
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

A Deeper Look at the Colors of the Saturnian Irregular Satellites Arxiv
A deeper look at the colors of the Saturnian irregular satellites Tommy Grav Harvard-Smithsonian Center for Astrophysics, MS51, 60 Garden St., Cambridge, MA02138 and Instiute for Astronomy, University of Hawaii, 2680 Woodlawn Dr., Honolulu, HI86822 [email protected] James Bauer Jet Propulsion Laboratory, California Institute of Technology 4800 Oak Grove Dr., MS183-501, Pasadena, CA91109 [email protected] September 13, 2018 arXiv:astro-ph/0611590v2 8 Mar 2007 Manuscript: 36 pages, with 11 figures and 5 tables. 1 Proposed running head: Colors of Saturnian irregular satellites Corresponding author: Tommy Grav MS51, 60 Garden St. Cambridge, MA02138 USA Phone: (617) 384-7689 Fax: (617) 495-7093 Email: [email protected] 2 Abstract We have performed broadband color photometry of the twelve brightest irregular satellites of Saturn with the goal of understanding their surface composition, as well as their physical relationship. We find that the satellites have a wide variety of different surface colors, from the negative spectral slopes of the two retrograde satellites S IX Phoebe (S0 = −2:5 ± 0:4) and S XXV Mundilfari (S0 = −5:0 ± 1:9) to the fairly red slope of S XXII Ijiraq (S0 = 19:5 ± 0:9). We further find that there exist a correlation between dynamical families and spectral slope, with the prograde clusters, the Gallic and Inuit, showing tight clustering in colors among most of their members. The retrograde objects are dynamically and physically more dispersed, but some internal structure is apparent. Keywords: Irregular satellites; Photometry, Satellites, Surfaces; Saturn, Satellites. 3 1 Introduction The satellites of Saturn can be divided into two distinct groups, the regular and irregular, based on their orbital characteristics. -

Cassini Observations of Saturn's Irregular Moons
EPSC Abstracts Vol. 12, EPSC2018-103-1, 2018 European Planetary Science Congress 2018 EEuropeaPn PlanetarSy Science CCongress c Author(s) 2018 Cassini Observations of Saturn's Irregular Moons Tilmann Denk (1) and Stefano Mottola (2) (1) Freie Universität Berlin, Germany ([email protected]), (2) DLR Berlin, Germany 1. Introduction two prograde irregulars are slower than ~13 h, while the periods of all but two retrogrades are faster than With the ISS-NAC camera of the Cassini spacecraft, ~13 h. The fastest period (Hati) is much slower than we obtained photometric lightcurves of 25 irregular the disruption rotation barrier for asteroids (~2.3 h), moons of Saturn. The goal was to derive basic phys- indicating that Saturn's irregulars may be rubble piles ical properties of these objects (like rotational periods, of rather low densities, possibly as low as of comets. shapes, pole-axis orientations, possible global color variations, ...) and to get hints on their formation and Table: Rotational periods of 25 Saturnian irregulars evolution. Our campaign marks the first utilization of an interplanetary probe for a systematic photometric Moon Approx. size Rotational period survey of irregular moons. name [km] [h] Hati 5 5.45 ± 0.04 The irregular moons are a class of objects that is very Mundilfari 7 6.74 ± 0.08 distinct from the inner moons of Saturn. Not only are Loge 5 6.9 ± 0.1 ? they more numerous (38 versus 24), but also occupy Skoll 5 7.26 ± 0.09 (?) a much larger volume within the Hill sphere of Suttungr 7 7.67 ± 0.02 Saturn. -

PDS4 Context List
Target Context List Name Type LID 136108 HAUMEA Planet urn:nasa:pds:context:target:planet.136108_haumea 136472 MAKEMAKE Planet urn:nasa:pds:context:target:planet.136472_makemake 1989N1 Satellite urn:nasa:pds:context:target:satellite.1989n1 1989N2 Satellite urn:nasa:pds:context:target:satellite.1989n2 ADRASTEA Satellite urn:nasa:pds:context:target:satellite.adrastea AEGAEON Satellite urn:nasa:pds:context:target:satellite.aegaeon AEGIR Satellite urn:nasa:pds:context:target:satellite.aegir ALBIORIX Satellite urn:nasa:pds:context:target:satellite.albiorix AMALTHEA Satellite urn:nasa:pds:context:target:satellite.amalthea ANTHE Satellite urn:nasa:pds:context:target:satellite.anthe APXSSITE Equipment urn:nasa:pds:context:target:equipment.apxssite ARIEL Satellite urn:nasa:pds:context:target:satellite.ariel ATLAS Satellite urn:nasa:pds:context:target:satellite.atlas BEBHIONN Satellite urn:nasa:pds:context:target:satellite.bebhionn BERGELMIR Satellite urn:nasa:pds:context:target:satellite.bergelmir BESTIA Satellite urn:nasa:pds:context:target:satellite.bestia BESTLA Satellite urn:nasa:pds:context:target:satellite.bestla BIAS Calibrator urn:nasa:pds:context:target:calibrator.bias BLACK SKY Calibration Field urn:nasa:pds:context:target:calibration_field.black_sky CAL Calibrator urn:nasa:pds:context:target:calibrator.cal CALIBRATION Calibrator urn:nasa:pds:context:target:calibrator.calibration CALIMG Calibrator urn:nasa:pds:context:target:calibrator.calimg CAL LAMPS Calibrator urn:nasa:pds:context:target:calibrator.cal_lamps CALLISTO Satellite urn:nasa:pds:context:target:satellite.callisto -

Perfect Little Planet Educator's Guide
Educator’s Guide Perfect Little Planet Educator’s Guide Table of Contents Vocabulary List 3 Activities for the Imagination 4 Word Search 5 Two Astronomy Games 7 A Toilet Paper Solar System Scale Model 11 The Scale of the Solar System 13 Solar System Models in Dough 15 Solar System Fact Sheet 17 2 “Perfect Little Planet” Vocabulary List Solar System Planet Asteroid Moon Comet Dwarf Planet Gas Giant "Rocky Midgets" (Terrestrial Planets) Sun Star Impact Orbit Planetary Rings Atmosphere Volcano Great Red Spot Olympus Mons Mariner Valley Acid Solar Prominence Solar Flare Ocean Earthquake Continent Plants and Animals Humans 3 Activities for the Imagination The objectives of these activities are: to learn about Earth and other planets, use language and art skills, en- courage use of libraries, and help develop creativity. The scientific accuracy of the creations may not be as im- portant as the learning, reasoning, and imagination used to construct each invention. Invent a Planet: Students may create (draw, paint, montage, build from household or classroom items, what- ever!) a planet. Does it have air? What color is its sky? Does it have ground? What is its ground made of? What is it like on this world? Invent an Alien: Students may create (draw, paint, montage, build from household items, etc.) an alien. To be fair to the alien, they should be sure to provide a way for the alien to get food (what is that food?), a way to breathe (if it needs to), ways to sense the environment, and perhaps a way to move around its planet. -

Request Riders Start (SCET) Start (Calenda Duration
Request Riders Start (SCET) Start (calenda Duration End Primary Secondary Comments (SPASS) Object Samp Line Phase Mag Post‐downlink comments (Tilmann Denk, FU Berlin) (pre‐ Notes : This spreadsheet somehow summarizes the Cassini observations of dic‐ For this sheet, information from the Project's SPASSes (SPacecraft Attitude ted) Almost all observations in this sheet were planned by myself (at DLR and Fr The SATELLORB requests (displayed in blue in this sheet) were planned by t Rider instruments (mainly UVIS and VIMS) can be taken from column B. No An occasionally updated version of this document plus lots of other stuff co https://tilmanndenk.de/outersaturnianmoons Cruise phase (Jupiter flyby) This is the document version of 15 Mar 2018. Sequence C023 2000‐310T05:25:00 069T21:35:00 2001‐014T03:00:00 VIMS_C23HI_HIM1X1001_PRIME I, U 2000‐353T20:00:00 2000‐12‐18 000T06:00:00 2000‐354T02:00:00 (Himalia) Himalia 789 237 70 disk‐res. Irregular moon of Jupiter. Object was resolved (~4x6 NAC pixels). Very redu Cruise phase (Saturn approach) Sequence S001, length = 35 ... 2004‐135T18:40:00 036T03:12:00 2004‐171T21:52:00 ISS_000PH_FULROTIN001_PRIME C, U, V 2004‐162T01:53:00 2004‐06‐10 000T11:44:00 2004‐162T13:37:00 CIRS_FP3 to Phoebe NEG_X to Sun Accomodate CIRS and U Phoebe 530 340 87 disk‐res. Day before targeted flyby. Phoebe is already visible as a disk. ISS_000PH_LOWRES0001_PRIME C, U 2004‐163T05:23:00 2004‐06‐11 000T00:16:00 2004‐163T05:39:00 ISS_NAC to Phoebe POS_Z to NEP S_N_ER_‐5a Phoebe 87 disk‐res. Targeted flyby inbound. -

Rotation Periods of Irregular Satellites of Saturn
EPSC Abstracts Vol. 6, EPSC-DPS2011-1452, 2011 EPSC-DPS Joint Meeting 2011 c Author(s) 2011 Rotation Periods of Irregular Satellites of Saturn T. Denk (1), S. Mottola (2), Th. Roatsch (2), H. Rosenberg (1), and G. Neukum (1) (1) FU Berlin, Germany ([email protected]), (2) DLR Berlin, Germany Abstract ~60x to ~240x closer to the objects than the Earth is, and long duration observations are possible because Rotation periods of six irregular moons of Saturn there is no 24-h day/night cycle at Cassini. Dis- have been measured as follows: Siarnaq ~06:40 h; advantages are the relatively small telescope mirror Ymir ~07:20 h; Albiorix 13:19±0:08 h; Bebhionn of the Cassini ISS camera (0.17 m), the smaller field- ~16 h; Paaliaq ~19 h; Kiviuq 21:49±0:13 h (Tab. 1). of-view of the ISS resulting in a significantly higher pointing accuracy requirement, and the inability of doing image quality checks and exposure parameter 1. Introduction adaptations during data acquisition. We observe irregular moons of Saturn with the Imaging Experiment (ISS) of the Cassini spacecraft 2. Results [1]. Motivation is the determination of basic properties of these objects like rotation periods, polar Measured rotation periods for seven satellites are axes orientations, object sizes and shapes, phase shown in Tab. 1. The values vary significantly: curves, colors, or the search for binaries. This might While Siarnaq, with a period of ~6 h 40 min., rotates allow a better understanding of the impact history in relatively fast, Kiviuq needs almost 22 h for one the saturnian system including the question about the day/night cycle. -

Irregular Satellites of the Giant Planets 411
Nicholson et al.: Irregular Satellites of the Giant Planets 411 Irregular Satellites of the Giant Planets Philip D. Nicholson Cornell University Matija Cuk University of British Columbia Scott S. Sheppard Carnegie Institution of Washington David Nesvorný Southwest Research Institute Torrence V. Johnson Jet Propulsion Laboratory The irregular satellites of the outer planets, whose population now numbers over 100, are likely to have been captured from heliocentric orbit during the early period of solar system history. They may thus constitute an intact sample of the planetesimals that accreted to form the cores of the jovian planets. Ranging in diameter from ~2 km to over 300 km, these bodies overlap the lower end of the presently known population of transneptunian objects (TNOs). Their size distributions, however, appear to be significantly shallower than that of TNOs of comparable size, suggesting either collisional evolution or a size-dependent capture probability. Several tight orbital groupings at Jupiter, supported by similarities in color, attest to a common origin followed by collisional disruption, akin to that of asteroid families. But with the limited data available to date, this does not appear to be the case at Uranus or Neptune, while the situa- tion at Saturn is unclear. Very limited spectral evidence suggests an origin of the jovian irregu- lars in the outer asteroid belt, but Saturn’s Phoebe and Neptune’s Nereid have surfaces domi- nated by water ice, suggesting an outer solar system origin. The short-term dynamics of many of the irregular satellites are dominated by large-amplitude coupled oscillations in eccentricity and inclination and offer several novel features, including secular resonances. -
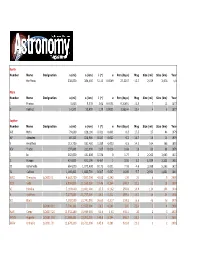
Moon-O-Meter
Earth Number Name Designation a (mi) a (km) i (°) e Per (days) Mag Size (mi) Size (km) Year the Moon 238,800 384,400 5.145 0.0549 27.3217 -12.7 2,159 3,476 n/a Mars Number Name Designation a (mi) a (km) i (°) e Per (days) Mag Size (mi) Size (km) Year I Phobos 5,825 9,378 1.08 0.0151 0.31891 11.3 7 11 1877 II Deimos 14,571 23,459 1.79 0.0005 1.26244 12.4 4 6 1877 Jupiter Number Name Designation a (mi) a (km) i (°) e Per (days) Mag Size (mi) Size (km) Year XVI Metis 79,600 128,100 0.021 0.001 0.3 17.5 27 44 1979 XV Adrastea 80,100 128,900 0.027 0.002 0.3 18.7 10 16 1979 V Amalthea 112,700 181,400 0.389 0.003 0.5 14.1 104 168 1892 XIV Thebe 137,800 221,900 1.07 0.018 0.68 16 61 98 1979 I Io 262,000 421,800 0.036 0 1.77 5 2,263 3,643 1610 II Europa 416,800 671,100 0.467 0 3.55 5.3 1,939 3,122 1610 III Ganymede 664,800 1,070,400 0.172 0.001 7.16 4.6 3,268 5,262 1610 IV Callisto 1,169,400 1,882,700 0.307 0.007 16.69 5.7 2,994 4,821 1610 XVIII Themisto S/2000 J1 4,662,700 7,507,000 43.08 0.242 130 21 6 9 2000 XIII Leda 6,934,800 11,165,000 27.46 0.164 240.9 20.2 11 18 1974 VI Himalia 7,118,600 11,461,000 27.5 0.162 250.6 14.8 114 184 1904 X Lysithea 7,277,600 11,717,000 28.3 0.112 259.2 18.2 24 38 1938 VII Elara 7,292,500 11,741,000 26.63 0.217 259.6 16.6 48 78 1905 S/2000 J11 7,798,100 12,555,000 28.3 0.248 287 22.4 2 4 2000 XLVI Carpo S/2003 J20 10,552,200 16,989,000 51.4 0.43 456.1 23 2 3 2003 XXXIV Euporie S/2001 J10 11,988,800 19,302,000 145.8 0.144 550.7 23.1 1 2 2001 XXXV Orthosie S/2001 J9 12,870,200 20,721,000 145.9 0.281 622.6 23.1 -

Cassini Observations of Saturn's Irregular Moons. T
50th Lunar and Planetary Science Conference 2019 (LPI Contrib. No. 2132) 2654.pdf CASSINI OBSERVATIONS OF SATURN'S IRREGULAR MOONS. T. Denk1 and S. Mottola2, 1Freie Univer- sität Berlin, Malteserstr. 74-100, 12249 Berlin, Germany ([email protected]), 2Deutsches Zentrum für Luft- und Raumfahrt (DLR), Rutherfordstr. 2, 12489 Berlin, Germany ([email protected]). Introduction: Saturn's outer or irregular moons Since Cassini was located inside the orbits of the represent a distinct class of objects in the Solar Sys- irregular moons, but the illumination source (the Sun) tem. They were discovered between 2000 and 2007 was far away (outside the orbits), the phase angles except for Phoebe which has been photographed since could take all values between 0° and 180° (see Table 1 1898. The distances between Saturn and the 38 known for ranges of actual observation phases). This unique objects vary between 7.6 Gm (126 RS; Kiviuq periap- advantage of Cassini would be given to any spacecraft sis) and 33.2 Gm (550 RS; Surtur apoapsis). The irreg- orbiting a giant planet while observing outer moons. ulars are found on orbits of large eccentricity and high The total number of ISS images targeting irregular inclination, both prograde and retrograde. moons is ~38,000, obtained during ~200 observations. Large moon Phoebe has a retrograde orbit and ac- Our Cassini campaign represents the first utilization of counts for more than 98% of the total mass of Saturn's an interplanetary spacecraft for a systematic photomet- irregulars. Of the remaining mass, ~92% belongs to ric survey of irregular moons in the Solar System. -

Sidereal Periods, Pole Solutions, and Shape Models of Saturn's Irregular Moons
EPSC Abstracts Vol. 13, EPSC-DPS2019-710-2, 2019 EPSC-DPS Joint Meeting 2019 c Author(s) 2019. CC Attribution 4.0 license. Sidereal Periods, Pole Solutions, and Shape Models of Saturn's Irregular Moons Tilmann Denk (1) and Stefano Mottola (2) (1) Freie Universität Berlin, Germany ([email protected]), (2) DLR Berlin, Germany During the Cassini mission, the irregular moons of produce intolerable additional noise. Furthermore, Saturn [1] have been targeted more than 200 times due to platform stability control deadbanding, for remote observations, marking the first exploration observed objects moved back and forth on the CCD of irregular moons through an interplanetary space- over a range of 10-20 pixels with typical periods of craft orbiting the common planet [2]. The moons tens of minutes. For this reason undercorrected pixels have been observed with the Narrow Angle Camera would also contain an additional quasi-periodic noise (NAC) of Cassini's ISS instrument which was a signal. Therefore, we decided to use science observ- spacecraft-fixed Ritchey-Chretien reflector telescope ations taken close in time to the actual observation to with a focal length of 2 m and an aperture of 0.19 m produce updated dark frames for each individual [3]. Since the irregulars were (except for Phoebe observation. during a targeted flyby) always more than 4∙106 km and mostly even more than 107 km away from the Color data calibration will be done in a similar way. spacecraft and thus too far away for disk-resolved In addition, making use of data from Cassini-ISS imaging, the goal was to obtain lightcurves through observations of solar-analog stars 16 Cygni B and disk-integrated photometry. -
Cassini Small Bodies Observations
Cassini Small Bodies Observations Ymir Atlas Tilmann Denk Freie Universität Berlin, Germany 10th Small Bodies Assessment Group Meeting (SBAG) Washington, DC – Thu 09 Jan 2014 2:20 p.m. EST (8:20 p.m. CET) T.D. gratefully acknowledges the support of this research by the Deutsches Zentrum für Luft- und Raumfahrt (DLR) in Bonn (Germany) (grant no.: 50 OH 1102). Cassini Orbiter Remote Sensing (ORS) • Imaging (ISS NAC, WAC) • Vis./near-IR spectrometer (VIMS) • IR spectrometer (CIRS) • UV spectrometer (UVIS) ORS FOVs: = 3.5° = 0.35° Denk -- Cassini Small Bodies Observations – page 2 Small Bodies or "Rocks" of Saturn "Alkyonides" 3 38 "Irregulars" "Ring rocks", 9 • Methone, Anthe, Pallene • Phoebe, Siarnaq, Albiorix, "Sheperds", Paaliaq, Ymir, Kiviuq, "Co-orbitals" Orbits between Mimas • Tarvos, Ijiraq, Erriapus, and Enceladus Skathi, Hyrrokkin, Suttungr, • Pan, Daphnis, Atlas Prometheus, Pandora Mundilfari, Thrymr, Narvi, • Discovered by Cassini etc. Janus, Epimetheus Bestla, Kari, Tarqeq, Aegaeon • Beyond 11 million km (> 180 R ) • Inside Mimas orbit; 4 "Lagrange Moons" S partly inside A ring or "Trojans" • 9 prograde, 29 retrograde • Cassini: disk-resolved • Telesto, Calypso • Discovered from Earth & spectra Helene, Polydeuces • Cassini: only disk-integrated • L4 & L5 moons of (except Phoebe) Tethys, Dione Denk -- Cassini Small Bodies Observations – page 3 "Ring rocks" Pan, Daphnis Denk -- Cassini Small Bodies Observations – page 4 "Ring rocks" Pan Daphnis Atlas 34 x 21 km 9 x 6 km 41 x 19 km Denk -- Cassini Small Bodies Observations – page -

Moon Cards Mercury
SOLAR SYSTEM MOON CARDS MERCURY Number of known Moons: 0 Moon names: N/A SOLAR SYSTEM MOON CARDS VENUS Number of known Moons: 0 Moon names: N/A SOLAR SYSTEM MOON CARDS EARTH Number of known Moons: 1 Moon names: Moon SOLAR SYSTEM MOON CARDS MARS Number of known Moons: 2 Moon names: Phobos, Deimos SOLAR SYSTEM MOON CARDS JUPITER Number of known Moons: 67 Moon names: Io, Europa, Ganymede, Callisto, Amalthea, Himalia, Elara, Pasiphae, Sinope, Lysithea, Carme, Ananke, Leda, Metis, Adrastea, Thebe, Callirrhoe, Themisto, Kalyke, Iocaste, Erinome, Harpalyke, Isonoe, Praxidike, Megaclite, Taygete, Chaldene, Autonoe, Thyone, Hermippe, Eurydome, Sponde, Pasithee, Euanthe, Kale, Orthosie, Euporie, Aitne, Hegemone, Mneme, Aoede, Thelxinoe, Arche, Kallichore, Helike, Carpo, Eukelade, Cyllene, Kore, Herse, plus others yet to receive names SOLAR SYSTEM MOON CARDS SATURN Number of known Moons: 62 Moon names: Titan, Rhea, Iapetus, Dione, Tethys, Enceladus, Mimas, Hyperion, Prometheus, Pandora, Phoebe, Janus, Epimetheus, Helene, Telesto, Calypso, Atlas, Pan, Ymir, Paaliaq, Siarnaq, Tarvos, Kiviuq, Ijiraq, Thrymr, Skathi, Mundilfari, Erriapus, Albiorix, Suttungr, Aegaeon, Aegir, Anthe, Bebhionn, Bergelmir, Bestla, Daphnis, Farbauti, Fenrir, Fornjot, Greip, Hati, Hyrrokin, Jarnsaxa, Kari, Loge, Methone, Narvi, Pallene, Polydeuces, Skoll, Surtur Tarqeq plus others yet to receive names SOLAR SYSTEM MOON CARDS URANUS Number of known Moons: 27 Moon names: Cordelia, Ophelia, Bianca, Cressida, Desdemona, Juliet, Portia, Rosalind, Mab, Belinda, Perdita, Puck, Cupid, Miranda, Francisco, Ariel, Umbriel, Titania, Oberon, Caliban, Sycorax, Margaret, Prospero, Setebos, Stephano, Trinculo, Ferdinand SOLAR SYSTEM MOON CARDS NEPTUNE Number of known Moons: 14 Moon names: Triton, Nereid, Naiad, Thalassa, Despina, Galatea, Larissa, Proteus, Laomedia, Psamanthe, Sao, Neso, Halimede, plus one other yet to receive a name.