DOCSLIB.ORG

Moon-O-Meter

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text

Load more

Earth Number Name Designation a (mi) a (km) i (°) e Per (days) Mag Size (mi) Size (km) Year the Moon 238,800 384,400 5.145 0.0549 27.3217 -12.7 2,159 3,476 n/a Mars Number Name Designation a (mi) a (km) i (°) e Per (days) Mag Size (mi) Size (km) Year I Phobos 5,825 9,378 1.08 0.0151 0.31891 11.3 7 11 1877 II Deimos 14,571 23,459 1.79 0.0005 1.26244 12.4 4 6 1877 Jupiter Number Name Designation a (mi) a (km) i (°) e Per (days) Mag Size (mi) Size (km) Year XVI Metis 79,600 128,100 0.021 0.001 0.3 17.5 27 44 1979 XV Adrastea 80,100 128,900 0.027 0.002 0.3 18.7 10 16 1979 V Amalthea 112,700 181,400 0.389 0.003 0.5 14.1 104 168 1892 XIV Thebe 137,800 221,900 1.07 0.018 0.68 16 61 98 1979 I Io 262,000 421,800 0.036 0 1.77 5 2,263 3,643 1610 II Europa 416,800 671,100 0.467 0 3.55 5.3 1,939 3,122 1610 III Ganymede 664,800 1,070,400 0.172 0.001 7.16 4.6 3,268 5,262 1610 IV Callisto 1,169,400 1,882,700 0.307 0.007 16.69 5.7 2,994 4,821 1610 XVIII Themisto S/2000 J1 4,662,700 7,507,000 43.08 0.242 130 21 6 9 2000 XIII Leda 6,934,800 11,165,000 27.46 0.164 240.9 20.2 11 18 1974 VI Himalia 7,118,600 11,461,000 27.5 0.162 250.6 14.8 114 184 1904 X Lysithea 7,277,600 11,717,000 28.3 0.112 259.2 18.2 24 38 1938 VII Elara 7,292,500 11,741,000 26.63 0.217 259.6 16.6 48 78 1905 S/2000 J11 7,798,100 12,555,000 28.3 0.248 287 22.4 2 4 2000 XLVI Carpo S/2003 J20 10,552,200 16,989,000 51.4 0.43 456.1 23 2 3 2003 XXXIV Euporie S/2001 J10 11,988,800 19,302,000 145.8 0.144 550.7 23.1 1 2 2001 XXXV Orthosie S/2001 J9 12,870,200 20,721,000 145.9 0.281 622.6 23.1 1 2 2001 XXXIII Euanthe S/2001 J7 12,918,600 20,799,000 148.9 0.232 620.6 22.8 2 3 2001 XXIX Thyone S/2001 J2 13,006,200 20,940,000 148.5 0.229 627.3 22.3 2 4 2001 XL Mneme S/2003 J21 13,086,300 21,069,000 148.6 0.227 620 23.3 1 2 2003 XXII Harpalyke S/2000 J5 13,108,700 21,105,000 148.6 0.226 623.3 22.2 2 4 2000 XXX Hermippe S/2001 J3 13,124,800 21,131,000 150.7 0.21 633.9 22.1 2 4 2001 XXVII Praxidike S/2000 J7 13,134,800 21,147,000 149 0.23 625.3 21.2 4 7 2000 XLII Thelxinoe S/2003 J22 13,144,100 21,162,000 151.4 0.221 628.1 23.5 1 2 2003 XXIV Iocaste S/2000 J3 13,210,600 21,269,000 149.4 0.216 631.5 21.8 3 5 2000 XII Ananke 13,214,900 21,276,000 148.9 0.244 610.5 18.9 17 28 1951 XLIII Arche S/2002 J1 14,242,900 22,931,000 165 0.259 723.9 22.8 2 3 2002 XXXVIII Pasithee S/2001 J6 14,345,300 23,096,000 165.1 0.267 719.5 23.2 1 2 2001 XXI Chaldene S/2000 J10 14,396,900 23,179,000 165.2 0.251 723.8 22.5 2 4 2000 XXXVII Kale S/2001 J8 14,420,500 23,217,000 165 0.26 729.5 23 1 2 2001 XXVI Isonoe S/2000 J6 14,420,500 23,217,000 165.2 0.246 725.5 22.5 2 4 2000 XXXI Aitne S/2001 J11 14,429,200 23,231,000 165.1 0.264 730.2 22.7 2 3 2001 XXV Erinome S/2000 J4 14,459,000 23,279,000 164.9 0.266 728.3 22.8 2 3 2000 XX Taygete S/2000 J9 14,509,300 23,360,000 165.2 0.252 732.2 21.9 3 5 2000 XI Carme 14,536,600 23,404,000 164.9 0.253 702.3 17.9 29 46 1938 XXIII Kalyke S/2000 J2 14,647,800 23,583,000 165.2 0.245 743 21.8 3 5 2000 XLVII Eukelade S/2003 J1 14,696,300 23,661,000 165.5 0.272 746.4 22.6 2 4 2003 XLIV Kallichore S/2003 J11 14,933,500 24,043,000 165.5 0.264 764.7 23.7 1 2 2003 XLV Helike S/2003 J6 13,206,800 21,263,000 154.8 0.156 634.8 22.6 2 4 2003 XXXII Eurydome S/2001 J4 14,201,900 22,865,000 150.3 0.276 717.3 22.7 2 3 2001 XXVIII Autonoe S/2001 J1 14,309,900 23,039,000 152.9 0.334 762.7 22 2 4 2001 XXXVI Sponde S/2001 J5 14,588,200 23,487,000 151 0.312 748.3 23 1 2 2001 VIII Pasiphae 14,673,300 23,624,000 151.4 0.409 708 16.9 36 58 1908 XIX Megaclite S/2000 J8 14,786,300 23,806,000 152.8 0.421 752.8 21.7 4 6 2000 IX Sinope 14,868,900 23,939,000 158.1 0.25 724.5 18.3 24 38 1914 XXXIX Hegemone S/2003 J8 14,873,900 23,947,000 155.2 0.328 739.6 22.8 2 3 2003 XLI Aoede S/2003 J7 14,895,000 23,981,000 158.3 0.432 761.5 22.5 2 4 2003 XVII Callirrhoe S/1999 J1 14,970,200 24,102,000 147.1 0.283 758.8 20.8 4 7 1999 XLVIII Cyllene S/2003 J13 15,123,600 24,349,000 149.3 0.319 737.8 23.2 1 2 2003 S/2003 J2 17,745,600 28,570,410 151.8 0.38 982.5 23.2 1 2 2003 S/2003 J3 11,391,200 18,339,885 143.7 0.241 504 23.4 1 2 2003 S/2003 J4 14,445,900 23,257,920 144.9 0.204 723.2 23 1 2 2003 S/2003 J5 14,959,100 24,084,180 165 0.21 759.7 22.4 2 4 2003 S/2003 J9 13,938,900 22,441,680 164.5 0.269 683 23.7 1 1 2003 S/2003 J10 15,061,900 24,249,600 164.1 0.214 767 23.6 1 2 2003 S/2003 J12 11,802,800 19,002,480 145.8 0.376 533.3 23.9 1 1 2003 S/2003 J14 15,500,000 25,000,000 140.9 0.222 807.8 23.6 1 2 2003 S/2003 J15 13,700,000 22,000,000 140.8 0.11 668.4 23.5 1 2 2003 S/2003 J16 13,000,000 21,000,000 148.6 0.27 595.4 23.3 1 2 2003 S/2003 J17 13,700,000 22,000,000 163.7 0.19 690.3 23.4 1 2 2003 S/2003 J18 12,900,000 20,700,000 146.5 0.119 606.3 23.4 1 2 2003 S/2003 J19 14,200,000 22,800,000 162.9 0.334 701.3 23.7 1 2 2003 S/2003 J23 14,941,300 24,055,500 149.2 0.309 759.7 23.6 1 2 2003 Saturn Number Name Designation a (mi) a (km) i (°) e Per (days) Mag Size (mi) Size (km) Year XVIII Pan S/1981 S13 83,000 133,600 0 0 0.575 19 16 25 1981 S/2005 S1 84,800 136,505 4 7 2005 XV Atlas S/1980 S28 85,500 137,700 0 0 0.602 18.5 20 32 1980 XVI Prometheus S/1980 S27 86,600 139,400 0 0.002 0.613 15.5 62 100 1980 XVII Pandora S/1980 S26 88,000 141,700 0 0.004 0.629 16 52 84 1980 XI Epimetheus S/1980 S3 94,000 151,400 0.335 0.021 0.69 15 74 119 1980 X Janus S/1980 S1 94,100 151,500 0.165 0.007 0.7 14 111 178 1980 I Mimas 115,300 185,600 1.566 0.021 0.94 12.5 247 397 1789 XXXII Methone S/2004 S1 120,500 194,000 0 0 1.01 2 3 2004 XXXIII Pallene S/2004 S2 131,100 211,000 0 0 1.14 2 4 2004 II Enceladus 147,900 238,100 0.01 0 1.37 11.5 310 499 1789 XIII Telesto S/1980 S13 183,000 294,700 1.158 0.001 1.89 18 15 24 1980 III Tethys 183,000 294,700 0.168 0 1.89 10 658 1,060 1684 XIV Calypso S/1980 S25 183,000 294,700 1.473 0.001 1.89 18.5 12 19 1980 IV Dione 234,400 377,400 0.002 0 2.74 10 694 1,118 1684 XII Helene S/1980 S6 234,400 377,400 0.212 0 2.74 18 20 32 1980 XXXIV Polydeuces S/2004 S5 234,400 377,400 0 0 2.74 2 4 2004 V Rhea 327,400 527,100 0.327 0.001 4.518 9 949 1,528 1672 VI Titan 758,900 1,221,900 1.634 0.029 15.95 8 3,199 5,150 1655 VII Hyperion 909,400 1,464,100 0.568 0.018 21.28 14 165 266 1848 VIII Iapetus 2,211,700 3,560,800 7.57 0.028 79.33 10.5 892 1,436 1671 XXIV Kiviuq S/2000 S5 7,059,000 11,365,000 46.16 0.334 449.2 22 10 16 2000 XXII Ijiraq S/2000 S6 7,106,000 11,440,000 46.74 0.322 451.5 22.6 7 12 2000 IX Phoebe 8,040,000 12,944,300 174.8 0.164 548.2 16 75 120 1898 XX Paaliaq S/2000 S2 9,440,000 15,199,000 45.13 0.364 686.9 21.3 14 22 2000 XXVII Skathi S/2000 S8 9,719,000 15,647,000 152.7 0.27 728.9 23.6 5 8 2000 XXVI Albiorix S/2000 S11 10,189,000 16,404,000 33.98 0.478 783.5 20.5 20 32 2000 XXVIII Erriapo S/2000 S10 10,942,000 17,616,000 34.45 0.474 871.9 23 6 10 2000 XXIX Siarnaq S/2000 S3 11,280,000 18,160,000 45.56 0.295 893.1 20.1 25 40 2000 XXI Tarvos S/2000 S4 11,334,000 18,247,000 33.51 0.536 925.6 22.1 9 15 2000 XXV Mundilfari S/2000 S9 11,620,000 18,709,000 167.5 0.208 951.4 23.8 4 7 2000 XXXI Narvi S/2003 S1 11,627,000 18,719,000 134.6 0.352 956.2 23.8 4 7 2003 XXIII Suttungr S/2000 S12 12,089,000 19,463,000 175.8 0.114 1,016.3 23.9 4 7 2000 XXX Thrymr S/2000 S7 12,660,000 20,382,000 175.8 0.47 1,086.9 23.9 4 7 2000 XIX Ymir S/2000 S1 14,345,000 23,096,000 173.1 0.333 1,312.4 21.7 11 18 2000 S/2004 S7 12,298,000 19,800,000 165.1 0.58 1,103 24.5 4 6 2004 S/2004 S8 13,790,000 22,200,000 168 0.213 1,355 24.6 4 6 2004 S/2004 S9 12,300,000 19,800,000 157.6 0.235 1,077 24.7 3 5 2004 S/2004 S10 12,020,000 19,350,000 167 0.241 1,026 24.4 4 6 2004 S/2004 S11 10,530,000 16,950,000 41 0.336 822 24.1 4 6 2004 S/2004 S12 12,200,000 19,650,000 164 0.401 1,048 24.8 3 5 2004 S/2004 S13 11,460,000 18,450,000 167.4 0.273 906 24.5 4 6 2004 S/2004 S14 12,390,000 19,950,000 162.7 0.292 1,081 24.4 4 6 2004 S/2004 S15 11,650,000 18,750,000 156.9 0.18 1,008 24.2 4 6 2004 S/2004 S16 13,790,000 22,200,000 163 0.135 1,271 25 2 4 2004 S/2004 S17 11,550,000 18,600,000 166.6 0.259 986 25.2 2 4 2004 S/2004 S18 12,200,000 19,650,000 147.4 0.795 1,052 23.8 4 7 2004 Uranus Number Name Designation a (mi) a (km) i (°) e Per (days) Mag Size (mi) Size (km) Year VI Cordelia S/1986 U7 30,900 49,800 0.085 0 0.335 23.1 25 40 1986 VII Ophelia S/1986 U8 33,400 53,800 0.104 0.01 0.376 22.8 26 42 1986 VIII Bianca S/1986 U9 36,800 59,200 0.193 0.001 0.435 22 32 51 1986 IX Cressida S/1986 U3 38,400 61,800 0.006 0 0.464 21.1 50 80 1986 X Desdemona S/1986 U6 38,900 62,700 0.113 0 0.474 21.5 40 64 1986 XI Juliet S/1986 U2 40,000 64,400 0.065 0.001 0.493 20.6 58 93 1986 XII Portia S/1986 U1 41,100 66,100 0.059 0 0.513 19.9 84 135 1986 XIII Rosalind S/1980 S6 43,400 69,900 0.279 0 0.558 21.3 45 72 1986 S/2003 U2 46,500 74,800 0 0 0 26 6 10 2003 XIV Belinda S/1986 U5 46,800 75,300 0.031 0 0.624 21 50 80 1986 S/1986 U10 47,500 76,420 0 0 0.638 24 12 20 1986 XV Puck S/1985 U1 53,400 86,000 0.319 0 0.762 19.2 101 162 1985 S/2003 U1 60,700 97,734 0 0 0 26 6 10 2003 V Miranda 80,700 129,900 4.338 0.001 1.41 15.3 293 471 1948 I Ariel 118,600 190,900 0.041 0.001 2.52 13.2 719 1,158 1851 II Umbriel 165,200 266,000 0.128 0.004 4.14 14 726 1,169 1851 III Titania 271,000 436,300 0.079 0.001 8.71 13 980 1,578 1787 IV Oberon 362,400 583,500 0.068 0.001 13.46 13.2 945 1,522 1787 S/2001 U3 2,656,000 4,276,000 145.2 0.146 266.6 25 14 22 2001 XVI Caliban S/1997 U1 4,491,000 7,231,000 140.9 0.159 579.7 22.4 45 72 1997 XX Stephano S/1999 U2 4,971,000 8,004,000 144.1 0.229 677.4 24.1 20 32 1999 XXI Trinculo S/2001 U1 5,282,000 8,504,000 167.1 0.22 759 25.4 11 18 2001 XVII Sycorax
Recommended publications
  • Arxiv:1912.09192V2 [Astro-Ph.EP] 24 Feb 2020

    Arxiv:1912.09192V2 [Astro-Ph.EP] 24 Feb 2020

    Draft version February 25, 2020 Typeset using LATEX preprint style in AASTeX62 Photometric analyses of Saturn's small moons: Aegaeon, Methone and Pallene are dark; Helene and Calypso are bright. M. M. Hedman,1 P. Helfenstein,2 R. O. Chancia,1, 3 P. Thomas,2 E. Roussos,4 C. Paranicas,5 and A. J. Verbiscer6 1Department of Physics, University of Idaho, Moscow, ID 83844 2Cornell Center for Astrophysics and Planetary Science, Cornell University, Ithaca NY 14853 3Center for Imaging Science, Rochester Institute of Technology, Rochester NY 14623 4Max Planck Institute for Solar System Research, G¨ottingen,Germany 37077 5APL, John Hopkins University, Laurel MD 20723 6Department of Astronomy, University of Virginia, Charlottesville, VA 22904 ABSTRACT We examine the surface brightnesses of Saturn's smaller satellites using a photometric model that explicitly accounts for their elongated shapes and thus facilitates compar- isons among different moons. Analyses of Cassini imaging data with this model reveals that the moons Aegaeon, Methone and Pallene are darker than one would expect given trends previously observed among the nearby mid-sized satellites. On the other hand, the trojan moons Calypso and Helene have substantially brighter surfaces than their co-orbital companions Tethys and Dione. These observations are inconsistent with the moons' surface brightnesses being entirely controlled by the local flux of E-ring par- ticles, and therefore strongly imply that other phenomena are affecting their surface properties. The darkness of Aegaeon, Methone and Pallene is correlated with the fluxes of high-energy protons, implying that high-energy radiation is responsible for darkening these small moons. Meanwhile, Prometheus and Pandora appear to be brightened by their interactions with nearby dusty F ring, implying that enhanced dust fluxes are most likely responsible for Calypso's and Helene's excess brightness.
  • A Deeper Look at the Colors of the Saturnian Irregular Satellites Arxiv

    A Deeper Look at the Colors of the Saturnian Irregular Satellites Arxiv

    A deeper look at the colors of the Saturnian irregular satellites Tommy Grav Harvard-Smithsonian Center for Astrophysics, MS51, 60 Garden St., Cambridge, MA02138 and Instiute for Astronomy, University of Hawaii, 2680 Woodlawn Dr., Honolulu, HI86822 [email protected] James Bauer Jet Propulsion Laboratory, California Institute of Technology 4800 Oak Grove Dr., MS183-501, Pasadena, CA91109 [email protected] September 13, 2018 arXiv:astro-ph/0611590v2 8 Mar 2007 Manuscript: 36 pages, with 11 figures and 5 tables. 1 Proposed running head: Colors of Saturnian irregular satellites Corresponding author: Tommy Grav MS51, 60 Garden St. Cambridge, MA02138 USA Phone: (617) 384-7689 Fax: (617) 495-7093 Email: [email protected] 2 Abstract We have performed broadband color photometry of the twelve brightest irregular satellites of Saturn with the goal of understanding their surface composition, as well as their physical relationship. We find that the satellites have a wide variety of different surface colors, from the negative spectral slopes of the two retrograde satellites S IX Phoebe (S0 = −2:5 ± 0:4) and S XXV Mundilfari (S0 = −5:0 ± 1:9) to the fairly red slope of S XXII Ijiraq (S0 = 19:5 ± 0:9). We further find that there exist a correlation between dynamical families and spectral slope, with the prograde clusters, the Gallic and Inuit, showing tight clustering in colors among most of their members. The retrograde objects are dynamically and physically more dispersed, but some internal structure is apparent. Keywords: Irregular satellites; Photometry, Satellites, Surfaces; Saturn, Satellites. 3 1 Introduction The satellites of Saturn can be divided into two distinct groups, the regular and irregular, based on their orbital characteristics.
  • Models of a Protoplanetary Disk Forming In-Situ the Galilean And

    Models of a Protoplanetary Disk Forming In-Situ the Galilean And

    Models of a protoplanetary disk forming in-situ the Galilean and smaller nearby satellites before Jupiter is formed Dimitris M. Christodoulou1, 2 and Demosthenes Kazanas3 1 Lowell Center for Space Science and Technology, University of Massachusetts Lowell, Lowell, MA, 01854, USA. 2 Dept. of Mathematical Sciences, Univ. of Massachusetts Lowell, Lowell, MA, 01854, USA. E-mail: [email protected] 3 NASA/GSFC, Laboratory for High-Energy Astrophysics, Code 663, Greenbelt, MD 20771, USA. E-mail: [email protected] March 5, 2019 ABSTRACT We fit an isothermal oscillatory density model of Jupiter’s protoplanetary disk to the present-day Galilean and other nearby satellites and we determine the radial scale length of the disk, the equation of state and the central density of the primordial gas, and the rotational state of the Jovian nebula. Although the radial density profile of Jupiter’s disk was similar to that of the solar nebula, its rotational support against self-gravity was very low, a property that also guaranteed its long-term stability against self-gravity induced instabilities for millions of years. Keywords. planets and satellites: dynamical evolution and stability—planets and satellites: formation—protoplanetary disks 1. Introduction 2. Intrinsic and Oscillatory Solutions of the Isothermal Lane-Emden Equation with Rotation In previous work (Christodoulou & Kazanas 2019a,b), we pre- sented and discussed an isothermal model of the solar nebula 2.1. Intrinsic Analytical Solutions capable of forming protoplanets long before the Sun was actu- The isothermal Lane-Emden equation (Lane 1869; Emden 1907) ally formed, very much as currently observed in high-resolution with rotation (Christodoulou & Kazanas 2019a) takes the form (∼1-5 AU) observations of protostellar disks by the ALMA tele- of a second-order nonlinear inhomogeneous equation, viz.
  • JUICE Red Book

    JUICE Red Book

    ESA/SRE(2014)1 September 2014 JUICE JUpiter ICy moons Explorer Exploring the emergence of habitable worlds around gas giants Definition Study Report European Space Agency 1 This page left intentionally blank 2 Mission Description Jupiter Icy Moons Explorer Key science goals The emergence of habitable worlds around gas giants Characterise Ganymede, Europa and Callisto as planetary objects and potential habitats Explore the Jupiter system as an archetype for gas giants Payload Ten instruments Laser Altimeter Radio Science Experiment Ice Penetrating Radar Visible-Infrared Hyperspectral Imaging Spectrometer Ultraviolet Imaging Spectrograph Imaging System Magnetometer Particle Package Submillimetre Wave Instrument Radio and Plasma Wave Instrument Overall mission profile 06/2022 - Launch by Ariane-5 ECA + EVEE Cruise 01/2030 - Jupiter orbit insertion Jupiter tour Transfer to Callisto (11 months) Europa phase: 2 Europa and 3 Callisto flybys (1 month) Jupiter High Latitude Phase: 9 Callisto flybys (9 months) Transfer to Ganymede (11 months) 09/2032 – Ganymede orbit insertion Ganymede tour Elliptical and high altitude circular phases (5 months) Low altitude (500 km) circular orbit (4 months) 06/2033 – End of nominal mission Spacecraft 3-axis stabilised Power: solar panels: ~900 W HGA: ~3 m, body fixed X and Ka bands Downlink ≥ 1.4 Gbit/day High Δv capability (2700 m/s) Radiation tolerance: 50 krad at equipment level Dry mass: ~1800 kg Ground TM stations ESTRAC network Key mission drivers Radiation tolerance and technology Power budget and solar arrays challenges Mass budget Responsibilities ESA: manufacturing, launch, operations of the spacecraft and data archiving PI Teams: science payload provision, operations, and data analysis 3 Foreword The JUICE (JUpiter ICy moon Explorer) mission, selected by ESA in May 2012 to be the first large mission within the Cosmic Vision Program 2015–2025, will provide the most comprehensive exploration to date of the Jovian system in all its complexity, with particular emphasis on Ganymede as a planetary body and potential habitat.
  • The Moons of Jupiter – Orbital Synchrony 3

    The Moons of Jupiter – Orbital Synchrony 3

    The Moons of Jupiter – Orbital Synchrony 3 The figure above shows the orbits of many of Jupiter's numerous satellites. Each of these ‘moons’ orbits Jupiter in a different number of days. The image to the right shows the appearance of one of Jupiter’s moons Callisto. The orbit periods of many of the moons have simple relationships between them. When Jupiter’s moon Ganymede orbits 1/2 way around Jupiter, Jupiter's moon Europa orbits Jupiter once. When Jupiter’s moon Leda orbits Jupiter once, Ganymede orbits Jupiter 34 times. When Jupiter's moon Leda orbits Jupiter five times, the more distant moon Thelxinoe orbits Jupiter twice. When Leda orbits Jupiter three times, the moon Kalyke orbits Jupiter once. Example: 1/2 x Ganymede = 1 x Europa, so in the time it takes Europa to go once around Jupiter, Ganymede goes only ½ way around in its orbit. Problem 1 - How many times does Ganymede orbit Jupiter in the time it takes Europa to orbit six times? Problem 2 – How many times does Leda orbit Jupiter in the time it takes Ganymede to orbit Jupiter 6 times? Problem 3 - How many orbits will Thelxinoe have to complete around Jupiter before Kalyke orbits exactly five times? Space Math http://spacemath.gsfc.nasa.gov Answer Key 3 Problem 1 - How many times does Ganymede orbit Jupiter in the time it takes Europa to orbit six times? Answer: The information says that Europa orbits once when Ganymede orbits 1/2 times, so 1 x Europa = 1/2 x Ganymede and so 2 x Europa = 1 x Ganymede.
  • The Orbits of Saturn's Small Satellites Derived From

    The Orbits of Saturn's Small Satellites Derived From

    The Astronomical Journal, 132:692–710, 2006 August A # 2006. The American Astronomical Society. All rights reserved. Printed in U.S.A. THE ORBITS OF SATURN’S SMALL SATELLITES DERIVED FROM COMBINED HISTORIC AND CASSINI IMAGING OBSERVATIONS J. N. Spitale CICLOPS, Space Science Institute, 4750 Walnut Street, Suite 205, Boulder, CO 80301; [email protected] R. A. Jacobson Jet Propulsion Laboratory, California Institute of Technology, 4800 Oak Grove Drive, Pasadena, CA 91109-8099 C. C. Porco CICLOPS, Space Science Institute, 4750 Walnut Street, Suite 205, Boulder, CO 80301 and W. M. Owen, Jr. Jet Propulsion Laboratory, California Institute of Technology, 4800 Oak Grove Drive, Pasadena, CA 91109-8099 Received 2006 February 28; accepted 2006 April 12 ABSTRACT We report on the orbits of the small, inner Saturnian satellites, either recovered or newly discovered in recent Cassini imaging observations. The orbits presented here reflect improvements over our previously published values in that the time base of Cassini observations has been extended, and numerical orbital integrations have been performed in those cases in which simple precessing elliptical, inclined orbit solutions were found to be inadequate. Using combined Cassini and Voyager observations, we obtain an eccentricity for Pan 7 times smaller than previously reported because of the predominance of higher quality Cassini data in the fit. The orbit of the small satellite (S/2005 S1 [Daphnis]) discovered by Cassini in the Keeler gap in the outer A ring appears to be circular and coplanar; no external perturbations are appar- ent. Refined orbits of Atlas, Prometheus, Pandora, Janus, and Epimetheus are based on Cassini , Voyager, Hubble Space Telescope, and Earth-based data and a numerical integration perturbed by all the massive satellites and each other.
  • Astrometric Positions for 18 Irregular Satellites of Giant Planets from 23

    Astrometric Positions for 18 Irregular Satellites of Giant Planets from 23

    Astronomy & Astrophysics manuscript no. Irregulares c ESO 2018 October 20, 2018 Astrometric positions for 18 irregular satellites of giant planets from 23 years of observations,⋆,⋆⋆,⋆⋆⋆,⋆⋆⋆⋆ A. R. Gomes-Júnior1, M. Assafin1,†, R. Vieira-Martins1, 2, 3,‡, J.-E. Arlot4, J. I. B. Camargo2, 3, F. Braga-Ribas2, 5,D.N. da Silva Neto6, A. H. Andrei1, 2,§, A. Dias-Oliveira2, B. E. Morgado1, G. Benedetti-Rossi2, Y. Duchemin4, 7, J. Desmars4, V. Lainey4, W. Thuillot4 1 Observatório do Valongo/UFRJ, Ladeira Pedro Antônio 43, CEP 20.080-090 Rio de Janeiro - RJ, Brazil e-mail: [email protected] 2 Observatório Nacional/MCT, R. General José Cristino 77, CEP 20921-400 Rio de Janeiro - RJ, Brazil e-mail: [email protected] 3 Laboratório Interinstitucional de e-Astronomia - LIneA, Rua Gal. José Cristino 77, Rio de Janeiro, RJ 20921-400, Brazil 4 Institut de mécanique céleste et de calcul des éphémérides - Observatoire de Paris, UMR 8028 du CNRS, 77 Av. Denfert-Rochereau, 75014 Paris, France e-mail: [email protected] 5 Federal University of Technology - Paraná (UTFPR / DAFIS), Rua Sete de Setembro, 3165, CEP 80230-901, Curitiba, PR, Brazil 6 Centro Universitário Estadual da Zona Oeste, Av. Manual Caldeira de Alvarenga 1203, CEP 23.070-200 Rio de Janeiro RJ, Brazil 7 ESIGELEC-IRSEEM, Technopôle du Madrillet, Avenue Galilée, 76801 Saint-Etienne du Rouvray, France Received: Abr 08, 2015; accepted: May 06, 2015 ABSTRACT Context. The irregular satellites of the giant planets are believed to have been captured during the evolution of the solar system. Knowing their physical parameters, such as size, density, and albedo is important for constraining where they came from and how they were captured.
  • Exep Science Plan Appendix (SPA) (This Document)

    Exep Science Plan Appendix (SPA) (This Document)

    ExEP Science Plan, Rev A JPL D: 1735632 Release Date: February 15, 2019 Page 1 of 61 Created By: David A. Breda Date Program TDEM System Engineer Exoplanet Exploration Program NASA/Jet Propulsion Laboratory California Institute of Technology Dr. Nick Siegler Date Program Chief Technologist Exoplanet Exploration Program NASA/Jet Propulsion Laboratory California Institute of Technology Concurred By: Dr. Gary Blackwood Date Program Manager Exoplanet Exploration Program NASA/Jet Propulsion Laboratory California Institute of Technology EXOPDr.LANET Douglas Hudgins E XPLORATION PROGRAMDate Program Scientist Exoplanet Exploration Program ScienceScience Plan Mission DirectorateAppendix NASA Headquarters Karl Stapelfeldt, Program Chief Scientist Eric Mamajek, Deputy Program Chief Scientist Exoplanet Exploration Program JPL CL#19-0790 JPL Document No: 1735632 ExEP Science Plan, Rev A JPL D: 1735632 Release Date: February 15, 2019 Page 2 of 61 Approved by: Dr. Gary Blackwood Date Program Manager, Exoplanet Exploration Program Office NASA/Jet Propulsion Laboratory Dr. Douglas Hudgins Date Program Scientist Exoplanet Exploration Program Science Mission Directorate NASA Headquarters Created by: Dr. Karl Stapelfeldt Chief Program Scientist Exoplanet Exploration Program Office NASA/Jet Propulsion Laboratory California Institute of Technology Dr. Eric Mamajek Deputy Program Chief Scientist Exoplanet Exploration Program Office NASA/Jet Propulsion Laboratory California Institute of Technology This research was carried out at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration. © 2018 California Institute of Technology. Government sponsorship acknowledged. Exoplanet Exploration Program JPL CL#19-0790 ExEP Science Plan, Rev A JPL D: 1735632 Release Date: February 15, 2019 Page 3 of 61 Table of Contents 1.
  • Cassini Observations of Saturn's Irregular Moons

    Cassini Observations of Saturn's Irregular Moons

    EPSC Abstracts Vol. 12, EPSC2018-103-1, 2018 European Planetary Science Congress 2018 EEuropeaPn PlanetarSy Science CCongress c Author(s) 2018 Cassini Observations of Saturn's Irregular Moons Tilmann Denk (1) and Stefano Mottola (2) (1) Freie Universität Berlin, Germany ([email protected]), (2) DLR Berlin, Germany 1. Introduction two prograde irregulars are slower than ~13 h, while the periods of all but two retrogrades are faster than With the ISS-NAC camera of the Cassini spacecraft, ~13 h. The fastest period (Hati) is much slower than we obtained photometric lightcurves of 25 irregular the disruption rotation barrier for asteroids (~2.3 h), moons of Saturn. The goal was to derive basic phys- indicating that Saturn's irregulars may be rubble piles ical properties of these objects (like rotational periods, of rather low densities, possibly as low as of comets. shapes, pole-axis orientations, possible global color variations, ...) and to get hints on their formation and Table: Rotational periods of 25 Saturnian irregulars evolution. Our campaign marks the first utilization of an interplanetary probe for a systematic photometric Moon Approx. size Rotational period survey of irregular moons. name [km] [h] Hati 5 5.45 ± 0.04 The irregular moons are a class of objects that is very Mundilfari 7 6.74 ± 0.08 distinct from the inner moons of Saturn. Not only are Loge 5 6.9 ± 0.1 ? they more numerous (38 versus 24), but also occupy Skoll 5 7.26 ± 0.09 (?) a much larger volume within the Hill sphere of Suttungr 7 7.67 ± 0.02 Saturn.
  • Hesiod Theogony.Pdf

    Hesiod Theogony.Pdf

    Hesiod (8th or 7th c. BC, composed in Greek) The Homeric epics, the Iliad and the Odyssey, are probably slightly earlier than Hesiod’s two surviving poems, the Works and Days and the Theogony. Yet in many ways Hesiod is the more important author for the study of Greek mythology. While Homer treats cer- tain aspects of the saga of the Trojan War, he makes no attempt at treating myth more generally. He often includes short digressions and tantalizes us with hints of a broader tra- dition, but much of this remains obscure. Hesiod, by contrast, sought in his Theogony to give a connected account of the creation of the universe. For the study of myth he is im- portant precisely because his is the oldest surviving attempt to treat systematically the mythical tradition from the first gods down to the great heroes. Also unlike the legendary Homer, Hesiod is for us an historical figure and a real per- sonality. His Works and Days contains a great deal of autobiographical information, in- cluding his birthplace (Ascra in Boiotia), where his father had come from (Cyme in Asia Minor), and the name of his brother (Perses), with whom he had a dispute that was the inspiration for composing the Works and Days. His exact date cannot be determined with precision, but there is general agreement that he lived in the 8th century or perhaps the early 7th century BC. His life, therefore, was approximately contemporaneous with the beginning of alphabetic writing in the Greek world. Although we do not know whether Hesiod himself employed this new invention in composing his poems, we can be certain that it was soon used to record and pass them on.
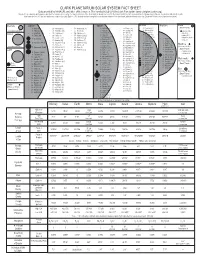
  • CLARK PLANETARIUM SOLAR SYSTEM FACT SHEET Data Provided by NASA/JPL and Other Official Sources

    CLARK PLANETARIUM SOLAR SYSTEM FACT SHEET Data Provided by NASA/JPL and Other Official Sources

    CLARK PLANETARIUM SOLAR SYSTEM FACT SHEET Data provided by NASA/JPL and other official sources. This handout ©July 2013 by Clark Planetarium (www.clarkplanetarium.org). May be freely copied by professional educators for classroom use only. The known satellites of the Solar System shown here next to their planets with their sizes (mean diameter in km) in parenthesis. The planets and satellites (with diameters above 1,000 km) are depicted in relative size (with Earth = 0.500 inches) and are arranged in order by their distance from the planet, with the closest at the top. Distances from moon to planet are not listed. Mercury Jupiter Saturn Uranus Neptune Pluto • 1- Metis (44) • 26- Hermippe (4) • 54- Hegemone (3) • 1- S/2009 S1 (1) • 33- Erriapo (10) • 1- Cordelia (40.2) (Dwarf Planet) (no natural satellites) • 2- Adrastea (16) • 27- Praxidike (6.8) • 55- Aoede (4) • 2- Pan (26) • 34- Siarnaq (40) • 2- Ophelia (42.8) • Charon (1186) • 3- Bianca (51.4) Venus • 3- Amalthea (168) • 28- Thelxinoe (2) • 56- Kallichore (2) • 3- Daphnis (7) • 35- Skoll (6) • Nix (60?) • 4- Thebe (98) • 29- Helike (4) • 57- S/2003 J 23 (2) • 4- Atlas (32) • 36- Tarvos (15) • 4- Cressida (79.6) • Hydra (50?) • 5- Desdemona (64) • 30- Iocaste (5.2) • 58- S/2003 J 5 (4) • 5- Prometheus (100.2) • 37- Tarqeq (7) • Kerberos (13-34?) • 5- Io (3,643.2) • 6- Pandora (83.8) • 38- Greip (6) • 6- Juliet (93.6) • 1- Naiad (58) • 31- Ananke (28) • 59- Callirrhoe (7) • Styx (??) • 7- Epimetheus (119) • 39- Hyrrokkin (8) • 7- Portia (135.2) • 2- Thalassa (80) • 6- Europa (3,121.6)
  • Cladistical Analysis of the Jovian Satellites. T. R. Holt1, A. J. Brown2 and D

    Cladistical Analysis of the Jovian Satellites. T. R. Holt1, A. J. Brown2 and D

    47th Lunar and Planetary Science Conference (2016) 2676.pdf Cladistical Analysis of the Jovian Satellites. T. R. Holt1, A. J. Brown2 and D. Nesvorny3, 1Center for Astrophysics and Supercomputing, Swinburne University of Technology, Melbourne, Victoria, Australia [email protected], 2SETI Institute, Mountain View, California, USA, 3Southwest Research Institute, Department of Space Studies, Boulder, CO. USA. Introduction: Surrounding Jupiter there are multi- Results: ple satellites, 67 known to-date. The most recent classi- fication system [1,2], based on orbital characteristics, uses the largest member of the group as the name and example. The closest group to Jupiter is the prograde Amalthea group, 4 small satellites embedded in a ring system. Moving outwards there are the famous Galilean moons, Io, Europa, Ganymede and Callisto, whose mass is similar to terrestrial planets. The final and largest group, is that of the outer Irregular satel- lites. Those irregulars that show a prograde orbit are closest to Jupiter and have previously been classified into three families [2], the Themisto, Carpo and Hi- malia groups. The remainder of the irregular satellites show a retrograde orbit, counter to Jupiter's rotation. Based on similarities in semi-major axis (a), inclination (i) and eccentricity (e) these satellites have been grouped into families [1,2]. In order outward from Jupiter they are: Ananke family (a 2.13x107 km ; i 148.9o; e 0.24); Carme family (a 2.34x107 km ; i 164.9o; e 0.25) and the Pasiphae family (a 2:36x107 km ; i 151.4o; e 0.41). There are some irregular satellites, recently discovered in 2003 [3], 2010 [4] and 2011[5], that have yet to be named or officially classified.