Genetic-Linkage Mapping of Complex Hereditary Disorders to a Whole-Genome Molecular-Interaction Network
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

RT² Profiler PCR Array (384-Well Format) Human Apoptosis 384HT
RT² Profiler PCR Array (384-Well Format) Human Apoptosis 384HT Cat. no. 330231 PAHS-3012ZE For pathway expression analysis Format For use with the following real-time cyclers RT² Profiler PCR Array, Applied Biosystems® models 7900HT (384-well block), Format E ViiA™ 7 (384-well block); Bio-Rad CFX384™ RT² Profiler PCR Array, Roche® LightCycler® 480 (384-well block) Format G Description The Human Apoptosis RT² Profiler PCR Array profiles the expression of 370 key genes involved in apoptosis, or programmed cell death. The array includes the TNF ligands and their receptors; members of the bcl-2 family, BIR (baculoviral IAP repeat) domain proteins, CARD domain (caspase recruitment domain) proteins, death domain proteins, TRAF (TNF receptor-associated factor) domain proteins and caspases. These 370 genes are also grouped by their functional contribution to apoptosis, either anti-apoptosis or induction of apoptosis. Using real-time PCR, you can easily and reliably analyze expression of a focused panel of genes related to apoptosis with this array. For further details, consult the RT² Profiler PCR Array Handbook. Sample & Assay Technologies Shipping and storage RT² Profiler PCR Arrays in formats E and G are shipped at ambient temperature, on dry ice, or blue ice packs depending on destination and accompanying products. For long term storage, keep plates at –20°C. Note: Ensure that you have the correct RT² Profiler PCR Array format for your real-time cycler (see table above). Note: Open the package and store the products appropriately immediately -

Genome-Wide Analysis of Host-Chromosome Binding Sites For
Lu et al. Virology Journal 2010, 7:262 http://www.virologyj.com/content/7/1/262 RESEARCH Open Access Genome-wide analysis of host-chromosome binding sites for Epstein-Barr Virus Nuclear Antigen 1 (EBNA1) Fang Lu1, Priyankara Wikramasinghe1, Julie Norseen1,2, Kevin Tsai1, Pu Wang1, Louise Showe1, Ramana V Davuluri1, Paul M Lieberman1* Abstract The Epstein-Barr Virus (EBV) Nuclear Antigen 1 (EBNA1) protein is required for the establishment of EBV latent infection in proliferating B-lymphocytes. EBNA1 is a multifunctional DNA-binding protein that stimulates DNA replication at the viral origin of plasmid replication (OriP), regulates transcription of viral and cellular genes, and tethers the viral episome to the cellular chromosome. EBNA1 also provides a survival function to B-lymphocytes, potentially through its ability to alter cellular gene expression. To better understand these various functions of EBNA1, we performed a genome-wide analysis of the viral and cellular DNA sites associated with EBNA1 protein in a latently infected Burkitt lymphoma B-cell line. Chromatin-immunoprecipitation (ChIP) combined with massively parallel deep-sequencing (ChIP-Seq) was used to identify cellular sites bound by EBNA1. Sites identified by ChIP- Seq were validated by conventional real-time PCR, and ChIP-Seq provided quantitative, high-resolution detection of the known EBNA1 binding sites on the EBV genome at OriP and Qp. We identified at least one cluster of unusually high-affinity EBNA1 binding sites on chromosome 11, between the divergent FAM55 D and FAM55B genes. A con- sensus for all cellular EBNA1 binding sites is distinct from those derived from the known viral binding sites, sug- gesting that some of these sites are indirectly bound by EBNA1. -

Molecular Profile of Tumor-Specific CD8+ T Cell Hypofunction in a Transplantable Murine Cancer Model
Downloaded from http://www.jimmunol.org/ by guest on September 25, 2021 T + is online at: average * The Journal of Immunology , 34 of which you can access for free at: 2016; 197:1477-1488; Prepublished online 1 July from submission to initial decision 4 weeks from acceptance to publication 2016; doi: 10.4049/jimmunol.1600589 http://www.jimmunol.org/content/197/4/1477 Molecular Profile of Tumor-Specific CD8 Cell Hypofunction in a Transplantable Murine Cancer Model Katherine A. Waugh, Sonia M. Leach, Brandon L. Moore, Tullia C. Bruno, Jonathan D. Buhrman and Jill E. Slansky J Immunol cites 95 articles Submit online. Every submission reviewed by practicing scientists ? is published twice each month by Receive free email-alerts when new articles cite this article. Sign up at: http://jimmunol.org/alerts http://jimmunol.org/subscription Submit copyright permission requests at: http://www.aai.org/About/Publications/JI/copyright.html http://www.jimmunol.org/content/suppl/2016/07/01/jimmunol.160058 9.DCSupplemental This article http://www.jimmunol.org/content/197/4/1477.full#ref-list-1 Information about subscribing to The JI No Triage! Fast Publication! Rapid Reviews! 30 days* Why • • • Material References Permissions Email Alerts Subscription Supplementary The Journal of Immunology The American Association of Immunologists, Inc., 1451 Rockville Pike, Suite 650, Rockville, MD 20852 Copyright © 2016 by The American Association of Immunologists, Inc. All rights reserved. Print ISSN: 0022-1767 Online ISSN: 1550-6606. This information is current as of September 25, 2021. The Journal of Immunology Molecular Profile of Tumor-Specific CD8+ T Cell Hypofunction in a Transplantable Murine Cancer Model Katherine A. -

Cytokine Nomenclature
RayBiotech, Inc. The protein array pioneer company Cytokine Nomenclature Cytokine Name Official Full Name Genbank Related Names Symbol 4-1BB TNFRSF Tumor necrosis factor NP_001552 CD137, ILA, 4-1BB ligand receptor 9 receptor superfamily .2. member 9 6Ckine CCL21 6-Cysteine Chemokine NM_002989 Small-inducible cytokine A21, Beta chemokine exodus-2, Secondary lymphoid-tissue chemokine, SLC, SCYA21 ACE ACE Angiotensin-converting NP_000780 CD143, DCP, DCP1 enzyme .1. NP_690043 .1. ACE-2 ACE2 Angiotensin-converting NP_068576 ACE-related carboxypeptidase, enzyme 2 .1 Angiotensin-converting enzyme homolog ACTH ACTH Adrenocorticotropic NP_000930 POMC, Pro-opiomelanocortin, hormone .1. Corticotropin-lipotropin, NPP, NP_001030 Melanotropin gamma, Gamma- 333.1 MSH, Potential peptide, Corticotropin, Melanotropin alpha, Alpha-MSH, Corticotropin-like intermediary peptide, CLIP, Lipotropin beta, Beta-LPH, Lipotropin gamma, Gamma-LPH, Melanotropin beta, Beta-MSH, Beta-endorphin, Met-enkephalin ACTHR ACTHR Adrenocorticotropic NP_000520 Melanocortin receptor 2, MC2-R hormone receptor .1 Activin A INHBA Activin A NM_002192 Activin beta-A chain, Erythroid differentiation protein, EDF, INHBA Activin B INHBB Activin B NM_002193 Inhibin beta B chain, Activin beta-B chain Activin C INHBC Activin C NM005538 Inhibin, beta C Activin RIA ACVR1 Activin receptor type-1 NM_001105 Activin receptor type I, ACTR-I, Serine/threonine-protein kinase receptor R1, SKR1, Activin receptor-like kinase 2, ALK-2, TGF-B superfamily receptor type I, TSR-I, ACVRLK2 Activin RIB ACVR1B -

Protein Interaction Network of Alternatively Spliced Isoforms from Brain Links Genetic Risk Factors for Autism
ARTICLE Received 24 Aug 2013 | Accepted 14 Mar 2014 | Published 11 Apr 2014 DOI: 10.1038/ncomms4650 OPEN Protein interaction network of alternatively spliced isoforms from brain links genetic risk factors for autism Roser Corominas1,*, Xinping Yang2,3,*, Guan Ning Lin1,*, Shuli Kang1,*, Yun Shen2,3, Lila Ghamsari2,3,w, Martin Broly2,3, Maria Rodriguez2,3, Stanley Tam2,3, Shelly A. Trigg2,3,w, Changyu Fan2,3, Song Yi2,3, Murat Tasan4, Irma Lemmens5, Xingyan Kuang6, Nan Zhao6, Dheeraj Malhotra7, Jacob J. Michaelson7,w, Vladimir Vacic8, Michael A. Calderwood2,3, Frederick P. Roth2,3,4, Jan Tavernier5, Steve Horvath9, Kourosh Salehi-Ashtiani2,3,w, Dmitry Korkin6, Jonathan Sebat7, David E. Hill2,3, Tong Hao2,3, Marc Vidal2,3 & Lilia M. Iakoucheva1 Increased risk for autism spectrum disorders (ASD) is attributed to hundreds of genetic loci. The convergence of ASD variants have been investigated using various approaches, including protein interactions extracted from the published literature. However, these datasets are frequently incomplete, carry biases and are limited to interactions of a single splicing isoform, which may not be expressed in the disease-relevant tissue. Here we introduce a new interactome mapping approach by experimentally identifying interactions between brain-expressed alternatively spliced variants of ASD risk factors. The Autism Spliceform Interaction Network reveals that almost half of the detected interactions and about 30% of the newly identified interacting partners represent contribution from splicing variants, emphasizing the importance of isoform networks. Isoform interactions greatly contribute to establishing direct physical connections between proteins from the de novo autism CNVs. Our findings demonstrate the critical role of spliceform networks for translating genetic knowledge into a better understanding of human diseases. -

By Submitted in Partial Satisfaction of the Requirements for Degree of in In
Developments of Two Imaging based Technologies for Cell Biology Researches by Xiaowei Yan DISSERTATION Submitted in partial satisfaction of the requirements for degree of DOCTOR OF PHILOSOPHY in Biochemistry and Molecular Biology in the GRADUATE DIVISION of the UNIVERSITY OF CALIFORNIA, SAN FRANCISCO Approved: ______________________________________________________________________________Ronald Vale Chair ______________________________________________________________________________Jonathan Weissman ______________________________________________________________________________Orion Weiner ______________________________________________________________________________ ______________________________________________________________________________ Committee Members Copyright 2021 By Xiaowei Yan ii DEDICATION Everything happens for the best. To my family, who supported me with all their love. iii ACKNOWLEDGEMENTS The greatest joy of my PhD has been joining UCSF, working and learning with such a fantastic group of scientists. I am extremely grateful for all the support and mentorship I received and would like to thank: My mentor, Ron Vale, who is such a great and generous person. Thank you for showing me that science is so much fun and thank you for always giving me the freedom in pursuing my interest. I am grateful for all the guidance from you and thank you for always supporting me whenever I needed. You are a person full of wisdom, and I have been learning so much from you and your attitude to science, science community and even life will continue inspire me. Thank you for being my mentor and thank you for being such a great mentor. Everyone else in Vale lab, past and present, for making our lab a sweet home. I would like to give my special thank to Marvin (Marvin Tanenbaum) and Nico (Nico Stuurman), two other mentors for me in the lab. I would like to thank them for helping me adapt to our lab, for all the valuable advice and for all the happiness during the time that we work together. -

Autism Multiplex Family with 16P11.2P12.2 Microduplication Syndrome in Monozygotic Twins and Distal 16P11.2 Deletion in Their Brother
European Journal of Human Genetics (2012) 20, 540–546 & 2012 Macmillan Publishers Limited All rights reserved 1018-4813/12 www.nature.com/ejhg ARTICLE Autism multiplex family with 16p11.2p12.2 microduplication syndrome in monozygotic twins and distal 16p11.2 deletion in their brother Anne-Claude Tabet1,2,3,4, Marion Pilorge2,3,4, Richard Delorme5,6,Fre´de´rique Amsellem5,6, Jean-Marc Pinard7, Marion Leboyer6,8,9, Alain Verloes10, Brigitte Benzacken1,11,12 and Catalina Betancur*,2,3,4 The pericentromeric region of chromosome 16p is rich in segmental duplications that predispose to rearrangements through non-allelic homologous recombination. Several recurrent copy number variations have been described recently in chromosome 16p. 16p11.2 rearrangements (29.5–30.1 Mb) are associated with autism, intellectual disability (ID) and other neurodevelopmental disorders. Another recognizable but less common microdeletion syndrome in 16p11.2p12.2 (21.4 to 28.5–30.1 Mb) has been described in six individuals with ID, whereas apparently reciprocal duplications, studied by standard cytogenetic and fluorescence in situ hybridization techniques, have been reported in three patients with autism spectrum disorders. Here, we report a multiplex family with three boys affected with autism, including two monozygotic twins carrying a de novo 16p11.2p12.2 duplication of 8.95 Mb (21.28–30.23 Mb) characterized by single-nucleotide polymorphism array, encompassing both the 16p11.2 and 16p11.2p12.2 regions. The twins exhibited autism, severe ID, and dysmorphic features, including a triangular face, deep-set eyes, large and prominent nasal bridge, and tall, slender build. The eldest brother presented with autism, mild ID, early-onset obesity and normal craniofacial features, and carried a smaller, overlapping 16p11.2 microdeletion of 847 kb (28.40–29.25 Mb), inherited from his apparently healthy father. -

Mouse Casp8ap2 Conditional Knockout Project (CRISPR/Cas9)
https://www.alphaknockout.com Mouse Casp8ap2 Conditional Knockout Project (CRISPR/Cas9) Objective: To create a Casp8ap2 conditional knockout Mouse model (C57BL/6J) by CRISPR/Cas-mediated genome engineering. Strategy summary: The Casp8ap2 gene (NCBI Reference Sequence: NM_011997 ; Ensembl: ENSMUSG00000028282 ) is located on Mouse chromosome 4. 11 exons are identified, with the ATG start codon in exon 2 and the TAG stop codon in exon 10 (Transcript: ENSMUST00000029950). Exon 4 will be selected as conditional knockout region (cKO region). Deletion of this region should result in the loss of function of the Mouse Casp8ap2 gene. To engineer the targeting vector, homologous arms and cKO region will be generated by PCR using BAC clone RP23-75H14 as template. Cas9, gRNA and targeting vector will be co-injected into fertilized eggs for cKO Mouse production. The pups will be genotyped by PCR followed by sequencing analysis. Note: Mice homozygous for disruption of this gene die before implantation. Exon 4 starts from about 2.12% of the coding region. The knockout of Exon 4 will result in frameshift of the gene. The size of intron 3 for 5'-loxP site insertion: 819 bp, and the size of intron 4 for 3'-loxP site insertion: 639 bp. The size of effective cKO region: ~601 bp. The cKO region does not have any other known gene. Page 1 of 7 https://www.alphaknockout.com Overview of the Targeting Strategy Wildtype allele gRNA region 5' gRNA region 3' 1 3 4 5 11 Targeting vector Targeted allele Constitutive KO allele (After Cre recombination) Legends Exon of mouse Casp8ap2 Homology arm cKO region loxP site Page 2 of 7 https://www.alphaknockout.com Overview of the Dot Plot Window size: 10 bp Forward Reverse Complement Sequence 12 Note: The sequence of homologous arms and cKO region is aligned with itself to determine if there are tandem repeats. -

A Computational Approach for Defining a Signature of Β-Cell Golgi Stress in Diabetes Mellitus
Page 1 of 781 Diabetes A Computational Approach for Defining a Signature of β-Cell Golgi Stress in Diabetes Mellitus Robert N. Bone1,6,7, Olufunmilola Oyebamiji2, Sayali Talware2, Sharmila Selvaraj2, Preethi Krishnan3,6, Farooq Syed1,6,7, Huanmei Wu2, Carmella Evans-Molina 1,3,4,5,6,7,8* Departments of 1Pediatrics, 3Medicine, 4Anatomy, Cell Biology & Physiology, 5Biochemistry & Molecular Biology, the 6Center for Diabetes & Metabolic Diseases, and the 7Herman B. Wells Center for Pediatric Research, Indiana University School of Medicine, Indianapolis, IN 46202; 2Department of BioHealth Informatics, Indiana University-Purdue University Indianapolis, Indianapolis, IN, 46202; 8Roudebush VA Medical Center, Indianapolis, IN 46202. *Corresponding Author(s): Carmella Evans-Molina, MD, PhD ([email protected]) Indiana University School of Medicine, 635 Barnhill Drive, MS 2031A, Indianapolis, IN 46202, Telephone: (317) 274-4145, Fax (317) 274-4107 Running Title: Golgi Stress Response in Diabetes Word Count: 4358 Number of Figures: 6 Keywords: Golgi apparatus stress, Islets, β cell, Type 1 diabetes, Type 2 diabetes 1 Diabetes Publish Ahead of Print, published online August 20, 2020 Diabetes Page 2 of 781 ABSTRACT The Golgi apparatus (GA) is an important site of insulin processing and granule maturation, but whether GA organelle dysfunction and GA stress are present in the diabetic β-cell has not been tested. We utilized an informatics-based approach to develop a transcriptional signature of β-cell GA stress using existing RNA sequencing and microarray datasets generated using human islets from donors with diabetes and islets where type 1(T1D) and type 2 diabetes (T2D) had been modeled ex vivo. To narrow our results to GA-specific genes, we applied a filter set of 1,030 genes accepted as GA associated. -

MMRN1 Antibody (Monoclonal) (M02) Mouse Monoclonal Antibody Raised Against a Partial Recombinant MMRN1
10320 Camino Santa Fe, Suite G San Diego, CA 92121 Tel: 858.875.1900 Fax: 858.622.0609 MMRN1 Antibody (monoclonal) (M02) Mouse monoclonal antibody raised against a partial recombinant MMRN1. Catalog # AT2883a Specification MMRN1 Antibody (monoclonal) (M02) - Product Information Application WB, E Primary Accession Q13201 Other Accession NM_007351 Reactivity Human Host mouse Clonality Monoclonal Isotype IgG2b Kappa Calculated MW 138110 MMRN1 Antibody (monoclonal) (M02) - Additional Information Antibody Reactive Against Recombinant Protein.Western Blot detection against Gene ID 22915 Immunogen (36.74 KDa) . Other Names Multimerin-1, EMILIN-4, Elastin microfibril interface located protein 4, Elastin microfibril interfacer 4, Endothelial cell multimerin, Platelet glycoprotein Ia*, 155 kDa platelet multimerin, p-155, p155, MMRN1, ECM, EMILIN4, GPIA*, MMRN Target/Specificity MMRN1 (NP_031377, 291 a.a. ~ 390 a.a) partial recombinant protein with GST tag. MW of the GST tag alone is 26 KDa. Detection limit for recombinant GST tagged MMRN1 is approximately 0.1ng/ml as a Dilution capture antibody. WB~~1:500~1000 Format MMRN1 Antibody (monoclonal) (M02) - Clear, colorless solution in phosphate Background buffered saline, pH 7.2 . Multimerin is a massive, soluble protein found Storage in platelets and in the endothelium of blood Store at -20°C or lower. Aliquot to avoid vessels. It is comprised of subunits linked by repeated freezing and thawing. interchain disulfide bonds to form large, variably sized homomultimers. Multimerin is a Precautions factor V/Va-binding protein and may function MMRN1 Antibody (monoclonal) (M02) is for as a carrier protein for platelet factor V. It may research use only and not for use in also have functions as an extracellular matrix diagnostic or therapeutic procedures. -

Transcriptional Control of Tissue-Resident Memory T Cell Generation
Transcriptional control of tissue-resident memory T cell generation Filip Cvetkovski Submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy in the Graduate School of Arts and Sciences COLUMBIA UNIVERSITY 2019 © 2019 Filip Cvetkovski All rights reserved ABSTRACT Transcriptional control of tissue-resident memory T cell generation Filip Cvetkovski Tissue-resident memory T cells (TRM) are a non-circulating subset of memory that are maintained at sites of pathogen entry and mediate optimal protection against reinfection. Lung TRM can be generated in response to respiratory infection or vaccination, however, the molecular pathways involved in CD4+TRM establishment have not been defined. Here, we performed transcriptional profiling of influenza-specific lung CD4+TRM following influenza infection to identify pathways implicated in CD4+TRM generation and homeostasis. Lung CD4+TRM displayed a unique transcriptional profile distinct from spleen memory, including up-regulation of a gene network induced by the transcription factor IRF4, a known regulator of effector T cell differentiation. In addition, the gene expression profile of lung CD4+TRM was enriched in gene sets previously described in tissue-resident regulatory T cells. Up-regulation of immunomodulatory molecules such as CTLA-4, PD-1, and ICOS, suggested a potential regulatory role for CD4+TRM in tissues. Using loss-of-function genetic experiments in mice, we demonstrate that IRF4 is required for the generation of lung-localized pathogen-specific effector CD4+T cells during acute influenza infection. Influenza-specific IRF4−/− T cells failed to fully express CD44, and maintained high levels of CD62L compared to wild type, suggesting a defect in complete differentiation into lung-tropic effector T cells. -
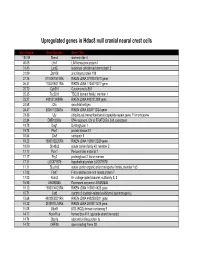
Supp Table 1.Pdf
Upregulated genes in Hdac8 null cranial neural crest cells fold change Gene Symbol Gene Title 134.39 Stmn4 stathmin-like 4 46.05 Lhx1 LIM homeobox protein 1 31.45 Lect2 leukocyte cell-derived chemotaxin 2 31.09 Zfp108 zinc finger protein 108 27.74 0710007G10Rik RIKEN cDNA 0710007G10 gene 26.31 1700019O17Rik RIKEN cDNA 1700019O17 gene 25.72 Cyb561 Cytochrome b-561 25.35 Tsc22d1 TSC22 domain family, member 1 25.27 4921513I08Rik RIKEN cDNA 4921513I08 gene 24.58 Ofa oncofetal antigen 24.47 B230112I24Rik RIKEN cDNA B230112I24 gene 23.86 Uty ubiquitously transcribed tetratricopeptide repeat gene, Y chromosome 22.84 D8Ertd268e DNA segment, Chr 8, ERATO Doi 268, expressed 19.78 Dag1 Dystroglycan 1 19.74 Pkn1 protein kinase N1 18.64 Cts8 cathepsin 8 18.23 1500012D20Rik RIKEN cDNA 1500012D20 gene 18.09 Slc43a2 solute carrier family 43, member 2 17.17 Pcm1 Pericentriolar material 1 17.17 Prg2 proteoglycan 2, bone marrow 17.11 LOC671579 hypothetical protein LOC671579 17.11 Slco1a5 solute carrier organic anion transporter family, member 1a5 17.02 Fbxl7 F-box and leucine-rich repeat protein 7 17.02 Kcns2 K+ voltage-gated channel, subfamily S, 2 16.93 AW493845 Expressed sequence AW493845 16.12 1600014K23Rik RIKEN cDNA 1600014K23 gene 15.71 Cst8 cystatin 8 (cystatin-related epididymal spermatogenic) 15.68 4922502D21Rik RIKEN cDNA 4922502D21 gene 15.32 2810011L19Rik RIKEN cDNA 2810011L19 gene 15.08 Btbd9 BTB (POZ) domain containing 9 14.77 Hoxa11os homeo box A11, opposite strand transcript 14.74 Obp1a odorant binding protein Ia 14.72 ORF28 open reading