DOCSLIB.ORG

Thermal Effects of High Energy and Ultrafast Lasers

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Thermal Effects of High Energy and Ultrafast Lasers THERMAL EFFECTS OF HIGH ENERGY AND ULTRAFAST LASERS A Thesis Presented to The Faculty of the Graduate School University of Missouri --------------------------------------------------------------------------------------------------------------------- In Partial Fulfillment of the Requirement for the Degree Doctor of Philosophy --------------------------------------------------------------------------------------------------------------------- By Nazia Afrin Thesis Supervisor: Dr. Yuwen Zhang December 2015 DECLARATION The undersigned, appointed by the dean of the Graduate Faculty, have examined the thesis entitled THERMAL EFFECTS OF HIGH ENERGY AND ULTRAFAST LASER Presented by NAZIA AFRIN A candidate for the degree of Doctor of Philosophy in Mechanical and Aerospace Engineering, and hereby certify that, in their opinion, it is worthy of acceptance. Professor Dr. Yuwen Zhang Professor Dr. Jinn-Kuen Chen Professor Dr. Gary Solbrekken Professor Dr. Matt Maschmann Professor Dr. Stephen Montgomery-Smith DEDICATION I dedicate this thesis to my parents, Shamsun Nahar Islam and late F.K.M. Aminul Islam, my husband Zobayer Khizir, my sister Dr. Aneesa Islam Keya for their endless love and support. ACKNOWLEDGEMENT I am highly grateful to my supervisor Professor Dr. Yuwen Zhang, Chairman of Department of Mechanical and Aerospace Engineering for his encouragement, support, patience and guidance throughout this research work also in daily life. This dissertation would not have been possible without guidance and help of him. I would like to thank the members of my thesis evaluation committee, Dr. J. K. Chen, Dr. Gary Solbrekken and Dr. Matt Maschmann and Dr. Stephen Montgomery-Smith for giving the time to provide valuable comments and criticism. Special thanks must be extended to Yijin Mao for his help.I would like to thank my all coworkers at my lab. It is really great time to work with them and I really enjoy their company in our lab. I would like to express my gratitude to my parents, Shamsun Nahar Islam and Late F. K. M Aminul Islam. My mother always gives me inspirations all the time about my study. Even though my father is not alive in this world, however, still I feel his contribution on my every success in my life. I also like to thanks my husband Zobayer Khizir for his support. Support for this work by the U.S. National Science Foundation under grant number CBET- 1066917 and CBET- 133611 are gratefully acknowledged. The authors would like to thank the Test Resource Management Center (TRMC) Test and Evaluation/Science & Technology (T&E/S&T) Program for their support. This work is funded by the T&E/S&T Program through the US Army Program Executive Office for Simulation, Training and Instrumentation’s contract number W900KK-08-C-0002. Support for this work by the Air Force Research Lab under grant number STTR FA9451-12 is gratefully acknowledged. ii TABLE OF CONTENTS ACKNOWLEDGEMENT ………………………………………………………………………ii LIST OF FIGURES………………………………………………………………………………vi LIST OF TABLE………………………………………………………...……………………… x NOMENCLATURE……………………………………………………..…………………..….. xi ABSTRACT…………………………………………………………………………………….xix CHAPTER 1: Introduction ……………………………………………………………...….….. 1 CHAPTER 2 Duel-Phase Lag behavior of a gas-saturated porous-medium heated by a short pulse laser 2.1 Introduction ………………………………………………………………..………………. 4 2.2 Physical model ……………………………………………………………………….……. 7 2.3 Laplace transform solution …………………………………………………….………….. 11 2.4 Results and discussion ……………………………………………………….……………. 13 2.5 Conclusion ………………………………………………………………………………… 23 CHAPTER 3 Inverse estimation of front surface temperature of a locally heated plate with temperature-dependent conductivity via Kirchhoff transformation 3.1 Introduction ……………………………………………………………………..…………. 25 3.2 Mathematical and approximation model ………………………………………..…………. 27 3.3 Laplace transform solution …………………………………………………………..…….. 32 3.4 Simulation results ………………………………………………………….……….……… 34 3.5 Conclusion ………………………………………………………………………….……… 44 CHAPTER 4 Multicomponent gas particle flow and heat/mass transfer induced by a localized laser irradiation on a Urethane-Coated stainless steel substrate 4.1 Introduction ………………………………………………………………………...………. 46 4.2 Physical model ……………………………………………………………………………....48 4.2.1 Continuous phase………..………………………………………………………………...48 iii 4.2.2 Chemical reaction ……………………………………………………………….………...52 4.2.3 Discretized phase …………………………………………………………….………….. 56 4.3 Results and discussion ……………………………………………….……………………. 57 4.4 Conclusion ………………………………………………………………………………… 79 CHAPTER 5 Effects of beam size and laser pulse duration on the laser drilling process 5.1 Introduction ………………………………………………………………………...………. 80 5.2 Analytical model …………………………………………………………………...………. 82 5.2.1 Fluid flow ……………………………………….………………………………..………. 83 5.2.2 Heat transfer………………….………………………………………………..…………..84 5.2.3 Optical consideration ….…………………………………………………..………..……. 85 5.3 Numerical simulation …………………………………………………………….………… 88 5.3.1 Velocity and pressure calculation ……………………….…………………….…………. 88 5.3.2 Temperature calculation (solving energy equation) ………………..………….…………89 5.4 Results and discussion ………………………………………………………..……….…… 90 5.4.1 Effects of beam diameter…………………………………………………………………..93 5.4.2 Effects of laser pulse……………………………………………………………………....97 5.5 Conclusion ………………………………………………………………...……………….102 CHPTER 6 Uncertainty analysis of melting and resolidification of gold film irradiated by nano- to-femtosecond lasers using Stochastic method 6.1 Introduction………………………………………………………………..……………….103 6.2 Physical model……………………………………………………………………………...106 6.3 Stochastic modeling of uncertainty…………………………………………………………110 6.4 Results and discussions……………………………………………………………………..112 6.5 Conclusion……………………………………………………..………………………….. 134 7. CONCLUSION ……………………………………………………………………………...135 iv REFERENCES ………………………………………………………………………….……. 138 VITA……………………………………………………………………………………………153 v LIST OF FIGURES Fig. 2-1 Physical model ………………………………………………………………………….8 Fig. 2-2 Powder temperature (Ts) at the heating surface and the adiabatic surface with J = 5 2 1.25×10 J/m , tp = 100 ns, dp = 15µm (τT = τq =3.9 ns): (a) t/tp < 1 and (b) t/tp > 1 …….….15 5 2 Fig. 2-3 Temperature distribution over the powder layer with J = 1.25×10 J/m , tp = 1 ns, dp = 15 µm (τT = τq = 3.9 ns)……………………………………………………………………………..16 Fig. 2-4 Phase lag times (τT and τq) effects on the powder layer temperature: (a) t/tp < 1 and (b) t/tp > 1………………………………………………………………………………………..…..19 Fig. 2-5 Effects of laser fluence (J) on the temperature of powder layer with tp = 10 ns and dp = 15 µm: (a) t/tp < 1 and (b) t/tp > 1…………………………………………………………….…20 5 2 Fig. 2-6 Effects of porosity (φ) on the temperature of powder layer with J = 1.25×10 J/m , tp = 1 ns, and dp = 15 µm: (a) t/tp < 1 and (b) t/tp > 1………………………………………………..22 5 Fig. 2-7 Effects of pulse width (tp) on the maximum temperature of powder layer (J=1.25×10 J/m2)…………………………………………………………………………………………...…23 Fig. 3-1 Relationship between T and for stainless steel with Tr 318 K………..….35 Fig. 3-2 Schematic diagram of meshing on the back surface ……………………………..….36 Fig. 3-3 Comparison of front surface temperature contours for SS 304: Exact (left), CGM (middle) and DCT/Laplace transformation solution (right)………………………………..….39 Fig. 3-4 Front surface temperature distributions along Y direction at different sensors location at time t=1.55s ………………………………………………………………………………….….40 Fig. 3-5 Comparison of front surface temperature between DCT/Laplace transformation and exact solution along Y direction at different sensors location at time t=1.55s ………………41 vi Fig. 3-6 Comparison of CGM and DCT/Laplace transformation solutions of front surface 19L 19L temperature vs time at three sensor locations (center ( Y Y , Z z ), two off centers ( 40 40 25L 19L 29L 19L Y Y , Z z and (Y Y , Z z )) …………………………………..……….…42 40 40 40 40 Fig. 3-7 Comparison of the RMS values at different time steps for DCT/Laplace (reference temperature (Tr) as all average values of back surface temperatures and average of maximum and minimum front surface temperatures) and CGM method ………………………………….…..44 Figure 4-1 Node moving mechanism ……………………………………………………….….55 Figure 4-2 Illustration of mesh arrangement ………………………………………………….58 Figure 4-3 Maxmum temperatures in the paint vs three different mesh configurations…….…64 Figure 4 Temperature distribution across the middle cross section area of the gaseous domain at the end of simulation …………………………………………………………....66 Figure 4-5 Time history of temperatures at the center of laser heating spot for the six laser powers …………………………………………………………………………..….66 Figure 4-6 Density distributions across the middle cross section area of the gaseous domain at the end of simulation …………………………………………………………..…...68 Figure 4-7 Density variations at the center of the laser irradiation spot with time ……..……69 Figure 4-8 Velocity distributions across the middle cross section area of the gaseous domain at the end of simulation ……………………………………………………………….70 Figure 4-9 State of parcel flow and gaseous phase at different times …………………..……72 Figure 4-10 Time histories of the mass concentration of O2, H2O, CO2, NO2 at the center of laser heating spot …………………………………………………………..…………......75 Figure 4-11 Time histories of paint thickness removal for the six laser powers ……….…….76 Figure 4-12 Parcel and gaseous flow at the end of the simulation ………………………..……77 Figure 4-13 Comparison of paint removal between simulation and experiment ………..…...78 vii Figure 5-1 Schematic diagram of laser drilling process……………………………………......83
Load more

Recommended publications
  • Glossary Glossary
    Glossary Glossary Albedo A measure of an object’s reflectivity. A pure white reflecting surface has an albedo of 1.0 (100%). A pitch-black, nonreflecting surface has an albedo of 0.0. The Moon is a fairly dark object with a combined albedo of 0.07 (reflecting 7% of the sunlight that falls upon it). The albedo range of the lunar maria is between 0.05 and 0.08. The brighter highlands have an albedo range from 0.09 to 0.15. Anorthosite Rocks rich in the mineral feldspar, making up much of the Moon’s bright highland regions. Aperture The diameter of a telescope’s objective lens or primary mirror. Apogee The point in the Moon’s orbit where it is furthest from the Earth. At apogee, the Moon can reach a maximum distance of 406,700 km from the Earth. Apollo The manned lunar program of the United States. Between July 1969 and December 1972, six Apollo missions landed on the Moon, allowing a total of 12 astronauts to explore its surface. Asteroid A minor planet. A large solid body of rock in orbit around the Sun. Banded crater A crater that displays dusky linear tracts on its inner walls and/or floor. 250 Basalt A dark, fine-grained volcanic rock, low in silicon, with a low viscosity. Basaltic material fills many of the Moon’s major basins, especially on the near side. Glossary Basin A very large circular impact structure (usually comprising multiple concentric rings) that usually displays some degree of flooding with lava. The largest and most conspicuous lava- flooded basins on the Moon are found on the near side, and most are filled to their outer edges with mare basalts.
    [Show full text]
  • Feature of the Month – January 2016 Galilaei
    A PUBLICATION OF THE LUNAR SECTION OF THE A.L.P.O. EDITED BY: Wayne Bailey [email protected] 17 Autumn Lane, Sewell, NJ 08080 RECENT BACK ISSUES: http://moon.scopesandscapes.com/tlo_back.html FEATURE OF THE MONTH – JANUARY 2016 GALILAEI Sketch and text by Robert H. Hays, Jr. - Worth, Illinois, USA October 26, 2015 03:32-03:58 UT, 15 cm refl, 170x, seeing 8-9/10 I sketched this crater and vicinity on the evening of Oct. 25/26, 2015 after the moon hid ZC 109. This was about 32 hours before full. Galilaei is a modest but very crisp crater in far western Oceanus Procellarum. It appears very symmetrical, but there is a faint strip of shadow protruding from its southern end. Galilaei A is the very similar but smaller crater north of Galilaei. The bright spot to the south is labeled Galilaei D on the Lunar Quadrant map. A tiny bit of shadow was glimpsed in this spot indicating a craterlet. Two more moderately bright spots are east of Galilaei. The western one of this pair showed a bit of shadow, much like Galilaei D, but the other one did not. Galilaei B is the shadow-filled crater to the west. This shadowing gave this crater a ring shape. This ring was thicker on its west side. Galilaei H is the small pit just west of B. A wide, low ridge extends to the southwest from Galilaei B, and a crisper peak is south of H. Galilaei B must be more recent than its attendant ridge since the crater's exterior shadow falls upon the ridge.
    [Show full text]
  • Toxicology in Antiquity
    TOXICOLOGY IN ANTIQUITY Other published books in the History of Toxicology and Environmental Health series Wexler, History of Toxicology and Environmental Health: Toxicology in Antiquity, Volume I, May 2014, 978-0-12-800045-8 Wexler, History of Toxicology and Environmental Health: Toxicology in Antiquity, Volume II, September 2014, 978-0-12-801506-3 Wexler, Toxicology in the Middle Ages and Renaissance, March 2017, 978-0-12-809554-6 Bobst, History of Risk Assessment in Toxicology, October 2017, 978-0-12-809532-4 Balls, et al., The History of Alternative Test Methods in Toxicology, October 2018, 978-0-12-813697-3 TOXICOLOGY IN ANTIQUITY SECOND EDITION Edited by PHILIP WEXLER Retired, National Library of Medicine’s (NLM) Toxicology and Environmental Health Information Program, Bethesda, MD, USA Academic Press is an imprint of Elsevier 125 London Wall, London EC2Y 5AS, United Kingdom 525 B Street, Suite 1650, San Diego, CA 92101, United States 50 Hampshire Street, 5th Floor, Cambridge, MA 02139, United States The Boulevard, Langford Lane, Kidlington, Oxford OX5 1GB, United Kingdom Copyright r 2019 Elsevier Inc. All rights reserved. No part of this publication may be reproduced or transmitted in any form or by any means, electronic or mechanical, including photocopying, recording, or any information storage and retrieval system, without permission in writing from the publisher. Details on how to seek permission, further information about the Publisher’s permissions policies and our arrangements with organizations such as the Copyright Clearance Center and the Copyright Licensing Agency, can be found at our website: www.elsevier.com/permissions. This book and the individual contributions contained in it are protected under copyright by the Publisher (other than as may be noted herein).
    [Show full text]
  • Glossary of Lunar Terminology
    Glossary of Lunar Terminology albedo A measure of the reflectivity of the Moon's gabbro A coarse crystalline rock, often found in the visible surface. The Moon's albedo averages 0.07, which lunar highlands, containing plagioclase and pyroxene. means that its surface reflects, on average, 7% of the Anorthositic gabbros contain 65-78% calcium feldspar. light falling on it. gardening The process by which the Moon's surface is anorthosite A coarse-grained rock, largely composed of mixed with deeper layers, mainly as a result of meteor­ calcium feldspar, common on the Moon. itic bombardment. basalt A type of fine-grained volcanic rock containing ghost crater (ruined crater) The faint outline that remains the minerals pyroxene and plagioclase (calcium of a lunar crater that has been largely erased by some feldspar). Mare basalts are rich in iron and titanium, later action, usually lava flooding. while highland basalts are high in aluminum. glacis A gently sloping bank; an old term for the outer breccia A rock composed of a matrix oflarger, angular slope of a crater's walls. stony fragments and a finer, binding component. graben A sunken area between faults. caldera A type of volcanic crater formed primarily by a highlands The Moon's lighter-colored regions, which sinking of its floor rather than by the ejection of lava. are higher than their surroundings and thus not central peak A mountainous landform at or near the covered by dark lavas. Most highland features are the center of certain lunar craters, possibly formed by an rims or central peaks of impact sites.
    [Show full text]
  • What's Hot on the Moon Tonight?: the Ultimate Guide to Lunar Observing
    What’s Hot on the Moon Tonight: The Ultimate Guide to Lunar Observing Copyright © 2015 Andrew Planck All rights reserved. No part of this book may be reproduced in any written, electronic, recording, or photocopying without written permission of the publisher or author. The exception would be in the case of brief quotations embodied in the critical articles or reviews and pages where permission is specifically granted by the publisher or author. Although every precaution has been taken to verify the accuracy of the information contained herein, the publisher and author assume no responsibility for any errors or omissions. No liability is assumed for damages that may result from the use of information contained within. Books may be purchased by contacting the publisher or author through the website below: AndrewPlanck.com Cover and Interior Design: Nick Zelinger (NZ Graphics) Publisher: MoonScape Publishing, LLC Editor: John Maling (Editing By John) Manuscript Consultant: Judith Briles (The Book Shepherd) ISBN: 978-0-9908769-0-8 Library of Congress Catalog Number: 2014918951 1) Science 2) Astronomy 3) Moon Dedicated to my wife, Susan and to my two daughters, Sarah and Stefanie Contents Foreword Acknowledgments How to Use this Guide Map of Major Seas Nightly Guide to Lunar Features DAYS 1 & 2 (T=79°-68° E) DAY 3 (T=59° E) Day 4 (T=45° E) Day 5 (T=24° E.) Day 6 (T=10° E) Day 7 (T=0°) Day 8 (T=12° W) Day 9 (T=21° W) Day 10 (T= 28° W) Day 11 (T=39° W) Day 12 (T=54° W) Day 13 (T=67° W) Day 14 (T=81° W) Day 15 and beyond Day 16 (T=72°) Day 17 (T=60°) FINAL THOUGHTS GLOSSARY Appendix A: Historical Notes Appendix B: Pronunciation Guide About the Author Foreword Andrew Planck first came to my attention when he submitted to Lunar Photo of the Day an image of the lunar crater Pitatus and a photo of a pie he had made.
    [Show full text]
  • Lunar Club Observations
    Guys & Gals, Here, belatedly, is my Christmas present to you. I couldn’t buy each of you a lunar map, so I did the next best thing. Below this letter you’ll find a guide for observing each of the 100 lunar features on the A. L.’s Lunar Club observing list. My guide tells you what the features are, where they are located, what instrument (naked eyes, binoculars or telescope) will give you the best view of them and what you can expect to see when you find them. It may or may not look like it, but this project involved a massive amount of work. In preparing it, I relied heavily on three resources: *The lunar map I used to determine which quadrant of the Moon each feature resides in is the laminated Sky & Telescope Lunar Map – specifically, the one that shows the Moon as we see it naked-eye or in binoculars. (S&T also sells one with the features reversed to match the view in a refracting telescope for the same price.); and *The text consists of information from (a) my own observing notes and (b) material in Ernest Cherrington’s Exploring the Moon Through Binoculars and Small Telescopes. Both the map and Cherrington’s book were door prizes at our Dec. Christmas party. My goal, of course, is to get you interested in learning more about our nearest neighbor in space. The Moon is a fascinating and lovely place, and one that all too often is overlooked by amateur astronomers. But of all the objects in the night sky, the Moon is the most accessible and easiest to observe.
    [Show full text]
  • Thumbnail Index
    Thumbnail Index The following five pages depict each plate in the book and provide the following information about it: • Longitude and latitude of the main feature shown. • Sun’s angle (SE), ranging from 1°, with grazing illumination and long shadows, up to 72° for nearly full Moon conditions with the Sun almost overhead. • The elevation or height (H) in kilometers of the spacecraft above the surface when the image was acquired, from 21 to 116 km. • The time of acquisition in this sequence: year, month, day, hour, and minute in Universal Time. 1. Gauss 2. Cleomedes 3. Yerkes 4. Proclus 5. Mare Marginis 79°E, 36°N SE=30° H=65km 2009.05.29. 05:15 56°Ｅ, 24°N SE=28° H=100km 2008.12.03. 09:02 52°Ｅ, 15°N SE=34° Ｈ=72km 2009.05.31. 06:07 48°Ｅ, 17°N SE=59° Ｈ=45km 2009.05.04. 06:40 87°Ｅ, 14°N SE=7° Ｈ=60km 2009.01.10. 22:29 6. Mare Smythii 7. Taruntius 8. Mare Fecunditatis 9. Langrenus 10. Petavius 86°Ｅ, 3°S SE=19° Ｈ=58km 2009.01.11. 00:28 47°Ｅ, 6°N SE=33° Ｈ=72km 2009.05.31. 15:27 50°Ｅ, 7°S SE=10° Ｈ=64km 2009.01.13. 19:40 60°Ｅ, 11°S SE=24° Ｈ=95km 2008.06.08. 08:10 61°Ｅ, 23°S SE=9° Ｈ=65km 2009.01.12. 22:42 11.Humboldt 12. Furnerius 13. Stevinus 14. Rheita Valley 15. Kaguya impact point 80°Ｅ, 27°S SE=42° Ｈ=105km 2008.05.10.
    [Show full text]
  • Greek Tragedy and the Epic Cycle: Narrative Tradition, Texts, Fragments
    GREEK TRAGEDY AND THE EPIC CYCLE: NARRATIVE TRADITION, TEXTS, FRAGMENTS By Daniel Dooley A dissertation submitted to Johns Hopkins University in conformity with the requirements for the degree of Doctor of Philosophy Baltimore, Maryland October 2017 © Daniel Dooley All Rights Reserved Abstract This dissertation analyzes the pervasive influence of the Epic Cycle, a set of Greek poems that sought collectively to narrate all the major events of the Trojan War, upon Greek tragedy, primarily those tragedies that were produced in the fifth century B.C. This influence is most clearly discernible in the high proportion of tragedies by Aeschylus, Sophocles, and Euripides that tell stories relating to the Trojan War and do so in ways that reveal the tragedians’ engagement with non-Homeric epic. An introduction lays out the sources, argues that the earlier literary tradition in the form of specific texts played a major role in shaping the compositions of the tragedians, and distinguishes the nature of the relationship between tragedy and the Epic Cycle from the ways in which tragedy made use of the Homeric epics. There follow three chapters each dedicated to a different poem of the Trojan Cycle: the Cypria, which communicated to Euripides and others the cosmic origins of the war and offered the greatest variety of episodes; the Little Iliad, which highlighted Odysseus’ career as a military strategist and found special favor with Sophocles; and the Telegony, which completed the Cycle by describing the peculiar circumstances of Odysseus’ death, attributed to an even more bizarre cause in preserved verses by Aeschylus. These case studies are taken to be representative of Greek tragedy’s reception of the Epic Cycle as a whole; while the other Trojan epics (the Aethiopis, Iliupersis, and Nostoi) are not treated comprehensively, they enter into the discussion at various points.
    [Show full text]
  • Strong Voices, Active Choices
    STRONG VOICES, ACTIVE CHOICES TNC’s Practitioner Framework to Strengthen Outcomes for People and Nature We would like to thank the more than 100 staff members who participated in the survey titled “Tracing TNC’s Roots in Indigenous Peoples and Local Community-led Conservation,” which provided the basis for our understanding of TNC’s work in this field, and emphasized the value of tools and guidance such as this. Further, we would like to thank the staff who engaged in the Conservation in Partnership with Indigenous Peoples and Local Communities strategy development process, from which the overarching theory of change evolved. Finally, we would like to thank the staff who contributed to this guide through their input, expertise, peer review, provision and vetting of tools and resources, and provision of case studies, particularly: Matt Brown, Laurel Chun, Rane Cortez, Eric Delvin, James Fitzsimmons, David Hinchley, Andrew Ingles, Allison Martin, Patricia Mupeta, Luke Preece, Helcio Souza, and Heather Wishik. This framework was made possible thanks to support from The Boeing Company and other generous donors. Edited and curated by Nicole R. DeMello and Erin Myers Madeira. Designed by Epstein Creative Group. Preferred Citation: The Nature Conservancy. 2017. Strong Voices, Active Choices: TNC’s Practitioner Framework to Strengthen Outcomes for People and Nature. Arlington, VA. STRONG VOICES, ACTIVE CHOICES TNC’s Practitioner Framework to Strengthen Outcomes for People and Nature FRAMEWORK PURPOSE AND NAVIGATION This framework describes The
    [Show full text]
  • Atlas (87 Km) and Hercules (71 Km) – Are a Crater Pair of Nearly the Same Size, but with Completely Different Crater Floors
    Atlas (87 km) and Hercules (71 km) – are a crater pair of nearly the same size, but with completely different crater floors. Atlas is a "Floor Fractured crater" with a system of rilles and pyroclastic ash deposits. Hercules shows a young, smooth crater floor, flooded with mare lava. Boussingault (128km) is close to the south pole of the moon. For its observation a favourable libration is needed. It is a double crater, the second crater, half the size of Boussingault, is located eccentric to the middle. Cleomedes is a crater north of Mare Crisium with a diameter of 130 km. His narrow system of rilles is difficult to observe because of the distortion at the lunar edge. On the crater floor are some small Dark Halo craters. The crater Tralles (43km) lies on the northwestern crater rim. Its impact produced major boulders on the floor of Cleomedes. Crozier H is with a diameter of 11 kilometers, the second largest concentric double crater on the front of the moon. The largest is Hesiodus A which lies on the edge of the Mare Nubium. Daguerre (45 km) is an almost entirely lava flooded crater with strange concentric ridge remnants and dark pyroclastic ash deposits. Maybe Daguerre and the complete region is of volcanic origin. Endymion, 122 km in diameter, is a Plato-like crater with smooth lava on the crater floor. Fabricius (80 km) differs in its appearance from the normal standard crater model, because it has two central mountain massives, one of them far from the middle of the crater. Furnerius (135 km) is smaller and significantly older than Petavius.
    [Show full text]
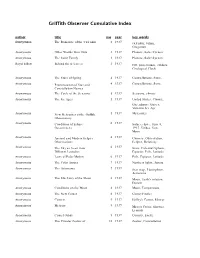
  • Griffith Observer Cumulative Index
    Griffith Observer Cumulative Index author title mo year key words Anonymous The Romance of the Calendar 2 1937 calendar, Julian, Gregorian Anonymous Other Worlds than Ours 3 1937 Planets, Solar System Anonymous The S ola r Fa mily 3 1937 Planets, Solar System Roya l Elliott Behind the Sciences 3 1937 GO, pla ne ta rium, e xhibits , Ge ologica l Clock Anonymous The Stars of Spring 4 1937 Cons te lla tions , S ta rs , Anonymous Pronunciation of Star and 4 1937 Cons te lla tions , S ta rs Constellation Names Anonymous The Cycle of the Seasons 5 1937 Seasons, climate Anonymous The Ice Ages 5 1937 United States, Climate, Greenhouse Gases, Volcano, Ice Age Anonymous New Meteorites at the Griffith 5 1937 Meteorites Observatory Anonymous Conditions of Eclipse 6 1937 Solar eclipse, June 8, Occurrences 1937, Umbra, Sun, Moon Anonymous Ancient and Modern Eclipse 6 1937 Chinese, Observation, Observations Eclips e , Re la tivity Anonymous The Sky as Seen from 6 1937 Stars, Celestial Sphere, Different Latitudes Equator, Pole, Latitude Anonymous Laws of Polar Motion 6 1937 Pole, Equator, Latitude Anonymous The Polar Aurora 7 1937 Northern lights, Aurora Anonymous The Astrorama 7 1937 Star map, Planisphere, Astrorama Anonymous The Life Story of the Moon 8 1937 Moon, Earth's rotation, Darwin Anonymous Conditions on the Moon 8 1937 Moon, Temperature, Anonymous The New Comet 8 1937 Come t Fins le r Anonymous Comets 9 1937 Halley's Comet, Meteor Anonymous Meteors 9 1937 Meteor Crater, Shower, Leonids Anonymous Comet Orbits 9 1937 Comets, Encke Anonymous
    [Show full text]
  • Landing at Lunar Impact Craters and Basins to Determine the Bombardment of Ancient Earth
    Landing at Lunar Impact Craters and Basins to Determine the Bombardment of Ancient Earth David A. Kring USRA – Lunar and Planetary Institute 72395 Apollo 17, Station 2 3.893 ± 0.016 Ga Crew: Jack Schmitt & Gene Cernan (Dalrymple & Ryder, 1996) Panorama assembled by David Harland Lunar History Orbital perspective (e.g., based on Lunar Orbiter data) Provides relative ages Based on: ● Stratigraphy of overlapping impact ejecta blankets and lava flows ● Relative densities of impact craters on surfaces Jack Schmitt – Apollo 17 Nectarian and Early Imbrian Impact Basins Impact Basin Diameter (km) Age (Ga) Orientale 930 3.82 – 3.85 ? Schrödinger 320 Early Basins Imbrian Imbrium 1,200 3.85 ± 0.01 Bailly 300 Sikorsky-Rittenhouse 310 Hertzprung 570 Serenitatis 740 3.895 ± 0.017 Crisium 1,060 3.89 ? Humorum 820 Humboldtianum 700 implying Medeleev 330 ~70 to 90 million year Nectarian Basins Nectarian Korolev 440 bombardment Moscovienese 445 Mendel-Rydberg 630 Nectaris 860 3.89 – 3.91 ? For comparison, Chicxulub’s diameter is ~180 km >1700 craters and basins 20 to >1000 km in diameter were produced The Apollo Legacy – The radiometric ages of rocks from the lunar highlands indicated the lunar crust had been thermally metamorphosed ~3.9 – 4.0 Ga. A large number of impact melts were also generated at the same time. This effect was seen in the Ar-Ar system (Turner et al., 1973) and the U-Pb system (Tera et al., 1974). It was also preserved in the more easily reset Rb-Sr system. (Data summary, left, from Bogard, 1995.) A severe period of bombardment was inferred: The lunar cataclysm hypothesis.
    [Show full text]