Lecture 25 Fall 2019 Instructor: B&S Last Time
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Lecture 26 Fall 2019 Instructors: B&S Administrative Details
CSCI 136 Data Structures & Advanced Programming Lecture 26 Fall 2019 Instructors: B&S Administrative Details • Lab 9: Super Lexicon is online • Partners are permitted this week! • Please fill out the form by tonight at midnight • Lab 6 back 2 2 Today • Lab 9 • Efficient Binary search trees (Ch 14) • AVL Trees • Height is O(log n), so all operations are O(log n) • Red-Black Trees • Different height-balancing idea: height is O(log n) • All operations are O(log n) 3 2 Implementing the Lexicon as a trie There are several different data structures you could use to implement a lexicon— a sorted array, a linked list, a binary search tree, a hashtable, and many others. Each of these offers tradeoffs between the speed of word and prefix lookup, amount of memory required to store the data structure, the ease of writing and debugging the code, performance of add/remove, and so on. The implementation we will use is a special kind of tree called a trie (pronounced "try"), designed for just this purpose. A trie is a letter-tree that efficiently stores strings. A node in a trie represents a letter. A path through the trie traces out a sequence ofLab letters that9 represent : Lexicon a prefix or word in the lexicon. Instead of just two children as in a binary tree, each trie node has potentially 26 child pointers (one for each letter of the alphabet). Whereas searching a binary search tree eliminates half the words with a left or right turn, a search in a trie follows the child pointer for the next letter, which narrows the search• Goal: to just words Build starting a datawith that structure letter. -

Balanced Trees Part One
Balanced Trees Part One Balanced Trees ● Balanced search trees are among the most useful and versatile data structures. ● Many programming languages ship with a balanced tree library. ● C++: std::map / std::set ● Java: TreeMap / TreeSet ● Many advanced data structures are layered on top of balanced trees. ● We’ll see several later in the quarter! Where We're Going ● B-Trees (Today) ● A simple type of balanced tree developed for block storage. ● Red/Black Trees (Today/Thursday) ● The canonical balanced binary search tree. ● Augmented Search Trees (Thursday) ● Adding extra information to balanced trees to supercharge the data structure. Outline for Today ● BST Review ● Refresher on basic BST concepts and runtimes. ● Overview of Red/Black Trees ● What we're building toward. ● B-Trees and 2-3-4 Trees ● Simple balanced trees, in depth. ● Intuiting Red/Black Trees ● A much better feel for red/black trees. A Quick BST Review Binary Search Trees ● A binary search tree is a binary tree with 9 the following properties: 5 13 ● Each node in the BST stores a key, and 1 6 10 14 optionally, some auxiliary information. 3 7 11 15 ● The key of every node in a BST is strictly greater than all keys 2 4 8 12 to its left and strictly smaller than all keys to its right. Binary Search Trees ● The height of a binary search tree is the 9 length of the longest path from the root to a 5 13 leaf, measured in the number of edges. 1 6 10 14 ● A tree with one node has height 0. -

Trees: Binary Search Trees
COMP2012H Spring 2014 Dekai Wu Binary Trees & Binary Search Trees (data structures for the dictionary ADT) Outline } Binary tree terminology } Tree traversals: preorder, inorder and postorder } Dictionary and binary search tree } Binary search tree operations } Search } min and max } Successor } Insertion } Deletion } Tree balancing issue COMP2012H (BST) Binary Tree Terminology } Go to the supplementary notes COMP2012H (BST) Linked Representation of Binary Trees } The degree of a node is the number of children it has. The degree of a tree is the maximum of its element degree. } In a binary tree, the tree degree is two data } Each node has two links left right } one to the left child of the node } one to the right child of the node Left child Right child } if no child node exists for a node, the link is set to NULL root 32 32 79 42 79 42 / 13 95 16 13 95 16 / / / / / / COMP2012H (BST) Binary Trees as Recursive Data Structures } A binary tree is either empty … Anchor or } Consists of a node called the root } Root points to two disjoint binary (sub)trees Inductive step left and right (sub)tree r left right subtree subtree COMP2012H (BST) Tree Traversal is Also Recursive (Preorder example) If the binary tree is empty then Anchor do nothing Else N: Visit the root, process data L: Traverse the left subtree Inductive/Recursive step R: Traverse the right subtree COMP2012H (BST) 3 Types of Tree Traversal } If the pointer to the node is not NULL: } Preorder: Node, Left subtree, Right subtree } Inorder: Left subtree, Node, Right subtree Inductive/Recursive step } Postorder: Left subtree, Right subtree, Node template <class T> void BinaryTree<T>::InOrder( void(*Visit)(BinaryTreeNode<T> *u), template<class T> BinaryTreeNode<T> *t) void BinaryTree<T>::PreOrder( {// Inorder traversal. -

Q-Tree: a Multi-Attribute Based Range Query Solution for Tele-Immersive Framework
Q-Tree: A Multi-Attribute Based Range Query Solution for Tele-Immersive Framework Md Ahsan Arefin, Md Yusuf Sarwar Uddin, Indranil Gupta, Klara Nahrstedt Department of Computer Science University of Illinois at Urbana Champaign Illinois, USA {marefin2, mduddin2, indy, klara}@illinois.edu Abstract given in a high level description which are transformed into multi-attribute composite range queries. Some of the Users and administrators of large distributed systems are examples include “which site is highly congested?”, “which frequently in need of monitoring and management of its components are not working properly?” etc. To answer the various components, data items and resources. Though there first one, the query is transformed into a multi-attribute exist several distributed query and aggregation systems, the composite range query with constrains (range of values) on clustered structure of tele-immersive interactive frameworks CPU utilization, memory overhead, stream rate, bandwidth and their time-sensitive nature and application requirements utilization, delay and packet loss rate. The later one can represent a new class of systems which poses different chal- be answered by constructing a multi-attribute range query lenges on this distributed search. Multi-attribute composite with constrains on static and dynamic characteristics of range queries are one of the key features in this class. those components. Queries can also be made by defining Queries are given in high level descriptions and then trans- different multi-attribute ranges explicitly. Another mention- formed into multi-attribute composite range queries. Design- able property of such systems is that the number of site is ing such a query engine with minimum traffic overhead, low limited due to limited display space and limited interactions, service latency, and with static and dynamic nature of large but the number of data items to store and manage can datasets, is a challenging task. -

Search Trees
Lecture III Page 1 “Trees are the earth’s endless effort to speak to the listening heaven.” – Rabindranath Tagore, Fireflies, 1928 Alice was walking beside the White Knight in Looking Glass Land. ”You are sad.” the Knight said in an anxious tone: ”let me sing you a song to comfort you.” ”Is it very long?” Alice asked, for she had heard a good deal of poetry that day. ”It’s long.” said the Knight, ”but it’s very, very beautiful. Everybody that hears me sing it - either it brings tears to their eyes, or else -” ”Or else what?” said Alice, for the Knight had made a sudden pause. ”Or else it doesn’t, you know. The name of the song is called ’Haddocks’ Eyes.’” ”Oh, that’s the name of the song, is it?” Alice said, trying to feel interested. ”No, you don’t understand,” the Knight said, looking a little vexed. ”That’s what the name is called. The name really is ’The Aged, Aged Man.’” ”Then I ought to have said ’That’s what the song is called’?” Alice corrected herself. ”No you oughtn’t: that’s another thing. The song is called ’Ways and Means’ but that’s only what it’s called, you know!” ”Well, what is the song then?” said Alice, who was by this time completely bewildered. ”I was coming to that,” the Knight said. ”The song really is ’A-sitting On a Gate’: and the tune’s my own invention.” So saying, he stopped his horse and let the reins fall on its neck: then slowly beating time with one hand, and with a faint smile lighting up his gentle, foolish face, he began.. -

Comparison of Dictionary Data Structures
A Comparison of Dictionary Implementations Mark P Neyer April 10, 2009 1 Introduction A common problem in computer science is the representation of a mapping between two sets. A mapping f : A ! B is a function taking as input a member a 2 A, and returning b, an element of B. A mapping is also sometimes referred to as a dictionary, because dictionaries map words to their definitions. Knuth [?] explores the map / dictionary problem in Volume 3, Chapter 6 of his book The Art of Computer Programming. He calls it the problem of 'searching,' and presents several solutions. This paper explores implementations of several different solutions to the map / dictionary problem: hash tables, Red-Black Trees, AVL Trees, and Skip Lists. This paper is inspired by the author's experience in industry, where a dictionary structure was often needed, but the natural C# hash table-implemented dictionary was taking up too much space in memory. The goal of this paper is to determine what data structure gives the best performance, in terms of both memory and processing time. AVL and Red-Black Trees were chosen because Pfaff [?] has shown that they are the ideal balanced trees to use. Pfaff did not compare hash tables, however. Also considered for this project were Splay Trees [?]. 2 Background 2.1 The Dictionary Problem A dictionary is a mapping between two sets of items, K, and V . It must support the following operations: 1. Insert an item v for a given key k. If key k already exists in the dictionary, its item is updated to be v. -
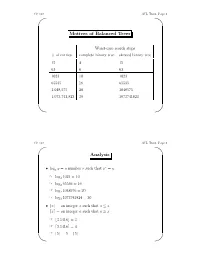
AVL Trees, Page 1 ' $
CS 310 AVL Trees, Page 1 ' $ Motives of Balanced Trees Worst-case search steps #ofentries complete binary tree skewed binary tree 15 4 15 63 6 63 1023 10 1023 65535 16 65535 1,048,575 20 1048575 1,073,741,823 30 1073741823 & % CS 310 AVL Trees, Page 2 ' $ Analysis r • logx y =anumberr such that x = y ☞ log2 1024 = 10 ☞ log2 65536 = 16 ☞ log2 1048576 = 20 ☞ log2 1073741824 = 30 •bxc = an integer a such that a ≤ x dxe = an integer a such that a ≥ x ☞ b3.1416c =3 ☞ d3.1416e =4 ☞ b5c =5=d5e & % CS 310 AVL Trees, Page 3 ' $ • If a binary search tree of N nodes happens to be complete, then a search in the tree requires at most b c log2 N +1 steps. • Big-O notation: We say f(x)=O(g(x)) if f(x)isbounded by c · g(x), where c is a constant, for sufficiently large x. ☞ x2 +11x − 30 = O(x2) (consider c =2,x ≥ 6) ☞ x100 + x50 +2x = O(2x) • If a BST happens to be complete, then a search in the tree requires O(log2 N)steps. • In a linked list of N nodes, a search requires O(N)steps. & % CS 310 AVL Trees, Page 4 ' $ AVL Trees • A balanced binary search tree structure proposed by Adelson, Velksii and Landis in 1962. • In an AVL tree of N nodes, every searching, deletion or insertion operation requires only O(log2 N)steps. • AVL tree searching is exactly the same as that of the binary search tree. & % CS 310 AVL Trees, Page 5 ' $ Definition • An empty tree is balanced. -

7. Hierarchies & Trees Visualizing Topological Relations
7. Hierarchies & Trees Visualizing topological relations Vorlesung „Informationsvisualisierung” Prof. Dr. Andreas Butz, WS 2011/12 Konzept und Basis für Folien: Thorsten Büring LMU München – Medieninformatik – Andreas Butz – Informationsvisualisierung – WS2011/12 Folie 1 Outline • Hierarchical data and tree representations • 2D Node-link diagrams – Hyperbolic Tree Browser – SpaceTree – Cheops – Degree of interest tree – 3D Node-link diagrams • Enclosure – Treemap – Ordererd Treemaps – Various examples – Voronoi treemap – 3D Treemaps • Circular visualizations • Space-filling node-link diagram LMU München – Medieninformatik – Andreas Butz – Informationsvisualisierung – WS2011/12 Folie 2 Hierarchical Data • Card et al. 1999: data repository in which data cases are related to subcases • Many data collections have an inherent hierarchical organization – Organizational Charts – Websites (approximately hierarchical) Yee et al. 2001 – File system – Family tree – OO programming • Hierarchies are usually represented as tree visual structures • Trees tend to be easier to lay out and interpret than networks (e.g. no cycles) • But: as shown in the example, networks may in some cases be visualized as a tree LMU München – Medieninformatik – Andreas Butz – Informationsvisualisierung – WS2011/12 Folie 3 Tree Representations • Two kinds of representations • Node-link diagram (see previous lecture): represent connections as edges between vertices (data cases) http://www.icann.org • Enclosure: space-filling approaches by visually nesting the hierarchy LMU -

AVL Tree, Bayer Tree, Heap Summary of the Previous Lecture
DATA STRUCTURES AND ALGORITHMS Hierarchical data structures: AVL tree, Bayer tree, Heap Summary of the previous lecture • TREE is hierarchical (non linear) data structure • Binary trees • Definitions • Full tree, complete tree • Enumeration ( preorder, inorder, postorder ) • Binary search tree (BST) AVL tree The AVL tree (named for its inventors Adelson-Velskii and Landis published in their paper "An algorithm for the organization of information“ in 1962) should be viewed as a BST with the following additional property: - For every node, the heights of its left and right subtrees differ by at most 1. Difference of the subtrees height is named balanced factor. A node with balance factor 1, 0, or -1 is considered balanced. As long as the tree maintains this property, if the tree contains n nodes, then it has a depth of at most log2n. As a result, search for any node will cost log2n, and if the updates can be done in time proportional to the depth of the node inserted or deleted, then updates will also cost log2n, even in the worst case. AVL tree AVL tree Not AVL tree Realization of AVL tree element struct AVLnode { int data; AVLnode* left; AVLnode* right; int factor; // balance factor } Adding a new node Insert operation violates the AVL tree balance property. Prior to the insert operation, all nodes of the tree are balanced (i.e., the depths of the left and right subtrees for every node differ by at most one). After inserting the node with value 5, the nodes with values 7 and 24 are no longer balanced. -

AVL Insertion, Deletion Other Trees and Their Representations
AVL Insertion, Deletion Other Trees and their representations Due now: ◦ OO Queens (One submission for both partners is sufficient) Due at the beginning of Day 18: ◦ WA8 ◦ Sliding Blocks Milestone 1 Thursday: Convocation schedule ◦ Section 01: 8:50-10:15 AM ◦ Section 02: 10:20-11:00 AM, 12:35-1:15 PM ◦ Convocation speaker Risk Analysis Pioneer John D. Graham The promise and perils of science and technology regulations 11:10 a.m. to 12:15 p.m. in Hatfield Hall. ◦ Part of Thursday's class time will be time for you to work with your partner on SlidingBlocks Due at the beginning of Day 19 : WA9 Due at the beginning of Day 21 : ◦ Sliding Blocks Final submission Non-attacking Queens Solution Insertions and Deletions in AVL trees Other Search Trees BSTWithRank WA8 Tree properties Height-balanced Trees SlidingBlocks CanAttack( ) toString( ) findNext( ) public boolean canAttack(int row, int col) { int columnDifference = col - column ; return currentRow == row || // same row currentRow == row + columnDifference || // same "down" diagonal currentRow == row - columnDifference || // same "up" diagonal neighbor .canAttack(row, col); // If I can't attack it, maybe // one of my neighbors can. } @Override public String toString() { return neighbor .toString() + " " + currentRow ; } public boolean findNext() { if (currentRow == MAXROWS ) { // no place to go until neighbors move. if (! neighbor .findNext()) return false ; // Neighbor can't move, so I can't either. currentRow = 0; // about to be bumped up to 1. } currentRow ++; return testOrAdvance(); // See if this new position works. } You did not have to write this one: // If this is a legal row for me, say so. // If not, try the next row. -

Ch04 Balanced Search Trees
Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 Ch04 Balanced Search Trees 6 v 3 8 z 4 1 1 Why care about advanced implementations? Same entries, different insertion sequence: Not good! Would like to keep tree balanced. 2 1 Balanced binary tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time needed to perform insertion and deletion and many other operations can be O(N) in the worst case We want a tree with small height A binary tree with N node has height at least (log N) Thus, our goal is to keep the height of a binary search tree O(log N) Such trees are called balanced binary search trees. Examples are AVL tree, and red-black tree. 3 Approaches to balancing trees Don't balance May end up with some nodes very deep Strict balance The tree must always be balanced perfectly Pretty good balance Only allow a little out of balance Adjust on access Self-adjusting 4 4 2 Balancing Search Trees Many algorithms exist for keeping search trees balanced Adelson-Velskii and Landis (AVL) trees (height-balanced trees) Red-black trees (black nodes balanced trees) Splay trees and other self-adjusting trees B-trees and other multiway search trees 5 5 Perfect Balance Want a complete tree after every operation Each level of the tree is full except possibly in the bottom right This is expensive For example, insert 2 and then rebuild as a complete tree 6 5 Insert 2 & 4 9 complete tree 2 8 1 5 8 1 4 6 9 6 6 3 AVL - Good but not Perfect Balance AVL trees are height-balanced binary search trees Balance factor of a node height(left subtree) - height(right subtree) An AVL tree has balance factor calculated at every node For every node, heights of left and right subtree can differ by no more than 1 Store current heights in each node 7 7 Height of an AVL Tree N(h) = minimum number of nodes in an AVL tree of height h. -

CSE 326: Data Structures B-Trees and B+ Trees
Announcements (4/30/08) • Midterm on Friday CSE 326: Data Structures • Special office hour: 4:30-5:30 Thursday in Jaech B-Trees and B+ Trees Gallery (6th floor of CSE building) – This is instead of my usual 11am office hour. Brian Curless • Reading for this lecture: Weiss Sec. 4.7 Spring 2008 2 Traversing very large datasets Memory considerations Suppose we had very many pieces of data (as in a What is in a tree node? In an object? database), e.g., n = 230 ≈ 109. Node: How many (worst case) hops through the tree to find a Object obj; node? Node left; Node right; •BST Node parent; Object: Key key; • AVL …data… Suppose the data is 1KB. How much space does the tree take? •Splay How much of the data can live in 1GB of RAM? 3 4 Cycles to access: CPU Minimizing random disk access Registers 1 In our example, almost all of our data structure is on L1 Cache 2 disk. L2 Cache 30 Thus, hopping through a tree amounts to random accesses to disk. Ouch! Main memory 250 How can we address this problem? Disk Random: 30,000,000 Streamed: 5000 5 6 M-ary Search Tree B-Trees Suppose, somehow, we devised a search tree with How do we make an M-ary search tree work? maximum branching factor M: • Each node has (up to) M-1 keys. •Order property: – subtree between two keys x and y 3 7 12 21 contain leaves with values v such that x < v < y Complete tree has height: # hops for find: x<3 3<x<7 7<x<12 12<x<21 21<x Runtime of find: 7 8 B-Tree Structure Properties B-Tree: Example Root (special case) B-Tree with M = 4 – has between 2 and M children (or root could be a