DOCSLIB.ORG

Lecture 13: AVL Trees and Binary Heaps

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Lecture 13: AVL Trees and Binary Heaps Data Structures Brett Bernstein Lecture 13: AVL Trees and Binary Heaps Review Exercises 1.( ??) Interview question: Given an array show how to shue it randomly so that any possible reordering is equally likely. static void shue(int[] arr) 2. Write a function that given the root of a binary search tree returns the node with the largest value. public static BSTNode<Integer> getLargest(BSTNode<Integer> root) 3. Explain how you would use a binary search tree to implement the Map ADT. We have included it below to remind you. Map.java //Stores a mapping of keys to values public interface Map<K,V> { //Adds key to the map with the associated value. If key already //exists, the associated value is replaced. void put(K key, V value); //Gets the value for the given key, or null if it isn't found. V get(K key); //Returns true if the key is in the map, or false otherwise. boolean containsKey(K key); //Removes the key from the map void remove(K key); //Number of keys in the map int size(); } What requirements must be placed on the Map? 4. Consider the following binary search tree. 10 5 15 1 12 18 16 17 1 Perform the following operations in order. (a) Remove 15. (b) Remove 10. (c) Add 13. (d) Add 8. 5. Suppose we begin with an empty BST. What order of add operations will yield the tallest possible tree? Review Solutions 1. One method (popular in programs like Excel) is to generate a random double corre- sponding to each element of the array, and then sort the array by the corresponding doubles. Here is a dierent method that avoids sorting (used by Collections.shue). RandomShue.java import java.util.Random; public class RandomShue { static void swap(int[] arr, int i, int j) { int tmp = arr[i]; arr[i] = arr[j]; arr[j] = tmp; } //Iterative implementation public static void shue(int[] arr) { Random ran = new Random(); for (int i = arr.length−1; i >= 1; −−i) swap(arr,i,ran.nextInt(i+1)); } //Recursive implementation public static void shueRec(int[] arr) { sRHelp(arr, arr.length, new Random()); } public static void sRHelp(int[] arr, int len, Random ran) { if (len <= 1) return; swap(arr, len−1, ran.nextInt(len)); sRHelp(arr,len−1,ran); } } 2 Above we give an iterative and a recursive implementation. We rst randomly choose one of the elements and swap it into the nal position. Then we repeat the process on the rst n − 1 elements (i.e., randomly choose last element, and then randomly shue rst n − 1 elements). 2. public static BSTNode<Integer> getLargest(BSTNode<Integer> root) { while (root.getRight() != null) root = root.getRight(); return root; } 3. We require the keys of the Map to be Comparable or a Comparator to be provided. In each node instead of simply storing a value, store a key-value pair (i.e., an entry). The BST will be ordered by the keys. Here all operations above will be Θ(h) in the worst case (we don't have containsValue above which would always be Θ(n)). In a moment, we will show how to achieve Θ(lg n) height trees which gives an ecient Map implementation without needing a hash function (but we need ordered keys). 4. (a) 10 5 16 1 12 18 17 (b) 12 5 16 1 18 17 (c) 12 5 16 131 18 17 (d) 3 12 5 16 1318 18 17 5. Ascending or descending order (i.e., sorted or reverse sorted). Data Structure: AVL Tree We have learned how to store values in a BST data structure that supports adding, removal, and searching in time Θ(h), where h is the height of the tree. We have also seen that in the worst case, the height can be Θ(n), the size of the tree. If we can keep the tree fairly balanced, then we can reduce the height to Θ(lg n) and obtain a fairly ecient data structure. To maintain a balanced structure we will use a technique invented by Adelson-Velskii and Landis (hence the name AVL tree). The idea is to keep a counter in every node (called a balance factor) that measures the dierence between the heights of the left and right subtrees (right minus left). We will add the following added constraint on our BST No balance factor will be greater than 1 or less than -1. Any BST that satises this constraint will have Θ(lg n) height. Every time we add or remove a node we may violate this constraint. To return the tree to balance we will employ a technique called a rotation. Consider the following AVL tree: 10 +1 5 15 -1 +1 1 12 20 0 0 -1 17 0 Each node has the value and balance factor in it. Now suppose we add 16 (just as we would in a BST). 4 10 +2 5 15 -1 +2 1 12 20 0 0 -2 17 -1 16 0 As you can see, the tree now violates our constraints on the balance factors. To remedy the issue, we nd the closest (lowest) ancestor of the newly added node that is out of balance. In this case, it would be the node containing the 20. We then perform a rotation so that 17 takes the place of 20, and 20 becomes the right child of 17. The resulting tree is 10 +1 5 15 -1 +1 1 12 17 0 0 0 16 20 0 0 Now the tree satises the constraint again. Let's generalize this example to all possible ways adding a node can imbalance the tree. First notice that if adding a value will cause a node to violate its balance factor constraint, then it must have been −1 or +1 already, since adding a single node can add at most 1 to the height of any subtree. Let's assume a node currently has balance factor −1 and some value X. We will model the possible ways that the node containing X will be the lowest node that violates the balance factor constraint (by adding values). 5 X -1 Y 0 C k k A B k Above Y < X and all of the labeled subtrees have the same height k ≥ 0. The subtree rooted at X has height k + 1. We rst handle the case that a node is added to subtree A that increases its height. X -2 Y -1 Z C k B k A1 A2 Here we assumed the value added was smaller than Y . Note that the subtree rooted at X now has height k + 2. We then zoom in on the subtree A by drawing its root Z and subtrees A1 and A2. The possible heights of A1;A2 are (this will not eect our course of action though): 1. If k = 0 then A1;A2 are both empty. Z has a balance factor of 0 2. If k > 0 and the new value is smaller than Z then A1 has height k and A2 has height k − 1. Z has a balance factor of −1. 3. If k > 0 and the new value is greater than Z then A1 has height k − 1 and A2 has height k. Z has a balance factor of +1. To x this we perform a rotation that puts Y where X is: 6 Y 0 ZX 0 A1 A2 BC k The balance constraints are no longer violated. Note that the subtree rooted at Y has height k + 1, the same as the subtree rooted at X before a value was added. Thus all nodes above Y in the tree are now balanced as well. This is the so called left-left case since Z is the left child of Y which is the left child of X. The other left-right case occurs when we add a value that is larger than Y to our original tree (the picture with A, B, and C) above. X -2 Y +1 W C k k A B1 B2 Here we have zoomed in on the subtree B. We have similar cases as above that determine the heights of B1;B2. Here we perform a rotation that puts W in place of Y : X -2 W Y C k B2 k A B1 This gives us a case like the left-left situation. Thus we perform a second rotation as above putting W in place of X: 7 W 0 YX k A B1 B2 C k Again we have restored balance and the resulting tree has height k + 1. Thus all ancestors of W are balanced too. Using the operations above and their reections (right-right and right-left cases) we can enforce the balance constraints on every add operation. The TreeMap and TreeSet in Java use a related data structure called a red-black tree that uses a slightly dierent constraint for balance, but also uses rotations to enforce the constraint. AVL Tree Exercises 1. Consider the following BST. 10 5 15 6 12 (a) Add balance factors to all of the nodes. (b) Show what happens when we add the node 13 (treating the tree as an AVL tree). (c) Next add 7 to the tree (treating the tree as an AVL tree). (d)( ?) Next delete 5, 7, and 6 from the tree. Make sure to remedy any violated balance constraints. 2. Give a simple Θ(n lg n) sorting algorithm assuming you have access to an AVL Tree data structure. 3.( ??) The AVL Tree deletion algorithm is similar to the addition algorithm, but can cause as many as Θ(h) rotations to occur where h is the height of the tree.
Load more

Recommended publications
  • Lecture 26 Fall 2019 Instructors: B&S Administrative Details
    CSCI 136 Data Structures & Advanced Programming Lecture 26 Fall 2019 Instructors: B&S Administrative Details • Lab 9: Super Lexicon is online • Partners are permitted this week! • Please fill out the form by tonight at midnight • Lab 6 back 2 2 Today • Lab 9 • Efficient Binary search trees (Ch 14) • AVL Trees • Height is O(log n), so all operations are O(log n) • Red-Black Trees • Different height-balancing idea: height is O(log n) • All operations are O(log n) 3 2 Implementing the Lexicon as a trie There are several different data structures you could use to implement a lexicon— a sorted array, a linked list, a binary search tree, a hashtable, and many others. Each of these offers tradeoffs between the speed of word and prefix lookup, amount of memory required to store the data structure, the ease of writing and debugging the code, performance of add/remove, and so on. The implementation we will use is a special kind of tree called a trie (pronounced "try"), designed for just this purpose. A trie is a letter-tree that efficiently stores strings. A node in a trie represents a letter. A path through the trie traces out a sequence ofLab letters that9 represent : Lexicon a prefix or word in the lexicon. Instead of just two children as in a binary tree, each trie node has potentially 26 child pointers (one for each letter of the alphabet). Whereas searching a binary search tree eliminates half the words with a left or right turn, a search in a trie follows the child pointer for the next letter, which narrows the search• Goal: to just words Build starting a datawith that structure letter.
    [Show full text]
  • Game Trees, Quad Trees and Heaps
    CS 61B Game Trees, Quad Trees and Heaps Fall 2014 1 Heaps of fun R (a) Assume that we have a binary min-heap (smallest value on top) data structue called Heap that stores integers and has properly implemented insert and removeMin methods. Draw the heap and its corresponding array representation after each of the operations below: Heap h = new Heap(5); //Creates a min-heap with 5 as the root 5 5 h.insert(7); 5,7 5 / 7 h.insert(3); 3,7,5 3 /\ 7 5 h.insert(1); 1,3,5,7 1 /\ 3 5 / 7 h.insert(2); 1,2,5,7,3 1 /\ 2 5 /\ 7 3 h.removeMin(); 2,3,5,7 2 /\ 3 5 / 7 CS 61B, Fall 2014, Game Trees, Quad Trees and Heaps 1 h.removeMin(); 3,7,5 3 /\ 7 5 (b) Consider an array based min-heap with N elements. What is the worst case running time of each of the following operations if we ignore resizing? What is the worst case running time if we take into account resizing? What are the advantages of using an array based heap vs. using a BST-based heap? Insert O(log N) Find Min O(1) Remove Min O(log N) Accounting for resizing: Insert O(N) Find Min O(1) Remove Min O(N) Using a BST is not space-efficient. (c) Your friend Alyssa P. Hacker challenges you to quickly implement a max-heap data structure - "Hah! I’ll just use my min-heap implementation as a template", you think to yourself.
    [Show full text]
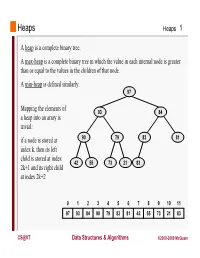
  • Heaps a Heap Is a Complete Binary Tree. a Max-Heap Is A
    Heaps Heaps 1 A heap is a complete binary tree. A max-heap is a complete binary tree in which the value in each internal node is greater than or equal to the values in the children of that node. A min-heap is defined similarly. 97 Mapping the elements of 93 84 a heap into an array is trivial: if a node is stored at 90 79 83 81 index k, then its left child is stored at index 42 55 73 21 83 2k+1 and its right child at index 2k+2 01234567891011 97 93 84 90 79 83 81 42 55 73 21 83 CS@VT Data Structures & Algorithms ©2000-2009 McQuain Building a Heap Heaps 2 The fact that a heap is a complete binary tree allows it to be efficiently represented using a simple array. Given an array of N values, a heap containing those values can be built, in situ, by simply “sifting” each internal node down to its proper location: - start with the last 73 73 internal node * - swap the current 74 81 74 * 93 internal node with its larger child, if 79 90 93 79 90 81 necessary - then follow the swapped node down 73 * 93 - continue until all * internal nodes are 90 93 90 73 done 79 74 81 79 74 81 CS@VT Data Structures & Algorithms ©2000-2009 McQuain Heap Class Interface Heaps 3 We will consider a somewhat minimal maxheap class: public class BinaryHeap<T extends Comparable<? super T>> { private static final int DEFCAP = 10; // default array size private int size; // # elems in array private T [] elems; // array of elems public BinaryHeap() { .
    [Show full text]
  • L11: Quadtrees CSE373, Winter 2020
    L11: Quadtrees CSE373, Winter 2020 Quadtrees CSE 373 Winter 2020 Instructor: Hannah C. Tang Teaching Assistants: Aaron Johnston Ethan Knutson Nathan Lipiarski Amanda Park Farrell Fileas Sam Long Anish Velagapudi Howard Xiao Yifan Bai Brian Chan Jade Watkins Yuma Tou Elena Spasova Lea Quan L11: Quadtrees CSE373, Winter 2020 Announcements ❖ Homework 4: Heap is released and due Wednesday ▪ Hint: you will need an additional data structure to improve the runtime for changePriority(). It does not affect the correctness of your PQ at all. Please use a built-in Java collection instead of implementing your own. ▪ Hint: If you implemented a unittest that tested the exact thing the autograder described, you could run the autograder’s test in the debugger (and also not have to use your tokens). ❖ Please look at posted QuickCheck; we had a few corrections! 2 L11: Quadtrees CSE373, Winter 2020 Lecture Outline ❖ Heaps, cont.: Floyd’s buildHeap ❖ Review: Set/Map data structures and logarithmic runtimes ❖ Multi-dimensional Data ❖ Uniform and Recursive Partitioning ❖ Quadtrees 3 L11: Quadtrees CSE373, Winter 2020 Other Priority Queue Operations ❖ The two “primary” PQ operations are: ▪ removeMax() ▪ add() ❖ However, because PQs are used in so many algorithms there are three common-but-nonstandard operations: ▪ merge(): merge two PQs into a single PQ ▪ buildHeap(): reorder the elements of an array so that its contents can be interpreted as a valid binary heap ▪ changePriority(): change the priority of an item already in the heap 4 L11: Quadtrees CSE373,
    [Show full text]
  • Search Trees
    Lecture III Page 1 “Trees are the earth’s endless effort to speak to the listening heaven.” – Rabindranath Tagore, Fireflies, 1928 Alice was walking beside the White Knight in Looking Glass Land. ”You are sad.” the Knight said in an anxious tone: ”let me sing you a song to comfort you.” ”Is it very long?” Alice asked, for she had heard a good deal of poetry that day. ”It’s long.” said the Knight, ”but it’s very, very beautiful. Everybody that hears me sing it - either it brings tears to their eyes, or else -” ”Or else what?” said Alice, for the Knight had made a sudden pause. ”Or else it doesn’t, you know. The name of the song is called ’Haddocks’ Eyes.’” ”Oh, that’s the name of the song, is it?” Alice said, trying to feel interested. ”No, you don’t understand,” the Knight said, looking a little vexed. ”That’s what the name is called. The name really is ’The Aged, Aged Man.’” ”Then I ought to have said ’That’s what the song is called’?” Alice corrected herself. ”No you oughtn’t: that’s another thing. The song is called ’Ways and Means’ but that’s only what it’s called, you know!” ”Well, what is the song then?” said Alice, who was by this time completely bewildered. ”I was coming to that,” the Knight said. ”The song really is ’A-sitting On a Gate’: and the tune’s my own invention.” So saying, he stopped his horse and let the reins fall on its neck: then slowly beating time with one hand, and with a faint smile lighting up his gentle, foolish face, he began..
    [Show full text]
  • Comparison of Dictionary Data Structures
    A Comparison of Dictionary Implementations Mark P Neyer April 10, 2009 1 Introduction A common problem in computer science is the representation of a mapping between two sets. A mapping f : A ! B is a function taking as input a member a 2 A, and returning b, an element of B. A mapping is also sometimes referred to as a dictionary, because dictionaries map words to their definitions. Knuth [?] explores the map / dictionary problem in Volume 3, Chapter 6 of his book The Art of Computer Programming. He calls it the problem of 'searching,' and presents several solutions. This paper explores implementations of several different solutions to the map / dictionary problem: hash tables, Red-Black Trees, AVL Trees, and Skip Lists. This paper is inspired by the author's experience in industry, where a dictionary structure was often needed, but the natural C# hash table-implemented dictionary was taking up too much space in memory. The goal of this paper is to determine what data structure gives the best performance, in terms of both memory and processing time. AVL and Red-Black Trees were chosen because Pfaff [?] has shown that they are the ideal balanced trees to use. Pfaff did not compare hash tables, however. Also considered for this project were Splay Trees [?]. 2 Background 2.1 The Dictionary Problem A dictionary is a mapping between two sets of items, K, and V . It must support the following operations: 1. Insert an item v for a given key k. If key k already exists in the dictionary, its item is updated to be v.
    [Show full text]
  • AVL Tree, Bayer Tree, Heap Summary of the Previous Lecture
    DATA STRUCTURES AND ALGORITHMS Hierarchical data structures: AVL tree, Bayer tree, Heap Summary of the previous lecture • TREE is hierarchical (non linear) data structure • Binary trees • Definitions • Full tree, complete tree • Enumeration ( preorder, inorder, postorder ) • Binary search tree (BST) AVL tree The AVL tree (named for its inventors Adelson-Velskii and Landis published in their paper "An algorithm for the organization of information“ in 1962) should be viewed as a BST with the following additional property: - For every node, the heights of its left and right subtrees differ by at most 1. Difference of the subtrees height is named balanced factor. A node with balance factor 1, 0, or -1 is considered balanced. As long as the tree maintains this property, if the tree contains n nodes, then it has a depth of at most log2n. As a result, search for any node will cost log2n, and if the updates can be done in time proportional to the depth of the node inserted or deleted, then updates will also cost log2n, even in the worst case. AVL tree AVL tree Not AVL tree Realization of AVL tree element struct AVLnode { int data; AVLnode* left; AVLnode* right; int factor; // balance factor } Adding a new node Insert operation violates the AVL tree balance property. Prior to the insert operation, all nodes of the tree are balanced (i.e., the depths of the left and right subtrees for every node differ by at most one). After inserting the node with value 5, the nodes with values 7 and 24 are no longer balanced.
    [Show full text]
  • Leftist Heap: Is a Binary Tree with the Normal Heap Ordering Property, but the Tree Is Not Balanced. in Fact It Attempts to Be Very Unbalanced!
    Leftist heap: is a binary tree with the normal heap ordering property, but the tree is not balanced. In fact it attempts to be very unbalanced! Definition: the null path length npl(x) of node x is the length of the shortest path from x to a node without two children. The null path lengh of any node is 1 more than the minimum of the null path lengths of its children. (let npl(nil)=-1). Only the tree on the left is leftist. Null path lengths are shown in the nodes. Definition: the leftist heap property is that for every node x in the heap, the null path length of the left child is at least as large as that of the right child. This property biases the tree to get deep towards the left. It may generate very unbalanced trees, which facilitates merging! It also also means that the right path down a leftist heap is as short as any path in the heap. In fact, the right path in a leftist tree of N nodes contains at most lg(N+1) nodes. We perform all the work on this right path, which is guaranteed to be short. Merging on a leftist heap. (Notice that an insert can be considered as a merge of a one-node heap with a larger heap.) 1. (Magically and recursively) merge the heap with the larger root (6) with the right subheap (rooted at 8) of the heap with the smaller root, creating a leftist heap. Make this new heap the right child of the root (3) of h1.
    [Show full text]
  • Data Structures and Programming Spring 2016, Final Exam
    Data Structures and Programming Spring 2016, Final Exam. June 21, 2016 1 1. (15 pts) True or False? (Mark for True; × for False. Score = maxf0, Right - 2 Wrongg. No explanations are needed. (1) Let A1;A2, and A3 be three sorted arrays of n real numbers (all distinct). In the comparison model, constructing a balanced binary search tree of the set A1 [ A2 [ A3 requires Ω(n log n) time. × False (Merge A1;A2;A3 in linear time; then pick recursively the middle as root (in linear time).) (2) Let T be a complete binary tree with n nodes. Finding a path from the root of T to a given vertex v 2 T using breadth-first search takes O(log n) time. × False (Note that the tree is NOT a search tree.) (3) Given an unsorted array A[1:::n] of n integers, building a max-heap out of the elements of A can be performed asymptotically faster than building a red-black tree out of the elements of A. True (O(n) for building a max-heap; Ω(n log n) for building a red-black tree.) (4) In the worst case, a red-black tree insertion requires O(1) rotations. True (See class notes) (5) In the worst case, a red-black tree deletion requires O(1) node recolorings. × False (See class notes) (6) Building a binomial heap from an unsorted array A[1:::n] takes O(n) time. True (See class notes) (7) Insertion into an AVL tree asymptotically beats insertion into an AA-tree. × False (See class notes) (8) The subtree of the root of a red-black tree is always itself a red-black tree.
    [Show full text]
  • Heapsort Previous Sorting Algorithms G G Heap Data Structure P Balanced
    Previous sortinggg algorithms Insertion Sort 2 O(n ) time Heapsort Merge Sort Based off slides by: David Matuszek http://www.cis.upenn.edu/~matuszek/cit594-2008/ O(n) space PtdbMttBPresented by: Matt Boggus 2 Heap data structure Balanced binary trees Binary tree Recall: The dthfdepth of a no de iitditis its distance f rom th e root The depth of a tree is the depth of the deepest node Balanced A binary tree of depth n is balanced if all the nodes at depths 0 through n-2 have two children Left-justified n-2 (Max) Heap property: no node has a value greater n-1 than the value in its parent n Balanced Balanced Not balanced 3 4 Left-jjyustified binary trees Buildinggp up to heap sort How to build a heap A balanced binary tree of depth n is left- justified if: n it has 2 nodes at depth n (the tree is “full”)or ), or k How to maintain a heap it has 2 nodes at depth k, for all k < n, and all the leaves at dept h n are as fa r le ft as poss i ble How to use a heap to sort data Left-justified Not left-justified 5 6 The heappp prop erty siftUp A node has the heap property if the value in the Given a node that does not have the heap property, you can nodide is as large as or larger t han th e va lues iiin its give it the heap property by exchanging its value with the children value of the larger child 12 12 12 12 14 8 3 8 12 8 14 8 14 8 12 Blue node has Blue node has Blue node does not Blue node does not Blue node has heap property heap property have heap property have heap property heap property All leaf nodes automatically have
    [Show full text]
  • AVL Insertion, Deletion Other Trees and Their Representations
    AVL Insertion, Deletion Other Trees and their representations Due now: ◦ OO Queens (One submission for both partners is sufficient) Due at the beginning of Day 18: ◦ WA8 ◦ Sliding Blocks Milestone 1 Thursday: Convocation schedule ◦ Section 01: 8:50-10:15 AM ◦ Section 02: 10:20-11:00 AM, 12:35-1:15 PM ◦ Convocation speaker Risk Analysis Pioneer John D. Graham The promise and perils of science and technology regulations 11:10 a.m. to 12:15 p.m. in Hatfield Hall. ◦ Part of Thursday's class time will be time for you to work with your partner on SlidingBlocks Due at the beginning of Day 19 : WA9 Due at the beginning of Day 21 : ◦ Sliding Blocks Final submission Non-attacking Queens Solution Insertions and Deletions in AVL trees Other Search Trees BSTWithRank WA8 Tree properties Height-balanced Trees SlidingBlocks CanAttack( ) toString( ) findNext( ) public boolean canAttack(int row, int col) { int columnDifference = col - column ; return currentRow == row || // same row currentRow == row + columnDifference || // same "down" diagonal currentRow == row - columnDifference || // same "up" diagonal neighbor .canAttack(row, col); // If I can't attack it, maybe // one of my neighbors can. } @Override public String toString() { return neighbor .toString() + " " + currentRow ; } public boolean findNext() { if (currentRow == MAXROWS ) { // no place to go until neighbors move. if (! neighbor .findNext()) return false ; // Neighbor can't move, so I can't either. currentRow = 0; // about to be bumped up to 1. } currentRow ++; return testOrAdvance(); // See if this new position works. } You did not have to write this one: // If this is a legal row for me, say so. // If not, try the next row.
    [Show full text]
  • Ch04 Balanced Search Trees
    Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 Ch04 Balanced Search Trees 6 v 3 8 z 4 1 1 Why care about advanced implementations? Same entries, different insertion sequence: Not good! Would like to keep tree balanced. 2 1 Balanced binary tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time needed to perform insertion and deletion and many other operations can be O(N) in the worst case We want a tree with small height A binary tree with N node has height at least (log N) Thus, our goal is to keep the height of a binary search tree O(log N) Such trees are called balanced binary search trees. Examples are AVL tree, and red-black tree. 3 Approaches to balancing trees Don't balance May end up with some nodes very deep Strict balance The tree must always be balanced perfectly Pretty good balance Only allow a little out of balance Adjust on access Self-adjusting 4 4 2 Balancing Search Trees Many algorithms exist for keeping search trees balanced Adelson-Velskii and Landis (AVL) trees (height-balanced trees) Red-black trees (black nodes balanced trees) Splay trees and other self-adjusting trees B-trees and other multiway search trees 5 5 Perfect Balance Want a complete tree after every operation Each level of the tree is full except possibly in the bottom right This is expensive For example, insert 2 and then rebuild as a complete tree 6 5 Insert 2 & 4 9 complete tree 2 8 1 5 8 1 4 6 9 6 6 3 AVL - Good but not Perfect Balance AVL trees are height-balanced binary search trees Balance factor of a node height(left subtree) - height(right subtree) An AVL tree has balance factor calculated at every node For every node, heights of left and right subtree can differ by no more than 1 Store current heights in each node 7 7 Height of an AVL Tree N(h) = minimum number of nodes in an AVL tree of height h.
    [Show full text]