Atomic Structure
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

CALENDAR 2011 Sydney.Edu.Au/Calendar Calendar 2011 Calendar 2011
CALENDAR 2011 sydney.edu.au/calendar Calendar 2011 Calendar 2011 The Arms of the University Sidere mens eadem mutato Though the constellations change, the mind is universal The Arms Numbering of resolutions The following is an extract from the document granting Arms to the Renumbering of resolutions is for convenience only and does not University, dated May 1857: affect the interpretation of the resolutions, unless the context otherwise requires. Argent on a Cross Azure an open book proper, clasps Gold, between four Stars of eight points Or, on a chief Gules a Lion passant guardant Production also Or, together with this motto "Sidere mens eadem mutato" ... to Web and Print Production, Marketing and Communications be borne and used forever hereafter by the said University of Sydney Website: sydney.edu.au/web_print on their Common Seal, Shields, or otherwise according to the Law of Arms. The University of Sydney NSW 2006 Australia The motto, which was devised by FLS Merewether, Second Vice- Phone: +61 2 9351 2222 Provost of the University, conveys the feeling that in this hemisphere Website: sydney.edu.au all feelings and attitudes to scholarship are the same as those of our CRICOS Provider Code: 00026A predecessors in the northern hemisphere. Disclaimer ISSN: 0313-4466 This publication is copyright and remains the property of the University ISBN: 978-1-74210-173-6 of Sydney. This information is valid at the time of publication and the University reserves the right to alter information contained in the Calendar. Calendar 2010 ii Contents -

Genome Stability and Human Diseases (Subcellular Biochemistry)
Genome Stability and Human Diseases SUBCELLULAR BIOCHEMISTRY SERIES EDITOR J. ROBIN HARRIS, University of Mainz, Mainz, Germany ASSISTANT EDITORS P.J. QUINN, King’s College London, London, U.K. Recent Volumes in this Series Vo l u m e 3 3 Bacterial Invasion into Eukaryotic Cells Tobias A. Oelschlaeger and Jorg Hacker Vo l u m e 3 4 Fusion of Biological Membranes and Related Problems Edited by Herwig Hilderson and Stefan Fuller Vo l u m e 3 5 Enzyme-Catalyzed Electron and Radical Transfer Andreas Holzenburg and Nigel S. Scrutton Vo l u m e 3 6 Phospholipid Metabolism in Apoptosis Edited by Peter J. Quinn and Valerian E. Kagan Vo l u m e 3 7 Membrane Dynamics and Domains Edited by P.J. Quinn Vo l u m e 3 8 Alzheimer’s Disease: Cellular and Molecular Aspects of Amyloid beta Edited by R. Harris and F. Fahrenholz Vo l u m e 3 9 Biology of Inositols and Phosphoinositides Edited by A. Lahiri Majumder and B.B. Biswas Vo l u m e 4 0 Reviews and Protocols in DT40 Research Edited by Jean-Marie Buerstedde and Shunichi Takeda Vo l u m e 4 1 Chromatin and Disease Edited by Tapas K. Kundu and Dipak Dasgupta Vo l u m e 4 2 Inflammation in the Pathogenesis of Chronic Diseases Edited by Randall E. Harris Vo l u m e 4 3 Subcellular Proteomics Edited by Eric Bertrand and Michel Faupel Vo l u m e 4 4 Peroxiredoxin Systems Edited by Leopold Flohd J. -

Mass Spectrometry-Based Proteomics Reveals Distinct Mechanisms of Astrocyte Protein Secretion
University of Pennsylvania ScholarlyCommons Publicly Accessible Penn Dissertations Summer 2009 Mass Spectrometry-Based Proteomics Reveals Distinct Mechanisms of Astrocyte Protein Secretion Todd M. Greco University of Pennsylvania, [email protected] Follow this and additional works at: https://repository.upenn.edu/edissertations Part of the Cell Biology Commons, and the Molecular and Cellular Neuroscience Commons Recommended Citation Greco, Todd M., "Mass Spectrometry-Based Proteomics Reveals Distinct Mechanisms of Astrocyte Protein Secretion" (2009). Publicly Accessible Penn Dissertations. 22. https://repository.upenn.edu/edissertations/22 This paper is posted at ScholarlyCommons. https://repository.upenn.edu/edissertations/22 For more information, please contact [email protected]. Mass Spectrometry-Based Proteomics Reveals Distinct Mechanisms of Astrocyte Protein Secretion Abstract The ability of astrocytes to secrete proteins subserves many of its known function, such as synapse formation during development and extracellular matrix remodeling after cellular injury. Protein secretion may also play an important, but less clear, role in the propagation of inflammatory responses and neurodegenerative disease pathogenesis. While potential astrocyte-secreted proteins may number in the thousands, known astrocyte-secreted proteins are less than 100. To address this fundamental deficiency, mass spectrometry-based proteomics and bioinformatic tools were utilized for global discovery, comparison, and quantification of astrocyte-secreted proteins. A primary mouse astrocyte cell culture model was used to generate a collection of astrocyte-secreted proteins termed the astrocyte secretome. A multidimensional protein and peptide separation approach paired with mass spectrometric analysis interrogated the astrocyte secretome under control and cytokine-exposed conditions, identifying cytokine- induced secreted proteins, while extending the depth of known astrocyte-secreted proteins to 169. -

Analysis of Bacterial Lipooligosaccharides by MALDI-TOF MS with Traveling Wave Ion Mobility
B American Society for Mass Spectrometry (outside the USA), 2016 J. Am. Soc. Mass Spectrom. (2016) 27:1263Y1276 DOI: 10.1007/s13361-016-1383-3 RESEARCH ARTICLE Analysis of Bacterial Lipooligosaccharides by MALDI-TOF MS with Traveling Wave Ion Mobility Nancy J. Phillips,1 Constance M. John,2,3 Gary A. Jarvis2,3 1Department of Pharmaceutical Chemistry, University of California, San Francisco, CA 94143, USA 2Center for Immunochemistry, Veterans Affairs Medical Center, 4150 Clement Street, San Francisco, CA 94121, USA 3Department of Laboratory Medicine, University of California, San Francisco, CA 94143, USA MALDI IMS-MS Abstract. Lipooligosaccharides (LOS) are major microbial virulence factors displayed on the outer membrane of rough-type Gram-negative bacteria. These amphipathic glycolipids are comprised of two domains, a core oligosaccharide linked to a lipid A LOS moiety. Isolated LOS samples are generally heterogeneous mixtures of glycoforms, with structural variability in both domains. Traditionally, the oligosaccharide and lipid OS A components of LOS have been analyzed separately following mild acid hydrolysis, 2000 4000 m/z Lipid A although important acid-labile moieties can be cleaved. Recently, an improved meth- od was introduced for analysis of intact LOS by MALDI-TOF MS using a thin layer 015 105 20 drift time (ms) matrix composed of 2,4,6-trihydroxyacetophenone (THAP) and nitrocellulose. In addition to molecular ions, the spectra show in-source Bprompt^ fragments arising from regiospecific cleavage between the lipid A and oligosaccharide domains. Here, we demonstrate the use of traveling wave ion mobility spectrometry (TWIMS) for IMS-MS and IMS-MS/MS analyses of intact LOS from Neisseria spp. -
Degree Congregations July 2016 in the Whitworth Hall “Use Your Head, but Follow Your Heart.” Nancy Rothwell Congratulations from the President and Vice-Chancellor
the University of Manchester Degree Congregations July 2016 in the Whitworth Hall “Use your head, but follow your heart.” Nancy Rothwell Congratulations from the President and Vice-Chancellor I welcome you all – graduands, family members and friends – to e University of Manchester for this degree congregation. is is a time of celebration and i hope you enjoy this special occasion. For those of you graduating today, this is also a These ceremonies mark not the end of your perfect time to reflect on your time here at relationship with the University but the start Manchester, to think about your successes, of a new chapter. You are now part of a world- achievements and the excitement of the next wide network and it is my hope that the links stage of your journey. As you are presented for between you and the University will grow conferment of your degree, the University stronger as you become an active member of shares with you a great sense of pride in the one of the largest global alumni communities. award you have worked so hard to attain. I wish you every success for the future and I encourage you to take charge of your future, hope that you have a truly memorable day. find your voice and form your own opinions. Have confidence in the knowledge and experience you have gained during your time here and, as you collect your degree, know you are ready to take on your next challenge and shape your own future. Professor Dame Nancy Rothwell DEGREE CONGREGATIONS JULY 2016 1 Our distinguished staff and alumni invest us with progressive principles and a desire Leading to improve people's lives through research and teaching. -

PSI · Scientifi C Report 2002 / Volume IV
PAUL SCHE RRE R INSTIT UT — — ISSN 1423-7334 March 2003 ) PSI · Scientifi c Report 2002 / Volume IV Nuclear Energy and Safety PAUL SCHERRER INSTITUT ISSN 1423-7334 _H^ March 2003 Scientific Report 2002 Volume IV Nuclear Energy and Safety ed. by: Brian Smith and Beatrice Gschwend CH-5232 Villigen PSI Switzerland Phone: 056/310 21 11 Telefax: 056/310 21 99 http://nes.web.psi.ch Table of Contents Introduction 3 W. Kroger Overview of Main Activities 7 K. Foskolos, W. Kroger Risk Benefits of Climate-Friendly Energy Supply Options 15 S. Hirschberg, P. Burgherr Development of Dynamic Probabilistic Safety Assessment: The Accident Dynamic Simulator (ADS) Tool 21 Y.H. Chang, A. Mosleh, V.N. Dang Level-Swell Prediciton with RETRAN-3D and its Application to a BWR Steam-Line-Break Analysis... 29 Y. Aounallah, K. Hofer RETRAN-3D Analysis of the OECD/NRC Peach Bottom 2 Turbine Trip Benchmark 41 W. Barten, P. Coddington Reactivity Measurements on Burnt and Reference Fuel Samples in LWR-PROTEUS Phase II 55 M. Murphy, F. Jatuff, P. Grimm, R. Seiler, A. Luthi, R. van Geemert, R. Brogli, R. Chawla, G. Meier, H.-D. Berger Experimental Investigation in the PANDA Facility of the Impact of a Hydrogen Release on Passive Containment Cooling Systems 61 O. Auban, D. Paladino, P. Candreia, M. Huggenberger, H.J. Strassberger CFD Simulation of Steady-State Conditions in a 1/5th-Scale Model of a Typical 3-Loop PWR in the Context of Boron Dilution Events 69 T.V. Dury Assessment of the MELCOR Code against PHEBUS Experiment FPT-1 Performed in the Frame of ISP-46 75 J. -

Calendar 2008 Calendar 2008
Calendar 2008 Calendar Calendar 2008 RRP $20.00 (includes GST) Produced by the Digital and Print Media Office of the University of Sydney, 2008 CRICOS Provider No. 00026A 1517/08 Calendar 2008 Calendar 2008 i Calendar 2008 Disclaimer This publication is copyright and remains the property of the University of Sydney. This information is valid at the time of publication and the University reserves the right to alter information contained in the Calendar. Updates Sidere mens eadem mutato All updates and approved amendments to the information in the 2008 Though the constellation may change Calendar can be found at www.usyd.edu.au/calendar the spirit remains the same Numbering of Resolutions Renumbering of Resolutions is for convenience only and does not affect the interpretation of the Resolutions, unless the context The Arms otherwise requires. The following is an extract from the document granting Arms to the University, dated May 1857: Argent on a Cross Azure an open book proper, clasps Gold, between The University of Sydney four Stars of eight points Or, on a chief Gules a Lion passant guardant NSW 2006 Australia also Or, together with this motto "Sidere mens eadem mutato" ... to Phone: +61 2 9351 2222 be borne and used forever hereafter by the said University of SYDNEY Website: www.usyd.edu.au on their Common Seal, Shields, or otherwise according to the Law of Arms. Production The motto, which was devised by F L S Merewether, Second Vice-Provost of the University, conveys the feeling that in this Digital and Print Media Office hemisphere all feelings and attitudes to scholarship are the same as Website: www.usyd.edu.au/digital_print_media those of our predecessors in the northern hemisphere. -

Investigation of Cancerous Tissues by MALDI Mass Spectrometry Imaging - Imaging of Proteolytic Activity in Frozen Tissue and Standardised On- Tissue Digestion
Aus dem Institut für Medizintechnologie der Universität Heidelberg und der Hochschule Mannheim (Geschäftsführender Direktor: Prof. Dr. med. Norbert Gretz) Investigation of Cancerous Tissues by MALDI Mass Spectrometry Imaging - Imaging of proteolytic activity in frozen tissue and standardised on- tissue digestion Inauguraldissertation zur Erlangung des akademischen Grades Doctor scientiarum humanarum (Dr. sc. hum.) der Medizinischen Fakultät Mannheim der Ruprecht-Karls-Universität zu Heidelberg vorgelegt von Katrin Miriam Erich aus Bad Dürkheim a.d.W. 2019 Dekan: Prof. Dr. med. Sergij Goerdt Referent: Prof. Dr. rer. nat. Carsten Hopf Für meine Tochter und meinen Ehemann, die viel Zeit opferten und mich stets unterstützen… TABLE OF CONTENT Page ABBREVIATIONS ....................................................................................................... 1 1 INTRODUCTION .................................................................................................... 3 1.1 Classification of Proteases ............................................................................ 3 1.1.1 The role of proteases in disease ................................................................... 5 1.1.2 Relevant proteases in gastric cancer ............................................................ 6 1.2 Visualization of protease activity.................................................................... 8 1.3 Mass Spectrometry ........................................................................................ 9 1.3.1 The principle of -

Supplement 2002 04
HMI-B 5xx Annual Report2002 Supplement tothe Invited Lectures HMI, Annual Report 2002 Supplement to the Annual Report 2002 Berlin 2003 Annual Report 2002 A 1 HMI, Annual Report 2002 Supplement Index Publications .......................................................................................................... A 3 SF – Structure and Dynamics in Condensed Matter ........................................................... A 4 SE – Solar Energy Research............................................................................................ A 24 HAD – Information Technology ........................................................................................ A 35 Conference Contributions ................................................................................. A 37 SF – Structure and Dynamics in Condensed Matter ......................................................... A 38 SE – Solar Energy Research............................................................................................ A 64 HAD – Information Technology ........................................................................................ A 78 Invited Lectures .................................................................................................. A 79 SF – Structure and Dynamics in Condensed Matter ......................................................... A 80 SE – Solar Energy Research............................................................................................ A 87 HAD – Information Technology ....................................................................................... -

Mind Ergonomy for the Knowledge Economy : Software Neuroergonomics and Biomimetics for the Knowledge Economy
Mind Ergonomy for the Knowledge Economy : software Neuroergonomics and Biomimetics for the Knowledge Economy. Why? How? What? Idriss Jamil Aberkane To cite this version: Idriss Jamil Aberkane. Mind Ergonomy for the Knowledge Economy : software Neuroergonomics and Biomimetics for the Knowledge Economy. Why? How? What?. Cognitive Sciences. Université Paris Saclay (COmUE), 2016. English. NNT : 2016SACLX005. tel-03130253 HAL Id: tel-03130253 https://pastel.archives-ouvertes.fr/tel-03130253 Submitted on 3 Feb 2021 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. NNT : 2016SACLX005 THÈSE DE DOCTORAT DE L’UNIVERSITÉ PARIS-SACLAY PRÉPARÉE À L’ÉCOLE POLYTECHNIQUE ÉCOLE DOCTORALE N°578 Sciences de l'homme et de la société Spécialité de doctorat : Sciences de Gestion et Epistémologie Appliquée Par Dr Idriss J. ABERKANE Mind Ergonomy for the Knowledge Economy. Software Neuroergonomics and Biomimetics for the Knowledge Economy Why? How? What? Thèse présentée et soutenue à Paris le 3 Février 2016 : Composition du Jury : Président : Prof. Francis Rousseaux Examinateur–IRCAM / URCA Dr. Paul Bourgine - Codirecteur Académique Unesco-Unitwin CSDC – Ecole polytechnique Prof. Pierre-Jean Benghozi - Codirecteur Académique Ecole polytechnique Dr. Samuel Tronçon - Codirecteur Industriel Groupe Résurgences Dr. Inès Safi – Examinateur - CNRS-Université Paris-Saclay Prof. -

Spring 2019 • Saturday, May 11
CommencementSpring 2019 • Saturday, May 11 UNIVERSITY OF WISCONSIN–MADISON UNIVERSITY OF WISCONSIN–MADISON CommencementONE HUNDRED AND SIXTY-SIXTH Law, Master’s, and Bachelor’s Degrees Saturday, May 11, 2019 12 p.m. Camp Randall Stadium Bascom Hall UNIVERSITY OF WISCONSIN–MADISON One Hundred and Sixty-Sixth Commencement Law, Master’s, and Bachelor’s Degrees Saturday, May 11, 2019 Wisconsin Welcome! Master of Professional French Studies Caroline Margaret Matkom, Master of Public Affairs Senior Class Vice President Master of Science BS, Community and Nonprofit Leadership ’19 Master of Social Work A Capella Performance by the MadHatters Dean William J. Karpus, PhD Processional Musical Interlude School of Music Band “Songs to Thee Wisconsin” Professor Michael Leckrone, MM School of Music Band Arranged by Professor Michael Leckrone, MM The audience is requested to rise Celebrating 150 Years of Women Receiving as the procession of officials enters. Degrees at UW National Anthem Cora Marrett, PhD Performed by Shaddai Solidum Remarks on Behalf of the Graduates MM, Vocal Performance ’19 Ronald Joseph Steinhoff, Senior Class President Welcome and Introduction of Official Party BA, Political Science and Spanish ’19 Provost Sarah C. Mangelsdorf, PhD Recognition of Graduates with Honors and Welcome from the Chancellor Distinction Chancellor Rebecca M. Blank, PhD Conferral of Baccalaureate Degrees Welcome from UW System Board of Regents Regent President John R. Behling, JD College of Agricultural and Life Sciences Bachelor of Science Charge to the Graduates Bachelor of Science–Agricultural Business Management J.J. Watt Bachelor of Science–Biological Systems Engineering Bachelor of Science–Dietetics Recognition of Honorary Degree Recipients Bachelor of Science–Landscape Architecture Honorary Degrees were awarded on Friday, May 10. -
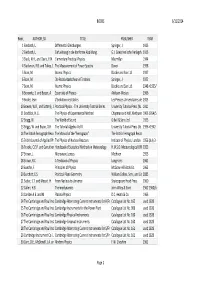
List of Books at 23 Oct 2014
BOOKS 6/11/2014 Book_ AUTHOR_SX TITLE PUBLISHER YEAR 1Bierbach, L. Differential Gleichungen. Springer, J. 1923 2Bierbach, L. Einfuehrung in die konforme Abbildung. G.J. Goeschen'sche Verlagsh 1915 3Black, N.H., and Davis, H.N. Elementary Practical Physics Macmillan 1944 4Blackman, R.B. and Tukey, J. The Measurement of Power Spectra Dover 1958 5Born, M. Atomic Physics Blackie and Son Ltd. 1937 6Born, M. Die Relativitaetstheorie Einsteins. Springer, J. 1922 7Born, M. Atomic Physics Blackie and Son Ltd. 1948 <1935/ 8Borowitz, S. and Beiser, A. Essentials of Physics Addison‐Wesley 1966 9Bosler, Jean. L'Evolution des Etoiles Les Presses Universitaires de 1923 10 Bowen, W.R., and Satterly, J. Practical Physics ‐ The University Tutorial Series University Tutorial Press (W. 1911 11 Braddick, H.J.J. The Physics of Experimental Method Chapman and Hall, Methuen 1966 1954/5 12 Bragg, W. The World of Sound G Bell & Sons Ltd 1923 13 Briggs, W. and Bryan, G.H. The Tutorial Algebra Vol II University Tutorial Press Ltd. 1956 <1942‐ 14 The British Ferrograph Reco The Manual of the "Ferrograph" The British Ferrograph Recor 15 British Journal of Applied Ph The Physics of Nuclear Reactors Institute of Physics, London 1956 (July 3‐ 16 Brooks, C.E.P. and Carruther Handbook of Statistical Methods in Meteorology H.M.S.O. Meteorological Offi 1953 17 Brown, J. Microwave Lenses Methuen 1953 18 Brown, R.C. A Textbook of Physics Longmans 1961 19 Bueche, F. Principles of Physics McGraw‐Hill Book Co. 1965 20 Burchett, E.S. Practical Plane Geometry William Collins, Sons, and Co 1885 21 Butler, S.T.