Towards Remote Monitoring of Sub-Seasonal Glacier Mass Balance
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Welttag Der Berge“ Am 11
Insta-Ranking zum „Welttag der Berge“ am 11. Dezember: Die beliebtesten Naturkolosse in Österreich und der Schweiz Rang Berg Instagram-Beiträge Höhe in Metern Staat(en) Gebirgsgruppe 1 Matterhorn 764.340 4478 Schweiz Italien Walliser Alpen 2 Monte Rosa: Grenzgipfel 206.977 4618 Schweiz Italien Walliser Alpen 3 Titlis 122.853 3238 Schweiz Urner Alpen 4 Großglockner 115.920 3798 Österreich Glocknergruppe 5 Kitzsteinhorn 112.705 3203 Österreich Glocknergruppe 6 Dents du Midi 34.577 3257 Schweiz Chablais-Alpen 7 Piz Buin 24.573 3312 Österreich Schweiz Silvretta 8 Breithorn 17.726 4164 Schweiz Italien Walliser Alpen 9 Weisshorn 16.090 4505 Schweiz Walliser Alpen 10 Wetterhorn 11.551 3692 Schweiz Berner Alpen 11 Mittagskogel 9.077 3162 Österreich Ötztaler Alpen 12 Wildspitze 8.396 3768 Österreich Ötztaler Alpen 13 Bouquetins 8.361 3838 Schweiz Italien Walliser Alpen 14 Piz Nair 7.722 3059 Schweiz Glarner Alpen 15 Piz Bernina 7.389 4049 Schweiz Bernina-Alpen 16 Piz Palü 7.176 3882 Schweiz Bernina-Alpen 17 Großvenediger 7.006 3657 Österreich Venedigergruppe 18 Klein Matterhorn 6.628 3883 Schweiz Walliser Alpen 19 Schreckhorn 5.503 4078 Schweiz Berner Alpen 20 Kranzberg 5.187 3742 Schweiz Berner Alpen 21 Bietschhorn 5.057 3934 Schweiz Berner Alpen 22 Allalinhorn 4.811 4027 Schweiz Walliser Alpen 23 Olperer 4.567 3476 Österreich Zillertaler Alpen 24 Schwarzhorn 4.556 3620 Schweiz Walliser Alpen 25 Schwarzhorn 4.556 3201 Schweiz Walliser Alpen 26 Schwarzhorn 4.556 3146 Schweiz Albula-Alpen 27 Schwarzhorn 4.556 3105 Schweiz Berner Alpen 28 Dufourspitze -

IFP 1707 Dent Blanche – Matterhorn – Monte Rosa
Inventaire fédéral des paysages, sites et monuments naturels d'importance nationale IFP IFP 1707 Dent Blanche – Matterhorn – Monte Rosa Canton Communes Surface Valais Evolène, Zermatt 26 951 ha Le Gornergletscher et le Grenzgletscher IFP 1707 Dent Blanche – Matterhorn – Monte Rosa Stellisee Hameau de Zmutt Dent Blanche avec glacier de Ferpècle 1 IFP 1707 Dent Blanche – Matterhorn – Monte Rosa 1 Justification de l’importance nationale 1.1 Région de haute montagne au caractère naturel et sauvage, avec nombreux sommets de plus de 4000 m d’altitude 1.2 Mont Rose, massif alpin avec le plus haut sommet de Suisse 1.3 Mont Cervin, montagne emblématique à forme pyramidale 1.4 Plusieurs glaciers de grande étendue avec marges proglaciaires intactes, en particulier le Gornergletscher, l’un des plus grands systèmes glaciaires de Suisse 1.5 Marmites glaciaires, roches polies et stries glaciaires, structures représentatives des diverses formes glaciaires 1.6 Situation tectonique unique dans les Alpes suisses, superposant des unités tectoniques et des roches de provenances paléogéographiques très variées 1.7 Vastes forêts naturelles de mélèzes et d’aroles 1.8 Phénomènes glaciaires et stades morainiques remarquables et diversifiés 1.9 Zones riches en cours d’eau et lacs d’altitude 1.10 Grande richesse floristique et faunistique, comprenant de nombreuses espèces rares et endémiques 1.11 Zmutt, hameau avec des bâtiments traditionnels bien conservés 2 Description 2.1 Caractère du paysage Le site Dent Blanche-Matterhorn-Monte Rosa est une zone de haute montagne encadrée de massifs montagneux imposants dans la partie méridionale du Valais et à la frontière avec l’Italie. -

Switzerland Welcome to Switzerland
Welcome to Switzerland A complete guide for your stay in Lausanne during the 15th CSCWD Conference Table of Contents I. Switzerland and the Lausanne region II. Access to Lausanne III. Restaurants in Lausanne IV. Transports in Lausanne V. Useful Information VII. Your venue: The Olympic Museum VIII. Tourism Activities I. Switzerland and the Lausanne region By its central geographical location, Switzerland is an ideal international destination for business, incentive and leisure travel. It is a country with many different facets. It unites an impressive variety of landscapes in a small geographical area and benefits from an exceptional natural heritage. As an important centre for communication and transport between the countries of Northern and Southern Europe, it has a common frontier with Germany, France, Italy, and the Principality of Liechtenstein. The Alpine Arc, just a few kilometers away from Lausanne, features some of the finest mountain peaks like the Matterhorn, Mont Blanc or the Jungfrau, and spectacular passes: Grimsel, St Gotthard, Simplon and Great St Bernard. These natural assets are further enhanced by security and dependability, Swiss values par excellence . The second largest city on the shore of Lake Geneva, Lausanne combines the dynamics of a business town with its ideal location as a holiday resort. Sport and culture are a golden rule in this Olympic capital. Nature, historic town, contemporary architecture, and exceptional surroundings: the Olympic capital is a model of the art of living and of cultural events. No need to wear out your shoes to visit the town and its region. A dense public transport network gives you the freedom to go from the lakeside to the trendy neighborhoods within minutes. -
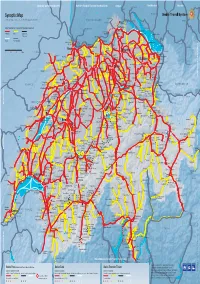
Synoptic Map + Beggingen + Due to Lack of Space, Not All Lines Are Indicated.Subject to Alterations
Strasbourg | Luxembourg | Bruxelles Karlsruhe | Frankfurt | Dortmund | Hamburg | Berlin Stuttgart Ulm | München München + + Stockach Engen Ravensburg Synoptic Map + Beggingen + Due to lack of space, not all lines are indicated.Subject to alterations. DEUTSCHLAND + + + Radolfzell Kempten + Singen + + Schleitheim Mulhouse Thayngen Insel +Mainau Swiss Travel System's network of trains, buses and boats + Schaffhausen + Meersburg + Zell (Wiesental) + + + + Neuhausen +Konstanz Erzingen + +Stein a.R. + + Railways Buses Cable cars, (Baden) +Rheinau Kreuzlingen + Friedrichshafen Funiculars Belfort + Marthalen Waldshut + + + + Weil a.R. + + + Boats No reductions + Koblenz + Zurzach + EuroAirport Riehen + Romanshorn + + + Frauenfeld Weinfelden + Immenstadt St-Louis +Basel Bad Bf Möhlin + + Laufenburg + Eglisau + + Rheinfelden + Lindau + Stein-Säckingen +Sonthofen Bülach Sulgen Nieder- + + Arbon + Basel + Pratteln +weningen Winterthur + +Frick + Bregenz 0102030km Montbéliard + Rorschach Turgi + Boncourt + + Bischofszell + Brugg + + + Liestal + Baden Rheineck + Oberglatt +Bonfol Dornach + +Wil + + + Gelterkinden + + St.Margrethen Rodersdorf + + Wettingen + Aesch + Zürich Heiden Sissach +Turbenthal St.Gallen Walzenhausen Roggenburg Flughafen + + + + + + + + Laufen Wildegg + Dornbirn Porrentruy + + Mellingen Effretikon + + +Dietikon Heerbrugg + Breitenbach Bazenheid Gossau + Trogen Oberstdorf + Aarau + + + + + Zürich Herisau Gais Altstätten Reigoldswil +Bauma + Waldenburg + Lenzburg Uitikon + + Delémont + Suhr + + Uster Damvant Olten + Wohlen+ Uetliberg -
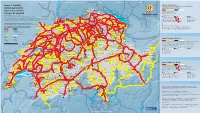
Swiss Pass Validity
Strasbourg | Paris | Luxembourg | Bruxelles Karlsruhe | Frankfurt | Dortmund | Hamburg | Berlin Stuttgart Ulm | München München Area of validity Stockach Swiss Travel Pass Swiss Travel Pass Youth | Swiss Travel Pass Flex | Swiss Travel Pass Flex Youth Geltungsbereich Ravensburg Beggingen Singen DEUTSCHLAND Thayngen Radolfzell Insel Lines for unlimited travel Rayon de validité Mulhouse Schleitheim Mainau Schaffhausen Meersburg Linien für unbegrenzte Fahrten Zell (Wiesental) Lignes avec utilisation illimitée Campo di validità Neuhausen Stein a.R. Konstanz Erzingen Linee per corse illimitate Version/Stand/Etat/Stato: 10. 2014 (Baden) Rheinau Kreuzlingen Friedrichshafen Waldshut Due to lack of space not all lines are indicated. Subject to change. Marthalen Basel Weil a. R. Aus Platzgründen sind nicht alle Linien angegeben. Änderungen vorbehalten. Bad Zurzach Weinfelden Lines with reductions (50%, 1 25%) No reductions EuroAirport Riehen Koblenz Eglisau Frauenfeld Romanshorn Lindau Pour des raisons de place, toutes les lignes ne sont pas indiquées. Sous réserve de modifications. Basel St. Johann Basel Möhlin Laufenburg Immenstadt Linien mit Vergünstigungen (50%, 1 25%) Keine Ermässigung Bad Bf Nieder- Lignes avec réductions (50%, 1 25%) Aucune réduction Per motivi di spazio, non tutte le linee sono presenti. Con riserva di modifiche. R’felden Stein-Säckingen Bülach Sulgen Arbon Basel weningen Sonthofen Linee che prevedono sconti (50%, 1 25%) Nessuno sconto Delle Pratteln Turgi Rorschach Bregenz Boncourt Ettingen Frick Brugg Bischofszell Rheineck -

GENUSS-WANDERUNGEN UM ZERMATT UND MATTERHORN – OPTION BREITHORN, 4164 M Neu 2022: Programm Jetzt 8 Tage Mit Wanderalternative Zur Breithorntour
Genuss-Touren / Wanderungen mit festem Stützpunkt / Europa / Schweiz / Wallis GENUSS-WANDERUNGEN UM ZERMATT UND MATTERHORN – OPTION BREITHORN, 4164 M Neu 2022: Programm jetzt 8 Tage mit Wanderalternative zur Breithorntour Beschreibung Wallis, Zermatt–Furi Höchster Wanderberg Europas: Oberrothorn, 3415 m Traumhafte Sicht vom Gornergrat und Fahrt mit der zweithöchsten Bergbahn in Europa Mit Matterhorn-Blick über den Europaweg Drei-Sterne-Hotel Silvana – das Summit Basecamp am Fuße des Matterhorns Option: Viertausenderbesteigung Breithorn, 4164 m (Teilnehmer: 4 – 6 Personen) Programm Zermatt ist immer eine Reise wert und das Matterhorn muss man einfach mal gesehen haben! Doch so einzigartig das Matterhorn ist, so beeindruckend ist die gigantische Viertausenderkulisse um das Bergsteigerdorf Zermatt. Dieser Ort ist nicht nur ein Mekka für Bergsteiger, sondern auch Anziehungspunkt für Touristen aus aller Welt. Entsprechend belebt geht es in dem autofreien Zermatt zu. Ganz bewusst haben wir das Drei-Sterne-Hotel Silvana im Weiler Furi gewählt. Wer Lust auf Trubel hat, kann Zermatt gut erreichen, alle anderen genießen die Ruhe am Hotel, wo mit einem schönem Wellnessbereich und einem Erlebnishallenbad für Abwechslung gesorgt ist. Weiterer Pluspunkt dieses Hauses ist das hervorragende Essen. Fünf bis sieben Stunden Gehzeit täglich sind geplant. Einige Wander- Highlights: Oberrothorn, 3415 m, einer der höchsten Wandergipfel Europas, sowie Gornergrat, 3090 m, beeindruckender Aussichtspunkt mit Blick auf die Monte-Rosa-Gruppe und viele weitere Viertausender. Im Lauf der Woche haben Sie zudem die Möglichkeit, selbst einen zu besteigen: Das Breithorn mit 4164 Metern. Erläuterungen: Gz 5 h Die Gehzeit ohne Pausen beträgt fünf Stunden. Hm ↑ 100 ↓ 200 Höhenmeter im Aufstieg bzw. im Abstieg. 1. Tag: Begrüßung um 16 Uhr am Bahnhof Zermatt beim Tourist Office durch Ihren Bergwanderführer Sie übergeben Ihr Gepäck für den Transport ins Hotel Silvana, 1900 m, gemeinsame Auahrt mit der Seilbahn zu dem kleinen Weiler Furi oberhalb von Zermatt. -

Postausgabe 04 | 2011
POST Ausgabe 04 | 2011 Inhaltsverzeichnis Clubvorschau 1 Editorial /Vorschau 2 Tourenberichte, Biblioth., Gesucht 2-4 Aus alten Zeiten / Homepage 5 Mitglieder 6 Hütten im Bergell 6-7 Jugend 8 Senioren 9-10 Live aus 10-11 Service 12 Impressum Redaktion/Druck/Versand: Coni Burri, Fredy Rähle Lektorat: Coni Burri, Fredy Rähle Layout: idfx AG Werbeagentur ASW Beiträge an [email protected] Redaktionsschluss: 24. Februar 2012 Clubvorschau Leckerbissen aus dem Sektionsprogramm Nachfolgend bei der Redaktion Wildspitz, 1580 m. TL Claude Andres TL: Willi Streuli, hier geht es direkt zur eingegangene Touren. Im Faltbüchlein startet diese leichte Senioren-Skitour in Bettenreservation der Wunschnächte: oder auf www.sachoherrohn.ch kann Ecce Homo (nicht in Griechenland) auf http://www.doodle.com/rwcxz4hw5z85 das vollständige Programm mit weiteren 731 m. Geeignet für alle Höhröhn- 58zs Informationen zu den Touren lerInnen. Wer kommt mit? TL: Claude nachgelesen werden. Andres, Tel: 044 780 27 78, [email protected] 23. Januar 2012 Stelli 2052 m Ab 1. Januar Jokertour Stelli wird eine leichte Tour im Aufstieg. Durchführungsdatum und Ziel offen: Für die Abfahrt braucht es etwas Im Winter herrschen oft während Tagen 7. Januar 2012 St. Antönien Kondition. Unbedingt vor der Meldefrist sehr günstige Lawinenverhältnisse Ebenfalls zum Saisonstart die passende anmelden. Sollte kein Schnee bis ins Tal (Stufe gering). Das ist die Zeit der leichte Tour in der Umgebung von St. liegen, wird diese Tour verlegt oder steilen, frechen Skitouren, die nur Antönien. Ca. 2-3 Std. Aufstieg. Wir verschoben! selten machbar sind. Genau dann findet reisen mit ÖV an, max. 8 Teilnehmer. TL: Willi Streuli, Tel: 071 787 40 90, die Joker-Tour statt. -

Wallis Dit Is De Bergwereld Ten Top: Hoog Boven Het Rhône-Dal Sluiten
Dit is de bergwereld Wallis ten top: hoog boven het Rhône-dal sluiten bergen van meer dan vierdui- zend meter hoogte Wallis van de buiten- wereld af. Uitgestrekte gletsjers stromen traag naar beneden, onderaan uitlopend op bruisende bergbeken die van de Rhône een steeds grotere rivier maken. Arvenbossen, alpenweiden en dorpen met donkerhouten huizen bovenin; abrikozen, wijnbouw en steden in het brede dal. Bij de uitmonding van de Rhône het zonnig blauwe Meer van Genève. Brig (HS) 218 Inleiding Inleiding STREEKKAART STREEKKAART 220 221 Inleiding West-Wallis In het hart van de Alpen ligt Wallis met in het brede dal de Rhône. karakter ontwikkeld. Het Lötschbergtal, pas na 1950 ontsloten, houdt Deze ontspringt uit de hoog gelegen Rhônegletsjer in het oosten, zijn eeuwenoude tradities in ere. Overal in Wallis staan grote houten tussen de Grimselpas en de Furkapas, en mondt uit in het Meer van boerenhuizen, prachtig donker getaand en van respectabele leeftijd. Genève. Het Rhônedal ligt ingesloten tussen machtige bergtoppen Een groot net van wandelwegen – bijna altijd in aansluiting op van veelal meer dan 4000 m hoogte: aan de noordflank Jungfrau trein of postauto – brengt de wandelaar in mooie dorpen als Ernen en Finsteraarhorn, in het zuiden Monte Rosa en Dufourspitze, Mat- en Grimentz, op bergweiden met een uitbundige bloemenpracht in terhorn en Dom. juni en juli, zelfs tot aan gletsjers. De Aletschgletsjer is de grootste, Voor wie uit het noorden komt is Wallis, door die machtige bergrug- langste en dikste van de hele Alpen. gen, alleen maar in het oosten, via de Furkapas of –tunnel, of in het westen, vanaf het Meer van Genève, toegankelijk. -

Gornergrat 3089 M Vrcholový Bod Vaší Cesty Ledovcovým Expresem
Švýcarsko vlakem, autobusem a lodí. Vydání 2011 Gornergrat 3089 m Vrcholový bod vaší cesty Ledovcovým expresem Zažijte špičkový přírodní ráj se všemi výhodami: – hora s panoramatickým výhledem na 29 čtyřtisícovek – celoro čně přístupná vyhlídková terasa – «Gornergrat Shopping» v hotelu 3100 Kulmhotel Gornergrat – nesčetné možnosti pěších túr Swiss Pass a Swiss Flexi Pass: Cesta zdarma do Zermattu, 50% sleva na cestu na Gornergrat Swiss Card: 50% sleva na cestu do Zermattu a na Gornergrat Bahnhofplatz 7 | CH-3900 Brig T +41 (0)27 921 41 11 | F +41 (0)27 921 41 19 www.gornergrat.ch | [email protected] 2 A5_STS_09_d.indd 1 25.09.09 10:00 Tak takhle se cestuje ve švýcarském stylu: Do vlaku nasednete kdy- koli si budete přát, třeba už na letišti. Pak si můžete vybrat au- tobus nebo vlak, podle toho kam míříte. Pokud se chcete pro- jet po jezeře, nasednete na loď. A jestli jedete do hor, na- stoupíte nesjpíše do ma- lého červeného vláčku. Celý systém, který fun- guje jako švýcarské ho- dinky. A tolik míst, která čeka- jí na objevení, v této krás- né malé zemi! To je Swiss Travel Sys- tem. Vše v jednom. S je- dinou jízdenkou. 3 Cestování. Užívat si vlak za vlakem. V síti InterCity a InterCity-Neigezug (IC a ICN) cestu- jete v klimatizovaných vagónech. Pokud je v jízdním řádu , zve vás na jídlo a nápoje jídelní vůz, naproti tomu označuje pojízdný minibar. V mnoha IC vla- cích jezdí dokonce hrací vagón pro naše nejmenší, tzv. rodinný vůz, označený FA. Na konci roku 2012 budou všechny dvoupodlažní vlaky IC vybaveny no- vým rodinným vozem Ticki Park. -

PERMAFROST Seventh International Conference June 23-27, 1998
PERMAFROST Seventh International Conference June 23-27, 1998 Program, Abstracts, Reports of the International Permafrost Association Yellowknife, Canada Editors: Antoni G. Lewkowicz Michel Allard Acknowledgments We are grateful to Shawne Clarke and Steve Kokelj, University of Ottawa and Laurent Desrochers and Caroline Lavoie, Universite Laval, for their hard work through the various stages of the production of this volume. iv The 7th International Permafrost Conference Preface This volume comprises the Conference Program, short abstracts, extended abstracts and reports of the International Permafrost Association. The technical portion of the Conference Program includes two Plenary sessions, two extensive Poster sessions and 22 Oral sessions. To fit all of these activities into the time available, three concurrent sessions were necessary for much of the conference. The 59 extended abstracts were submitted by graduate students and other authors whowished to present posters at the Conference and publish a summary of their research endeavours. These extended abstracts were edited but not reviewed. Both the short and extended abstracts are organized alphabetically in this volume by senior author. The reports of the Secretary General and the Working Groups of the International Permafrost Association, found in the last part of this volume, cover the period since the Sixth International Permafrost Conference in Beijing. The latter were prepared by various members of the Working Groups and describe meetings organized, publications produced, international collaboration and plans for the future. Some of these Working Groups will be renewed in Yellowknife while others have completed the tasks for which they were created. All Working Groups will report orally at the second plenary session. -

Meine Gipfelsammlung
Meine Gipfelsammlung Diese Liste ist gewidmet : Engelbert Treitinger, meinem (Ein)F¨uhrer in den Ostalpen, und Fred Fr¨olicher, meinem (Ein)F¨uhrer in den Westalpen. Ganz im Osten 1. Rangitoto 291m (Vulkan im Hafen von Auckland, mit Schiff und durch den Bush, nebst Bad im winterlichen South-Pacific, New Zealand 1973, wieder 1998) 2. Wytakeries 0m (mit David Gault, New Zealand, hier ging man umgekehrt : durch Bush und Schluchten zum Meer hinunter, daher die Null; mein “niedrigster” Gipfel) 3. Jiao Shan 300m (The Great Wall, Shan Hai Guan, China) 4. Tai Shan 1534m (der heilige Berg, Shandong Province, China) Dolmonites und Italien 5. Rosskopf 2600m (Obstanserseeh¨utte mit Beate) 6. Pfannspitze 2678m (Obstanserseeh¨utte mit Beate) 7. Zwolferkofel¨ 3094m (in den Sextenern mit Norbert) 8. Grosse Zinne 3003m (H. Frenademetz) 9. Plose 2571m (Brixen, allein) 10. Peitlerkofel 2875m (allein) 11. Saas Rigais 3025m (Reitberger) 12. Poppekanzel 2460m (Myriam) 13. Monte Maggiore 2200 m (Luggi) 14. Monte Pizzocolo 1581m (Lago di Garda, Luggi) 15. Gran Paradiso 4061m (Myriam, Andreas) 16. Vesuvio 1277m (Myriam) 17. Stromboli 924m (vom Meer aus; Myriam) Karwendel, Kette 1 18. Pfeiser Spitze 2317m (H. Atz) 19. Thaurer Jochspitze 2306m (H. Atz) 20. Rumer Spitze 2454m (H. Atz) 21. Gleirschtaler Brandjoch 2372m (H. Atz) 22. Brandjochkreuz 2268m (allein) 23. Vord. Brandjoch 2589m (Ernst, Alexander) 24. Hint. Brandjoch 2599m (Ernst 1971) 25. Hohe Warte 2596m (idem) 26. Kleiner Solstein 2637m (idem) 27. Grosser Solstein 2541m (idem) 28. Erlspitze 2405m (Engelbert+Inge, ⇒ Kuhljsp., Freiung, Seefeld) 29. Kreuzjochl¨ 2048m (Engelbert, Lisi) 30. Kuhljochspitze 2297m (oft) 31. Kuhljochscharte 2100m (h¨aufige Schitour, Engelbert, Norbert) 32. -

Höhenweg Rund Um ZERMATT Mit Bilderx
Höhenweg rund um ZERMATT 1. Tag: Sonntag 21.07.2013 Am Sonntag haben wir uns um 14 Uhr am Bahnhof in Täsch im Mattertal getroffen. Jonas unser Bergführer vom Alpin Center Oase hat uns herzlich begrüßt. Unsere Gruppe bestand aus neun Frauen und zwei Männern im Alter zwischen 32 Jahren und 60 Jahren. Da eine Teilnehmerin etwas zu spät kam, konnten wir erst um 14 Uhr 45 starten. Der Aufstieg zur Täschalp begann gleich richtig steil. Bei der kleinen Kirche am Täschberg mussten wir unsere Regenbekleidung anziehen, da ein kurzer Schauer niederging. Nach ca. einer viertel Stunde konnten wir diese wieder in den Ruck- sack stecken und sind dann bei schwülen Wetter weiter über Eggenstadel nach Ottavan. Dort befindet sich die Täschalp (2.214m) . Von hier hat man einen herrlichen Blick auf den Dom und den Alphubel. Wir wurden von der Hüttenwirtin herzlich begrüßt. Hier hatten wir für die erste Nacht ein gemeinsames Lager. Wer wollte konnte für 6 Franken duschen. Um 18 Uhr gab es Abendessen, dieses hat uns sehr gut geschmeckt. Hüttenruhe wie üblich 22 Uhr. 2. Tag: Montag 22.07.2013 Gut ausgeruht und gestärkt sind wir um 7 Uhr 35 gestartet über den neu erbauten Europaweg. Dies ist ein sehr schöner Höhenwanderweg mit ständigem Blick ins Mattertal. Täsch und Zermatt konnten wir im Tal gut erkennen, außerdem hatten wir einen großartigen Blick aufs Matterhorn. Etwas verwöhnt vom Höhenweg begann der steile Aufstieg über das Ritzengrat zum Unterrothorn (3.103m). Dort angekommen hatten wir einen herrlichen Blick auf die Schweizer Alpen. Nach einer kleinen Rast, begann der Abstieg zur Fluhalphütte (2.618 m).Ein Teil der Gruppe wollte noch gerne das Oberrothorn (3.414 m) besteigen ( dies ist der höchste Wanderberg Europas), der Aufstieg musste ab er wegen schlechtem Wetter abgebrochen werden.