Design of a Small Aqueous Homogeneous Reactor for Production of 99Mo Improving the Reliability of the Supply Chain
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Extraction Processing of Concentrated Solutions of Uranyl Nitrate with High Impurities Content V.M
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Electronic archive of Tomsk Polytechnic University Сhemistry UDC 546.791.02.238:66.061.51 EXTRACTION PROCESSING OF CONCENTRATED SOLUTIONS OF URANYL NITRATE WITH HIGH IMPURITIES CONTENT V.M. Korotkevich, V.V.Lazarchuck, T.G. Shikerun, V.I. Shamin, N.A. Mikhailova, F.A. Dorda Federal Unitary Enterprise Siberian Group of Chemical Enterprises, Seversk Еmail: [email protected] Process flowsheet of recycling uranium concentrated solutions with its purification from insoluble impurities of iron, silicon, molybde num, calcium oxides and hydroxides and soluble impurities with application of centrifugal extractors cascade has been developed and suggested for commercial introduction. The process was carried out at extractant saturation (30 % tributyl phosphate in hydrocarbon diluent) in extraction assembly lower than a limiting level (85...95 g/l) and in wash assembly – at limiting saturation (up to 120 g/l). As a result the waste uranium content in watertail solutions 0,01...0,04 g/l and minimal content of impurities in reextractors is provided. Perspective program on development of nuclear technology are also: reliability of hermetization, possi power engineering proposes to involve wide range of raw bility of remote service, resistance to corrosive attack of materials from uranium ores to secondary uranium ma structural materials, duration of overhaul period etc. terials into processing at atomic enterprises. In this case In Russia the centrifugal extractor of ECТseries the problem of reprocessing concentrated uranium so with continuous extraction of solid phase [3], which may lutions with high impurity content occurs. -
Nitrate (UO2 (NO)) 4
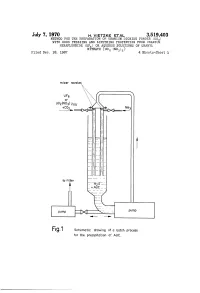
July 7, 1970 H. VETZKE ETA 3,519,403 METHOD FOR THE PREPARATION OF URANIUM DIOXIDE POWDER (UO) WITH GOOD PRESSING AND SINTERING PROPERTIES FROM URANIUM HEXAFLUORIDE (UF) OR AQUEOUS SOLUTIONS OF URANYL Fied Dec. 18, 1967 NiTRATE (UO2 (NO)) 4. Sheets-Sheet l mixer nozzles --race to fitter Fig.1 Schematic drawing of a batch process for the precipitation of AUC. July 7, 1970 H. VETZKE EA 3,519,403 METHOD FOR THE PREPARATION OF URANIUM DIOXIDE POWDER (UO) WITH GOOD PRESSING AND SINTERING PROPERTIES FROM RANIUM HEXAFLUORIDE (UF) OR AQUEOUS SOLUTIONS OF URANYL Filed Dec. 8, 1967 NiTRATE (UO2 (NO)) 4. Sheets-Sheet 3. mixer nozzles UF6 Of U02 (NO3)2ad tC92--X Ex-Ns / to filter cooling precipitation Vessel vessel Fig. 2 Schematic drawing of a continuous process for the precipitation of AUC July 7, 1970 H, VETZKE ETAL 3,519,403 METHOD FOR THE PREPARATION OF URANIUM DIOXIDE POWDER (UO) WITH GOOD PRESSING AND SINTERING PROPERTIES FROM URANIUM HEXAFLUORIDE (UF) OR AQUEOUS SOLUTIONS OF URANYL Filed Dec. 18, 1967 NiTRATE (UO (NO)2) 4. Sheets-Sheet 3 Off gas Off gas 487\m Nx UO2 powder XXX.& X.X S& steam / H2 Fig. 3 Ot Schematic drawing of a fluidized bed furnace for the reduction of AUC to U02, July 7, 1970 H. VEZKE ETAL 3,519,403 METHOD FOR THE PREPARATION OF URANIUM DIOXIDE POWDER (UO) WITH GOOD PRESSING AND SINTERING PROPERTIES FROM URANIUM HEXAFLUORIDE (UF) OR AQUEOUS SOLUTIONS OF URANYL NITRATE (UO2 (NO)a) Filed Dec. 18, 1967 4. Sheets-Sheet 1 -- Offgas Step 1: Decomposition, reduction and pyrohydrolysis i Step 2: Pyrohydrolysis Step 3: Controlled oxidation an o- are as an un- Fig. -

Used As a Reference in Ou 1 Ri)
6307 U-003-307 .8 SUMMARY TECHNICAL REPORT FOR THE PERIOD APRIL 1, 1959 TO JUNE 30, 1959 - (USED AS A REFERENCE IN OU 1 RI) 07/20/59 NLCO-790 NLO 75 REPORT SUMMARY TECHNICAL REPORT I. For t le Period April 1, 1959 to June 30, 1959 I I AEC RESEARCH AND DEVELOPMENT REPORT NLCO- 790 -w6307 Technology -Feed Materials ..:i (M- 3679, 22nd Ed.) 8 - SUMMARY TECHNICAL REPORT FOR THE PERIOD - APRIL 1, 1959 TO JUNE 30, 1959 F. L. CUTHBERT, DIRECTOR c. E. CROMPTON, ASSOCIATE DIRECTOR TECHNICAL DIVISION ._. EDITED BY JOHN W. SIMMONS Date of Issuance: July 20, 1959 NATIONAL LEAD COMPANY OF OHIO p ' I Box 158, Cincinnati 39, Ohio *I Contract No. AT(30 -1) -1156 "630'7 -3- Page No. .' - .. SUMMARY. .. '. 7 - Feed Materials Evaluation :...I '. 11 I. .- . .. 2. Selective Digestion . :-;. 17 ,>+ 3. Bondingin theTri-n-butylPhosphate-H20-U-AcidSy$tem . 27 4. Extraction Column Control . ..: . 37 5. Activation of Pot-Produced Orange Oxide . .' . 41 . Hydrofluorination of Sodium-ContamGated Uranium Oxides. 41 Thermal Decomposition of AnhydibusUranylSulfate . 44 i .. 6. ADU ("Ammonium Diuranate") Process Development . 49 . Laboratory Determination of Impurity Decontamination by an ADU Process . 49 '- Thermobalance Hydrofluorination Investigation of Pilot Plant ADU . 52 7. Analyses of Variations in Visually Determined Derby Grades . 57 8. Recovery of Uranium from a Mixture of Uranium, Magnesium, and Magnesium Fluoride . 61 9. Scrap Processing by an Aqueous UF4 Process . 67 Labomtory Preparation of Green Salt from Plant-Produced UAP and Black Oxide . 67 Green Salt Preparation from Pickle Liquor, Black Oxide, and Reduction Pot Residues . 71 io. -

United States Pmao" ICC Patented June 30, '1959 1 2 Adsorption on Manganese Dioxide, but It May on the 2,892,677 Other Hand He Left in the Solution
r. 2,892,677 United States Pmao" ICC Patented June 30, '1959 1 2 adsorption on manganese dioxide, but it may on the 2,892,677 other hand he left in the solution. If it is removed, a certain amount of manganese nitrate is formed from the ' SEPARATION OF URANIUM FROM THORIUM manganese dioxide in the solution and this nitrate reacts AND PROTACTINIUM with the sodium diethyldithiocarbamate to give manga William Kenneth Rodgerson Musgrave, Durham, Eng ' nese diethyldithiocarbamate, which must subsequently be land, assignor, by mesne assignments, to the United separated from the uranium. ,, . .States of America as represented by the United States Whether or not the protactinium has been removed, Atomic Energy Commission the solution is brought to a pH of between 2 and 3, for No Drawing. Application November 27, 1946 10 example by the addition of ammonia. The sodium di Serial No. 712,722 ethyldithiocarbamate is then dissolved in a solvent in which the subsequently formed uranyl diethyldithiocar '8 Claims. (Cl. 23—14.5) bamate is also soluble. Such a solvent is, for example, amyl acetate or methyl isobutyl ketone, the former being This invention relates to the separation of uranium 15 preferable for the reasons which will be indicated below. from thorium and protactinium. A mixture of these The sodium diethyldithiocarbamate is dissolved in amyl elements is obtained, for example, as the result of irradia acetate to form a solution containing 0.25% of the tion by neutrons of so-called thorium carbonate, which former, and this solution is then shaken up with the is a mixture of thorium oxide and thorium carbonate. -

Solvent Extraction of Uranium with Acetylacetone and Tri-N-Butyl
DAEHAN HWAHAK HWOEJEE (Journal of the Korean Chemical Society) Vol. 24, No. 3, 1980 Printed in the Republic of Korea 아세 틸아세톤과 트리부틸인산의 도데칸용액 에 의한 우라늄의 용매추출 裴奎善-鄰奇碩 韓國核燃料開發公團 (1980. 2. 27 接受 ) Solvent Extraction of Uranium with Acetylacetone and Tri-n-Butyl Phosphate in “-Dodecane Kyu Sun Bai and Key Suck Jung Korea Nuclear Fuel Development Institute, Daeduck 300-32, Korea (Received Feb. 27, 1980) 요 악 . 도데칸에 녹인 아세틸아세톤과 트리부틸인산으로 묽은 질산우라닐수용액에서 우라늄 (VI) 을 추출했다 . pHl 이상에서 이 혼합추출제의 상승적 효과가 관측되었다 . 추출되는 화학종은 1:2:1 및 1:2:2 우라닐 -아세털 아세톤 -트리부털 인산착물이다 . 이들 반응의 추출정수들을 측정하였다 . ABSTRACT. Uranium (VI) was extracted from dilute aqueous solutions of uranyl nitrate with acetylacetone and tri-n-butyl phosphate in n-dodecane. Synergistic effect was observed with the mixed reagents above pH 1, The species extracted are the 1:2:1 and the 1:2:2 uranyl-AA-TBP complexes. The extraction constants for these reactions have been determined. by crystallization of the salt as UO2(NO3)2 INTRODUCTION •6H2O. HAA and TBP were dissolved in do Acetylacetone (HAA) is a simple -diketone. decane and uranyl nitrate in water. Equal A weak acid with pKa=8. 2% HAA has long volumes of organic and aqueous phases were been used as a chelating agent for many equilibrated in 100 mZ separatory funnels by metals.2 It is quite soluble in water and its vigorous shaking for several minutes. Equili brium temperature was 25 °C or ambient. pH distribution coefficient is E=5. 95 for benzene/ water system.3 Because of its solubility in measurements were made by using a Corning water, HAA has not been so widely used as, Model 130 pH meter. -

Spectroscopic Signatures of Uranium Speciation for Forensics
UNLV Theses, Dissertations, Professional Papers, and Capstones May 2017 Spectroscopic Signatures of Uranium Speciation for Forensics Nicholas Wozniak University of Nevada, Las Vegas Follow this and additional works at: https://digitalscholarship.unlv.edu/thesesdissertations Part of the Chemistry Commons Repository Citation Wozniak, Nicholas, "Spectroscopic Signatures of Uranium Speciation for Forensics" (2017). UNLV Theses, Dissertations, Professional Papers, and Capstones. 3063. http://dx.doi.org/10.34917/10986257 This Dissertation is protected by copyright and/or related rights. It has been brought to you by Digital Scholarship@UNLV with permission from the rights-holder(s). You are free to use this Dissertation in any way that is permitted by the copyright and related rights legislation that applies to your use. For other uses you need to obtain permission from the rights-holder(s) directly, unless additional rights are indicated by a Creative Commons license in the record and/or on the work itself. This Dissertation has been accepted for inclusion in UNLV Theses, Dissertations, Professional Papers, and Capstones by an authorized administrator of Digital Scholarship@UNLV. For more information, please contact [email protected]. SPECTROSCOPIC SIGNATURES OF URANIUM SPECIATION FOR FORENSICS By Nicholas Robert Wozniak Bachelors of Science – Chemistry Bachelors of Science – Physics Hope College 2012 A dissertation submitted in partial fulfillment of the requirements for the Doctor of Philosophy – Radiochemistry Department of Chemistry College of Sciences The Graduate College University of Nevada, Las Vegas May 2017 Dissertation Approval The Graduate College The University of Nevada, Las Vegas April 14, 2017 This dissertation prepared by Nicholas Robert Wozniak entitled Spectroscopic Signatures of Uranium Speciation for Forensics is approved in partial fulfillment of the requirements for the degree of Doctor of Philosophy – Radiochemistry Department of Chemistry Ken Czerwinski, Ph.D. -

Technology of Uranium Purification. Impurities Decontamination
TECHNOLOGY OF URANIUM PURIFICATION. IMPURITIES DECONTAMINATION FROM URANYL CHLORIDE BY EXTRACTION WITH TRI-n-OCTYLAMINE IN THE PRESENCE OF THIOUREA AS COMPLEXING LIGAND. AIcídio Abrão PUBLICAÇÃO IEA 458 DEZEMBRO/1976 CEQ 69 PUBL. I EA 45B OEZEMBRO/1976 CEQ 68 TECHNOLOGY OF URANIUM PURIFICATION. IMPURITIES DECONTAMINATION FROM URANYL CHLORIDE BY EXTRACTION WITH TRI-n-OCTYLAMINE IN THE PRESENCE OF THIOUREA AS COMPLEXING LIGAND. Alcidio Abrio CENTRO DE ENGENHARIA QUÍMICA (CEQ) INSTITUTO DE ENERGIA ATÔMICA SAO PAULO - BRASIL APHOVAOO PARA PUBLICAÇÃO EM NOVEMBRO/1976 CONSELHO DELIBERATIVO Eng? HMcio Modnto da Costa Eng? Ivano Humbert Marchesi Prof. Admar Cervellim Prof. Sérgio Matcarenhai de Oliveira Dr. Klaus Reinach Or. Roberto D'Utra Vai SUPERINTENDENTE Prof. Dr, Ròmulo Ribe/r.» Pierori INSTITUTO DE ENERGIA ATÔMICA Caixa Postal 11.049 (Pinheiros) Cidade Universitária "Armando de Sallei Oliveira" SAO PAULO - BRASIL NOTA Este trabalho foi confe-ido p«lo autor depois de composto e sua redação tt'i conforme o original, sem qualquer correçáo ou mudança. TECHNOLOGY OF URANIUM PURIFICATION. IMPURITIES DECONTAMINATION FROM URANYL CHLORIDE BY EXTRACTION WITH TRI-n-OCTYLAMINE IN THE PRESENCE OF THIOUREA AS COMPLEXING LIGAND- Alcidio Abrão ABSTRACT The extraction of jranyl chloride by trinoctyiamme ITOAI and in decontamination from several impurities v»,th the aid of thiourea is investigated The effect of thiourea as a complexing agsnt, giving rise to unextracted canonic species of several metallic ion and its consequence in the extraction of uranyl chlonde from hydrochloric acid with TOA benzene!x'lenel is described Also, the effect of an acidified thiourea solution for scrubbing the organic phase loaded with uranyl chloride is studied INTRODUCTION The long chain amines had shown to be excellent extractants for various inorganic rid organic acds, and for a great number of anionic metallic complexes Smith and Page'441 had indicated the association properties of high weight amines w.th acids. -

Material Safety Data Sheet
SAFETY DATA SHEET URANYL NITRATE SOLUTION SECTION 1: CHEMICAL PRODUCT & COMPANY IDENTIFICATION New Brunswick Laboratory U.S. Department of Energy 9800 South Cass Avenue Argonne, IL 60439 1-630-252-CRMS (2767) Emergency Phone Numbers: 1-630-252-6130 or 1-630-252-5731 Chemical Name: Uranyl Nitrate Solution, UO2(NO3)2 Other Identifiers: Certified Reference Material (CRM) standard or Safeguards Measurement Evaluation (SME) sample Use and Restrictions: This material is prepared for use as a standard or in inter-laboratory comparison programs at analytical laboratories, which routinely handle uranium and/or plutonium. NBL expects that recipients of their material are in compliance with 29 CFR 1910.1200(h) which requires employers to provide employees with effective information and training on hazardous chemicals in their work area. SECTION 2: HAZARDS IDENTIFICATION OSHA HAZARDS: Skin Corrosion/Irritation Category 1B. Serious Eye Damage/Irritation Category 1 TARGET ORGANS: Skin, Eyes, Kidneys. GHS Label elements, including precautionary statements Signal Word: DANGER Pictogram: Page 1 of 12 Hazard Statement(s) H314 Causes severe skin burns and eye damage H373 May cause damage to organs through prolonged or repeated exposure. H411 Toxic to aquatic life with long lasting effects. Precautionary statement(s) P260 Do not breathe dust/ fume/ gas/ mist/ vapors/ spray. P262 Do not get in eyes, on skin, or on clothing. P264 Wash skin thoroughly after handling. P273 Avoid release to the environment. P280 Wear protective gloves/protective clothing/eye protection/face protection P310 Immediately call a POISON CENTER or doctor/ physician if swallowed or inhaled. Other Hazard(s): Radioactive NFPA RATINGS (SCALE 0-4): Health=3 Fire=0 Reactivity=0 Special Hazard= OX SECTION 3: COMPOSITION/INFORMATION ON INGREDIENTS Chemical Name: Uranyl Nitrate Solution Common Names/Synonyms: CRM U045; CRM 135; CRM 145; CRM 145-B; CRM U930-D; Safeguards Measurement Evaluation (SME) Low Enrichment, Normal Enrichment, or High Enrichment Solutions; Uranyl Nitrate in Nitric Acid Solution. -

Uranyl Nitrate, 1%
Uranyl Nitrate, 1% 1. Identification Product Name: Uranyl Nitrate, 1% Item #: DI0103014, DI0103029, SKC1048-250, SKC1048-500 Web SDS: S231 Synonyms: N/A Recommended Use: Special Stains Restrictions on Use: N/A Manufacturer: In Case of Emergency: BBC Biochemical Chemtrec US 1-800-424-9300 409 Eleanor Lane, Chemtrec International 703-527-3887 Mount Vernon, WA 98273 1-800-635-4477 2. Hazards Identification OSHA Hazard Classification(s): Acute Toxicity - Oral - Category 4 Acute Toxicity - Inhalation - Category 4 Signal Word: Warning Hazard Statement(s): Harmful if swallowed. Harmful if inhaled. Pictogram(s): Precautionary Statement(s): Prevention: Wash body thoroughly after handling. Do not eat, drink or smoke when using this product. Avoid breathing dust, vapors. Use only outdoors or in a well-ventilated area. Response: If swallowed: Call a doctor if you feel unwell. Rinse mouth. If inhaled: Remove person to fresh air and keep comfortable for breathing. Call a doctor if you feel unwell. Storage: N/A Disposal: Dispose of contents/container in accordance with local regulations. Descriptions of Hazards not otherwise classified: N/A Percent of mixture with unknown acute toxicity: N/A 3. Composition and Information on Ingredients Chemical Name Common Name CAS # Concentration % Uranyl Nitrate 13520-83-7 1 Water 7732-18-5 99 4. First Aid Measures Eye Contact: If in eyes: Rinse cautiously with water for several minutes. Remove contact lenses, if present and easy to do. Continue rinsing. If eye irritation persists: Get medical advice/attention. Skin Contact: If on skin (or hair): Take off immediately all contaminated clothing and wash before reuse. -

Physcio-Chemical Studies on the Systems Uranyl Nitrate Organic Solvent
Durham E-Theses Physcio-chemical studies on the systems uranyl nitrate organic solvent - water Mathieson A. R., How to cite: Mathieson A. R., (1951) Physcio-chemical studies on the systems uranyl nitrate organic solvent - water, Durham theses, Durham University. Available at Durham E-Theses Online: http://etheses.dur.ac.uk/9766/ Use policy The full-text may be used and/or reproduced, and given to third parties in any format or medium, without prior permission or charge, for personal research or study, educational, or not-for-prot purposes provided that: • a full bibliographic reference is made to the original source • a link is made to the metadata record in Durham E-Theses • the full-text is not changed in any way The full-text must not be sold in any format or medium without the formal permission of the copyright holders. Please consult the full Durham E-Theses policy for further details. Academic Support Oce, Durham University, University Oce, Old Elvet, Durham DH1 3HP e-mail: [email protected] Tel: +44 0191 334 6107 http://etheses.dur.ac.uk PSYSIC0-CH3MICAL STUDIES OH THE SYSTEMS DEAUTL 1TITRATE - ORGANIC SOLVENT - WATER A.R. Mathieson, B.Sc.(Dunelm), A.R.I.C. Thesis presented for the degree of M. Sc. in Pure Science of the University of Durham, August 1951 The experimental work described in this thesis was performed at the Atomic Energy Research Establishment, Harwell, during the period November 1947 - December 1949* The results have already been published elsewhere: Mathieson "Stability of Complexes of Uranyl Nitrate with Ketones and Ethers", J. -

Analysis of Mo Production Capacity in Uranyl Nitrate Aqueous
A. Isnaeni,Atom atIndonesia al., / Atom Vol. Indonesia 40 No. 1 Vol.(2014) 40 40No. - 143 (2014) Analysis of 99Mo Production Capacity in Uranyl Nitrate Aqueous Homogeneous Reactor using ORIGEN and MCNP A. Isnaeni*, M.S. Aljohani, T.G. Aboalfaraj and S.I. Bhuiyan Nuclear Engineering Department, King Abdulaziz University P.O. Box 80240 Jeddah, Kingdom of Saudi Arabia A R T I C L E I N F O A B S T R A C T Article history: 99mTc is a very useful radioisotope in medical diagnostic procedure. 99mTc is Received 11 January 2014 produced from 99Mo decay. Currently, most of 99Mo is produced by irradiating 235U Received in revised form 18 February 2014 in the nuclear reactor. 99Mo mostly results from the fission reaction of 235U targets Accepted 28 February 2014 with a fission yield about 6.1%. A small additional amount is created from 98Mo 99 neutron activation. Actually Mo is also created in the reactor fuel, but usually we Keywords: 99 do not extract it. The fuel will become spent fuel which is a highly radioactive Mo waste. 99Mo production system in the aqueous homogeneous reactor offers a better Uranyl nitrate method, because all of the 99Mo can be extracted from the fuel solution. Fresh Homogeneous reactor reactor fuel solution consists of uranyl nitrate dissolved in water. There is no MCNP separation of target and fuel in an aqueous homogeneous reactor where target and ORIGEN fuel become one liquid solution, and there is no spent fuel generated from this reactor. Simulation of the extraction process is performed while reactor in operation (without reactor shutdown). -

Uranyl Nitrate Hazard Summary Identification
Common Name: URANYL NITRATE CAS Number: 10102-06-4 RTK Substance number: 1978 DOT Number: UN 2981 (Solid) Date: April 2000 ----------------------------------------------------------------------- ----------------------------------------------------------------------- HAZARD SUMMARY * Uranyl Nitrate can affect you when breathed in and may * If you think you are experiencing any work-related health be absorbed through the skin. problems, see a doctor trained to recognize occupational * Contact can irritate and burn the skin and eyes with diseases. Take this Fact Sheet with you. possible eye damage. * Breathing Uranyl Nitrate can irritate the nose, throat and WORKPLACE EXPOSURE LIMITS lungs causing coughing, wheezing and/or shortness of The following exposure limits are for soluble Uranium breath. compounds (measured as Uranium): * High exposures to Uranyl Nitrate can cause nausea, vomiting, muscle weakness, and convulsions. OSHA: The legal airborne permissible exposure limit * Uranyl Nitrate may damage the liver and kidneys. (PEL) is 0.05 mg/m3 averaged over an 8-hour * Repeated exposure to Uranyl Nitrate may affect the brain. workshift. * CONSULT THE NEW JERSEY DEPARTMENT OF HEALTH AND SENIOR SERVICES HAZARDOUS NIOSH: The recommended airborne exposure limit is SUBSTANCE FACT SHEET ON URANIUM. 0.05 mg/m3 averaged over a 10-hour workshift. IDENTIFICATION ACGIH: The recommended airborne exposure limit is Uranyl Nitrate is a pale yellow, radioactive solid with no 0.2 mg/m3 averaged over an 8-hour workshift odor. It is used in photographic processes, glazing ceramics, and 0.6 mg/m3 as a STEL (short term exposure and radiation shielding. limit). REASON FOR CITATION * The above exposure limits are for air levels only. When * Uranyl Nitrate is on the Hazardous Substance List skin contact also occurs, you may be overexposed, even because it is regulated by OSHA and cited by ACGIH, though air levels are less than the limits listed above.