The Design of a Metro Network Using a Genetic Algorithm
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Naylor Road Metro Station Area Accessibility Study
Naylor Road Metro Station Area Accessibility Study Pedestrian and Bicycle Metro Station Access Transportation Land-Use Connection (TLC) National Capital Region Transportation Planning Board Metropolitan Washington Council of Governments The Maryland-National Capital Park and Planning Commission May 2011 Introduction .................................................................................................................................................. 1 Recommendations ....................................................................................................................................................................... 2 Study Overview ............................................................................................................................................. 4 Study Process ............................................................................................................................................................................... 6 Background .................................................................................................................................................................................. 6 Planning Context and Past Studies ............................................................................................................................................... 7 Existing Conditions and Challenges ............................................................................................................. 10 Public Outreach ......................................................................................................................................................................... -

Pentagon City Metro Station Second Elevator Transportation Commission
Pentagon City Metro Station Second Elevator Transportation Commission July 01, 2021 Pentagon City Metro Station Second Elevator • BACKGROUND: The Pentagon City Metrorail station is one of the highest in terms of ridership among stations in Northern Virginia,. • Provides access to multiple retail, government, and commercial office buildings, and is a transfer point for regional and local transit buses and numerous private bus services. • Construction of a new second elevator Intersection of S Hayes and S 12th Streets on the north side of the passageway corresponds to the new second New Elevator Existing elevator being in the general area of Elevator the pedestrian path for people crossing S. Hayes Street. July 01, 2021 Pentagon City Metro Station Second Elevator Project Scope: • The second elevator will eliminate the need to cross six (6) lanes of traffic, two parking lanes, and a bike lane to reach the elevator on the east side of S. Hayes Street. • Improves ADA access and access for passengers with strollers and luggage. • Provide redundancy, in accordance with current WMATA design criteria, when one of the elevators is out of service for any reason. July 01, 2021 Pentagon City Metro Station Second Elevator Construction Phase: On January 25, 2021, Arlington County received two (2) bids • The low bidder, W.M. Schlosser Company, Inc. was awarded the contract on April 19, 2021 for $6.4 mil. • The County and Procon (CM), will work together with the Washington Metropolitan Area Transit Authority (WMATA) to ensure construction is performed -

Walking Toward Metro Stations: the Contribution of Distance, Attitudes, and Perceived Built Environment
sustainability Article Walking toward Metro Stations: the Contribution of Distance, Attitudes, and Perceived Built Environment Mohammad Paydar 1,* , Asal Kamani Fard 2 and Mohammad Mehdi Khaghani 3 1 Escuela de Arquitectura Temuco, Facultad de Humanidades, Universidad Mayor, Av. Alemania 281, Temuco 4780000, Chile 2 Academic Researcher, Universidad Católica del Maule, San Miguel 3605, Talca, Chile; [email protected] 3 Department of Urban Studies, Apadana Institute of Higher Education, Shiraz 7187985443, Iran; [email protected] * Correspondence: [email protected] Received: 17 September 2020; Accepted: 16 November 2020; Published: 9 December 2020 Abstract: Walking as an active means of travel is important as a sustainable mode of transport. Moreover, the level of walking in the surrounding areas of metro stations would contribute to maintaining the minimum rate of physical activity and, therefore, inhabitants’ general health. This study examined the impacts of walking attitude, walking distance, and perceived built environment on walking behavior for reaching the metro stations in Shiraz, Iran. Three metro stations were selected and a quantitative approach was used to examine the objectives. It was found that the average walking distance is less than the average in developed countries, such as the United States. People walked more when there was a shorter distance between their starting points and the metro stations. The contribution of walking attitudes and several built environment attributes to walking behavior was demonstrated. Finding the contribution of aesthetic attributes, such as accessibility to parks and housing types of the starting points of the walking trips, to walking for transport are taken into account as the novelties of this study. -

Turkey Business Guide
Turkey Business Guide Compiled by: Swiss Business Hub Turkey Istanbul, August 2018 ARRIVAL AND DEPARTURE Ordinary and official passport holders are exempted from visa for their travels up to 90 days. Visa is only valid when the purpose of travel is tourism or commerce. For other purposes, such as work and study, visas are given by Turkish Embassies or Consulates. To learn more about visa procedures, please visit www.mfa.gov.tr and contact the nearest Turkish Embassy or Consulate. For information about the customs’ regulations on entry and exit, please visit www.gtb.gov.tr. You can also refer to the Embassy web page to get information on various topics (www.eda.admin.ch/ankara). LANGUAGES USED FOR BUSINESS The official language is Turkish. In business, English is the preferred language for communication. In tourism, German and Russian are most commonly spoken foreign languages which are followed by French, Italian and Arabic. Translators are available at a cost from business service provider companies. Switzerland Global Enterprise – Business Guide 1/11 PUBLIC HOLIDAYS January 1 New Year holiday April 23 National Sovereignty and Children's Day May 19 Commemoration of Atatürk and Youth & Sports Day July 15 Democracy and National Unity Day August 30 Victory Day October 29 Republic Day Religious Holidays The dates of the religious festivals change according to the Muslim lunar calendar and thus occur 10 days earlier each year. − Ramadan or Seker Bayrami (the Festival of Fast-Breaking): 3-day festival. − Kurban Bayrami (the Festival of Sacrifice): 4-day festival. HEALTH AND INOCULATIONS Turkey does not pose any unusual health risks. -

DLA Piper. Details of the Member Entities of DLA Piper Are Available on the Website
EUROPEAN PPP REPORT 2009 ACKNOWLEDGEMENTS This Report has been published with particular thanks to: The EPEC Executive and in particular, Livia Dumitrescu, Goetz von Thadden, Mathieu Nemoz and Laura Potten. Those EPEC Members and EIB staff who commented on the country reports. Each of the contributors of a ‘View from a Country’. Line Markert and Mikkel Fritsch from Horten for assistance with the report on Denmark. Andrei Aganimov from Borenius & Kemppinen for assistance with the report on Finland. Maura Capoulas Santos and Alberto Galhardo Simões from Miranda Correia Amendoeira & Associados for assistance with the report on Portugal. Gustaf Reuterskiöld and Malin Cope from DLA Nordic for assistance with the report on Sweden. Infra-News for assistance generally and in particular with the project lists. All those members of DLA Piper who assisted with the preparation of the country reports and finally, Rosemary Bointon, Editor of the Report. Production of Report and Copyright This European PPP Report 2009 ( “Report”) has been produced and edited by DLA Piper*. DLA Piper acknowledges the contribution of the European PPP Expertise Centre (EPEC)** in the preparation of the Report. DLA Piper retains editorial responsibility for the Report. In contributing to the Report neither the European Investment Bank, EPEC, EPEC’s Members, nor any Contributor*** indicates or implies agreement with, or endorsement of, any part of the Report. This document is the copyright of DLA Piper and the Contributors. This document is confidential and personal to you. It is provided to you on the understanding that it is not to be re-used in any way, duplicated or distributed without the written consent of DLA Piper or the relevant Contributor. -
PLANNING GUIDE for Public Transportation Elevators Table of Contents
PLANNING GUIDE FOR Public transportation elevators Table of Contents 1. Introduction ...........................................................................................................4 1.1 About this Planning Guide ............................................................................................4 1.2 About KONE .................................................................................................................4 2. Special demands of public transportation ........................................................... 7 2.1 Airports ........................................................................................................................7 2.1.1 Benefits of KONE elevators for airports ...................................................................................... 7 2.2 Transit centers (railway and metro ststions) ...................................................................8 2.2.1 Benefits of KONE elevators in railway and metro stations .......................................................... 8 2.3 Main specifications for public transportation elevators ...............................................10 2.4 Electromagnetic compatibility standards ....................................................................11 2.5 LSH and LH cables ......................................................................................................11 3. Odering a public transportation elevator ...........................................................12 3.1 Key cost drivers for elevators in -

Shuttle Services at Metro Facilities August 2011
Shuttle Services at Metro Facilities August 2011 Shuttle Services at Metro Facilities Washington Metropolitan Area Transit Authority Office of Bus Planning August 2011 Washington Metropolitan Area Transit Authority Office of Bus Planning Jim Hamre, Director of Bus Planning Krys Ochia, Branch Manager 600 5th Street NW Washington, DC 20001 Parsons Brinckerhoff Brian Laverty, AICP, Project Manager Nicholas Schmidt, Task Manager 1401 K Street NW, Suite 701 Washington, DC 20005 Contents Executive Summary ES-1 Existing Conditions ES-1 Policies and Procedures ES-2 Future Demand ES-3 Recommendations ES-4 Introduction 1 Study Process 3 Coordination 3 On-Site Observations 3 Operating Issues 3 Future Demand 4 Permitting and Enforcement 4 Existing Conditions 7 Key Observations 8 Operating Issues 9 Policies and Procedures 17 Permitting 17 Enforcement 19 Future Demand 25 Methodology 25 Results 28 Recommendations 33 Facility Design 34 Demand Management 37 Permitting 39 Enforcement 42 Contents | i Figures Figure ES-1: Future Shuttle Demand Estimate ES-4 Figure 1: Location of Peer U.S. Transit Agencies 4 Figure 2: Study Stations 7 Figure 3: Vehicles in Tight Turning Areas May Block Bus Bay Entrances (New Carrollton Station) 11 Figure 4: Long Kiss & Ride Queue (New Carrollton Station) 11 Figure 5: Pedestrian Shortcut (Southern Avenue Station) 11 Figure 6: Shuttle Blocking Kiss & Ride Travel Lane (King Street Station) 12 Figure 7: Shuttle Blocking Bus Stop (Anacostia Station) 13 Figure 8: Typical Signs Prohibiting Non-Authorized Access to Station Bus Bays -

Detecting Illegal Pickups of Intercity Buses from Their GPS Traces *
2014 IEEE 17th International Conference on Intelligent Transportation Systems (ITSC) October 8-11, 2014. Qingdao, China Detecting Illegal Pickups of Intercity Buses from Their GPS Traces * Ling Yin, Jinxing Hu, Lian Huang, Fan Zhang, and Peng Ren Abstract—In some regions, especially in developing countries Therefore, this illegal pickup behavior has to be controlled and such as China and India, intercity bus drivers would like to pick stopped. Police Department in many cities of China put in a up passengers outside the scheduled bus stations and pocket the number of traffic enforcement units to investigate the illegal bus fares. Such illegal pickups bring large safety risks. The alert pickup locations and try to arrest bus drivers who are functions offered by the current vehicle tracking systems barely conducting illegal pickups on site. An effective site can catch this illegal act, and few studies of detecting driving investigation requires long-term experience from traffic police anomaly from GPS data focus on it either. This study hereby and takes large time and labor costs, which call for assistance presents an initial effort to fill the gap. We propose an approach from modern technology of intelligent transportation systems to automatically detecting suspicious pickup locations from (ITS). intercity bus GPS traces, and implement the approach in a geographical information system. A case study demonstrates the This study develops a geographical information system for effectiveness of the system with its high accuracy of detecting traffic police (GIS-TP) to automatically detect suspicious illegal pickup locations, and its functionality to help traffic pickup locations from intercity bus GPS traces. -

The Urban Rail Development Handbook
DEVELOPMENT THE “ The Urban Rail Development Handbook offers both planners and political decision makers a comprehensive view of one of the largest, if not the largest, investment a city can undertake: an urban rail system. The handbook properly recognizes that urban rail is only one part of a hierarchically integrated transport system, and it provides practical guidance on how urban rail projects can be implemented and operated RAIL URBAN THE URBAN RAIL in a multimodal way that maximizes benefits far beyond mobility. The handbook is a must-read for any person involved in the planning and decision making for an urban rail line.” —Arturo Ardila-Gómez, Global Lead, Urban Mobility and Lead Transport Economist, World Bank DEVELOPMENT “ The Urban Rail Development Handbook tackles the social and technical challenges of planning, designing, financing, procuring, constructing, and operating rail projects in urban areas. It is a great complement HANDBOOK to more technical publications on rail technology, infrastructure, and project delivery. This handbook provides practical advice for delivering urban megaprojects, taking account of their social, institutional, and economic context.” —Martha Lawrence, Lead, Railway Community of Practice and Senior Railway Specialist, World Bank HANDBOOK “ Among the many options a city can consider to improve access to opportunities and mobility, urban rail stands out by its potential impact, as well as its high cost. Getting it right is a complex and multifaceted challenge that this handbook addresses beautifully through an in-depth and practical sharing of hard lessons learned in planning, implementing, and operating such urban rail lines, while ensuring their transformational role for urban development.” —Gerald Ollivier, Lead, Transit-Oriented Development Community of Practice, World Bank “ Public transport, as the backbone of mobility in cities, supports more inclusive communities, economic development, higher standards of living and health, and active lifestyles of inhabitants, while improving air quality and liveability. -
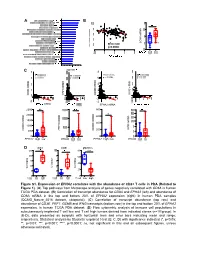
B and IFNG Transcripts (Bottom Row) in the Top and Bottom 20% of EPHA2 Expression, in Human TCGA PDA Dataset
A B mRNA CD8A C 8 R2=0.03705 6 p = 0.0098 4 2 mRNA IFNG -2 2468 -2 EPHA2 mRNA 2500 ** 800 2000 600 * 1500 400 mRNA 1000 200 IFNG 500 0 0 EPHA2 high low EPHA2 high low D gMDSCs 80 *** 60 40 % CD45+ 20 0 T cell low high Figure S1. Expression of EPHA2 correlates with the abundance of CD8+ T cells in PDA (Related to Figure 1). (A) Top pathways from Metascape analysis of genes negatively correlated with CD8A in human TCGA PDA dataset. (B) Correlation of transcript abundance for CD8A and EPHA2 (left) and abundance of CD8A mRNA in the top and bottom 20% of EPHA2 expression (right) in human PDA samples (QCMG_Nature_2016 dataset, cbioportal). (C) Correlation of transcript abundance (top row) and abundance of CD3E, PRF1, GZMB and IFNG transcripts (bottom row) in the top and bottom 20% of EPHA2 expression, in human TCGA PDA dataset. (D) Flow cytometric analysis of immune cell populations in subcutaneously implanted T cell low and T cell high tumors derived from indicated clones (n=10/group). In (B-D), data presented as boxplots with horizontal lines and error bars indicating mean and range, respectively. Statistical analysis by Students’ unpaired t-test (B, C, D) with significance indicated (*, p<0.05; **, p<0.01; ***, p<0.001; ****, p<0.0001; ns, not significant in this and all subsequent figures, unless otherwise indicated). A EPHA2 staining B 6419c5 6694c2 Ctrl WT % YFP+ Epha2-WT KO1 KO2 Epha2-KO C CD8+/myeloid cells CD8+/gMDSC D Macs cDC CD103+ cDC 40 30 20 10 CD103+ (% CD45+) CD8+/CD11b+MHCII- 0 6419c5 6694c2 E CD8+/myeloid cells CD8+/gMDSCF Macs cDC CD103+ 2.5 2.0 1.5 *** 1.0 0.5 CD103+ (% CD45+) CD103+ (% CD8+/CD11b+MHCII- 0.0 6419c5 6694c2 G Arginase 1+ IDO1+ iNOS+ H Arginase 1+ IDO1+ iNOS+ CD206+ 25 100 40 ** *** *** 20 80 30 15 60 20 10 40 10 5 % F480+ Macs Macs F480+ % 20 0 0 0 6419c5 6419c5 6419c5 6419c5 6419c5 6419c5 6419c5 IKJL 1000 *** 800 600 400 *** 200 0 6419c5 6694c2 Figure S2. -

The Mobility Opportunity Improving Public Transport to Drive Economic Growth
The Mobility Opportunity Improving public transport to drive economic growth. A research project commissioned by Siemens AG Contents 1. Executive summary 5 Why transport matters 5 A unique study 5 Key findings 6 Pointers for investment strategies 7 2. How the study was conducted 9 Scope of study 9 The true cost of transport 9 High-level approach 10 Economic audit 10 3. The economic opportunity 11 Cost and the size of the prize today 11 How cost and opportunity will change by 2030 13 4. How cities compare 17 Well-established cities 17 High density compact centres 17 Emerging cities 19 5. Pointers for investment strategies 21 The scale of the opportunity should dictate the level of investment 21 Using technology to improve quality may be the best route to economic uplift 24 Urban rail networks are a key way for larger cities to meet capacity demand 25 Integrated governance is crucial in planning and operating an efficient network 27 Appendix 1: Selected investment cases 29 Appendix 2: City profiles 35 Appendix 3: Methodology 71 Overview of approach 71 Key principles 72 Appendix 4: Technical audit 75 3 “Efficient transport can attract economic activity to cities, and boost productivity by improving connectivity and reducing time lost to travel” 4 1. Executive Summary Why transport matters cities face a need to upgrade and supplement existing infrastructure to meet modern requirements. Transport plays a key role in economic growth Cities account for around 80% of the world’s economic In other cities, such as Tokyo and Seoul, relatively recent output, and drive an even higher share of global growth. -

Issue #30, March 2021
High-Speed Intercity Passenger SPEEDLINESMarch 2021 ISSUE #30 Moynihan is a spectacular APTA’S CONFERENCE SCHEDULE » p. 8 train hall for Amtrak, providing additional access to Long Island Railroad platforms. Occupying the GLOBAL RAIL PROJECTS » p. 12 entirety of the superblock between Eighth and Ninth Avenues and 31st » p. 26 and 33rd Streets. FRICTIONLESS, HIGH-SPEED TRANSPORTATION » p. 5 APTA’S PHASE 2 ROI STUDY » p. 39 CONTENTS 2 SPEEDLINES MAGAZINE 3 CHAIRMAN’S LETTER On the front cover: Greetings from our Chair, Joe Giulietti INVESTING IN ENVIRONMENTALLY FRIENDLY AND ENERGY-EFFICIENT HIGH-SPEED RAIL PROJECTS WILL CREATE HIGHLY SKILLED JOBS IN THE TRANS- PORTATION INDUSTRY, REVITALIZE DOMESTIC 4 APTA’S CONFERENCE INDUSTRIES SUPPLYING TRANSPORTATION PROD- UCTS AND SERVICES, REDUCE THE NATION’S DEPEN- DENCY ON FOREIGN OIL, MITIGATE CONGESTION, FEATURE ARTICLE: AND PROVIDE TRAVEL CHOICES. 5 MOYNIHAN TRAIN HALL 8 2021 CONFERENCE SCHEDULE 9 SHARED USE - IS IT THE ANSWER? 12 GLOBAL RAIL PROJECTS 24 SNIPPETS - IN THE NEWS... ABOVE: For decades, Penn Station has been the visible symbol of official disdain for public transit and 26 FRICTIONLESS HIGH-SPEED TRANS intercity rail travel, and the people who depend on them. The blight that is Penn Station, the new Moynihan Train Hall helps knit together Midtown South with the 31 THAILAND’S FIRST PHASE OF HSR business district expanding out from Hudson Yards. 32 AMTRAK’S BIKE PROGRAM CHAIR: JOE GIULIETTI VICE CHAIR: CHRIS BRADY SECRETARY: MELANIE K. JOHNSON OFFICER AT LARGE: MICHAEL MCLAUGHLIN 33