1 CHAPTER 22 DIMENSIONS 22.1 Mass, Length and Time Any
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Metric System Units of Length
Math 0300 METRIC SYSTEM UNITS OF LENGTH Þ To convert units of length in the metric system of measurement The basic unit of length in the metric system is the meter. All units of length in the metric system are derived from the meter. The prefix “centi-“means one hundredth. 1 centimeter=1 one-hundredth of a meter kilo- = 1000 1 kilometer (km) = 1000 meters (m) hecto- = 100 1 hectometer (hm) = 100 m deca- = 10 1 decameter (dam) = 10 m 1 meter (m) = 1 m deci- = 0.1 1 decimeter (dm) = 0.1 m centi- = 0.01 1 centimeter (cm) = 0.01 m milli- = 0.001 1 millimeter (mm) = 0.001 m Conversion between units of length in the metric system involves moving the decimal point to the right or to the left. Listing the units in order from largest to smallest will indicate how many places to move the decimal point and in which direction. Example 1: To convert 4200 cm to meters, write the units in order from largest to smallest. km hm dam m dm cm mm Converting cm to m requires moving 4 2 . 0 0 2 positions to the left. Move the decimal point the same number of places and in the same direction (to the left). So 4200 cm = 42.00 m A metric measurement involving two units is customarily written in terms of one unit. Convert the smaller unit to the larger unit and then add. Example 2: To convert 8 km 32 m to kilometers First convert 32 m to kilometers. km hm dam m dm cm mm Converting m to km requires moving 0 . -

Lesson 1: Length English Vs
Lesson 1: Length English vs. Metric Units Which is longer? A. 1 mile or 1 kilometer B. 1 yard or 1 meter C. 1 inch or 1 centimeter English vs. Metric Units Which is longer? A. 1 mile or 1 kilometer 1 mile B. 1 yard or 1 meter C. 1 inch or 1 centimeter 1.6 kilometers English vs. Metric Units Which is longer? A. 1 mile or 1 kilometer 1 mile B. 1 yard or 1 meter C. 1 inch or 1 centimeter 1.6 kilometers 1 yard = 0.9444 meters English vs. Metric Units Which is longer? A. 1 mile or 1 kilometer 1 mile B. 1 yard or 1 meter C. 1 inch or 1 centimeter 1.6 kilometers 1 inch = 2.54 centimeters 1 yard = 0.9444 meters Metric Units The basic unit of length in the metric system in the meter and is represented by a lowercase m. Standard: The distance traveled by light in absolute vacuum in 1∕299,792,458 of a second. Metric Units 1 Kilometer (km) = 1000 meters 1 Meter = 100 Centimeters (cm) 1 Meter = 1000 Millimeters (mm) Which is larger? A. 1 meter or 105 centimeters C. 12 centimeters or 102 millimeters B. 4 kilometers or 4400 meters D. 1200 millimeters or 1 meter Measuring Length How many millimeters are in 1 centimeter? 1 centimeter = 10 millimeters What is the length of the line in centimeters? _______cm What is the length of the line in millimeters? _______mm What is the length of the line to the nearest centimeter? ________cm HINT: Round to the nearest centimeter – no decimals. -

Distances in the Solar System Are Often Measured in Astronomical Units (AU). One Astronomical Unit Is Defined As the Distance from Earth to the Sun
Distances in the solar system are often measured in astronomical units (AU). One astronomical unit is defined as the distance from Earth to the Sun. 1 AU equals about 150 million km (93 million miles). Table below shows the distance from the Sun to each planet in AU. The table shows how long it takes each planet to spin on its axis. It also shows how long it takes each planet to complete an orbit. Notice how slowly Venus rotates! A day on Venus is actually longer than a year on Venus! Distances to the Planets and Properties of Orbits Relative to Earth's Orbit Average Distance Length of Day (In Earth Length of Year (In Earth Planet from Sun (AU) Days) Years) Mercury 0.39 AU 56.84 days 0.24 years Venus 0.72 243.02 0.62 Earth 1.00 1.00 1.00 Mars 1.52 1.03 1.88 Jupiter 5.20 0.41 11.86 Saturn 9.54 0.43 29.46 Uranus 19.22 0.72 84.01 Neptune 30.06 0.67 164.8 The Role of Gravity Planets are held in their orbits by the force of gravity. What would happen without gravity? Imagine that you are swinging a ball on a string in a circular motion. Now let go of the string. The ball will fly away from you in a straight line. It was the string pulling on the ball that kept the ball moving in a circle. The motion of a planet is very similar to the ball on a strong. -

Measuring the Astronomical Unit from Your Backyard Two Astronomers, Using Amateur Equipment, Determined the Scale of the Solar System to Better Than 1%
Measuring the Astronomical Unit from Your Backyard Two astronomers, using amateur equipment, determined the scale of the solar system to better than 1%. So can you. By Robert J. Vanderbei and Ruslan Belikov HERE ON EARTH we measure distances in millimeters and throughout the cosmos are based in some way on distances inches, kilometers and miles. In the wider solar system, to nearby stars. Determining the astronomical unit was as a more natural standard unit is the tUlronomical unit: the central an issue for astronomy in the 18th and 19th centu· mean distance from Earth to the Sun. The astronomical ries as determining the Hubble constant - a measure of unit (a.u.) equals 149,597,870.691 kilometers plus or minus the universe's expansion rate - was in the 20th. just 30 meters, or 92,955.807.267 international miles plus or Astronomers of a century and more ago devised various minus 100 feet, measuring from the Sun's center to Earth's ingenious methods for determining the a. u. In this article center. We have learned the a. u. so extraordinarily well by we'll describe a way to do it from your backyard - or more tracking spacecraft via radio as they traverse the solar sys precisely, from any place with a fairly unobstructed view tem, and by bouncing radar Signals off solar.system bodies toward the east and west horizons - using only amateur from Earth. But we used to know it much more poorly. equipment. The method repeats a historic experiment per This was a serious problem for many brancht:s of as formed by Scottish astronomer David Gill in the late 19th tronomy; the uncertain length of the astronomical unit led century. -

Multidisciplinary Design Project Engineering Dictionary Version 0.0.2
Multidisciplinary Design Project Engineering Dictionary Version 0.0.2 February 15, 2006 . DRAFT Cambridge-MIT Institute Multidisciplinary Design Project This Dictionary/Glossary of Engineering terms has been compiled to compliment the work developed as part of the Multi-disciplinary Design Project (MDP), which is a programme to develop teaching material and kits to aid the running of mechtronics projects in Universities and Schools. The project is being carried out with support from the Cambridge-MIT Institute undergraduate teaching programe. For more information about the project please visit the MDP website at http://www-mdp.eng.cam.ac.uk or contact Dr. Peter Long Prof. Alex Slocum Cambridge University Engineering Department Massachusetts Institute of Technology Trumpington Street, 77 Massachusetts Ave. Cambridge. Cambridge MA 02139-4307 CB2 1PZ. USA e-mail: [email protected] e-mail: [email protected] tel: +44 (0) 1223 332779 tel: +1 617 253 0012 For information about the CMI initiative please see Cambridge-MIT Institute website :- http://www.cambridge-mit.org CMI CMI, University of Cambridge Massachusetts Institute of Technology 10 Miller’s Yard, 77 Massachusetts Ave. Mill Lane, Cambridge MA 02139-4307 Cambridge. CB2 1RQ. USA tel: +44 (0) 1223 327207 tel. +1 617 253 7732 fax: +44 (0) 1223 765891 fax. +1 617 258 8539 . DRAFT 2 CMI-MDP Programme 1 Introduction This dictionary/glossary has not been developed as a definative work but as a useful reference book for engi- neering students to search when looking for the meaning of a word/phrase. It has been compiled from a number of existing glossaries together with a number of local additions. -

Measuring in Metric Units BEFORE Now WHY? You Used Metric Units
Measuring in Metric Units BEFORE Now WHY? You used metric units. You’ll measure and estimate So you can estimate the mass using metric units. of a bike, as in Ex. 20. Themetric system is a decimal system of measurement. The metric Word Watch system has units for length, mass, and capacity. metric system, p. 80 Length Themeter (m) is the basic unit of length in the metric system. length: meter, millimeter, centimeter, kilometer, Three other metric units of length are themillimeter (mm) , p. 80 centimeter (cm) , andkilometer (km) . mass: gram, milligram, kilogram, p. 81 You can use the following benchmarks to estimate length. capacity: liter, milliliter, kiloliter, p. 82 1 millimeter 1 centimeter 1 meter thickness of width of a large height of the a dime paper clip back of a chair 1 kilometer combined length of 9 football fields EXAMPLE 1 Using Metric Units of Length Estimate the length of the bandage by imagining paper clips laid next to it. Then measure the bandage with a metric ruler to check your estimate. 1 Estimate using paper clips. About 5 large paper clips fit next to the bandage, so it is about 5 centimeters long. ch O at ut! W 2 Measure using a ruler. A typical metric ruler allows you to measure Each centimeter is divided only to the nearest tenth of into tenths, so the bandage cm 12345 a centimeter. is 4.8 centimeters long. 80 Chapter 2 Decimal Operations Mass Mass is the amount of matter that an object has. The gram (g) is the basic metric unit of mass. -

Hydraulics Manual Glossary G - 3
Glossary G - 1 GLOSSARY OF HIGHWAY-RELATED DRAINAGE TERMS (Reprinted from the 1999 edition of the American Association of State Highway and Transportation Officials Model Drainage Manual) G.1 Introduction This Glossary is divided into three parts: · Introduction, · Glossary, and · References. It is not intended that all the terms in this Glossary be rigorously accurate or complete. Realistically, this is impossible. Depending on the circumstance, a particular term may have several meanings; this can never change. The primary purpose of this Glossary is to define the terms found in the Highway Drainage Guidelines and Model Drainage Manual in a manner that makes them easier to interpret and understand. A lesser purpose is to provide a compendium of terms that will be useful for both the novice as well as the more experienced hydraulics engineer. This Glossary may also help those who are unfamiliar with highway drainage design to become more understanding and appreciative of this complex science as well as facilitate communication between the highway hydraulics engineer and others. Where readily available, the source of a definition has been referenced. For clarity or format purposes, cited definitions may have some additional verbiage contained in double brackets [ ]. Conversely, three “dots” (...) are used to indicate where some parts of a cited definition were eliminated. Also, as might be expected, different sources were found to use different hyphenation and terminology practices for the same words. Insignificant changes in this regard were made to some cited references and elsewhere to gain uniformity for the terms contained in this Glossary: as an example, “groundwater” vice “ground-water” or “ground water,” and “cross section area” vice “cross-sectional area.” Cited definitions were taken primarily from two sources: W.B. -

International System of Units (SI)
International System of Units (SI) National Institute of Standards and Technology (www.nist.gov) Multiplication Prefix Symbol factor 1018 exa E 1015 peta P 1012 tera T 109 giga G 106 mega M 103 kilo k 102 * hecto h 101 * deka da 10-1 * deci d 10-2 * centi c 10-3 milli m 10-6 micro µ 10-9 nano n 10-12 pico p 10-15 femto f 10-18 atto a * Prefixes of 100, 10, 0.1, and 0.01 are not formal SI units From: Downs, R.J. 1988. HortScience 23:881-812. International System of Units (SI) Seven basic SI units Physical quantity Unit Symbol Length meter m Mass kilogram kg Time second s Electrical current ampere A Thermodynamic temperature kelvin K Amount of substance mole mol Luminous intensity candela cd Supplementary SI units Physical quantity Unit Symbol Plane angle radian rad Solid angle steradian sr From: Downs, R.J. 1988. HortScience 23:881-812. International System of Units (SI) Derived SI units with special names Physical quantity Unit Symbol Derivation Absorbed dose gray Gy J kg-1 Capacitance farad F A s V-1 Conductance siemens S A V-1 Disintegration rate becquerel Bq l s-1 Electrical charge coulomb C A s Electrical potential volt V W A-1 Energy joule J N m Force newton N kg m s-2 Illumination lux lx lm m-2 Inductance henry H V s A-1 Luminous flux lumen lm cd sr Magnetic flux weber Wb V s Magnetic flux density tesla T Wb m-2 Pressure pascal Pa N m-2 Power watt W J s-1 Resistance ohm Ω V A-1 Volume liter L dm3 From: Downs, R.J. -

Measuring Length, Mass, Volume, and Temperature Label Your (Adapted from Prentice-Hall, Inc
Name______________________________ Class __________________ Date ______________ Don’t forget to Measuring Length, Mass, Volume, and Temperature label your (Adapted from Prentice-Hall, Inc. Biology Lab Manual B) answers with the correct units! Introduction : Doing experiments is an important part of science. Most experiments include making measurements. Many different quantities can be measured. Some examples are length, mass, volume, temperature, and time. Some quantities, such as length, can be measured directly. Others, such as speed, are calculated from other measurements. In science you will probably use metric units to estimate, measure, and record data. The three fundamental metric units are the meter for length, the gram for mass, and the liter for capacity. In this investigation you will carry out different types of measurements. Problem : What types of measurements are used to describe quantities? Pre-Lab Discussion: Read the entire investigation. Then, work with a partner to answer the following questions. 1. How will you record a distance that is 2 centimeters longer than 5 meters? ________ 2 centimeters shorter? _______ 2. Why would you measure the contents of a paper cup in milliliters (mL) rather than in liters? 3. Explain why don’t measurements start at the beginning of a ruler, yard stick, meter stick, etc? (the zero point is always a little bit offset from the end) Materials (per group): meter stick 2 paper cups millimeter ruler 30 cm of string 250-mL graduated cylinder golf ball tripple beam balance 1 sheet college-ruled notebook paper thermometer Toy car (like a hotwheels car) Safety : Wear your lab apron and safety goggles while dealing with glassware. -

Glossary of Materials Engineering Terminology
Glossary of Materials Engineering Terminology Adapted from: Callister, W. D.; Rethwisch, D. G. Materials Science and Engineering: An Introduction, 8th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, 2010. McCrum, N. G.; Buckley, C. P.; Bucknall, C. B. Principles of Polymer Engineering, 2nd ed.; Oxford University Press: New York, NY, 1997. Brittle fracture: fracture that occurs by rapid crack formation and propagation through the material, without any appreciable deformation prior to failure. Crazing: a common response of plastics to an applied load, typically involving the formation of an opaque banded region within transparent plastic; at the microscale, the craze region is a collection of nanoscale, stress-induced voids and load-bearing fibrils within the material’s structure; craze regions commonly occur at or near a propagating crack in the material. Ductile fracture: a mode of material failure that is accompanied by extensive permanent deformation of the material. Ductility: a measure of a material’s ability to undergo appreciable permanent deformation before fracture; ductile materials (including many metals and plastics) typically display a greater amount of strain or total elongation before fracture compared to non-ductile materials (such as most ceramics). Elastic modulus: a measure of a material’s stiffness; quantified as a ratio of stress to strain prior to the yield point and reported in units of Pascals (Pa); for a material deformed in tension, this is referred to as a Young’s modulus. Engineering strain: the change in gauge length of a specimen in the direction of the applied load divided by its original gauge length; strain is typically unit-less and frequently reported as a percentage. -

Measuring Length, Mass, Volume, and Temperature
Name______________________________ Class __________________ Date ______________ Chapter 1 The Science of Biology You may want to refer students to Measuring Length, Mass, Volume, Section 1–4 and Appendix C in the textbook for a discussion of and Temperature measurement. Time required: 40 minutes Introduction Doing experiments is an important part of science. Most experiments include making measurements. Many different quantities can be measured. Some examples are length, mass, volume, temperature, and time. Some quantities, such as length, can be measured directly. Others, such as speed, are calculated from other measurements. In science you will probably use metric units to estimate, measure, and record data. The three fundamental metric units are the meter for length, the gram for mass, and the liter for capacity. In this investigation you will carry out different types of measurements. Problem What types of measurements are used to describe quantities? Pre-Lab Discussion Read the entire investigation. Then, work with a partner to answer the following questions. 1. Which of the measurements in the investigation are familiar to you? Which will be new to you? Measuring mass and liquid volume may be less familiar to students than measuring length and temperature. 2. How will you record a distance that is 2 centimeters longer than 5 meters? 2 centimeters shorter? 5.02 m (or 5 m 2 cm); 4.98 m (or 4 m 98 cm). Remind students that 1 cm equals 0.01 m. If necessary, review converting between centimeters and meters. 3. How will you choose an object to measure in millimeters? Millimeters are very small, so the length to be measured should not be too large. -
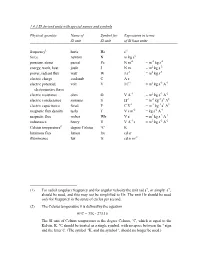
1.4.3 SI Derived Units with Special Names and Symbols
1.4.3 SI derived units with special names and symbols Physical quantity Name of Symbol for Expression in terms SI unit SI unit of SI base units frequency1 hertz Hz s-1 force newton N m kg s-2 pressure, stress pascal Pa N m-2 = m-1 kg s-2 energy, work, heat joule J N m = m2 kg s-2 power, radiant flux watt W J s-1 = m2 kg s-3 electric charge coulomb C A s electric potential, volt V J C-1 = m2 kg s-3 A-1 electromotive force electric resistance ohm Ω V A-1 = m2 kg s-3 A-2 electric conductance siemens S Ω-1 = m-2 kg-1 s3 A2 electric capacitance farad F C V-1 = m-2 kg-1 s4 A2 magnetic flux density tesla T V s m-2 = kg s-2 A-1 magnetic flux weber Wb V s = m2 kg s-2 A-1 inductance henry H V A-1 s = m2 kg s-2 A-2 Celsius temperature2 degree Celsius °C K luminous flux lumen lm cd sr illuminance lux lx cd sr m-2 (1) For radial (angular) frequency and for angular velocity the unit rad s-1, or simply s-1, should be used, and this may not be simplified to Hz. The unit Hz should be used only for frequency in the sense of cycles per second. (2) The Celsius temperature θ is defined by the equation θ/°C = T/K - 273.15 The SI unit of Celsius temperature is the degree Celsius, °C, which is equal to the Kelvin, K.