DOCSLIB.ORG

Relativistic Quantum Chemistry

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text

Load more

Relativistic Quantum Chemistry Valérie Vallet ([email protected]) CNRS, Lille University, France Outline ▸ Why do relativistic effects become significant when the atomic number Z increases? ▸ How to account for relativistic effects in quantum chemistry? ▸ Which role do relativistic effects play in the chemistry across the periodic table ? ✴ Bond lengths, frequencies ✴ Binding energies, reaction barriers ✴ Spectroscopy ✴ Ionization potentials, electron affinities ✴ NMR properties Relativistic Quantum Chemistry | Valérie Vallet @ CNRS Uni. Lille 2 Relevance and nature of relativistic effects Can you spot the difference? Property Ag Au Electronic configuration [Kr] 4d105s1 [Xe] 4f14 5d10 6s1 Crystal structure FCC FCC Color silver golden Why does gold look so… golden? Relativistic Quantum Chemistry | Valérie Vallet @ CNRS Uni. Lille 4 Have a look at relativistic effects in chemistry Chem. Rev. 1988. 88. 563-594 583 Relativistic Effects in Structural Chemistry EKKA PYYKKO Department of chemistry. Uinh'ersity of Helsinki, Et. Hesperiankatu 4, 00100 Helsinki, FWand' Received March 17, 1987 (Revised Manuscript Received July 7, 1987) Contents I. Introduction 563 11. Theory and Methods 565 A. Fundamental Questions 565 B. Properties of Individual Atoms 565 C. Available Quantum Chemical Methods for 567 Molecules 0. Effectson Bond Lengths 571 111. Molecular Geometries 573 A. Bond Lengths 573 B. Bond Angles 577 C. Catalysis and Reaction Pathways 577 D. Solids 578 pekka pwkko was bom in 1941 in Hinnerjoki. Finland. and recehed E. The Inert-Pair Effect 578 his FiLKand.. FiLLic.. and FIl.dr from the Unhrersity of Turku. After IV. Other Properties 580 working at We UnWisof Aafhus, Gatebwg. Helsinki. Jyviisky!A, A. Force Constants 580 Paris XI, and Oulu (1968-1974). he became Associate Professor B. Dlssoclatlon Energies 580 of Quantum Chemistry at Abo Akademi in Turku in 1974. Since C. Splittings 582 1984 he has been Professor of Chemistry at the University of Finestructure Hekinki. Finland. where he holds We "Swedish Chair of Chemistry". D. Ionization Potentials, Electron Affinities, 582 founded in 1908 as a parallel one to Johan Gadolin's former chair, and Photoelectron Spectra established in 1761. His main interests have been NMR meorY and E. Colors 583 relativistic quantum chemistry F. Charge Distributions and Molecular 563 Relativistic Quantum Chemistry | Valérie Vallet @ CNRS Uni. Lille 5 Moments the relativistic mass increase G. Magnetic Resonance Parameters 583 V. Further Possible Examples and Open Problems 585 m = mo/(l - (U/C))1'* (la) VI. Summary: Relativistic Effects in the Periodic 587 Table mo being the rest mass and u the speed of the electron, VII. References 587 the effective Bohr radius, a. = (4rc0)(h2/me2) (W I. Introducflon will decrease for inner electrons with large average The two basic theories of modem physics are the speeds. For a 1s shell at the nonrelativistic limit, this theory of relativity and quantum mechanics. While the average speed is 2 au. Thus the 1s electron of Hg has importance of the latter in chemistry was instantly a u/c of 80/137 = 0.58, implying a radial shrinkage by recognized, it was not until the 19708 that the full 23%. Because the higher s shells have to be orthogonal relevance of relativistic effects in heavy-element chem- against the lower ones, they will suffer a similar con- istry was discovered. traction. Due to interacting relativistic and shell- For very precise calculations, relativistic energy con- structure effects, their contraction can in fact he even tributions are already needed for H2+or H,. They in- larger; for gold, the 6s shell has larger (percental) re- crease, for valence shells, roughly like .??. Depending lativistic effects than the Is shell. on the accuracy achieved in the calculation, they be- For readers not convinced by a qualitative argument, come relevant again around Cu, or perhaps Ag. For the we can consider an exactly solvable problem: the hy- sixth row (around W to Bi), relativistic effects are drogen-like atom with 2 = 80 in Figure 1. As seen, the comparable to the usual shell-structure effects and contractions are comparable for the three firsts shells. provide an explanation for much of the basic freshman Alternatively, to understand the valence electron chemistry of these elements. For the existing actinoids effects in a many-electron atom, one can compare (see relativistic effects are essential. ref 35) the relativistic (Dirac) and nonrelativistic The relativistic effects can be defined as anything (Schrodinger) dynamics for the valence electron in a arising from the finite speed of light, c = 137.035 989 5 given atomic potential, to study the importance of the (61)au4I5, as compared to c = m. The basic theory is direct relativistic effect. The (originally surprising) discussed in section 11. result" was that this is the main effect for the 6s of Au It has become a tradition to introduce the reader to or the 6p* (=6p,/,) of TI. The relativistic change of the qualitative effects of relativity as follows: Due to the atomic potential mattered less than the direct, dy- 0009-2665/88/078&0563$06.50/0 0 1988 American Chemical Society Chem. Rev. 1988. 88. 563-594 583 Relativistic Effects in Structural Chemistry EKKA PYYKKO Department of chemistry. Uinh'ersity of Helsinki, Et. Hesperiankatu 4, 00100 Helsinki, FWand' Received March 17, 1987 (Revised Manuscript Received July 7, 1987) Contents I. Introduction 563 11. Theory and Methods 565 A. Fundamental Questions 565 B. Properties of Individual Atoms 565 C. Available Quantum Chemical Methods for 567 Molecules 0. Effectson Bond Lengths 571 111. Molecular Geometries 573 A. Bond Lengths 573 B. Bond Angles 577 C. Catalysis and Reaction Pathways 577 D. Solids 578 pekka pwkko was bom in 1941 in Hinnerjoki. Finland. and recehed E. The Inert-Pair Effect 578 his FiLKand.. FiLLic.. and FIl.dr from the Unhrersity of Turku. After IV. Other Properties 580 working at We UnWisof Aafhus, Gatebwg. Helsinki. Jyviisky!A, A. Force Constants 580 Paris XI, and Oulu (1968-1974). he became Associate Professor B. Dlssoclatlon Energies 580 of Quantum Chemistry at Abo Akademi in Turku in 1974. Since C. Splittings 582 1984 he has been Professor of Chemistry at the University of Finestructure Hekinki. Finland. where he holds We "Swedish Chair of Chemistry". D. Ionization Potentials, Electron Affinities, 582 founded in 1908 as a parallel one to Johan Gadolin's former chair, and Photoelectron Spectra established in 1761. His main interests have been NMR meorY and E. Colors 583 relativistic quantum chemistry F. Charge Distributions and Molecular 563 Moments the relativistic mass increase G. Magnetic Resonance Parameters 583 V. Further Possible Examples and Open Problems 585 m = mo/(l - (U/C))1'* (la) VI. Summary: Relativistic Effects in the Periodic 587 Table mo being the rest mass and u the speed of the electron, VII. References 587 the effective Bohr radius, a. = (4rc0)(h2/me2) (W RelativisticI. Introducflon effects in chemistry will decrease for inner electrons with large average The two basic theories of modem physics are the speeds. For a 1s shell at the nonrelativistic limit, this theory of relativity and quantum mechanics. While the average speed is 2 au. Thus the 1s electron of Hg has importance of the latter in chemistry was instantly a u/c of 80/137 = 0.58, implying a radial shrinkage by recognized, it was not until the 19708 that the full P. 23%.Pyykkö, Because Chem. Rev. the 1988,higher 88, s shells563 have to be orthogonal relevance of relativistic effects in heavy-element chem- against the lower ones, they will suffer a similar con- istry was discovered. traction. Due to interacting relativistic and shell- For very precise calculations, relativistic energy con- structure effects, their contraction can in fact he even tributions are already needed for H2+or H,. They in- larger; for gold, the 6s shell has larger (percental) re- crease, for valence shells, roughly like .??. Depending lativistic effects than the Is shell. ▸ Relativistic effects ariseon fromthe accuracy the finite achieved speed in the calculation, of light (cthey ≈ be- 137 a.u.)For readers not convinced by a qualitative argument, come relevant again around Cu, or perhaps Ag. For the we can consider an exactly solvable problem: the hy- sixth row (around W to Bi), relativistic effects are drogen-like atom with 2 = 80 in Figure 1. As seen, the ▸ v(1s) ∼ Z a.u. comparable to the usual shell-structure effects and contractions are comparable for the three firsts shells. provide an explanation for much of the basic freshman Alternatively, to understand the valence electron chemistry of these elements. For the existing actinoids effects in a many-electron atom, one can compare (see ▸ The relativistic mass increaserelativistic foreffects electrons are essential. with rest mass m0 andref 35) speed the relativistic v is (Dirac) and nonrelativistic The relativistic effects can be defined as anything (Schrodinger) dynamics for the valence electron in a arising from the finite speed of light, c = 137.035 989 5 given atomic potential, to study the importance of the m0 au4I5,as compared to c = m. The basic theory is direct relativistic effect. The (originally surprising) (61) m = γm0 = discussed in section 11. 2 result" was that this is the main effect for the 6s of Au It has become a tradition to introduceZ the reader to or the 6p* (=6p,/,) of TI. The relativistic change of the qualitative effects of relativity1 as follows:2 Due to the atomic potential mattered less than the direct, dy- r − c 0009-2665/88/078&0563$06.50/0 0 1988 American Chemical Society ▸ The Bohr radius is inversely proportional to electron mass: 2 4⇡"0~ a = 0 m ▸ Relativity will contract orbitals of one-electron atoms, e.g., Au78+ (Z/c = 57%), 18% relativistic contraction of the 1s orbital.
Recommended publications
  • Chem Compute Quickstart

    Chem Compute Quickstart

    Chem Compute Quickstart Chem Compute is maintained by Mark Perri at Sonoma State University and hosted on Jetstream at Indiana University. The Chem Compute URL is https://chemcompute.org/. We will use Chem Compute as the frontend for running electronic structure calculations with The General Atomic and Molecular Electronic Structure System, GAMESS (http://www.msg.ameslab.gov/gamess/). Chem Compute also provides access to other computational chemistry resources including PSI4 and the molecular dynamics packages TINKER and NAMD, though we will not be using those resource at this time. Follow this link, https://chemcompute.org/gamess/submit, to directly access the Chem Compute GAMESS guided submission interface. If you are a returning Chem Computer user, please log in now. If your University is part of the InCommon Federation you can log in without registering by clicking Login then "Log In with Google or your University" – select your University from the dropdown list. Otherwise if this is your first time working with Chem Compute, please register as a Chem Compute user by clicking the “Register” link in the top-right corner of the page. This gives you access to all of the computational resources available at ChemCompute.org and will allow you to maintain copies of your calculations in your user “Dashboard” that you can refer to later. Registering also helps track usage and obtain the resources needed to continue providing its service. When logged in with the GAMESS-Submit tabs selected, an instruction section appears on the left side of the page with instructions for several different kinds of calculations.
  • Dirac Equation - Wikipedia

    Dirac Equation - Wikipedia

    Dirac equation - Wikipedia https://en.wikipedia.org/wiki/Dirac_equation Dirac equation From Wikipedia, the free encyclopedia In particle physics, the Dirac equation is a relativistic wave equation derived by British physicist Paul Dirac in 1928. In its free form, or including electromagnetic interactions, it 1 describes all spin-2 massive particles such as electrons and quarks for which parity is a symmetry. It is consistent with both the principles of quantum mechanics and the theory of special relativity,[1] and was the first theory to account fully for special relativity in the context of quantum mechanics. It was validated by accounting for the fine details of the hydrogen spectrum in a completely rigorous way. The equation also implied the existence of a new form of matter, antimatter, previously unsuspected and unobserved and which was experimentally confirmed several years later. It also provided a theoretical justification for the introduction of several component wave functions in Pauli's phenomenological theory of spin; the wave functions in the Dirac theory are vectors of four complex numbers (known as bispinors), two of which resemble the Pauli wavefunction in the non-relativistic limit, in contrast to the Schrödinger equation which described wave functions of only one complex value. Moreover, in the limit of zero mass, the Dirac equation reduces to the Weyl equation. Although Dirac did not at first fully appreciate the importance of his results, the entailed explanation of spin as a consequence of the union of quantum mechanics and relativity—and the eventual discovery of the positron—represents one of the great triumphs of theoretical physics.
  • A Tale of Three Equations: Breit, Eddington-Gaunt, and Two-Body

    A Tale of Three Equations: Breit, Eddington-Gaunt, and Two-Body

    View metadata, citation and similarA Tale papers of at Three core.ac.uk Equations: Breit, Eddington-Gaunt, and Two-Body Dirac brought to you by CORE Peter Van Alstine provided by CERN Document Server 12474 Sunny Glenn Drive, Moorpark, Ca. 90125 Horace W. Crater The University of Tennessee Space Institute Tullahoma,Tennessee 37388 G.Breit’s original paper of 1929 postulates the Breit equation as a correction to an earlier defective equation due to Eddington and Gaunt, containing a form of interaction suggested by Heisenberg and Pauli. We observe that manifestly covariant electromagnetic Two-Body Dirac equations previously obtained by us in the framework of Relativistic Constraint Mechanics reproduce the spectral results of the Breit equation but through an interaction structure that contains that of Eddington and Gaunt. By repeating for our equation the analysis that Breit used to demonstrate the superiority of his equation to that of Eddington and Gaunt, we show that the historically unfamiliar interaction structures of Two-Body Dirac equations (in Breit-like form) are just what is needed to correct the covariant Eddington Gaunt equation without resorting to Breit’s version of retardation. 1 I. INTRODUCTION Three score and seven years ago, Gregory Breit extended Dirac’s spin-1/2 wave equation to a system of two charged particles [1]. He formed his equation by summing two free-particle Dirac Hamiltonians with an interaction obtained by substituting Dirac α~’s for velocities in the semi-relativistic electrodynamic interaction of Darwin:. α 1 EΨ= α~ ·p~ +β m +α~ ·p~ +β m − [1 − (α~ · α~ + α~ · r~ˆ α ·rˆ)] Ψ.
  • Parameterizing a Novel Residue

    Parameterizing a Novel Residue

    University of Illinois at Urbana-Champaign Luthey-Schulten Group, Department of Chemistry Theoretical and Computational Biophysics Group Computational Biophysics Workshop Parameterizing a Novel Residue Rommie Amaro Brijeet Dhaliwal Zaida Luthey-Schulten Current Editors: Christopher Mayne Po-Chao Wen February 2012 CONTENTS 2 Contents 1 Biological Background and Chemical Mechanism 4 2 HisH System Setup 7 3 Testing out your new residue 9 4 The CHARMM Force Field 12 5 Developing Topology and Parameter Files 13 5.1 An Introduction to a CHARMM Topology File . 13 5.2 An Introduction to a CHARMM Parameter File . 16 5.3 Assigning Initial Values for Unknown Parameters . 18 5.4 A Closer Look at Dihedral Parameters . 18 6 Parameter generation using SPARTAN (Optional) 20 7 Minimization with new parameters 32 CONTENTS 3 Introduction Molecular dynamics (MD) simulations are a powerful scientific tool used to study a wide variety of systems in atomic detail. From a standard protein simulation, to the use of steered molecular dynamics (SMD), to modelling DNA-protein interactions, there are many useful applications. With the advent of massively parallel simulation programs such as NAMD2, the limits of computational anal- ysis are being pushed even further. Inevitably there comes a time in any molecular modelling scientist’s career when the need to simulate an entirely new molecule or ligand arises. The tech- nique of determining new force field parameters to describe these novel system components therefore becomes an invaluable skill. Determining the correct sys- tem parameters to use in conjunction with the chosen force field is only one important aspect of the process.
  • Arxiv:Hep-Ph/9412261V1 8 Dec 1994

    Arxiv:Hep-Ph/9412261V1 8 Dec 1994

    IPNO/TH 94-85 How to obtain a covariant Breit type equation from relativistic Constraint Theory J. Mourad Laboratoire de Mod`eles de Physique Math´ematique, Universit´ede Tours, Parc de Grandmont, F-37200 Tours, France H. Sazdjian Division de Physique Th´eorique∗, Institut de Physique Nucl´eaire, Universit´eParis XI, F-91406 Orsay Cedex, France arXiv:hep-ph/9412261v1 8 Dec 1994 October 1994 ∗Unit´ede Recherche des Universit´es Paris 11 et Paris 6 associ´ee au CNRS. 1 Abstract It is shown that, by an appropriate modification of the structure of the interaction po- tential, the Breit equation can be incorporated into a set of two compatible manifestly covariant wave equations, derived from the general rules of Constraint Theory. The com- plementary equation to the covariant Breit type equation determines the evolution law in the relative time variable. The interaction potential can be systematically calculated in perturbation theory from Feynman diagrams. The normalization condition of the Breit wave function is determined. The wave equation is reduced, for general classes of poten- tial, to a single Pauli-Schr¨odinger type equation. As an application of the covariant Breit type equation, we exhibit massless pseudoscalar bound state solutions, corresponding to a particular class of confining potentials. PACS numbers : 03.65.Pm, 11.10.St, 12.39.Ki. 2 1 Introduction Historically, The Breit equation [1] represents the first attempt to describe the relativistic dynamics of two interacting fermion systems. It consists in summing the free Dirac hamiltonians of the two fermions and adding mutual and, eventually, external potentials. This equation, when applied to QED, with one-photon exchange diagram considered in the Coulomb gauge, and solved in the linearized approximation, provides the correct spectra to order α4 [1, 2] for various bound state problems.
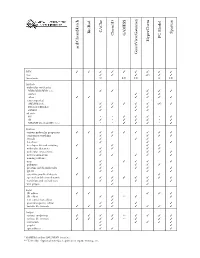
  • D:\Doc\Workshops\2005 Molecular Modeling\Notebook Pages\Software Comparison\Summary.Wpd

    D:\Doc\Workshops\2005 Molecular Modeling\Notebook Pages\Software Comparison\Summary.Wpd

    CAChe BioRad Spartan GAMESS Chem3D PC Model HyperChem acd/ChemSketch GaussView/Gaussian WIN TTTT T T T T T mac T T T (T) T T linux/unix U LU LU L LU Methods molecular mechanics MM2/MM3/MM+/etc. T T T T T Amber T T T other TT T T T T semi-empirical AM1/PM3/etc. T T T T T (T) T Extended Hückel T T T T ZINDO T T T ab initio HF * * T T T * T dft T * T T T * T MP2/MP4/G1/G2/CBS-?/etc. * * T T T * T Features various molecular properties T T T T T T T T T conformer searching T T T T T crystals T T T data base T T T developer kit and scripting T T T T molecular dynamics T T T T molecular interactions T T T T movies/animations T T T T T naming software T nmr T T T T T polymers T T T T proteins and biomolecules T T T T T QSAR T T T T scientific graphical objects T T spectral and thermodynamic T T T T T T T T transition and excited state T T T T T web plugin T T Input 2D editor T T T T T 3D editor T T ** T T text conversion editor T protein/sequence editor T T T T various file formats T T T T T T T T Output various renderings T T T T ** T T T T various file formats T T T T ** T T T animation T T T T T graphs T T spreadsheet T T T * GAMESS and/or GAUSSIAN interface ** Text only.
  • Solvable Two-Body Dirac Equation As a Potential Model of Light Mesons?

    Solvable Two-Body Dirac Equation As a Potential Model of Light Mesons?

    Symmetry, Integrability and Geometry: Methods and Applications SIGMA 4 (2008), 048, 19 pages Solvable Two-Body Dirac Equation as a Potential Model of Light Mesons? Askold DUVIRYAK Institute for Condensed Matter Physics of National Academy of Sciences of Ukraine, 1 Svientsitskii Str., UA–79011 Lviv, Ukraine E-mail: [email protected] Received October 29, 2007, in final form May 07, 2008; Published online May 30, 2008 Original article is available at http://www.emis.de/journals/SIGMA/2008/048/ Abstract. The two-body Dirac equation with general local potential is reduced to the pair of ordinary second-order differential equations for radial components of a wave function. The class of linear + Coulomb potentials with complicated spin-angular structure is found, for which the equation is exactly solvable. On this ground a relativistic potential model of light mesons is constructed and the mass spectrum is calculated. It is compared with experimental data. Key words: two body Dirac equation; Dirac oscillator; solvable model; Regge trajectories 2000 Mathematics Subject Classification: 81Q05; 34A05 1 Introduction It is well known that light meson spectra are structured into Regge trajectories which are approximately linear and degenerated due to a weak dependence of masses of resonances on their spin state. These features are reproduced well within the exactly solvable simple relativistic oscillator model (SROM) [1, 2, 3] describing two Klein–Gordon particles harmonically bound. Actually, mesons consist of quarks, i.e., spin-1/2 constituents. Thus potential models based on the Dirac equation are expected to be more appropriate for mesons spectroscopy. In recent years the two body Dirac equations (2BDE) in different formulations1 with various confining potentials are used as a relativistic constituent quark models [16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26].
  • Kepler Gpus and NVIDIA's Life and Material Science

    Kepler Gpus and NVIDIA's Life and Material Science

    LIFE AND MATERIAL SCIENCES Mark Berger; [email protected] Founded 1993 Invented GPU 1999 – Computer Graphics Visual Computing, Supercomputing, Cloud & Mobile Computing NVIDIA - Core Technologies and Brands GPU Mobile Cloud ® ® GeForce Tegra GRID Quadro® , Tesla® Accelerated Computing Multi-core plus Many-cores GPU Accelerator CPU Optimized for Many Optimized for Parallel Tasks Serial Tasks 3-10X+ Comp Thruput 7X Memory Bandwidth 5x Energy Efficiency How GPU Acceleration Works Application Code Compute-Intensive Functions Rest of Sequential 5% of Code CPU Code GPU CPU + GPUs : Two Year Heart Beat 32 Volta Stacked DRAM 16 Maxwell Unified Virtual Memory 8 Kepler Dynamic Parallelism 4 Fermi 2 FP64 DP GFLOPS GFLOPS per DP Watt 1 Tesla 0.5 CUDA 2008 2010 2012 2014 Kepler Features Make GPU Coding Easier Hyper-Q Dynamic Parallelism Speedup Legacy MPI Apps Less Back-Forth, Simpler Code FERMI 1 Work Queue CPU Fermi GPU CPU Kepler GPU KEPLER 32 Concurrent Work Queues Developer Momentum Continues to Grow 100M 430M CUDA –Capable GPUs CUDA-Capable GPUs 150K 1.6M CUDA Downloads CUDA Downloads 1 50 Supercomputer Supercomputers 60 640 University Courses University Courses 4,000 37,000 Academic Papers Academic Papers 2008 2013 Explosive Growth of GPU Accelerated Apps # of Apps Top Scientific Apps 200 61% Increase Molecular AMBER LAMMPS CHARMM NAMD Dynamics GROMACS DL_POLY 150 Quantum QMCPACK Gaussian 40% Increase Quantum Espresso NWChem Chemistry GAMESS-US VASP CAM-SE 100 Climate & COSMO NIM GEOS-5 Weather WRF Chroma GTS 50 Physics Denovo ENZO GTC MILC ANSYS Mechanical ANSYS Fluent 0 CAE MSC Nastran OpenFOAM 2010 2011 2012 SIMULIA Abaqus LS-DYNA Accelerated, In Development NVIDIA GPU Life Science Focus Molecular Dynamics: All codes are available AMBER, CHARMM, DESMOND, DL_POLY, GROMACS, LAMMPS, NAMD Great multi-GPU performance GPU codes: ACEMD, HOOMD-Blue Focus: scaling to large numbers of GPUs Quantum Chemistry: key codes ported or optimizing Active GPU acceleration projects: VASP, NWChem, Gaussian, GAMESS, ABINIT, Quantum Espresso, BigDFT, CP2K, GPAW, etc.
  • Modern Quantum Chemistry with [Open]Molcas

    Modern Quantum Chemistry with [Open]Molcas

    Modern quantum chemistry with [Open]Molcas Cite as: J. Chem. Phys. 152, 214117 (2020); https://doi.org/10.1063/5.0004835 Submitted: 17 February 2020 . Accepted: 11 May 2020 . Published Online: 05 June 2020 Francesco Aquilante , Jochen Autschbach , Alberto Baiardi , Stefano Battaglia , Veniamin A. Borin , Liviu F. Chibotaru , Irene Conti , Luca De Vico , Mickaël Delcey , Ignacio Fdez. Galván , Nicolas Ferré , Leon Freitag , Marco Garavelli , Xuejun Gong , Stefan Knecht , Ernst D. Larsson , Roland Lindh , Marcus Lundberg , Per Åke Malmqvist , Artur Nenov , Jesper Norell , Michael Odelius , Massimo Olivucci , Thomas B. Pedersen , Laura Pedraza-González , Quan M. Phung , Kristine Pierloot , Markus Reiher , Igor Schapiro , Javier Segarra-Martí , Francesco Segatta , Luis Seijo , Saumik Sen , Dumitru-Claudiu Sergentu , Christopher J. Stein , Liviu Ungur , Morgane Vacher , Alessio Valentini , and Valera Veryazov J. Chem. Phys. 152, 214117 (2020); https://doi.org/10.1063/5.0004835 152, 214117 © 2020 Author(s). The Journal ARTICLE of Chemical Physics scitation.org/journal/jcp Modern quantum chemistry with [Open]Molcas Cite as: J. Chem. Phys. 152, 214117 (2020); doi: 10.1063/5.0004835 Submitted: 17 February 2020 • Accepted: 11 May 2020 • Published Online: 5 June 2020 Francesco Aquilante,1,a) Jochen Autschbach,2,b) Alberto Baiardi,3,c) Stefano Battaglia,4,d) Veniamin A. Borin,5,e) Liviu F. Chibotaru,6,f) Irene Conti,7,g) Luca De Vico,8,h) Mickaël Delcey,9,i) Ignacio Fdez. Galván,4,j) Nicolas Ferré,10,k) Leon Freitag,3,l) Marco Garavelli,7,m) Xuejun Gong,11,n) Stefan Knecht,3,o) Ernst D. Larsson,12,p) Roland Lindh,4,q) Marcus Lundberg,9,r) Per Åke Malmqvist,12,s) Artur Nenov,7,t) Jesper Norell,13,u) Michael Odelius,13,v) Massimo Olivucci,8,14,w) Thomas B.
  • Dirac-Exact Relativistic Methods: the Normalized Elimination of the Small Component Method† Dieter Cremer,∗ Wenli Zou and Michael Filatov

    Dirac-Exact Relativistic Methods: the Normalized Elimination of the Small Component Method† Dieter Cremer,∗ Wenli Zou and Michael Filatov

    Advanced Review Dirac-exact relativistic methods: the normalized elimination of the small component method† Dieter Cremer,∗ Wenli Zou and Michael Filatov Dirac-exact relativistic methods, i.e., 2- or 1-component methods which exactly reproduce the one-electron energies of the original 4-component Dirac method, have established a standard for reliable relativistic quantum chemical calculations targeting medium- and large-sized molecules. Their development was initiated and facilitated in the late 1990s by Dyall’s development of the normalized elimination of the small component (NESC). Dyall’s work has fostered the conversion of NESC and related (later developed) methods into routinely used, multipurpose Dirac- exact methods by which energies, first-order, and second-order properties can be calculated at computational costs, which are only slightly higher than those of nonrelativistic methods. This review summarizes the development of a generally applicable 1-component NESC algorithm leading to the calculation of reliable energies, geometries, electron density distributions, electric moments, electric field gradients, hyperfine structure constants, contact densities and Mossbauer¨ isomer shifts, nuclear quadrupole coupling constants, vibrational frequencies, infrared intensities, and static electric dipole polarizabilities. In addition, the derivation and computational possibilities of 2-component NESC methods are discussed and their use for the calculation of spin-orbit coupling (SOC) effects in connection with spin-orbit splittings and SOC-corrected
  • Arxiv:1710.00259V1 [Physics.Chem-Ph] 30 Sep 2017 a Relativistically Correct Electron Interaction

    Arxiv:1710.00259V1 [Physics.Chem-Ph] 30 Sep 2017 a Relativistically Correct Electron Interaction

    One-step treatment of spin-orbit coupling and electron correlation in large active spaces Bastien Mussard1, ∗ and Sandeep Sharma1, y 1Department of Chemistry and Biochemistry, University of Colorado Boulder, Boulder, CO 80302, USA In this work we demonstrate that the heat bath configuration interaction (HCI) and its semis- tochastic extension can be used to treat relativistic effects and electron correlation on an equal footing in large active spaces to calculate the low energy spectrum of several systems including halogens group atoms (F, Cl, Br, I), coinage atoms (Cu, Au) and the Neptunyl(VI) dioxide radical. This work demonstrates that despite a significant increase in the size of the Hilbert space due to spin symmetry breaking by the spin-orbit coupling terms, HCI retains the ability to discard large parts of the low importance Hilbert space to deliver converged absolute and relative energies. For instance, by using just over 107 determinants we get converged excitation energies for Au atom in an active space containing (150o,25e) which has over 1030 determinants. We also investigate the accuracy of five different two-component relativistic Hamiltonians in which different levels of ap- proximations are made in deriving the one-electron and two-electrons Hamiltonians, ranging from Breit-Pauli (BP) to various flavors of exact two-component (X2C) theory. The relative accuracy of the different Hamiltonians are compared on systems that range in atomic number from first row atoms to actinides. I. INTRODUCTION can become large and it is more appropriate to treat them on an equal footing with the spin-free terms and electron Relativistic effects play an important role in a correlation.
  • Eigenvalues of the Breit Equation

    Eigenvalues of the Breit Equation

    Prog. Theor. Exp. Phys. 2013, 063B03 (13 pages) DOI: 10.1093/ptep/ptt041 Eigenvalues of the Breit equation Yoshio Yamaguchi1,† and Hikoya Kasari2,∗ 1Nishina Center, RIKEN, 350-0198 2-1 Hirosawa, Wako, Saitama, Japan 2Department of Physics, School of Science, Tokai University 259-1292 4-1-1 Kitakaname, Hiratsuka, Kanagawa, Japan ∗E-mail: [email protected] Received January 9, 2013; Accepted April 12, 2013; Published June 1, 2013 ............................................................................... Eigenvalues of the Breit equation Downloaded from e2 (α p + β m)αα δββ + δαα (−α p + β M)ββ − δαα δββ αβ = Eαβ , 1 1 2 2 r in which only the static Coulomb potential is considered, have been found. Here a detailed 1 discussion of the simple cases, S0, m = M, and m = M, is given, deriving the exact energy eigenvalues. An α2 expansion is used to find radial wave functions. The leading term is given by http://ptep.oxfordjournals.org/ the classical Coulomb wave function. The technique used here can be applied to other cases. ............................................................................... Subject Index B87 1. Introduction and the Breit equation at CERN LIBRARY on June 21, 2013 1.1. Introduction The Breit equation [1–3] has traditionally [4] been considered to be singular, and no attempt has ever been made to solve it. Instead, the Pauli approximation or a generalized Foldy–Wouthuysen trans- formation has been applied to derive the effective Hamiltonian Heff, consisting of the Schrödinger Hamiltonian 1 1 1 e2 H =− + p2 − 0 2 m M r and many other relativistic correction terms [4–6]. The perturbation method was then used to evaluate the eigenvalues (binding energies) in a power series with α as high as possible (or as high as necessary for experimental verification of quantum electrodynamics).