Operating Systems I
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Powershell Core Ja Sitä Edeltävät Komentorivi- Pohjaiset Hallintatyökalut
Ismail Belmostefa PowerShell Core ja sitä edeltävät komentorivi- pohjaiset hallintatyökalut Metropolia Ammattikorkeakoulu Insinööri (AMK) Tietotekniikan koulutusohjelma Insinöörityö 12.12.2016 Tiivistelmä Tekijä Ismail Belmostefa Otsikko PowerShell Core ja sitä edeltävät komentorivipohjaiset hallin- tatyökalut Sivumäärä 38 sivua + 2 liitettä Aika 12.12.2016 Tutkinto Insinööri (AMK) Koulutusohjelma Tietotekniikka Suuntautumisvaihtoehto Ohjelmistotekniikka Ohjaaja Kari Sundberg Ohjaajat Yliopettaja Markku Nuutinen Insinöörityön aiheena oli PowerShell Core ja sitä edeltävät komentorivipohjaiset hallinta- työkalut. Tavoite oli ymmärtää näiden asennusympäristö, alla käytetyt teknologiat ja niihin liittyvä terminologia. Tutkimustyö syntyi harjoittelutyön muistiinpanojen lopputuloksena sekä tutkimalla alan kirjallisuutta ja verkkomateriaalia. Insinöörityössä selvitettiin PowerShell Coren ja sitä edeltävien komentorivipohjaisten hal- lintatyökalujen alla käytetyt teknologiat, terminologia, käyttökohteet ja motivaatio niiden syntyyn. Koska komentorivipohjaiset hallintatyökalut on rakennettu asennusympäristön tar- joamien palveluiden päälle, palveluiden toiminnan hahmottaminen edesauttaa komentori- vin käyttöä ja soveltamista. Tutkimustyötä on hyödynnetty tietokoneen ylläpidossa, ohjel- moinnissa ja peruskäytössä. Tutkimustyö osoitti asennusympäristön kokonaiskuvan hallit- semisen tärkeyden komentorivipohjaisten työkalujen käytössä. Avainsanat DDE, OLE, COM, .NET, CMD.EXE, COMMAND.COM, WSH, MOM, PowerShell Abstract Author Ismail Belmostefa Title -

Automated Testing of Firmware Installation and Update Scenarios for Peripheral Devices
DEGREE PROJECT IN COMPUTER SCIENCE AND ENGINEERING, SECOND CYCLE, 30 CREDITS STOCKHOLM, SWEDEN 2019 Automated testing of firmware installation and update scenarios for peripheral devices DAG REUTERSKIÖLD KTH ROYAL INSTITUTE OF TECHNOLOGY SCHOOL OF ELECTRICAL ENGINEERING AND COMPUTER SCIENCE Automated testing of firmware installation and update scenarios for peripheral devices DAG REUTERSKIÖLD Master in Computer Science Date: August 12, 2019 Supervisor: Hamid Faragardi Examiner: Elena Troubitsyna School of Electrical Engineering and Computer Science Host company: Tobii AB Swedish title: Automatisering av enhetsinstallation, uppdatering och testning med hjälp av virtuella maskiner iii Abstract This research presents an approach to transition from manual to automated testing of hardware specific firmware. The manual approach for firmware test- ing can be repetitive and time consuming. A significant proportion of the time is spent on cleaning and re-installing operating systems so that old firmware does not interfere with the newer firmware that is being tested. The approach in this research utilizes virtual machines and presents an automation framework. One component of the automation framework is an application to imitate con- nected peripheral devices to bypass hardware dependencies of firmware in- stallers. The framework also consists of automation and pipeline scripts with the objective to execute firmware installers and detect errors and abnormalities in the installation and updating processes. The framework can run on locally hosted virtual machines, but is most applicable using cloud hosted virtual ma- chines, where it is part of a continuous integration that builds, downloads, installs, updates and tests new firmware versions, in a completely automated manner. The framework is evaluated by measuring and comparing execution times with manually conducted installation and updating tests, and the result shows that the framework complete tests much faster than the manual approach. -

Open WATCOM Programmer's Guide
this document downloaded from... Use of this document the wings of subject to the terms and conditions as flight in an age stated on the website. of adventure for more downloads visit our other sites Positive Infinity and vulcanhammer.net chet-aero.com Watcom FORTRAN 77 Programmer's Guide Version 1.8 Notice of Copyright Copyright 2002-2008 the Open Watcom Contributors. Portions Copyright 1984-2002 Sybase, Inc. and its subsidiaries. All rights reserved. Any part of this publication may be reproduced, transmitted, or translated in any form or by any means, electronic, mechanical, manual, optical, or otherwise, without the prior written permission of anyone. For more information please visit http://www.openwatcom.org/ Portions of this manual are reprinted with permission from Tenberry Software, Inc. ii Preface The Watcom FORTRAN 77 Programmer's Guide includes the following major components: · DOS Programming Guide · The DOS/4GW DOS Extender · Windows 3.x Programming Guide · Windows NT Programming Guide · OS/2 Programming Guide · Novell NLM Programming Guide · Mixed Language Programming · Common Problems Acknowledgements This book was produced with the Watcom GML electronic publishing system, a software tool developed by WATCOM. In this system, writers use an ASCII text editor to create source files containing text annotated with tags. These tags label the structural elements of the document, such as chapters, sections, paragraphs, and lists. The Watcom GML software, which runs on a variety of operating systems, interprets the tags to format the text into a form such as you see here. Writers can produce output for a variety of printers, including laser printers, using separately specified layout directives for such things as font selection, column width and height, number of columns, etc. -

Virtual MBX Driver Help
Virtual MBX Driver Help Virtual MBX Driver for Modbus, Modbus Plus and Modbus TCP Networks Version 9 Virtual MBX Driver Help VIRTUAL MBX DRIVER HELP Virtual MBX® Driver for Modbus, Modbus Plus and Modbus TCP Networks Version 9 Copyright © 1994-2017, Cyberlogic® Technologies Inc. All rights reserved. This document and its contents are protected by all applicable copyright, trademark and patent laws and international treaties. No part of this document may be copied, reproduced, stored in a retrieval system or transmitted by any means, electronic, mechanical, photocopying, recording or otherwise, without the express written permission of Cyberlogic Technologies Inc. This document is subject to change without notice, and does not necessarily reflect all aspects of the mentioned products or services, their performance or applications. Cyberlogic Technologies Inc. is not responsible for any errors or omissions in this presentation. Cyberlogic Technologies Inc. makes no express or implied warranties or representations with respect to the contents of this document. No copyright, trademark or patent liability or other liability for any damages is assumed by Cyberlogic Technologies Inc. with respect to the use of the information contained herein by any other party. Cyberlogic®, DHX®, MBX®, WinConX® and Intelligent • Powerful • Reliable® are registered trademarks and DirectAccess™, OPC Crosslink™, OPC Datacenter™, DevNet™ and C-logic™ are trademarks of Cyberlogic Technologies Inc. All other trademarks and registered trademarks belong to their respective -

Windows 2000 Professional Basics
PART I Windows 2000 Professional Basics Learn To: • Install Windows 2000 Professional • Install and organize COPYRIGHTEDremove MATERIAL programs • Add a local and a network printer CHAPTER 1 Introducing Windows 2000 Professional FEATURING: Windows 2000 Professional, Windows 2000 Server: Which is which? 4 What’s new in Windows 2000 Professional? 8 What’s not in Windows 2000 Professional? 16 Why choose Windows 2000 Professional over Windows 98? 17 How is Windows 2000 Professional different from other operating systems? 25 What are the features of Windows 2000 Professional architecture? 27 Weaknesses of Windows 2000 Professional 31 Since the advent of the personal computer, users have wanted three things in an operating system: power, stability, and usability. Windows 2000 Professional has all these and more in abundance. Since its inception in 1993, Windows NT has featured an indefatigable 32-bit architecture, complete with built-in networking and the capa- bility to run almost every piece of Windows software on the market. Windows 2000 Professional now includes an interface, which has evolved from the NT 4 Explorer shell and is even easier to use. NOTE Windows 2000 Professional is actually version 5 of Windows NT Workstation. Throughout the book, I make many references to NT in describing Windows 2000. The name change was a sign of the convergence of the Windows product lines. What does all this mean to the consumer, the person sitting at a desk 52 weeks a year who just wants to be a productive computer user? It means a lot. It means a fast, up-to-date operating system with a slew of advanced features that ensure the computer will almost never crash. -

L38 Ñ Windows XP
History History (cont.) (Timeline from www.cgonline.com) 10/81 — IBM PC (“Personal Computer”) 10/88 — OS/2 1.1 (Windows-like GUI, end and PC-DOS 1.0 of collaboration when IBM gets upset with Microsoft for improving Windows) 3/83 — Microsoft MS-DOS 2.0 (hard disk, file system) 5/90 — Windows 3.0 (big success!) 11/83 — Windows announced (vaporware!) 4/92 — Windows 3.1 (bug fixes etc.) 11/84 — MS-DOS 3.1 10/92 — Windows for Workgroups 3.1 (adds networking, but fails in market) 11/85 — Windows 1.0 (tiled windows, doesn’t do well in market) 5/93 — Windows NT 3.1 (visually like Windows 3.1, but stable 32-bit platform) 4/87 — IBM & Microsoft OS/2 1.0 (next generation, DOS-like command lines) 11/93 — Windows for Workgroups 3.11 (precursor to Windows 95) 12/87 — Windows/386 (uses 80386’s virtual memory to allow safe “preemptive” 5/94 — MS-DOS 6.22 (DOS final version) multitasking) 9/94 — Windows NT 3.5 6/95 — Windows NT 3.51 (faster) 1 Fall 2002, Lecture 38 2 Fall 2002, Lecture 38 History (cont.) What is Windows XP? 8/95 — Windows 95 (originally Windows I 32/64 -bit preemptive multitasking 4.0) (long file names, plug and play operating system for AMD K6/7, Intel hardware, taskbar and Start menu, IA32/64 and later microprocessors HUGE success in market!) ● Replaces Windows 95/98/Me as well as Windows NT/200 7/96 — Windows NT 4.0 (Windows 95 GUI, first successful version of NT) I Key goals 6/98 — Windows 98 (Windows 95 + ● security, reliability, ease of use Internet Explorer 4.0, success in market) ● Windows and POSIX compliance ● high performance, extensibility 2/00 — Windows 2000 (Windows NT 4.0 + plug and play, DirectX, USB, etc.) ● portability, international support 9/00 — Windows Me (Millennium Edition) I Various versions: XP Personal, XP (Windows 98 + IE 5.0, media support, Professional, XP Server last version in Windows 9x line) I Uses a micro-kernel architecture 9/01 — Windows XP (combines Windows ● Subsystems to provide OS personalities 2000 and ME, but based on NT/2000) for Win32, POSIX, etc. -
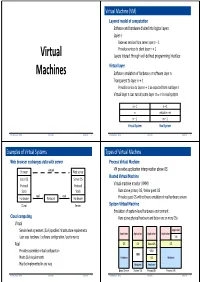
Virtual Machines Dr
Virtual Machine (VM) Layered model of computation Software and hardware divided into logical layers Layer n Receives services from server layer n – 1 Provides services to client layer n + 1 Virtual Layers interact through well-defined programming interface Virtual layer Machines Software emulation of hardware or software layer n Transparent to layer n + 1 Provides service to layer n + 1 as expected from real layer n Virtual layer n can run at some layer m ≠ n in real system n + 1 n + 1 n virtual n = m n –1 m –1 Virtual System Real System Modern Microprocessors — Fall 2012 Virtual Machines Dr. Martin Land 1 Modern Microprocessors — Fall 2012 Virtual Machines Dr. Martin Land 2 Examples of Virtual Systems Types of Virtual Machine Web browser exchanges data with server Process Virtual Machine VM provides application interpretation above OS Browser virtual Web server Hosted Virtual Machine Local OS Server OS Protocol Protocol Virtual machine monitor (VMM) Stack Stack Runs above primary OS / below guest OS real real Hardware Network Hardware Provides guest OS with software emulation of real hardware system Client Server System Virtual Machine Emulation of system-level hardware environment Cloud computing Runs above physical hardware and below one or more OSs Virtual Service level agreement (SLA) specifies infrastructure requirements Application Application Application Application Application User sees hardware / software configuration / performance VM Real OS OS Guest OS OS Provider assembles virtual configuration VMM VMM Meets SLA requirements Hardware OS Hardware May be implemented in any way Hardware Hardware Basic System System VM Hosted VM Process VM Modern Microprocessors — Fall 2012 Virtual Machines Dr. -

L38 Ñ Windows 2000
History History (cont.) (Timeline from www.cgonline.com) 10/81 — IBM PC (“Personal Computer”) 10/88 — OS/2 1.1 (Windows-like GUI, end and PC-DOS 1.0 of collaboration when IBM gets upset with Microsoft for improving Windows) 3/83 — Microsoft MS-DOS 2.0 (hard disk, file system) 5/90 — Windows 3.0 (big success!) 11/83 — Windows announced (vaporware!) 4/92 — Windows 3.1 (bug fixes etc.) 11/84 — MS-DOS 3.1 10/92 — Windows for Workgroups 3.1 (adds networking, but fails in market) 11/85 — Windows 1.0 (tiled windows, doesn’t do well in market) 5/93 — Windows NT 3.1 (visually like Windows 3.1, but stable 32-bit platform) 4/87 — IBM & Microsoft OS/2 1.0 (next generation, DOS-like command lines) 11/93 — Windows for Workgroups 3.11 (precursor to Windows 95) 12/87 — Windows/386 (uses 80386’s virtual memory to allow safe “preemptive” 5/94 — MS-DOS 6.22 (DOS final version) multitasking) 9/94 — Windows NT 3.5 6/95 — Windows NT 3.51 (faster) 1 Fall 2001, Lecture 38 2 Fall 2001, Lecture 38 History (cont.) What is Windows 2000? 8/95 — Windows 95 (originally Windows n 32-bit preemptive multitasking operating 4.0) (long file names, plug and play system for Intel microprocessors hardware, taskbar and Start menu, HUGE success in market!) n Key goals ● extensibility 7/96 — Windows NT 4.0 (Windows 95 GUI, first successful version of NT) ● portability ● reliability 6/98 — Windows 98 (Windows 95 + ● POSIX compliance & compatibility with Internet Explorer 4.0, success in market) MS-DOS and MS-Windows applications 2/00 — Windows 2000 (Windows NT 4.0 + ● performance -

Copyrighted Material
38400bindex.fm Page 643 Monday, December 17, 2007 10:22 PM Index Note to the reader: Throughout this index boldfaced page numbers indicate primary discussions of a topic. Ital- icized page numbers indicate illustrations. Symbols and Numbers obtaining user's logon name, 486 pipe for data transfer between utilities, 480 * (asterisk) test server for, 488 DSQuery utility for all objects, 484 Active Directory Application Mode, 4 in regular expressions, 407 Active Directory Lightweight Directory Services (AD in script for password, 488 LDS), 4 as wildcard character, 359 Active Directory Services Interface Editor (ADSIEdit), ^ (circumflex), in regular expressions, 407 468 $ (dollar sign), in regular expressions, 407 active route, 309 $username$ token, 471 Active Server Pages (ASP), 5, 551 > (greater than) sign, for output redirection, 380 installing support in IIS, 556, 556 < (less than) sign, for input redirection, 381 active session, disconnecting, with TSDiscon utility, . (period), in regular expressions, 407 436–437 ? (question mark) ActiveXObject() method, 185 in AppCmd utility, 561 activity indicator, 344 as wildcard character, 359 ADAP utility, 65 /? (command line switch), 587 ADD command (AppCmd), 571, 572 for help, 23–25, 616 add command (NetSH), 170 script code to handle, 185–186 ADD command (Route utility), 310 / (slash), for command line switch, 23–24 add disk command (DiskPart), 229 [ ] (square brackets) Add to Favorites dialog box (RegEdit), 71 for optional command input, 23 AddPrinterConnection() method, of WshNetwork object, -

Windows 2000
AppendixC Windows 2000 The Microsoft Windows operating system is a 32-bit preemptive multitasking operating system for Intel Pentium and later microprocessors. The successor to the Windows NT operating system, it was previously named Windows NT Version 5.0. Key goals for the system are portability, security, Portable Oper- ating System Interface (POSIX or IEEE Std. 1003.1) compliance, multiprocessor support, extensibility, international support, and compatibility with MS-DOS and Microsoft Windows applications. In this appendix, we discuss the key goals for this system, the layered architecture of the system that makes it so easy to use, the file system, networks, and the programming interface. C.1 History In the mid-1980s, Microsoft and IBM cooperated to develop the OS/2 operating system, which was written in assembly language for single-processor Intel 80286 systems. In 1988, Microsoft decided to make a fresh start and to develop a “new technology” (or NT) portable operating system that supported both the OS/2 and POSIX application programming interfaces (APIs). In October 1988, Dave Cutler, the architect of the DEC VAX/VMS operating system, was hired and given the charter of building this new operating system. Originally, the team planned for NT to use the OS/2 API as its native environment, but during development, it was changed to use the 32-bit Windows API (or Win32 API), reflecting the popularity of Windows 3.0.The first versions of NT were Windows NT 3.1 and Windows NT 3.1 Advanced Server. (At that time, 16-bit Windows was at Version 3.1.) Windows NT 4.0 adopted the Windows 95 user interface and incorporated Internet web-server and web-browser software. -
![2.3 Win-Personalities [Read-Only]](https://docslib.b-cdn.net/cover/5232/2-3-win-personalities-read-only-4915232.webp)
2.3 Win-Personalities [Read-Only]
Unit OS2: Operating System Principles 2.3. Windows on Windows - OS Personalities Windows Operating System Internals - by David A. Solomon and Mark E. Russinovich with Andreas Polze Copyright Notice © 2000-2005 David A. Solomon and Mark Russinovich These materials are part of the Windows Operating System Internals Curriculum Development Kit, developed by David A. Solomon and Mark E. Russinovich with Andreas Polze Microsoft has licensed these materials from David Solomon Expert Seminars, Inc. for distribution to academic organizations solely for use in academic environments (and not for commercial use) 2 1 Roadmap for Section 2.3. Environment Subsystems System Service Dispatching Windows on Windows - 16bit Windows on Windows - 64bit 3 Multiple OS Personalities Environment Subsystems System User & Service Application POSIX Processes OS/2 Windows User Subsystem DLL Windows Mode Kernel Mode Executive Windows Device Drivers Kernel User/GDI Hardware Abstraction Layer (HAL) Device Driver 4 2 What about .NET and WinFX? WinFX is the .NET Framework that will ship with Longhorn Both .NET and WinFX are built on standard Windows APIs They are not a subsystem They do not call undocumented NT system calls .NET/WinFX Application .NET/WinFXFramework User Windows API DLLs Mode Kernel Windows Kernel Mode 5 Environment Subsystems Environment subsystems provide exposed, documented interface between application and NT native API Each subsystem defines a different set of APIs & semantics Subsystems implement these by invoking native APIs i.e., subsystem “wraps” -

User Guide for Version 3.3
User Guide for version 3.3 Contents CONVENTIONS AND TERMS .......................................................2 WHAT’S NEW SINCE VERSION 2?...............................................2 COMPATIBILITY ..............................................................................2 INSTALLATION ................................................................................2 ABOUT MO’SLO DELUXE..............................................................3 ABOUT COMMAND LINES ............................................................3 TELLING MO’SLO DELUXE WHAT TO SLOW ..........................4 Parameters for Slowed Programs ...........................................4 Slowing a Command Prompt..................................................4 TELLING MO’SLO DELUXE HOW MUCH TO SLOW...............4 Percent-of-system-speed .........................................................4 Processor Emulation ...............................................................5 DISABLING THE LEVEL 1 CACHE ..............................................5 SLOWDOWN METHODS................................................................6 DELAYING SLOWDOWN AND LIMITING DURATION...........6 DISABLING THE COM PORT FIFO BUFFER.............................6 KEYBOARD CONTROL AND QUICKLOAD...............................7 TERMINATE BUT STAY RESIDENT.............................................7 ABOUT WINDOWS SHORTCUTS.................................................8 CREATING A DESKTOP SHORTCUT..........................................8 ADDING SLOWDOWN TO SHORTCUT