DOCSLIB.ORG

02 Stationary Time Series

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
02 Stationary Time Series 02 Stationary time series Andrius Buteikis, [email protected] http://web.vu.lt/mif/a.buteikis/ Introduction All time series may be divided into two big classes - stationary and non-stationary. I Stationary process - a random process with a constant mean, variance and covariance. Examples of stationary time series: WN, mean = 0 MA(3), mean = 5 AR(1), mean = 5 2 7 8 6 1 6 5 x1 x2 x3 0 4 4 −1 3 2 2 −2 0 50 100 150 200 0 50 100 150 200 0 50 100 150 200 Time Time Time The three example processes fluctuate around their constant mean values. Looking from the graphs, the fluctuations of the first two graphs seem to be constant, however the third one is not so apparent. If we plot the last time series for a longer time period: AR(1), mean = 5 8 6 x3 4 2 0 50 100 150 200 Time AR(1), mean = 5 8 6 x3 4 2 0 100 200 300 400 Time We can see that the fluctuations are indeed around a constant mean and the variance does not appear to change throughout the period. Some non-stationary time series examples: I Yt = t + t , where t ∼ N (0, 1); 2 I Yt = t · t, where t ∼ N (0, σ ); Pt I Yt = j=1 Zj , where each independent variable Zj is either 1 or −1, with a 50% probability for either value. The reasons for their non-stationarity are as follows: I The first time series is not stationary because its mean is not constant: EYt = t - depends on t; I The second time series is not stationary because its variance is not 2 2 constant: Var(Yt ) = t · σ - depends on t. However, EYt = 0 · t = 0 is constant; I The third time series is not stationary because even though Pt EYt = j=1 (0.5 + (−0.5)) = 0, the variance 2 2 2 Var(Yt ) = E(Yt ) − (E(Yt )) = E(Yt ) = t where: 2 Pt 2 P 2 E(Yt ) = j=1 E(Zj ) + 2 j6=k E(Zj Zk ) = t · (0.5 · 1 + 0.5 · (−1) ) = t The sample data graphs are provided below: non stationary in mean non stationary in variance no clear tendency 50 4 100 3 40 2 50 30 1 ns1 ns2 ns3 0 20 0 −1 10 −2 −50 0 −3 0 10 20 30 40 50 0 10 20 30 40 50 0 10 20 30 40 50 Index Index Index I White noise (WN) - a stationary process of uncorrelated (sometimes we may demand a stronger property of independence) random variables with zero mean and constant variance. White noise is a model of an absolutely chaotic process of uncorrelated observations - it is a process that immediately forgets its past. How can we know which of the previous three stationary graphs are not WN? Two functions help us determine this: I ACF - Autocorrelation function I PACF - Partial autocorrelation function If all the bars (except the 0th in the ACF) are within the blue band - the stationary process is WN. WN MA(3) AR(1) 1.0 0.8 0.8 0.6 0.4 0.4 ACF ACF ACF 0.2 0.0 0.0 −0.2 0 5 10 15 20 0 5 10 15 20 0 5 10 15 20 25 Lag Lag Lag WN MA(3) AR(1) 0.10 0.6 0.3 0.4 0.00 0.1 0.2 Partial ACF Partial ACF Partial ACF 0.0 −0.10 −0.1 5 10 15 20 5 10 15 20 0 5 10 15 20 25 Lag Lag Lag The 95% confidence intervals are calculated from: qnorm(p = c(0.025, 0.975))/sqrt(n) (more details on the confidence interval calculation are provided later in these slides) par(mfrow = c(1,2)) set.seed(10) n = 50 x0 <- rnorm(n) acf(x0) abline(h = qnorm(c(0.025, 0.975))/sqrt(n), col = "red") pacf(x0) abline(h = qnorm(c(0.025, 0.975))/sqrt(n), col = "red") Series x0 Series x0 0.3 1.0 0.8 0.2 0.6 0.1 0.4 0.0 ACF Partial ACF 0.2 −0.1 0.0 −0.2 −0.2 0 5 10 15 5 10 15 Lag Lag To decide whether a time series is stationary, examine its graph. To decide whether a stationary time series is WN, examine its ACF and PACF. Covariance-Stationary Time Series I In cross-sectional data different observations were assumed to be uncorrelated; I In time series we require that there be some dynamics, some persistence, some way in which the present is linked to the past and the future - to the present. Having historical data then would allow us to forecast the future. If we want to forecast a series - at a minimum we would like its mean and covariance structure to be stable over time. In that case, we would say that the series is covariance stationary. There are two requirements for this to be true: 1. The mean of the series is stable over time: EYt = µ; 2. The covariance structure is stable over time. In general, the (auto)covariance between Yt and Yt−τ is: γ(t, τ) = cov(Yt , Yt−τ ) = E(Yt − µ)(Yt−τ − µ) If the covariance structure is stable, then the covariance depends on τ but not on t: γ(t, τ) = γ(τ). Note: γ(0) = Cov(Yt , Yt ) = Var(Yt ) < ∞. Remark When observing/measuring time series we obtain numbers y1, ..., yT which are the realization of random variables Y1, ..., YT . Using probabilistic concepts, we can give a more precise definition of a (weak) stationary series: I If EYt = µ - the process is called mean-stationary; 2 I If Var(Yt ) = σ < ∞ - the process is called variance-stationary; I If γ(t, τ) = γ(τ) - the process is called covariance-stationary. In other words, a time series Yt is stationary if its mean, variance and covariance do not depend on t. If at least one of the three requirements is not met, then the process is not-stationary. Since we often work with the (auto)correlation between Yt and Yt−τ rather than the (auto)covariance (because they are easier to interpret), we can calculate the autocorrelation function (ACF): cov(Yt , Yt−τ ) γ(τ) ρ(τ) = p = Var(Yt )Var(Yt−τ ) γ(0) Note: ρ(0) = 1, |ρ(τ)| ≤ 1. The partial autocorrelation function (PACF) measures the association between Yt and Yt−k : p(k) = βk , where Yt = α + β1Yt−1 + ... + βk Yt−k + t The variance of the autocorrelation coefficient at lag k, rk , is normally distributed at the limit, and the variance can be approximated: 1 Var(r ) ∼ (where T is the number of observations). k T As such, we want to create lower and upper 95% confidence bounds for 1 1 the normal distribution N 0, , whose standard deviation is √ . T T The 95% confidence interval (of a stationary time series) is: 1.96 ∆ = 0 ± √ T In general, the critical value of a standard normal distribution and its confidence interval can be found in these steps: 1 − Q Compute α = , where Q is the confidence level; I 2 I To express the critical value as a z − score, find the z1−α value. For example, if Q = 0.95, then α = 0.05. Then, the standard normal distributions 1 − α quantile is z0.025 ≈ 1.96. White Noise White noise processes are the fundamental building blocks of all stationary time series. 2 We denote it t ∼ WN(0, σ ) - a zero mean, constant variance and serially uncorrelated (ρ(t, τ) = 0, for τ > 0 and any t) random variable process. Sometimes we demand a stronger property of independence. From the definition it follows that: I E(t ) = 0; 2 I Var(t ) = σ < ∞; I γ(t, τ) = E(t − Et )(t−τ − Et−τ ) = E(t t−τ ), where: ( 0, if τ 6= 0 E(t t−τ ) = σ2, if τ = 0 Example on how to check if a process is stationary. 2 Let us check if Yt = t + β1t−1, where t ∼ WN(0, σ ) is stationary: 1. EYt = E(t + β1t−1) = 0 + β1 · 0 = 0; 2 2 2 2 2. Var(Yr ) = Var(t + β1t−1) = σ + β1 σ = σ (1 + β1); 3. The autocovariance for τ > 0: γ(t, τ) = E(Yt Yt−τ ) = E(t + β1t−1)(t−τ + β1t−τ−1) 2 = Et t−τ + β1Et t−τ−1 + β1Et−1t−τ + β1 Et−1t−τ−1 ( 2 β1σ , if τ = 1 = β1Et−1t−τ = 0, if τ > 1 None of these characteristics depend on t, which means that the process is stationary. This process has a very short memory (i.e. if Yt and Yt+τ are separated by more than one time period - they are uncorrelated). On the other hand, this process is not a WN. The Lag Operator The lag operator L is used to lag a time series: LYt = Yt−1. Similarly: 2 L Yt = L(LYt ) = L(Yt−1) = Yt−2 etc. In general, we can write: p L Yt = Yt−p Typically, we operate on a time series with a polynomial in the lag operator. A lag operator polynomial of degree m is: 2 m B(L) = β0 + β1L + β2L + ... + βmL For example, if B(L) = 1 + 0.9L − 0.6L2, then: B(L)Yt = Yt + 0.9Yt−1 − 0.6Yt−2 A well known operator - the first-difference operator ∆ - is a first-order polynomial in the lag operator: ∆Yt = Yt − Yt−1 = (1 − L)Yt , i.e.
Load more

Recommended publications
  • Stationary Processes and Their Statistical Properties
    Stationary Processes and Their Statistical Properties Brian Borchers March 29, 2001 1 Stationary processes A discrete time stochastic process is a sequence of random variables Z1, Z2, :::. In practice we will typically analyze a single realization z1, z2, :::, zn of the stochastic process and attempt to esimate the statistical properties of the stochastic process from the realization. We will also consider the problem of predicting zn+1 from the previous elements of the sequence. We will begin by focusing on the very important class of stationary stochas- tic processes. A stochastic process is strictly stationary if its statistical prop- erties are unaffected by shifting the stochastic process in time. In particular, this means that if we take a subsequence Zk+1, :::, Zk+m, then the joint distribution of the m random variables will be the same no matter what k is. Stationarity requires that the mean of the stochastic process be a constant. E[Zk] = µ. and that the variance is constant 2 V ar[Zk] = σZ : Also, stationarity requires that the covariance of two elements separated by a distance m is constant. That is, Cov(Zk;Zk+m) is constant. This covariance is called the autocovariance at lag m, and we will use the notation γm. Since Cov(Zk;Zk+m) = Cov(Zk+m;Zk), we need only find γm for m 0. The ≥ correlation of Zk and Zk+m is the autocorrelation at lag m. We will use the notation ρm for the autocorrelation. It is easy to show that γk ρk = : γ0 1 2 The autocovariance and autocorrelation ma- trices The covariance matrix for the random variables Z1, :::, Zn is called an auto- covariance matrix.
    [Show full text]
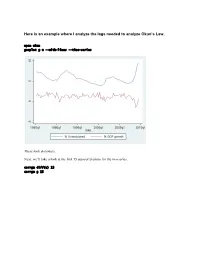
  • Here Is an Example Where I Analyze the Lags Needed to Analyze Okun's
    Here is an example where I analyze the lags needed to analyze Okun’s Law. open okun gnuplot g u --with-lines --time-series These look stationary. Next, we’ll take a look at the first 15 autocorrelations for the two series. corrgm diff(u) 15 corrgm g 15 These are autocorrelated and so are these. I would expect that a simple regression will not be sufficient to model this relationship. Let’s try anyway. Run a simple regression and look at the residuals ols diff(u) const g series ehat=$uhat gnuplot ehat --with-lines --time-series These look positively autocorrelated to me. Notice how the residuals fall below zero for a while, then rise above for a while, and repeat this pattern. Take a look at the correlogram. The first autocorrelation is significant. More lags of D.u or g will probably fix this. LM test of residuals smpl 1985.2 2009.3 ols diff(u) const g modeltab add modtest 1 --autocorr --quiet modtest 2 --autocorr --quiet modtest 3 --autocorr --quiet modtest 4 --autocorr --quiet Breusch-Godfrey test for first-order autocorrelation Alternative statistic: TR^2 = 6.576105, with p-value = P(Chi-square(1) > 6.5761) = 0.0103 Breusch-Godfrey test for autocorrelation up to order 2 Alternative statistic: TR^2 = 7.922218, with p-value = P(Chi-square(2) > 7.92222) = 0.019 Breusch-Godfrey test for autocorrelation up to order 3 Alternative statistic: TR^2 = 11.200978, with p-value = P(Chi-square(3) > 11.201) = 0.0107 Breusch-Godfrey test for autocorrelation up to order 4 Alternative statistic: TR^2 = 11.220956, with p-value = P(Chi-square(4) > 11.221) = 0.0242 Yep, that’s not too good.
    [Show full text]
  • Methods of Monte Carlo Simulation II
    Methods of Monte Carlo Simulation II Ulm University Institute of Stochastics Lecture Notes Dr. Tim Brereton Summer Term 2014 Ulm, 2014 2 Contents 1 SomeSimpleStochasticProcesses 7 1.1 StochasticProcesses . 7 1.2 RandomWalks .......................... 7 1.2.1 BernoulliProcesses . 7 1.2.2 RandomWalks ...................... 10 1.2.3 ProbabilitiesofRandomWalks . 13 1.2.4 Distribution of Xn .................... 13 1.2.5 FirstPassageTime . 14 2 Estimators 17 2.1 Bias, Variance, the Central Limit Theorem and Mean Square Error................................ 19 2.2 Non-AsymptoticErrorBounds. 22 2.3 Big O and Little o Notation ................... 23 3 Markov Chains 25 3.1 SimulatingMarkovChains . 28 3.1.1 Drawing from a Discrete Uniform Distribution . 28 3.1.2 Drawing From A Discrete Distribution on a Small State Space ........................... 28 3.1.3 SimulatingaMarkovChain . 28 3.2 Communication .......................... 29 3.3 TheStrongMarkovProperty . 30 3.4 RecurrenceandTransience . 31 3.4.1 RecurrenceofRandomWalks . 33 3.5 InvariantDistributions . 34 3.6 LimitingDistribution. 36 3.7 Reversibility............................ 37 4 The Poisson Process 39 4.1 Point Processes on [0, )..................... 39 ∞ 3 4 CONTENTS 4.2 PoissonProcess .......................... 41 4.2.1 Order Statistics and the Distribution of Arrival Times 44 4.2.2 DistributionofArrivalTimes . 45 4.3 SimulatingPoissonProcesses. 46 4.3.1 Using the Infinitesimal Definition to Simulate Approx- imately .......................... 46 4.3.2 SimulatingtheArrivalTimes . 47 4.3.3 SimulatingtheInter-ArrivalTimes . 48 4.4 InhomogenousPoissonProcesses. 48 4.5 Simulating an Inhomogenous Poisson Process . 49 4.5.1 Acceptance-Rejection. 49 4.5.2 Infinitesimal Approach (Approximate) . 50 4.6 CompoundPoissonProcesses . 51 5 ContinuousTimeMarkovChains 53 5.1 TransitionFunction. 53 5.2 InfinitesimalGenerator . 54 5.3 ContinuousTimeMarkovChains .
    [Show full text]
  • Examples of Stationary Time Series
    Statistics 910, #2 1 Examples of Stationary Time Series Overview 1. Stationarity 2. Linear processes 3. Cyclic models 4. Nonlinear models Stationarity Strict stationarity (Defn 1.6) Probability distribution of the stochastic process fXtgis invariant under a shift in time, P (Xt1 ≤ x1;Xt2 ≤ x2;:::;Xtk ≤ xk) = F (xt1 ; xt2 ; : : : ; xtk ) = F (xh+t1 ; xh+t2 ; : : : ; xh+tk ) = P (Xh+t1 ≤ x1;Xh+t2 ≤ x2;:::;Xh+tk ≤ xk) for any time shift h and xj. Weak stationarity (Defn 1.7) (aka, second-order stationarity) The mean and autocovariance of the stochastic process are finite and invariant under a shift in time, E Xt = µt = µ Cov(Xt;Xs) = E (Xt−µt)(Xs−µs) = γ(t; s) = γ(t−s) The separation rather than location in time matters. Equivalence If the process is Gaussian with finite second moments, then weak stationarity is equivalent to strong stationarity. Strict stationar- ity implies weak stationarity only if the necessary moments exist. Relevance Stationarity matters because it provides a framework in which averaging makes sense. Unless properties like the mean and covariance are either fixed or \evolve" in a known manner, we cannot average the observed data. What operations produce a stationary process? Can we recognize/identify these in data? Statistics 910, #2 2 Moving Average White noise Sequence of uncorrelated random variables with finite vari- ance, ( 2 often often σw = 1 if t = s; E Wt = µ = 0 Cov(Wt;Ws) = 0 otherwise The input component (fXtg in what follows) is often modeled as white noise. Strict white noise replaces uncorrelated by independent. Moving average A stochastic process formed by taking a weighted average of another time series, often formed from white noise.
    [Show full text]
  • Alternative Tests for Time Series Dependence Based on Autocorrelation Coefficients
    Alternative Tests for Time Series Dependence Based on Autocorrelation Coefficients Richard M. Levich and Rosario C. Rizzo * Current Draft: December 1998 Abstract: When autocorrelation is small, existing statistical techniques may not be powerful enough to reject the hypothesis that a series is free of autocorrelation. We propose two new and simple statistical tests (RHO and PHI) based on the unweighted sum of autocorrelation and partial autocorrelation coefficients. We analyze a set of simulated data to show the higher power of RHO and PHI in comparison to conventional tests for autocorrelation, especially in the presence of small but persistent autocorrelation. We show an application of our tests to data on currency futures to demonstrate their practical use. Finally, we indicate how our methodology could be used for a new class of time series models (the Generalized Autoregressive, or GAR models) that take into account the presence of small but persistent autocorrelation. _______________________________________________________________ An earlier version of this paper was presented at the Symposium on Global Integration and Competition, sponsored by the Center for Japan-U.S. Business and Economic Studies, Stern School of Business, New York University, March 27-28, 1997. We thank Paul Samuelson and the other participants at that conference for useful comments. * Stern School of Business, New York University and Research Department, Bank of Italy, respectively. 1 1. Introduction Economic time series are often characterized by positive
    [Show full text]
  • 3 Autocorrelation
    3 Autocorrelation Autocorrelation refers to the correlation of a time series with its own past and future values. Autocorrelation is also sometimes called “lagged correlation” or “serial correlation”, which refers to the correlation between members of a series of numbers arranged in time. Positive autocorrelation might be considered a specific form of “persistence”, a tendency for a system to remain in the same state from one observation to the next. For example, the likelihood of tomorrow being rainy is greater if today is rainy than if today is dry. Geophysical time series are frequently autocorrelated because of inertia or carryover processes in the physical system. For example, the slowly evolving and moving low pressure systems in the atmosphere might impart persistence to daily rainfall. Or the slow drainage of groundwater reserves might impart correlation to successive annual flows of a river. Or stored photosynthates might impart correlation to successive annual values of tree-ring indices. Autocorrelation complicates the application of statistical tests by reducing the effective sample size. Autocorrelation can also complicate the identification of significant covariance or correlation between time series (e.g., precipitation with a tree-ring series). Autocorrelation implies that a time series is predictable, probabilistically, as future values are correlated with current and past values. Three tools for assessing the autocorrelation of a time series are (1) the time series plot, (2) the lagged scatterplot, and (3) the autocorrelation function. 3.1 Time series plot Positively autocorrelated series are sometimes referred to as persistent because positive departures from the mean tend to be followed by positive depatures from the mean, and negative departures from the mean tend to be followed by negative departures (Figure 3.1).
    [Show full text]
  • Stationary Processes
    Stationary processes Alejandro Ribeiro Dept. of Electrical and Systems Engineering University of Pennsylvania [email protected] http://www.seas.upenn.edu/users/~aribeiro/ November 25, 2019 Stoch. Systems Analysis Stationary processes 1 Stationary stochastic processes Stationary stochastic processes Autocorrelation function and wide sense stationary processes Fourier transforms Linear time invariant systems Power spectral density and linear filtering of stochastic processes Stoch. Systems Analysis Stationary processes 2 Stationary stochastic processes I All probabilities are invariant to time shits, i.e., for any s P[X (t1 + s) ≥ x1; X (t2 + s) ≥ x2;:::; X (tK + s) ≥ xK ] = P[X (t1) ≥ x1; X (t2) ≥ x2;:::; X (tK ) ≥ xK ] I If above relation is true process is called strictly stationary (SS) I First order stationary ) probs. of single variables are shift invariant P[X (t + s) ≥ x] = P [X (t) ≥ x] I Second order stationary ) joint probs. of pairs are shift invariant P[X (t1 + s) ≥ x1; X (t2 + s) ≥ x2] = P [X (t1) ≥ x1; X (t2) ≥ x2] Stoch. Systems Analysis Stationary processes 3 Pdfs and moments of stationary process I For SS process joint cdfs are shift invariant. Whereby, pdfs also are fX (t+s)(x) = fX (t)(x) = fX (0)(x) := fX (x) I As a consequence, the mean of a SS process is constant Z 1 Z 1 µ(t) := E [X (t)] = xfX (t)(x) = xfX (x) = µ −∞ −∞ I The variance of a SS process is also constant Z 1 Z 1 2 2 2 var [X (t)] := (x − µ) fX (t)(x) = (x − µ) fX (x) = σ −∞ −∞ I The power of a SS process (second moment) is also constant Z 1 Z 1 2 2 2 2 2 E X (t) := x fX (t)(x) = x fX (x) = σ + µ −∞ −∞ Stoch.
    [Show full text]
  • Solutions to Exercises in Stationary Stochastic Processes for Scientists and Engineers by Lindgren, Rootzén and Sandsten Chapman & Hall/CRC, 2013
    Solutions to exercises in Stationary stochastic processes for scientists and engineers by Lindgren, Rootzén and Sandsten Chapman & Hall/CRC, 2013 Georg Lindgren, Johan Sandberg, Maria Sandsten 2017 CENTRUM SCIENTIARUM MATHEMATICARUM Faculty of Engineering Centre for Mathematical Sciences Mathematical Statistics 1 Solutions to exercises in Stationary stochastic processes for scientists and engineers Mathematical Statistics Centre for Mathematical Sciences Lund University Box 118 SE-221 00 Lund, Sweden http://www.maths.lu.se c Georg Lindgren, Johan Sandberg, Maria Sandsten, 2017 Contents Preface v 2 Stationary processes 1 3 The Poisson process and its relatives 5 4 Spectral representations 9 5 Gaussian processes 13 6 Linear filters – general theory 17 7 AR, MA, and ARMA-models 21 8 Linear filters – applications 25 9 Frequency analysis and spectral estimation 29 iii iv CONTENTS Preface This booklet contains hints and solutions to exercises in Stationary stochastic processes for scientists and engineers by Georg Lindgren, Holger Rootzén, and Maria Sandsten, Chapman & Hall/CRC, 2013. The solutions have been adapted from course material used at Lund University on first courses in stationary processes for students in engineering programs as well as in mathematics, statistics, and science programs. The web page for the course during the fall semester 2013 gives an example of a schedule for a seven week period: http://www.maths.lu.se/matstat/kurser/fms045mas210/ Note that the chapter references in the material from the Lund University course do not exactly agree with those in the printed volume. v vi CONTENTS Chapter 2 Stationary processes 2:1. (a) 1, (b) a + b, (c) 13, (d) a2 + b2, (e) a2 + b2, (f) 1.
    [Show full text]
  • Statistical Tool for Soil Biology : 11. Autocorrelogram and Mantel Test
    ‘i Pl w f ’* Em J. 1996, (4), i Soil BioZ., 32 195-203 Statistical tool for soil biology. XI. Autocorrelogram and Mantel test Jean-Pierre Rossi Laboratoire d Ecologie des Sols Trofiicaux, ORSTOM/Université Paris 6, 32, uv. Varagnat, 93143 Bondy Cedex, France. E-mail: rossij@[email protected]. fr. Received October 23, 1996; accepted March 24, 1997. Abstract Autocorrelation analysis by Moran’s I and the Geary’s c coefficients is described and illustrated by the analysis of the spatial pattern of the tropical earthworm Clzuniodrilus ziehe (Eudrilidae). Simple and partial Mantel tests are presented and illustrated through the analysis various data sets. The interest of these methods for soil ecology is discussed. Keywords: Autocorrelation, correlogram, Mantel test, geostatistics, spatial distribution, earthworm, plant-parasitic nematode. L’outil statistique en biologie du sol. X.?. Autocorrélogramme et test de Mantel. Résumé L’analyse de l’autocorrélation par les indices I de Moran et c de Geary est décrite et illustrée à travers l’analyse de la distribution spatiale du ver de terre tropical Chuniodi-ibs zielae (Eudrilidae). Les tests simple et partiel de Mantel sont présentés et illustrés à travers l’analyse de jeux de données divers. L’intérêt de ces méthodes en écologie du sol est discuté. Mots-clés : Autocorrélation, corrélogramme, test de Mantel, géostatistiques, distribution spatiale, vers de terre, nématodes phytoparasites. INTRODUCTION the variance that appear to be related by a simple power law. The obvious interest of that method is Spatial heterogeneity is an inherent feature of that samples from various sites can be included in soil faunal communities with significant functional the analysis.
    [Show full text]
  • Applied Time Series Analysis
    Applied Time Series Analysis SS 2018 February 12, 2018 Dr. Marcel Dettling Institute for Data Analysis and Process Design Zurich University of Applied Sciences CH-8401 Winterthur Table of Contents 1 INTRODUCTION 1 1.1 PURPOSE 1 1.2 EXAMPLES 2 1.3 GOALS IN TIME SERIES ANALYSIS 8 2 MATHEMATICAL CONCEPTS 11 2.1 DEFINITION OF A TIME SERIES 11 2.2 STATIONARITY 11 2.3 TESTING STATIONARITY 13 3 TIME SERIES IN R 15 3.1 TIME SERIES CLASSES 15 3.2 DATES AND TIMES IN R 17 3.3 DATA IMPORT 21 4 DESCRIPTIVE ANALYSIS 23 4.1 VISUALIZATION 23 4.2 TRANSFORMATIONS 26 4.3 DECOMPOSITION 29 4.4 AUTOCORRELATION 50 4.5 PARTIAL AUTOCORRELATION 66 5 STATIONARY TIME SERIES MODELS 69 5.1 WHITE NOISE 69 5.2 ESTIMATING THE CONDITIONAL MEAN 70 5.3 AUTOREGRESSIVE MODELS 71 5.4 MOVING AVERAGE MODELS 85 5.5 ARMA(P,Q) MODELS 93 6 SARIMA AND GARCH MODELS 99 6.1 ARIMA MODELS 99 6.2 SARIMA MODELS 105 6.3 ARCH/GARCH MODELS 109 7 TIME SERIES REGRESSION 113 7.1 WHAT IS THE PROBLEM? 113 7.2 FINDING CORRELATED ERRORS 117 7.3 COCHRANE‐ORCUTT METHOD 124 7.4 GENERALIZED LEAST SQUARES 125 7.5 MISSING PREDICTOR VARIABLES 131 8 FORECASTING 137 8.1 STATIONARY TIME SERIES 138 8.2 SERIES WITH TREND AND SEASON 145 8.3 EXPONENTIAL SMOOTHING 152 9 MULTIVARIATE TIME SERIES ANALYSIS 161 9.1 PRACTICAL EXAMPLE 161 9.2 CROSS CORRELATION 165 9.3 PREWHITENING 168 9.4 TRANSFER FUNCTION MODELS 170 10 SPECTRAL ANALYSIS 175 10.1 DECOMPOSING IN THE FREQUENCY DOMAIN 175 10.2 THE SPECTRUM 179 10.3 REAL WORLD EXAMPLE 186 11 STATE SPACE MODELS 187 11.1 STATE SPACE FORMULATION 187 11.2 AR PROCESSES WITH MEASUREMENT NOISE 188 11.3 DYNAMIC LINEAR MODELS 191 ATSA 1 Introduction 1 Introduction 1.1 Purpose Time series data, i.e.
    [Show full text]
  • Quantitative Risk Management in R
    QUANTITATIVE RISK MANAGEMENT IN R Characteristics of volatile return series Quantitative Risk Management in R Log-returns compared with iid data ● Can financial returns be modeled as independent and identically distributed (iid)? ● Random walk model for log asset prices ● Implies that future price behavior cannot be predicted ● Instructive to compare real returns with iid data ● Real returns o!en show volatility clustering QUANTITATIVE RISK MANAGEMENT IN R Let’s practice! QUANTITATIVE RISK MANAGEMENT IN R Estimating serial correlation Quantitative Risk Management in R Sample autocorrelations ● Sample autocorrelation function (acf) measures correlation between variables separated by lag (k) ● Stationarity is implicitly assumed: ● Expected return constant over time ● Variance of return distribution always the same ● Correlation between returns k apart always the same ● Notation for sample autocorrelation: ⇢ˆ(k) Quantitative Risk Management in R The sample acf plot or correlogram > acf(ftse) Quantitative Risk Management in R The sample acf plot or correlogram > acf(abs(ftse)) QUANTITATIVE RISK MANAGEMENT IN R Let’s practice! QUANTITATIVE RISK MANAGEMENT IN R The Ljung-Box test Quantitative Risk Management in R Testing the iid hypothesis with the Ljung-Box test ● Numerical test calculated from squared sample autocorrelations up to certain lag ● Compared with chi-squared distribution with k degrees of freedom (df) ● Should also be carried out on absolute returns k ⇢ˆ(j)2 X2 = n(n + 2) n j j=1 X − Quantitative Risk Management in R Example of
    [Show full text]
  • Random Processes
    Chapter 6 Random Processes Random Process • A random process is a time-varying function that assigns the outcome of a random experiment to each time instant: X(t). • For a fixed (sample path): a random process is a time varying function, e.g., a signal. – For fixed t: a random process is a random variable. • If one scans all possible outcomes of the underlying random experiment, we shall get an ensemble of signals. • Random Process can be continuous or discrete • Real random process also called stochastic process – Example: Noise source (Noise can often be modeled as a Gaussian random process. An Ensemble of Signals Remember: RV maps Events à Constants RP maps Events à f(t) RP: Discrete and Continuous The set of all possible sample functions {v(t, E i)} is called the ensemble and defines the random process v(t) that describes the noise source. Sample functions of a binary random process. RP Characterization • Random variables x 1 , x 2 , . , x n represent amplitudes of sample functions at t 5 t 1 , t 2 , . , t n . – A random process can, therefore, be viewed as a collection of an infinite number of random variables: RP Characterization – First Order • CDF • PDF • Mean • Mean-Square Statistics of a Random Process RP Characterization – Second Order • The first order does not provide sufficient information as to how rapidly the RP is changing as a function of timeà We use second order estimation RP Characterization – Second Order • The first order does not provide sufficient information as to how rapidly the RP is changing as a function
    [Show full text]