DOCSLIB.ORG

Modelling and Control of Combustion Phasing of an Rcci Engine

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Modelling and Control of Combustion Phasing of an Rcci Engine Michigan Technological University Digital Commons @ Michigan Tech Dissertations, Master's Theses and Master's Dissertations, Master's Theses and Master's Reports - Open Reports 2015 MODELLING AND CONTROL OF COMBUSTION PHASING OF AN RCCI ENGINE Kaveh Khodadadi Sadabadi Michigan Technological University Follow this and additional works at: https://digitalcommons.mtu.edu/etds Part of the Mechanical Engineering Commons Copyright 2015 Kaveh Khodadadi Sadabadi Recommended Citation Khodadadi Sadabadi, Kaveh, "MODELLING AND CONTROL OF COMBUSTION PHASING OF AN RCCI ENGINE", Master's Thesis, Michigan Technological University, 2015. https://doi.org/10.37099/mtu.dc.etds/966 Follow this and additional works at: https://digitalcommons.mtu.edu/etds Part of the Mechanical Engineering Commons MODELLING AND CONTROL OF COMBUSTION PHASING OF AN RCCI ENGINE By Kaveh Khodadadi Sadabadi A THESIS Submitted in partial fulfillment of the requirements for the degree of MASTER OF SCIENCE In Mechanical Engineering MICHIGAN TECHNOLOGICAL UNIVERSITY 2015 © 2015 Kaveh Khodadadi Sadabadi This thesis has been approved in partial fulfillment of the requirements for the Degree of MASTER OF SCIENCE in Mechanical Engineering. Department of Mechanical Engineering-Engineering Mechanics Thesis Advisor: Dr. Mahdi Shahbakhti Committee Member: Dr. Jeffery Naber Committee Member: Dr. Jeffery Burl Department Chair: Dr. William W. Predebon ii Contents List of Figures ................................................................................................................................... v List of Definitions/Abbreviations ..................................................................................................... viii List of Symbols ................................................................................................................................ xi List of Subscripts ............................................................................................................................ xiii Preface ........................................................................................................................................... xiv Acknowledgment ............................................................................................................................ xv Abstract .......................................................................................................................................... xvi Chapter 1 ......................................................................................................................................... 1 1.1 Motivation for Reactivity Controlled Combustion Strategy ............................................... 3 1.2 Charge stratification and RCCI combustion strategy ....................................................... 5 1.3 RCCI Combustion Strategy-Challenges ........................................................................ 13 1.4 Research Scope and Thesis Organization .................................................................... 14 Chapter 2 ....................................................................................................................................... 17 2.1 Introduction to COM development ................................................................................. 18 2.2 Modelling RCCI combustion........................................................................................... 24 2.2.1 SOC estimation model ............................................................................................... 26 2.2.2 Control oriented modelling of combustion duration.................................................... 34 2.2.1 CA50 estimation model .............................................................................................. 39 2.3 RCCI Engine Data .......................................................................................................... 40 2.4 Results and Discussion .................................................................................................. 44 2.4.1 Polytropic compression constant ............................................................................... 44 2.4.2 Parameterizing MKIM ................................................................................................. 45 2.4.3 BD Estimation............................................................................................................. 49 2.4.1 Estimation of CA50 .................................................................................................... 51 Chapter 3 ....................................................................................................................................... 55 3.1 RCCI Dynamic Model ..................................................................................................... 56 iii 3.1.1 Intake Stroke .............................................................................................................. 56 3.1.2 Compression Stroke ................................................................................................... 60 3.1.3 Combustion ................................................................................................................ 60 3.1.4 Expansion Stroke ....................................................................................................... 61 3.1.5 Exhaust Blow-down .................................................................................................... 61 3.1.6 Physical Model Lay-out .............................................................................................. 62 3.2 Controller Design ........................................................................................................... 64 3.2.1 Simplified COM .......................................................................................................... 64 3.2.2 Model Linearization and Linear Quadratic Integral (LQI) Design ............................... 68 3.2.3 State estimator performance ...................................................................................... 71 3.2.4 CA50 Tracking Results .............................................................................................. 73 3.2.5 Disturbance Rejection ................................................................................................ 74 Chapter 4 ....................................................................................................................................... 76 4.2 Summary and Conclusion .............................................................................................. 76 4.3 Suggestions for Future Work ......................................................................................... 78 References ..................................................................................................................................... 80 ..................................................................................................................................... 86 ..................................................................................................................................... 96 ..................................................................................................................................... 97 ..................................................................................................................................... 98 ................................................................................................................................... 100 iv List of Figures Figure 1-1. EPA green house gas (GHG) and fuel economy regulations. The data in reference [1] was used to produce this figure. ...................................................................................................... 2 Figure 1-2. ߮ versus temperature for CD and RCCI combustion at 5° aTDC [4] .......................... 10 Figure 1-3. Thesis structure. .......................................................................................................... 16 Figure 2-1. Control-oriented auto-ignition models for compression ignition combustion concepts 20 Figure 2-2. Charge preparation in RCCI combustion technology .................................................. 26 Figure 2-3. RCCI combustion phenomenological model (Formation of auto-ignition pockets and staged ignition). .............................................................................................................................. 26 Figure 2-4. Graphical integration of 1ݓ߬ from IVC to SOC ............................................................ 28 Figure 2-5. KIVA simulation and experimental results for 1 bar BMEP experiment. The data to generate this figure is taken from [10-11]. ..................................................................................... 42 Figure 2-6. KIVA simulation and experimental results for 2.6 bar BMEP experiment. The data to generate this figure is taken from [10-11]. ..................................................................................... 42 Figure 2-7. Estimated SOC pressures vs. SOC pressures from KIVA simulations using the best numerical fit of ݇ܿ=1.35. ݁ܽݒ݁, ߪܽݒ݁, ݁݉ܽݔ indicate average error, standard deviation of error and maximum error, respectively. ......................................................................................................... 44 Figure 2-8. MKIM SOC prediction and KIVA simulation Data........................................................ 46 Figure
Load more

Recommended publications
  • T I S ^ E ' Cottons CUSTOMIZED KITCHENS 0^
    : : ' I '■ ;:'vV WEDKBBDAY, FEBRUARY 2,.lO li' JL ffba Wahtlkir tfnnrlrrBtpr Eurntog frrtJh Avenga Dnflr KsC Prsss Ron I at P. a WsaBSa rue tha fairth •« ill- •■t. iWk t \ ^ 9 , 6 8 0 lawet by aaow aarty FtMay; e of «ka AniH FYMay, mow amy ebaago «a i lul Town / I V. ManehtSner— A tity of Vittage Charm midbi t I m k Pwxda’t Vuflon nMOtben t» iDMt tUa ave* MANCHESTER, CONN„ THURSDAY, FEBRUARY 3,1949 PRKJE FOUR CENTS StatTjO at the 8^^" VOL. LX \T n„ NO. 105 (TWENTY PAGES) AtMy cltaC^l. where they wli) SMART YOUNO H O ifB M leave for a lobogfan party. 'I ( . ■ ■ The 0* Troop 16, Olrl President Congratulates Retiring Generals floouta, wm ba omitted thto week. ENTIRTAIN IN Sharp Partisan Rows The next meeting held World Gets Notice . Thuraday, Fhbniary 10, under the l c a ! 3 e ^ 0* Mia. Lealle Hoyt and SaT^tawrence MacQUpln, In T IA P A R T Y St. Jamaa’a adUwl hall. RedMove Will Not •In Senate and House An Important btialneae meeting a t the CoamopoHtan Club will b e , held Friday attemoon at two Be Let Hurt Unity o'clock In the Federation room of j center church houae, when the | mambera will vote on the revtaed i On Budget, Housing by-lawa. A talk on the “Ro- Real ^Significance Seen ^nen of Silver” wlU foUow the, Norway’s Own — Imalneaa aenlon, and a large at­ In Acheson’s Rejec­ tendance of merabera le hoped for. tion of Stalin’s' Lat­ Democratic Floor Lead­ Mra.
    [Show full text]
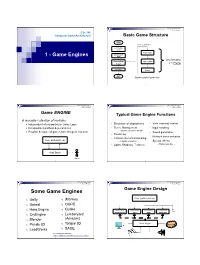
  • 165 Lecture Notes 1 - Game Engines Csc 165 Computer Game Architecture Basic Game Structure
    CSc 165 Lecture Notes 1 - Game Engines CSc 165 Computer Game Architecture Basic Game Structure Start while (!gameOver) Initialize system Player Input Initialize 1 - Game Engines game One iteration Game Main Logic Update Loop = 1 Frame Shutdown Render Exit “Tightly-coupled” game loop 2 CSc 165 Lecture Notes CSc 165 Lecture Notes 1 - Game Engines 1 - Game Engines Game ENGINE Typical Game Engine Functions A reusable collection of modules . Independent of any particular Game Logic • Simulation of elapsed time • View (camera) control . Encapsulates platform dependencies • Scene Management • Input handling o Objects, geometry details . Possible because all games have things in common • Sound generation • Rendering • Network communication • Collision Detection/Handling Game Application Logic o Physics simulation • Special effects • Lights, Shadows, Textures o Explosions, fire, … Game Engine Player 3 4 CSc 165 Lecture Notes CSc 165 Lecture Notes 1 - Game Engines 1 - Game Engines Game Engine Design Some Game Engines Game Application Logic o Unity o jMonkey o Unreal o OGRE o Hero Engine o Quake <<interface>> <<interface>> <<interface>> <<interface>> … other RenderSystem Input Audio Networking o CryEngine o Lumberyard o Blender (Amazon) o Game Engine o Panda 3D Torque 3D Network o LeadWerks o SAGE For an expanded list see: http://en.wikipedia.org/wiki/List_of_game_engines 5 6 CSc 165 Lecture Notes CSc 165 Lecture Notes 1 - Game Engines 1 - Game Engines RAGE : “Raymond’s Awesome Game Engine” Abstracting Game Structure A collection of Java packages
    [Show full text]
  • 14 CFR Part 25
    Pt. 25 14 CFR Ch. I (1–1–13 Edition) TABLE I.—HIRF ENVIRONMENT I (5) From 400 MHz to 8 gigahertz (GHz), use radiated susceptibility tests at a minimum Field strength of 150 V/m peak with pulse modulation of 4 Frequency (volts/meter) percent duty cycle with a 1 kHz pulse repeti- Peak Average tion frequency. This signal must be switched on and off at a rate of 1 Hz with a duty cycle 10 kHz–2 MHz ................................... 50 50 of 50 percent. 2 MHz–30 MHz ................................. 100 100 (d) Equipment HIRF Test Level 2. Equipment 30 MHz–100 MHz ............................. 50 50 HIRF test level 2 is HIRF environment II in 100 MHz–400 MHz ........................... 100 100 table II of this appendix reduced by accept- 400 MHz–700 MHz ........................... 700 50 able aircraft transfer function and attenu- 700 MHz–1 GHz ................................ 700 100 ation curves. Testing must cover the fre- GHz–2 GHz ....................................... 2,000 200 2 GHz–6 GHz .................................... 3,000 200 quency band of 10 kHz to 8 GHz. 6 GHz–8 GHz .................................... 1,000 200 (e) Equipment HIRF Test Level 3. (1) From 10 8 GHz–12 GHz .................................. 3,000 300 kHz to 400 MHz, use conducted susceptibility 12 GHz–18 GHz ................................ 2,000 200 tests, starting at a minimum of 0.15 mA at 10 18 GHz–40 GHz ................................ 600 200 kHz, increasing 20 dB per frequency decade In this table, the higher field strength applies at the fre- to a minimum of 7.5 mA at 500 kHz. quency band edges. (2) From 500 kHz to 40 MHz, use conducted susceptibility tests at a minimum of 7.5 mA.
    [Show full text]
  • Spitzer SAGE-SMC Infrared Photometry of Massive Stars in the Small Magellanic Cloud Bonanos, A.Z.; Lennon, D.J.; Köhlinger, F.; Loon, J.T
    Spitzer SAGE-SMC Infrared Photometry of Massive Stars in the Small Magellanic Cloud Bonanos, A.Z.; Lennon, D.J.; Köhlinger, F.; Loon, J.T. van; Massa, D.L.; Sewilo, M.; ... ; Whitney, B.A. Citation Bonanos, A. Z., Lennon, D. J., Köhlinger, F., Loon, J. T. van, Massa, D. L., Sewilo, M., … Whitney, B. A. (2010). Spitzer SAGE-SMC Infrared Photometry of Massive Stars in the Small Magellanic Cloud. The Astronomical Journal, 140(2), 416-429. doi:10.1088/0004-6256/140/2/416 Version: Not Applicable (or Unknown) License: Leiden University Non-exclusive license Downloaded from: https://hdl.handle.net/1887/61635 Note: To cite this publication please use the final published version (if applicable). The Astronomical Journal, 140:416–429, 2010 August doi:10.1088/0004-6256/140/2/416 C 2010. The American Astronomical Society. All rights reserved. Printed in the U.S.A. SPITZER SAGE-SMC INFRARED PHOTOMETRY OF MASSIVE STARS IN THE SMALL MAGELLANIC CLOUD A. Z. Bonanos1,D.J.Lennon2,3,F.Kohlinger¨ 4, J. Th. van Loon5,D.L.Massa2,M.Sewilo2,C.J.Evans6, N. Panagia2,7,8, B. L. Babler9, M. Block10, S. Bracker9, C. W. Engelbracht9, K. D. Gordon2,J.L.Hora11, R. Indebetouw12, M. R. Meade9, M. Meixner2,K.A.Misselt10, T. P. Robitaille11,B.Shiao2, and B. A. Whitney13 1 Institute of Astronomy & Astrophysics, National Observatory of Athens, I. Metaxa & Vas. Pavlou St., P. Penteli, 15236 Athens, Greece; [email protected] 2 Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA; [email protected], [email protected], [email protected], [email protected], [email protected], [email protected], [email protected] 3 European Space Agency, Research and Scientific Support Department, Baltimore, MD 21218, USA 4 Department of Physics and Astronomy, Heidelberg University, Albert-Ueberle-Str.
    [Show full text]
  • Participatory Gaming Culture
    Master thesis Participatory gaming culture: Indie game design as dialogue between player & creator Martijn van Best student ID: 3175421 [email protected] New Media Studies Faculty of Humanities UTRECHT UNIVERSITY Course code: 200700088 THE-Scriptie / MA NMDC Supervisor: Erna Kotkamp Second reader: René Glas DATE: March 28th, 2011 1 To Mieke 2 Abstract In this thesis I argue that the current dichotomy between indie game design and mainstream design based on commercial appeal versus creative audacity is non-constructive. Instead, I wish to investigate to what extent indie game designers are able to establish a personal dialogue with their audience through their game. I frame independent game design as a participatory culture in which indies alter and modify existing game design conventions through a practice called abusive game design. This is a concept developed by Douglas Wilson and Miguel Sicart. Players who wish to master (partially) abusive games, need to learn about the designer's intentions rather than the game system. I argue that a designer's visibility in this way allows for a dialogue between creator and player. However, in a case study of indie title Super Crate Box (2010), it appears that in order to maintain a sense of fun, certain conventions of mainstream game design need to be adhered to. Indie designers, who often have the most visible and personal relationship with their audience, need to navigate between their wish for a personal connection with players and user friendly, but 'faceless' design. Scaling the tipping point too much to the abusive side instead of the conventional one, may be counter to designers' wishes to create an enjoyable game.
    [Show full text]
  • Engineering Design Using Game-Enhanced CAD: the Potential to Augment the User Experience with Game Elements
    Heriot-Watt University Research Gateway Engineering design using game-enhanced CAD: The potential to augment the user experience with game elements Citation for published version: Kosmadoudi, Z, Lim, T, Ritchie, JM, Louchart, S, Liu, Y & Sung, R 2012, 'Engineering design using game- enhanced CAD: The potential to augment the user experience with game elements', Computer-Aided Design, vol. 45, no. 3, pp. 777-795. https://doi.org/10.1016/j.cad.2012.08.001 Digital Object Identifier (DOI): 10.1016/j.cad.2012.08.001 Link: Link to publication record in Heriot-Watt Research Portal Document Version: Early version, also known as pre-print Published In: Computer-Aided Design General rights Copyright for the publications made accessible via Heriot-Watt Research Portal is retained by the author(s) and / or other copyright owners and it is a condition of accessing these publications that users recognise and abide by the legal requirements associated with these rights. Take down policy Heriot-Watt University has made every reasonable effort to ensure that the content in Heriot-Watt Research Portal complies with UK legislation. If you believe that the public display of this file breaches copyright please contact [email protected] providing details, and we will remove access to the work immediately and investigate your claim. Download date: 01. Oct. 2021 Accepted Manuscript Engineering design using game-enhanced CAD: The potential to augment the user experience with game elements Zoe Kosmadoudi, Theodore Lim, James Ritchie, Sandy Louchart, Ying Liu, Raymond Sung PII: S0010-4485(12)00169-8 DOI: 10.1016/j.cad.2012.08.001 Reference: JCAD 1963 To appear in: Computer-Aided Design Received date: 10 October 2011 Accepted date: 4 August 2012 Please cite this article as: Kosmadoudi Z, Lim T, Ritchie J, Louchart S, Liu Y, Sung R.
    [Show full text]
  • Proquest Dissertations
    INFORMATION TO USERS This manuscript has been reproduced from the microfilm master. UMI films the text directly from the original or copy submitted. Thus, some thesis and dissertation copies are in typewriter face, while others may be from any type of computer printer. The quality of this reproduction is dependent upon the quality of the copy submitted. Broken or indistinct print, colored or poor quality illustrations and photographs, print bleedthrough, substandard margins, and improper alignment can adversely affect reproduction. In the unlikely event that the author did not send UMI a complete manuscript and there are missing pages, these will be noted. Also, if unauthorized copyright material had to be removed, a note will indicate the deletion. Oversize materials (e.g., maps, drawings, charts) are reproduced by sectioning the original, beginning at the upper left-hand comer and continuing from left to right in equal sections with small overlaps. Each original is also photographed in one exposure and is included in reduced form at the back of the book. Photographs included in the original manuscript have been reproduced xerographically in this copy. Higher quality 6” x 9” black and white photographic prints are available for any photographs or illustrations appearing in this copy for an additional charge. Contact UMI directly to order. UMI Bell & Howell Information and Learning 300 North Zeeb Road, Ann Aibor, Ml 48106-1346 USA 800-521-0600 3D VIRTUAL WORLDS AND LEARNING: AN ANALYSIS OF THE IMPACT OF DESIGN AFFORDANCES AND LIMITATIONS IN ACTIVE WORLDS, BLAXXUN INTERACTIVE, AND ONLIVE! TRAVELER; AND A STUDY OF THE IMPLEMENTATION OF ACTIVE WORLDS FOR FORMAL AND INFORMAL EDUCATION DISSERTATION Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio State University By Michele D.
    [Show full text]
  • Guia De Desenvolvimento De Jogos Para Programadores Independentes
    Guia de desenvolvimento de jogos para programadores independentes LUÍS MIGUEL DIAS FERNANDES Outubro de 2015 Guia de desenvolvimento de jogos para programadores independentes Luís Miguel Dias Fernandes Dissertação para obtenção do Grau de Mestre em Engenharia Informática, Área de Especialização em Sistemas Gráficos e Multimédia Orientador: Filipe de Faria Pacheco, PhD Júri: Presidente: [Nome do Presidente, Categoria, Escola] Vogais: [Nome do Vogal1, Categoria, Escola] [Nome do Vogal2, Categoria, Escola] (até 4 vogais) Porto, Outubro 2015 ii Resumo Os vídeo jogos ou jogos de computador têm vindo a crescer na sua relação com o público ganhando terreno e credibilidade nos benefícios que os jogadores obtêm quando usam este tipo de software, indo esses benefícios para além do divertimento associado à palavra jogo no seu sentido etimológico. Nos últimos anos cada vez mais o mercado e algumas das mais reputadas instituições de ensino têm dedicado especial atenção a este tipo de software, englobando nesses estudos diversas áreas desde a engenharia à saúde, incluindo ainda, estudos de cariz psicológico e sociológico reveladores de que estas experiências de entretenimento, cada vez mais disponíveis a todos, têm influência na sua envolvente de integração e relação com outros fenómenos de cariz social. Apreciado o estado da arte esta tese tem como principal objetivo servir de guia de iniciação a individuais ou pequenas equipas da área de desenvolvimento de software no caminho para o desenvolvimento de jogos de vídeo independentes, apresentando uma análise cuidada capaz de apoiar as equipas desde o momento zero, estando o mesmo estruturado de forma a refletir o entendimento das bases teóricas em que o desenvolvimento deste tipo de software assenta, o estado da arte sobre plataformas, análise de mercado e indústria, metodologias de desenvolvimento e equipas, e ainda analisadas algumas das mais relevantes ferramentas de desenvolvimento e criação de conteúdos.
    [Show full text]
  • An Overview of the Steamie Educational Game Engine
    Session F3B An Overview of the STEAMiE Educational Game Engine Scott Nykl, Chad Mourning, Mitchell Leitch, David Chelberg, Teresa Franklin, and Chang Liu Ohio University, [email protected], [email protected], [email protected], [email protected], [email protected], [email protected] Abstract - Today, there exists a significant disparity in tools to create educational games and the tools’ the degree of technological development between shortcomings are described below. commercial and educational games. The STEAMiE Educational Engine is a cutting-edge system used to I. Recreational Engines create advanced, realistic, immersive learning environments. These environments have been shown to The Torque Game Engine is one of the leading independent influence comprehension and retention of hard-to-teach developer game engines [1]. There are multiple ways in science concepts. This paper will present an overview of which SEE is superior. First, Torque supports basic physics: the features of our STEAMiE Educational Engine and things can fall, go in a straight line, follow a parabola, and how to use it to create games/simulations capable of collide with other objects [1]. In SEE the physics engine enhancing a user’s learning experience. provides much higher fidelity; SEE can maintain realistic multi-object interactions that cascade indefinitely. Second, The STEAMiE Educational Engine contains a rich Torque, similar to many existing engines, utilizes its own feature set allowing for development of powerful “C++ like” scripting language. Scripting languages allow modules within a short period of time. From a certain common scenarios to be easily implemented; development point of view, the STEAMiE Educational however, as the complexity of a scenario increases the Engine’s object oriented design is modular and can be limitations of the scripting language force the developer to easily extended to support new functionality in a timely “jump through hoops” to achieve their goal.
    [Show full text]
  • SMOKE MANAGEMENT GUIDE for PRESCRIBED and WILDLAND FIRE 2001 Edition
    SMOKE MANAGEMENT GUIDE FOR PRESCRIBED AND WILDLAND FIRE 2001 Edition EDITORS/COMPILERS: PRODUCED BY: Colin C. Hardy National Wildfire Coordinating Group Roger D. Ottmar Fire Use Working Team Janice L. Peterson John E. Core Paula Seamon Additional copies of this publication may be ordered by mail/fax from: National Interagency Fire Center, ATTN: Great Basin Cache Supply Office 3833 S. Development Avenue Boise, Idaho 83705. Fax: 208-387-5573. Order NFES 1279 An electronic copy of this document is available at http://www.nwcg.gov. ________________________________________________________________________ The National Wildfire Coordinating Group (NWCG) has developed this information for the guidance of its member agencies and is not responsible for the interpretation or use of this information by anyone except the member agencies. The use of trade, firm, or corporation names in this publication is for the information and convenience of the reader and does not constitute an endorse- ment by NWCG of any product or service to the exclusion of others that may be suitable. 2001 Smoke Management Guide Forward Forward The National Wildfire Coordinating Group’s (NWCG) Fire Use Working Team1 has assumed overall responsibility for sponsoring the development and production of this revised Smoke Management Guide for Prescribed and Wildland Fire (the “Guide”). The Mission Statement for the Fire Use Work- ing Team includes the need to coordinate and advocate the use of fire to achieve management objec- tives, and to promote a greater understanding of the role of fire and its effects. The Fire Use Working Team recognizes that the ignition of wildland fuels by land managers, or the use of wildland fires ignited by natural causes to achieve specific management objectives is receiving continued emphasis from fire management specialists, land managers, environmental groups, politicians and the general public.
    [Show full text]
  • Challenges for Game Designers Brenda Brathwaite And
    CHALLENGES FOR GAME DESIGNERS BRENDA BRATHWAITE AND IAN SCHREIBER Charles River Media A part of Course Technology, Cengage Learning Australia, Brazil, Japan, Korea, Mexico, Singapore, Spain, United Kingdom, United States Challenges for Game Designers © 2009 Course Technology, a part of Cengage Learning. ALL RIGHTS RESERVED. No part of this work covered by the copyright Brenda Brathwaite and Ian Schreiber herein may be reproduced, transmitted, stored, or used in any form or by any means graphic, electronic, or mechanical, including but not limited to photocopying, recording, scanning, digitizing, taping, Web distribution, Publisher and General Manager, information networks, or information storage and retrieval systems, except Course Technology PTR: as permitted under Section 107 or 108 of the 1976 United States Copyright Stacy L. Hiquet Act, without the prior written permission of the publisher. Associate Director of Marketing: For product information and technology assistance, contact us at Sarah Panella Cengage Learning Customer & Sales Support, 1-800-354-9706 For permission to use material from this text or product, Content Project Manager: submit all requests online at cengage.com/permissions Jessica McNavich Further permissions questions can be emailed to [email protected] Marketing Manager: Jordan Casey All trademarks are the property of their respective owners. Acquisitions Editor: Heather Hurley Library of Congress Control Number: 2008929225 Project and Copy Editor: Marta Justak ISBN-13: 978-1-58450-580-8 ISBN-10: 1-58450-580-X CRM Editorial Services Coordinator: Jen Blaney eISBN-10: 1-58450-623-7 Course Technology Interior Layout: Jill Flores 25 Thomson Place Boston, MA 02210 USA Cover Designer: Tyler Creative Services Cengage Learning is a leading provider of customized learning solutions with office locations around the globe, including Singapore, the United Kingdom, Indexer: Sharon Hilgenberg Australia, Mexico, Brazil, and Japan.
    [Show full text]
  • MANUAL Riding Star Manual 1
    MANUAL Riding Star Manual 1. SYSTEM REQUIREMENTS TABLE of CONTENTS Minimum system requirements: Windows 2000/XP, Intel Pentium (or similar AMD) 1.5 GHz, 256 MB 1. SYSTEM REQUIREMENTS 3 6. THE DISCIPLINES 11 RAM, DirectX® 9, Direct 3D compatible graphics card with 64MB RAM, 2. INSTALLATION AND STARTING DRESSAGE 11 DirectSound compatible sound card, mouse, keyboard, 8x CD-ROM. THE GAME 3 Displays 12 3. CONTROLS 4 Preview of the fi gures 12 Recommended system requirements: 4. MAIN MENU 5 Dressage indicator 12 Windows 2000/XP, Intel Pentium (or similar AMD) 1.5 GHz, 512 MB QUICK GAME 5 Collections 13 RAM, DirectX® 9, Direct 3D compatible graphics card with 128 MB CAREER 5 Special fi gures 13 RAM, DirectSound compatible sound card, mouse, keyboard, 8x CD- OPTIONS 5 Example 14 ROM. Performance on notebook models may vary. QUIT 5 SHOW JUMPING 15 5. YOUR CAREER 5 Displays 16 PLAYER PROFILE 6 Rules 17 2. INSTALLATION AND STARTING THE GAME GAME CHARACTER 6 CROSS COUNTRY 18 THE COURTYARD 6 7. CREDITS 20 Open the CD-ROM drive of your computer and place the Riding Star THE OFFICE 7 CD in the drive. The game will then start automatically. If Riding Star YOUR FIRST HORSE 7 does not run automatically, double-click on the “RidingStar3.exe” fi le in TUTORIAL 7 the CD folder, found in “My Computer”, and then follow the on-screen THE CARE AREA 8 instructions to install Riding Star. Performance parameters 8 Care parameters 8 DirectX 9 or higher should be installed to play Riding Star properly.
    [Show full text]