The Dynamics of Legged Locomotion: Models, Analyses, and Challenges
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Compression Garments for Leg Lymphoedema
Compression garments for leg lymphoedema You have been fitted with a compression garment to help reduce the lymphoedema in your leg. Compression stockings work by limiting the amount of fluid building up in your leg. They provide firm support, enabling the muscles to pump fluid away more effectively. They provide most pressure at the foot and less at the top of the leg so fluid is pushed out of the limb where it will drain away more easily. How do I wear it? • Wear your garment every day to control the swelling in your leg. • Put your garment on as soon as possible after getting up in the morning. This is because as soon as you stand up and start to move around extra fluid goes into your leg and it begins to swell. • Take the garment off before bedtime unless otherwise instructed by your therapist. We appreciate that in hot weather garments can be uncomfortable, but unfortunately this is when it is important to wear it as the heat can increase the swelling. If you would like to leave off your garment for a special occasion please ask the clinic for advice. What should I look out for? Your garment should feel firm but not uncomfortable: • If you notice the garment is rubbing or cutting in, adjust the garment or remove it and reapply it. • If your garment feels tight during the day, try and think about what may have caused this. If you have been busy, sit down and elevate your leg and rest for at least 30 minutes. -

Sports Ankle Injuries Assessment and Management
FOCUS Sports injuries Sports ankle injuries Drew Slimmon Peter Brukner Assessment and management Background Case study Lucia is a female, 16 years of age, who plays netball with the Sports ankle injuries present commonly in the general state under 17s netball team. She presents with an ankle injury practice setting. The majority of these injuries are inversion sustained at training the previous night. She is on crutches and plantar flexion injuries that result in damage to the and is nonweight bearing. Examination raises the possibility of lateral ligament complex. a fracture, but X-ray is negative. You diagnose a severe lateral Objective ligament sprain and manage Lucia with ice, a compression The aim of this article is to review the assessment and bandage and a backslab initially. She then progresses through management of sports ankle injuries in the general practice a 6 week rehabilitation program and you recommend she wear setting. an ankle brace for at least 6 months. Discussion Assessment of an ankle injury begins with a detailed history to determine the severity, mechanism and velocity of the injury, what happened immediately after and whether there is a past history of inadequately rehabilitated ankle injury. Examination involves assessment of weight bearing, inspection, palpation, movement, and application of special examination tests. Plain X-rays may be helpful to exclude a fracture. If the diagnosis is uncertain, consider second The majority of ankle injuries are inversion and plantar line investigations including bone scan, computerised flexion injuries that result in damage to the lateral tomography or magnetic resonance imaging, and referral to a ligament complex (Figure 1). -
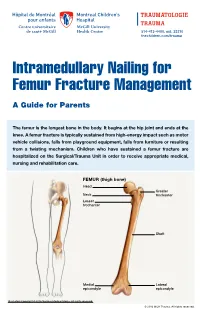
Intramedullary Nailing for Femur Fracture Management a Guide for Parents
514-412-4400, ext. 23310 thechildren.com/trauma Intramedullary Nailing for Femur Fracture Management A Guide for Parents The femur is the longest bone in the body. It begins at the hip joint and ends at the knee. A femur fracture is typically sustained from high-energy impact such as motor vehicle collisions, falls from playground equipment, falls from furniture or resulting from a twisting mechanism. Children who have sustained a femur fracture are hospitalized on the Surgical/Trauma Unit in order to receive appropriate medical, nursing and rehabilitation care. FEMUR (thigh bone) Head Greater Neck trochanter Lesser trochanter Shaft Medial Lateral epicondyle epicondyle Illustration Copyright © 2016 Nucleus Medical Media, All rights reserved. © 2016 MCH Trauma. All rights reserved. FEMUR FRACTURE MANAGEMENT The pediatric Orthopedic Surgeon will assess your child in order to determine the optimal treatment method. Treatment goals include: achieving proper bone realignment, rapid healing, and the return to normal daily activities. The treatment method chosen is primarily based on the child’s age but also taken into consideration are: fracture type, location and other injuries sustained if applicable. Prior to the surgery, your child may be placed in skin traction. This will ensure the bone is in an optimal healing position until it is surgically repaired. Occasionally, traction may be used for a longer period of time. The surgeon will determine if this management is needed based on the specific fracture type and/or location. ELASTIC/FLEXIBLE INTRAMEDULLARY NAILING This surgery is performed by the Orthopedic Surgeon in the Operating Room under general anesthesia. The surgeon will usually make two small incisions near the knee joint in order to insert two flexible titanium rods (intramedullary nails) Flexible through the femur. -

Volume 28 Contemporary Mathematics
Fluids and Plasmas: Geometry and Dynamics AMERICAII MATHEMATICAL SOCIETY VOLUME 28 http://dx.doi.org/10.1090/conm/028 CONTEMPORARY MATHEMATICS Titles in this Series Volume 1 Markov random fields and their applications, Ross Kindermann and J. Laurie Snell 2 Proceedings of the conference on integration, topology, and geometry in linear spaces, William H. Graves. Editor 3 The closed graph and P-closed graph properties in general topology, T. R. Hamlett and L. L. Herrington 4 Problems of elastic stability and vibrations, Vadim Komkov. Editor 5 Rational constructions of modules for simple Lie algebras, George B. Seligman 6 Umbral calculus and Hopf algebras, Robert Morris. Editor 7 Complex contour integral representation of cardinal spline functions, Walter Schempp 8 Ordered fields and real algebraic geometry, D. W. Dubois and T. Recio. Editors 9 Papers in algebra, analysis and statistics, R. Lidl. Editor 10 Operator algebras and K-theory, Ronald G. Douglas and Claude Schochet. Editors 11 Plane ellipticity and related problems, Robert P. Gilbert. Editor 12 Symposium on algebraic topology in honor of Jose Adem, Samuel Gitler. Editor 1l Algebraists' homage: Papers in ring theory and related topics, S. A. Amitsur. D. J. Saltman and G. B. Seligman. Editors 14 Lectures on Nielsen fixed point theory, Boju Jiang 15 Advanced analytic number theory. Part 1: Ramification theoretic methods, Carlos J. Moreno 16 Complex representations of GL(2, K) for finite fields K, llya Piatetski-Shapiro 17 Nonlinear partial differential equations, Joel A. Smoller. Editor 18 Fix~t' points and nonexpansive mappings, Robert C. Sine. Editor 19 Proceedings of the Northwestern homotopy theory conference, Haynes R. -

January 2013 Prizes and Awards
January 2013 Prizes and Awards 4:25 P.M., Thursday, January 10, 2013 PROGRAM SUMMARY OF AWARDS OPENING REMARKS FOR AMS Eric Friedlander, President LEVI L. CONANT PRIZE: JOHN BAEZ, JOHN HUERTA American Mathematical Society E. H. MOORE RESEARCH ARTICLE PRIZE: MICHAEL LARSEN, RICHARD PINK DEBORAH AND FRANKLIN TEPPER HAIMO AWARDS FOR DISTINGUISHED COLLEGE OR UNIVERSITY DAVID P. ROBBINS PRIZE: ALEXANDER RAZBOROV TEACHING OF MATHEMATICS RUTH LYTTLE SATTER PRIZE IN MATHEMATICS: MARYAM MIRZAKHANI Mathematical Association of America LEROY P. STEELE PRIZE FOR LIFETIME ACHIEVEMENT: YAKOV SINAI EULER BOOK PRIZE LEROY P. STEELE PRIZE FOR MATHEMATICAL EXPOSITION: JOHN GUCKENHEIMER, PHILIP HOLMES Mathematical Association of America LEROY P. STEELE PRIZE FOR SEMINAL CONTRIBUTION TO RESEARCH: SAHARON SHELAH LEVI L. CONANT PRIZE OSWALD VEBLEN PRIZE IN GEOMETRY: IAN AGOL, DANIEL WISE American Mathematical Society DAVID P. ROBBINS PRIZE FOR AMS-SIAM American Mathematical Society NORBERT WIENER PRIZE IN APPLIED MATHEMATICS: ANDREW J. MAJDA OSWALD VEBLEN PRIZE IN GEOMETRY FOR AMS-MAA-SIAM American Mathematical Society FRANK AND BRENNIE MORGAN PRIZE FOR OUTSTANDING RESEARCH IN MATHEMATICS BY ALICE T. SCHAFER PRIZE FOR EXCELLENCE IN MATHEMATICS BY AN UNDERGRADUATE WOMAN AN UNDERGRADUATE STUDENT: FAN WEI Association for Women in Mathematics FOR AWM LOUISE HAY AWARD FOR CONTRIBUTIONS TO MATHEMATICS EDUCATION LOUISE HAY AWARD FOR CONTRIBUTIONS TO MATHEMATICS EDUCATION: AMY COHEN Association for Women in Mathematics M. GWENETH HUMPHREYS AWARD FOR MENTORSHIP OF UNDERGRADUATE -

ANTERIOR KNEE PAIN Home Exercises
ANTERIOR KNEE PAIN Home Exercises Anterior knee pain is pain that occurs at the front and center of the knee. It can be caused by many different problems, including: • Weak or overused muscles • Chondromalacia of the patella (softening and breakdown of the cartilage on the underside of the kneecap) • Inflammations and tendon injury (bursitis, tendonitis) • Loose ligaments with instability of the kneecap • Articular cartilage damage (chondromalacia patella) • Swelling due to fluid buildup in the knee joint • An overload of the extensor mechanism of the knee with or without malalignment of the patella You may feel pain after exercising or when you sit too long. The pain may be a nagging ache or an occasional sharp twinge. Because the pain is around the front of your knee, treatment has traditionally focused on the knee itself and may include taping or bracing the kneecap, or patel- la, and/ or strengthening the thigh muscle—the quadriceps—that helps control your kneecap to improve the contact area between the kneecap and the thigh bone, or femur, beneath it. Howev- er, recent evidence suggests that strengthening your hip and core muscles can also help. The control of your knee from side to side comes from the glutes and core control; that is why those areas are so important in management of anterior knee pain. The exercises below will work on a combination of flexibility and strength of your knee, hip, and core. Although some soreness with exercise is expected, we do not want any sharp pain–pain that gets worse with each rep of an exercise or any increased soreness for more than 24 hours. -

How to Self-Bandage Your Leg(S) and Feet to Reduce Lymphedema (Swelling)
Form: D-8519 How to Self-Bandage Your Leg(s) and Feet to Reduce Lymphedema (Swelling) For patients with lower body lymphedema who have had treatment for cancer, including: • Removal of lymph nodes in the pelvis • Removal of lymph nodes in the groin, or • Radiation to the pelvis Read this resource to learn: • Who needs self-bandaging • Why self-bandaging is important • How to do self-bandaging Disclaimer: This pamphlet is for patients with lymphedema. It is a guide to help patients manage leg swelling with bandages. It is only to be used after the patient has been taught bandaging by a clinician at the Cancer Rehabilitation and Survivorship (CRS) Clinic at Princess Margaret Cancer Centre. Do not self-bandage if you have an infection in your abdomen, leg(s) or feet. Signs of an infection may include: • Swelling in these areas and redness of the skin (this redness can quickly spread) • Pain in your leg(s) or feet • Tenderness and/or warmth in your leg(s) or feet • Fever, chills or feeling unwell If you have an infection or think you have an infection, go to: • Your Family Doctor • Walk-in Clinic • Urgent Care Clinic If no Walk-in clinic is open, go to the closest hospital Emergency Department. 2 What is the lymphatic system? Your lymphatic system removes extra fluid and waste from your body. It plays an important role in how your immune system works. Your lymphatic system is made up of lymph nodes that are linked by lymph vessels. Your lymph nodes are bean-shaped organs that are found all over your body. -

Back of Leg I
Back of Leg I Dr. Garima Sehgal Associate Professor “Only those who risk going too far, can possibly find King George’s Medical University out how far one can go.” UP, Lucknow — T.S. Elliot DISCLAIMER Presentation has been made only for educational purpose Images and data used in the presentation have been taken from various textbooks and other online resources Author of the presentation claims no ownership for this material Learning Objectives By the end of this teaching session on Back of leg – I all the MBBS 1st year students must be able to: • Enumerate the contents of superficial fascia of back of leg • Write a short note on small saphenous vein • Describe cutaneous innervation in the back of leg • Write a short note on sural nerve • Enumerate the boundaries of posterior compartment of leg • Enumerate the fascial compartments in back of leg & their contents • Write a short note on flexor retinaculum of leg- its attachments & structures passing underneath • Describe the origin, insertion nerve supply and actions of superficial muscles of the posterior compartment of leg Introduction- Back of Leg / Calf • Powerful superficial antigravity muscles • (gastrocnemius, soleus) • Muscles are large in size • Inserted into the heel • Raise the heel during walking Superficial fascia of Back of leg • Contains superficial veins- • small saphenous vein with its tributaries • part of course of great saphenous vein • Cutaneous nerves in the back of leg- 1. Saphenous nerve 2. Posterior division of medial cutaneous nerve of thigh 3. Posterior cutaneous -

Getting a Leg up on Land
GETTING A LEG UP in the almost four billion years since life on earth oozed into existence, evolution has generated some marvelous metamorphoses. One of the most spectacular is surely that which produced terrestrial creatures ON bearing limbs, fingers and toes from water-bound fish with fins. Today this group, the tetrapods, encompasses everything from birds and their dinosaur ancestors to lizards, snakes, turtles, frogs and mammals, in- cluding us. Some of these animals have modified or lost their limbs, but their common ancestor had them—two in front and two in back, where LAND fins once flicked instead. Recent fossil discoveries cast The replacement of fins with limbs was a crucial step in this transfor- mation, but it was by no means the only one. As tetrapods ventured onto light on the evolution of shore, they encountered challenges that no vertebrate had ever faced be- four-limbed animals from fish fore—it was not just a matter of developing legs and walking away. Land is a radically different medium from water, and to conquer it, tetrapods BY JENNIFER A. CLACK had to evolve novel ways to breathe, hear, and contend with gravity—the list goes on. Once this extreme makeover reached completion, however, the land was theirs to exploit. Until about 15 years ago, paleontologists understood very little about the sequence of events that made up the transition from fish to tetrapod. We knew that tetrapods had evolved from fish with fleshy fins akin to today’s lungfish and coelacanth, a relation first proposed by American paleontologist Edward D. -

Alexander 2013 Principles-Of-Animal-Locomotion.Pdf
.................................................... Principles of Animal Locomotion Principles of Animal Locomotion ..................................................... R. McNeill Alexander PRINCETON UNIVERSITY PRESS PRINCETON AND OXFORD Copyright © 2003 by Princeton University Press Published by Princeton University Press, 41 William Street, Princeton, New Jersey 08540 In the United Kingdom: Princeton University Press, 3 Market Place, Woodstock, Oxfordshire OX20 1SY All Rights Reserved Second printing, and first paperback printing, 2006 Paperback ISBN-13: 978-0-691-12634-0 Paperback ISBN-10: 0-691-12634-8 The Library of Congress has cataloged the cloth edition of this book as follows Alexander, R. McNeill. Principles of animal locomotion / R. McNeill Alexander. p. cm. Includes bibliographical references (p. ). ISBN 0-691-08678-8 (alk. paper) 1. Animal locomotion. I. Title. QP301.A2963 2002 591.47′9—dc21 2002016904 British Library Cataloging-in-Publication Data is available This book has been composed in Galliard and Bulmer Printed on acid-free paper. ∞ pup.princeton.edu Printed in the United States of America 1098765432 Contents ............................................................... PREFACE ix Chapter 1. The Best Way to Travel 1 1.1. Fitness 1 1.2. Speed 2 1.3. Acceleration and Maneuverability 2 1.4. Endurance 4 1.5. Economy of Energy 7 1.6. Stability 8 1.7. Compromises 9 1.8. Constraints 9 1.9. Optimization Theory 10 1.10. Gaits 12 Chapter 2. Muscle, the Motor 15 2.1. How Muscles Exert Force 15 2.2. Shortening and Lengthening Muscle 22 2.3. Power Output of Muscles 26 2.4. Pennation Patterns and Moment Arms 28 2.5. Power Consumption 31 2.6. Some Other Types of Muscle 34 Chapter 3. -

High Ankle Sprains: Diagnosis & Treatment
High Ankle Sprains: Diagnosis & Treatment Mark J. Mendeszoon, DPM, FACFAS, FACFAOM Precision Orthopaedic Specialties University Regional Hospitals Advanced Foot & Ankle Fellowship- Director It Is Only an Ankle Sprain Evaluate Degree of Ecchymosis & Edema If Not Properly Treated Chronic Pain & Ankle Instability Epidemiology Waterman et al. JBJS 2010 states: 2 million ankle sprains per year = 2 billion in health care cost Injury results in time lost and disability in 60% of patients 30% of all sport injury Epidemiology Syndesmotic Injuries: •1% to 18% of all ankle sprains • 32% develop calcification and chronic pain •High incidence of post traumatic arthritis Greater source of impairment than the typical lateral ankle sprain Anatomy Inferior Tibiofibular Joint: defined as a syndesmotic articulation which consists of five separate portions Motion in all three planes Anatomy “Syndesmotic Ligaments: • Anterior Inferior Tibio Fibular Ligament • Posterior Inferior Tibio Fibular Ligament • Transverse Tibio Fibular Ligament • Interosseous Ligament • Interosseous Membrane Deltoid Ligament The deep portion of the deltoid ligament also contributes to syndesmotic stability Acting as a restraint against lateral shift of the talus Biomechanics of Syndesmosis RELEVANT ASPECTS OFANKLE: A considerable clearance takes place between the talus and the distal fibula, which is limited by the tibiofibular syndesmosis With normal stance, almost no twisting and shearing forces act on the ankle joint= static tibfib tension Axial loading tensions AITF and PITF with increase of 10 -17% of body weight intact syndesmosis, the intermalleolar distance increases with dorsiflexion of the talus by 1.0 to 1.25 mm Haraguchi et al. 2009 Intact syndesmosis Fibula ROTATES 2 * externally Equals ~ 2.4 mm distally 0.2-0.4 mm Anterior -posteriorly THUS Fibula moves in 3 D Ogilvie & Harris 1994 Study on Individual Ligaments for Syndesmotic Stability 35% ATIFL 33% TRANSVERSE LIG. -

Knee Pain and Leg-Length Discrepancy After Retrograde Femoral Nailing Ricardo Reina, MD, Fernando E
(aspects of trauma • an original study) Knee Pain and Leg-Length Discrepancy After Retrograde Femoral Nailing Ricardo Reina, MD, Fernando E. Vilella, MD, Norman Ramírez, MD, Richard Valenzuela, MD, Gil Nieves, MD, and Christian A. Foy, MD ABSTRACT an antegrade entry point at the pirifor- MATERIALS AND METHODS We retrospectively studied postop- mis fossa.1,2,4,8-12 This technique has Between October 1998 and April 2000, erative knee function and leg-length several drawbacks, including a dif- a surgeon at University of Puerto Rico discrepancy (LLD) in 31 patients ficult starting point at the piriformis District Hospital and Puerto Rico with femoral diaphyseal fractures fossa, postoperative Trendelenburg Medical Center used retrograde IMN treated with retrograde intramedul- gait, iatrogenic fracture of the femo- to treat 46 femoral shaft fractures con- lary nailing (IMN) between October 1998 and April 2000. Mean follow-up ral neck, need for a fracture table secutively. For the purpose of this study, was 25 months, mean knee range of with difficult patient positioning, and we selected only those fractures motion was 126°, mean Hospital for limitations in use with concomitant located both 5 cm below the lesser Special Surgery knee scores were surgical procedures.3,5,6 trochanter14 and above the femoral 89.2 (pain) and 78.3 (function), and Over the past 20 years, retrograde condyles. Patients were contacted by mean LLD was 1.19 cm. Despite the IMN has emerged as an alternative telephone, by mail, or through local theoretically higher knee pain and that overcomes the shortcomings of government agencies. LLD rates associated with retrograde antegrade IMN in treating femoral Of the 46 patients, 15 (33%) were IMN, we believe it may offer a viable shaft fractures.1,3-5,7,8,13,14 The advan- excluded (4 had passed away, and 11 treatment option when the antegrade nailing technique is restricted.