DOCSLIB.ORG

12 Major Scales for Flute

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
12 Major Scales for Flute Flute 12 Major Scales 1st Octave Concert F Major Scale c F G A Bb C D EF ZASDf/AsdK ZASDf/sddK ZASdf/sddK ZAsdf/ghjK zAsdf/ghjK ZaSDf/GGGk ZASDf/ASdK ZASDf/AsdK Concert Bb Major Scale Bb C D Eb F G A Bb ZAsdf/ghjK zAsdf/ghjK ZaSDf/GGGk ZaSDf/ASAK ZASDf/AsdK ZASDf/sddK ZASdf/sddK ZAsdf/ghjK Concert Eb Major Scale Eb F G Ab Bb C D Eb ZASDf/ASAK ZASDf/AsdK ZASDf/sddK ZASDF/sddK ZAsdf/ghjK zAsdf/ghjK ZaSDf/GGGk ZaSDf/ASAK Concert Ab Major Scale Ab Bb C Db Eb F G Ab ZASDF/sddK ZAsdf/ghjK zAsdf/ghjK xasdf/asdK ZaSDf/ASAK ZASDf/AsdK ZASDf/sddK ZASDF/sddK zasdf/aSDK Enharmonic Scale (lowers pitch) Concert Db (C#) Major Scale Db Eb F Gb Ab Bb C Db xasdf/asdK xasdf/asdK zasdf/aSDK ZaSDf/ASAK ZASDf/AsdK ZASDf/sdAK ZASDF/sddK ZAsdf/ghjK zAsdf/ghjK zasdf/aSDK (lowers pitch) (lowers pitch) C# D# E# F# G# A# B# C# Enharmonic Scale Concert Gb (F#) Major Scale Gb Ab Bb Cb Db Eb F Gb ZASDf/sdAK ZASDF/sddK ZAsdf/ghjK ZaSDf/ASAK ZASDf/AsdK ZASDf/sdAK Thumb position xasdf/asdK determines fingering choice zAsdf/ghjK zasdf/aSDK XASDf/sdAK XASDF/sddK XAsdf/AhjK (lowers pitch) XaSDf/ASAK XASDf/AsdK XASDf/sdAK F# G# A# B C# D# E# F# Copyright © 2020 Flute 2 Enharmonic Scale Concert Cb (B) Major Scale Cb Db Eb Fb Gb Ab Bb Cb zAsdf/ghjK xasdf/asdK ZaSDf/ASAK ZASDf/ASdK ZASDf/sdAK ZASDF/sddK ZAsdf/ghjK zasdf/aSDK zAsdf/ghjK Thumb position (lowers pitch) determines fingering choice XaSDf/ASAK XASDf/ASdK XASDf/sdAK XASDF/sddK XAsdf/AhjK B C# D# EF# G# A# B Concert E Major Scale E F# G# A B C# D# E XASDf/ASdK XASDf/asDK XASDF/sddK XASdf/sddK XAsdf/ghjK xasdf/asdK XaSDf/GGGK XASDf/ASdK zasdf/aSDK (lowers pitch) Concert A Major Scale A B C# D EF# G# A XASdf/sddK XAsdf/ghjK xasdf/asdK XaSDf/GGGk XASDf/ASdK XASDf/asDK XASDF/sddK XASdf/sddK zasdf/aSDK (lowers pitch) Concert D Major Scale D EF# G A B C# D XaSDf/GGGk XASDf/ASdK XASDf/asDK XASDf/sddK XASdf/sddK XAsdf/ghjK xasdf/asdK XaSDf/asdK zasdf/aSDK (lowers pitch) Concert G Major Scale G A B C D EF# G XASDf/sddK XASdf/sddK XAsdf/ghjK zAsdf/ghjK XaSDf/GGGk XASDf/ASdK XASDf/asDK XASDf/sddK ConcertM C Major Scale C D EF G A B C zAsdf/ghjK XaSDf/GGGk XASDf/ASdK XASDf/AsdK XASDf/sddK XASdf/sddK XAsdf/ghjK zAsdf/ghjK Flute 12 Major Scales 3 2nd Octave Concert F Major Scale F G A Bb C D EF ZASDf/AsdK ZASDf/sddK ZASdf/sddK ZAsdf/ghjK zAsdf/ghjK ZaSDf/GGGk ZASdf/ASdK ZAsDf/AsdK ZASdfASdk ZAsDf//AsDK (lowers pitch) (lowers pitch) Concert Bb Major Scale Bb C D Eb F G A Bb ZAsdf/ghjK zAsdf/ghjK ZaSDf/aaak ZASDf/ASAK ZAsDf/AsdK ZASDf/sddK ZaSdf/AddK Zasdf/ABhjk ZAsDf//AsDK ZAsdf/ABsdk Concert Eb Major Scale (lowers pitch) Eb F G Ab Bb C D Eb ZaSDf/ASAK ZASDf/AsdK ZASDf/sddK ZASDF/sddK ZAsdf/ghjK zAsdf/ghjK ZaSDf/asdk ZASDf/ASAK Concert Ab Major Scale Ab Bb C Db Eb F G Ab ZASDF/sddK ZAsdf/ghjK zAsdf/ghjK xasdf/asdK ZASDf/ASAK ZAsDf/AsdK ZASDf/sddK ZASDF/asdK zasdf/aSDK ZAsDf//AsDK ZsSDF//sSDK (lowers pitch) (lowers pitch) (lowers pitch) Enharmonic Scale Concert Db (C#) Major Scale b b b Db Eb F G A B C Db xasdf/asdK ZASDf/sdAK ZAsdf/ghjK zAsdf/ghjK ZASDf/ASAk< ZASDf/ASAK ZASDf/AsdK ZASDF/sddK zasdf/aSDK (lowers pitch) # F# G# A# B# C# C# D# E Enharmonic Scale Concert Gb (F#) Major Scale Gb Ab Bb Cb Db Eb F Gb ZASDf/sdAK ZASDF/sddK ZAsdf/ghjK zAsdf/ghjK xasdf/asdK ZaSDf/ASAK ZAsDf/AsdK ZAsDf/sdDK Thumb position ZAsDf//AsDK ZAsDf//aSdK (lowers pitch) (lowers pitch) determines fingering choice XaSDf/ASAK XASDf/sdAK XASDF/sddK XAsdf/AhjK F# G# A# B C# D# E# F# XAsDf/AsdK XAsDf/sdDK XAsDf//AsDK XAsDf//aSdK (lowers pitch) (lowers pitch) Flute 4 Enharmonic Scale Concert Cb (B) Major Scale Cb Db Eb Fb Gb Ab Bb Cb xasdf/asdK ZaSDf/ASAK ZASDf/ASdK ZASDf/sdAK xaSDF/asdK ZAsdf/ghjK zAsdf/ghjK zAsdf/ghjK zasdf/aSDK zaSDF/aSDK XAsdf/AhjK Thumb position (lowers pitch) XaSDf/ASAK XASDf/ASdK XASDf/sdAK (lowers pitch) determines fingering choice B C# D# EF# G# A# B Concert E Major Scale EF# G# A B C# D# E XASDf/ASdK XASDf/asDK XASDF/sddK XASdf/sddK XAsdf/ghjK xasdf/asdK XASDF/GGGK XASdf/ASdK XASdf/ASdk (lowers pitch) Concert A Major Scale A B C# D EF# G# A XASdf/sddK XAsdf/ghjK xasdf/asdK XaSDf/asdk XASdf/ASdK ZAsDf/sdDK xaSDF/asdK XaSdf/AddK XASdf/ASdk ZAsDf//aSdK zaSDF/aSDK (lowers pitch) (lowers pitch) (lowers pitch) Concert D Major Scale F# G A B C# D D E XASDf/GGGk XASDf/ASdK XASDf/asDK XASDf/sddK XASdf/sddK XAsdf/ghjK xasdf/asdK XaSDf/ASDk zasdf/aSDK (lowers pitch) Concert G Major Scale G A B C D EF# G XASDf/sddK XASdf/sddK XAsdf/ghjK zAsdf/ghjK XaSDf/GGGk XASdf/ASdK ZAsDf/sdDK zASDf/sddK XASdf/ASdk ZAsDf//aSdK (lowers pitch) (lowers pitch) ConcertM C Major Scale F G A B C D E C zAsdf/ghjK XaSDf/GGGk XASDf/ASdK XASDf/AsdK XASDf/sddK XASdf/sddK XAsdf/ghjK zAsdf/ghjK Concert F Chromatic Scale 2 Octave. Flute Going Up 5 F F# G G# A A# ZASDf/AsdK XASDf/asDK ZASDf/sddK XASDF/sddK ZASdf/sddK XAsdf/AhjK B C C# D D# E XAsdf/ghjK zAsdf/ghjK xasdf/asdK XaSDf/GGGk XaSDf/GGGK XASDf/ASdK zasdf/aSDK (lowers pitch) F F# G G# A A# XASDf/AsdK XASDf/asDK XASDf/sddK XASDF/sddK XASdf/sddK XAsdf/AhjK B C C# D D# E XAsdf/ghjK zAsdf/ghjK xasdf/asdK ZaSDf/asdk XASDF/GGGK ZASdf/ASdK ZASdfASdk (lowers pitch) Coming Down F E Eb D Db C ZAsDf/AsdK ZASdf/ASdK ZASDf/ASAK ZaSDf/asdk xasdf/asdK zAsdf/ghjK ZAsDf//AsDK ZASdfASdk zasdf/aSDK (lowers pitch) (lowers pitch) (lowers pitch) BBb A Ab G Gb XAsdf/ghjK XAsdf/AhjK XASdf/sddK ZASDF/sddK XASDf/sddK XASDf/sdAK F E Eb D Db C XASDf/AsdK XASDf/ASdK ZaSDf/ASAK XaSDf/GGGk xasdf/asdK zAsdf/ghjK zasdf/aSDK (lowers pitch) BBb A Ab G Gb F XAsdf/ghjK XAsdf/AhjK ZASdf/sddK ZASDF/sddK ZASDf/sddK XASDf/sdAK ZASDf/AsdK Flute 6 12 Major Scales BONUS SCALE 3rd Octave Concert C Major Scale M C D EF G A B C zAsdf/ghjK XaSDf/asdK XASdf/ASdK XAsDf/AsdK zASDf/sddK XaSdf/AddK XAsAf/ghNjK zASDF/DhjK.
Load more

Recommended publications
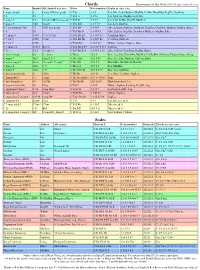
  • Chords and Scales 30/09/18 3:21 PM
    Chords and Scales 30/09/18 3:21 PM Chords Charts written by Mal Webb 2014-18 http://malwebb.com Name Symbol Alt. Symbol (best first) Notes Note numbers Scales (in order of fit). C major (triad) C Cmaj, CM (not good) C E G 1 3 5 Ion, Mix, Lyd, MajPent, MajBlu, DoHar, HarmMaj, RagPD, DomPent C 6 C6 C E G A 1 3 5 6 Ion, MajPent, MajBlu, Lyd, Mix C major 7 C∆ Cmaj7, CM7 (not good) C E G B 1 3 5 7 Ion, Lyd, DoHar, RagPD, MajPent C major 9 C∆9 Cmaj9 C E G B D 1 3 5 7 9 Ion, Lyd, MajPent C 7 (or dominant 7th) C7 CM7 (not good) C E G Bb 1 3 5 b7 Mix, LyDom, PhrDom, DomPent, RagCha, ComDim, MajPent, MajBlu, Blues C 9 C9 C E G Bb D 1 3 5 b7 9 Mix, LyDom, RagCha, DomPent, MajPent, MajBlu, Blues C 7 sharp 9 C7#9 C7+9, C7alt. C E G Bb D# 1 3 5 b7 #9 ComDim, Blues C 7 flat 9 C7b9 C7alt. C E G Bb Db 1 3 5 b7 b9 ComDim, PhrDom C 7 flat 5 C7b5 C E Gb Bb 1 3 b5 b7 Whole, LyDom, SupLoc, Blues C 7 sharp 11 C7#11 Bb+/C C E G Bb D F# 1 3 5 b7 9 #11 LyDom C 13 C 13 C9 add 13 C E G Bb D A 1 3 5 b7 9 13 Mix, LyDom, DomPent, MajBlu, Blues C minor (triad) Cm C-, Cmin C Eb G 1 b3 5 Dor, Aeo, Phr, HarmMin, MelMin, DoHarMin, MinPent, Ukdom, Blues, Pelog C minor 7 Cm7 Cmin7, C-7 C Eb G Bb 1 b3 5 b7 Dor, Aeo, Phr, MinPent, UkDom, Blues C minor major 7 Cm∆ Cm maj7, C- maj7 C Eb G B 1 b3 5 7 HarmMin, MelMin, DoHarMin C minor 6 Cm6 C-6 C Eb G A 1 b3 5 6 Dor, MelMin C minor 9 Cm9 C-9 C Eb G Bb D 1 b3 5 b7 9 Dor, Aeo, MinPent C diminished (triad) Cº Cdim C Eb Gb 1 b3 b5 Loc, Dim, ComDim, SupLoc C diminished 7 Cº7 Cdim7 C Eb Gb A(Bbb) 1 b3 b5 6(bb7) Dim C half diminished Cø
    [Show full text]
  • Major and Minor Scales Half and Whole Steps
    Dr. Barbara Murphy University of Tennessee School of Music MAJOR AND MINOR SCALES HALF AND WHOLE STEPS: half-step - two keys (and therefore notes/pitches) that are adjacent on the piano keyboard whole-step - two keys (and therefore notes/pitches) that have another key in between chromatic half-step -- a half step written as two of the same note with different accidentals (e.g., F-F#) diatonic half-step -- a half step that uses two different note names (e.g., F#-G) chromatic half step diatonic half step SCALES: A scale is a stepwise arrangement of notes/pitches contained within an octave. Major and minor scales contain seven notes or scale degrees. A scale degree is designated by an Arabic numeral with a cap (^) which indicate the position of the note within the scale. Each scale degree has a name and solfege syllable: SCALE DEGREE NAME SOLFEGE 1 tonic do 2 supertonic re 3 mediant mi 4 subdominant fa 5 dominant sol 6 submediant la 7 leading tone ti MAJOR SCALES: A major scale is a scale that has half steps (H) between scale degrees 3-4 and 7-8 and whole steps between all other pairs of notes. 1 2 3 4 5 6 7 8 W W H W W W H TETRACHORDS: A tetrachord is a group of four notes in a scale. There are two tetrachords in the major scale, each with the same order half- and whole-steps (W-W-H). Therefore, a tetrachord consisting of W-W-H can be the top tetrachord or the bottom tetrachord of a major scale.
    [Show full text]
  • When the Leading Tone Doesn't Lead: Musical Qualia in Context
    When the Leading Tone Doesn't Lead: Musical Qualia in Context Dissertation Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio State University By Claire Arthur, B.Mus., M.A. Graduate Program in Music The Ohio State University 2016 Dissertation Committee: David Huron, Advisor David Clampitt Anna Gawboy c Copyright by Claire Arthur 2016 Abstract An empirical investigation is made of musical qualia in context. Specifically, scale-degree qualia are evaluated in relation to a local harmonic context, and rhythm qualia are evaluated in relation to a metrical context. After reviewing some of the philosophical background on qualia, and briefly reviewing some theories of musical qualia, three studies are presented. The first builds on Huron's (2006) theory of statistical or implicit learning and melodic probability as significant contributors to musical qualia. Prior statistical models of melodic expectation have focused on the distribution of pitches in melodies, or on their first-order likelihoods as predictors of melodic continuation. Since most Western music is non-monophonic, this first study investigates whether melodic probabilities are altered when the underlying harmonic accompaniment is taken into consideration. This project was carried out by building and analyzing a corpus of classical music containing harmonic analyses. Analysis of the data found that harmony was a significant predictor of scale-degree continuation. In addition, two experiments were carried out to test the perceptual effects of context on musical qualia. In the first experiment participants rated the perceived qualia of individual scale-degrees following various common four-chord progressions that each ended with a different harmony.
    [Show full text]
  • HOW to FIND RELATIVE MINOR and MAJOR SCALES Relative
    HOW TO FIND RELATIVE MINOR AND MAJOR SCALES Relative minor and major scales share all the same notes–each one just has a different tonic. The best example of this is the relative relationship between C-major and A-minor. These two scales have a relative relationship and therefore share all the same notes. C-major: C D E F G A B C A-minor: A B C D E F G A Finding the relative minor from a known major scale (using the 6th scale degree) scale degrees: 1 2 3 4 5 6 7 1 C-major: C D E F G A B C A-(natural) minor: A B C D E F G A A-minor starts on the 6th scale degree of C-major. This relationship holds true for ALL major and minor scale relative relationships. To find the relative minor scale from a given major scale, count up six scale degrees in the major scale–that is where the relative minor scale begins. This minor scale will be the natural minor mode. 1 2 3 4 5 6 C-D-E-F-G-A The relative minor scale can also be found by counting backwards (down) by three scale degrees in the major scale. C-major: C D E F G A B C ←←← count DOWN three scale degrees and arrive at A 1 2 3 C-B-A Finding the relative major from a known minor scale (using the 3rd scale degree) scale degrees: 1 2 3 4 5 6 7 1 A-(natural) minor: A B C D E F G A C-major: C D E F G A B C C-major starts on the 3rd scale of A-minor.
    [Show full text]
  • The Worlds of Rigoletto: Verdiâ•Žs Development of the Title Role in Rigoletto
    Florida State University Libraries Electronic Theses, Treatises and Dissertations The Graduate School 2008 The Worlds of Rigoletto Verdi's Development of the Title Role in Rigoletto Mark D. Walters Follow this and additional works at the FSU Digital Library. For more information, please contact [email protected] THE FLORIDA STATE UNIVERSITY COLLEGE OF MUSIC THE WORLDS OF RIGOLETTO VERDI’S DEVELOPMENT OF THE TITLE ROLE IN RIGOLETTO By MARK D. WALTERS A Treatise submitted to the College of Music in partial fulfillment of the requirements for the degree of Doctor of Music Degree Awarded: Spring Semester, 2008 The members of the Committee approve the Treatise of Mark D. Walters defended on September 25, 2007. Douglas Fisher Professor Directing Treatise Svetla Slaveva-Griffin Outside Committee Member Stanford Olsen Committee Member The Office of Graduate Studies has verified and approved the above named committee members. ii I would like to dedicate this treatise to my parents, Dennis and Ruth Ann Walters, who have continually supported me throughout my academic and performing careers. iii ACKNOWLEDGEMENTS I would like to express my gratitude to Professor Douglas Fisher, who guided me through the development of this treatise. As I was working on this project, I found that I needed to raise my levels of score analysis and analytical thinking. Without Professor Fisher’s patience and guidance this would have been very difficult. I would like to convey my appreciation to Professor Stanford Olsen, whose intuitive understanding of musical style at the highest levels and ability to communicate that understanding has been a major factor in elevating my own abilities as a teacher and as a performer.
    [Show full text]
  • Nietzsche, Debussy, and the Shadow of Wagner
    NIETZSCHE, DEBUSSY, AND THE SHADOW OF WAGNER A Dissertation Presented to the Faculty of the Graduate School of Cornell University in Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy by Tekla B. Babyak May 2014 ©2014 Tekla B. Babyak ii ABSTRACT NIETZSCHE, DEBUSSY, AND THE SHADOW OF WAGNER Tekla B. Babyak, Ph.D. Cornell University 2014 Debussy was an ardent nationalist who sought to purge all German (especially Wagnerian) stylistic features from his music. He claimed that he wanted his music to express his French identity. Much of his music, however, is saturated with markers of exoticism. My dissertation explores the relationship between his interest in musical exoticism and his anti-Wagnerian nationalism. I argue that he used exotic markers as a nationalistic reaction against Wagner. He perceived these markers as symbols of French identity. By the time that he started writing exotic music, in the 1890’s, exoticism was a deeply entrenched tradition in French musical culture. Many 19th-century French composers, including Felicien David, Bizet, Massenet, and Saint-Saëns, founded this tradition of musical exoticism and established a lexicon of exotic markers, such as modality, static harmonies, descending chromatic lines and pentatonicism. Through incorporating these markers into his musical style, Debussy gives his music a French nationalistic stamp. I argue that the German philosopher Nietzsche shaped Debussy’s nationalistic attitude toward musical exoticism. In 1888, Nietzsche asserted that Bizet’s musical exoticism was an effective antidote to Wagner. Nietzsche wrote that music should be “Mediterranized,” a dictum that became extremely famous in fin-de-siècle France.
    [Show full text]
  • The Major Scale Music Sounds the Way It Does Has to Do with the Group of Notes the Composer Decided to Use
    music theory for musicians and normal people by toby w. rush one of the reasons that a particular piece of The Major Scale music sounds the way it does has to do with the group of notes the composer decided to use. 2 2 , 17 bach na e bachr a magdal ian jo t a ann bas m G for se n i ann ook oh eb inuett j M no œ#œ œ œ œ œ œ &43 œ œ œ œ œ œ œœœ œ œ œ œ œ œ œ œ œ œ œ œ œ œ ˙. take this melody, for example... let’s first remove all the duplicate notes, regardless of which octave they’re in. œ#œ œ &43 œ œ œ œ next, let’s put the notes in alphabetical order, œ #œ œ starting on the note œ #œ œ œ œ œ that the melody sounded œ œ œ œ like it was centering on. œ œ what we end up with there are actually many is the for “palette” different types of scales, this particular piece... each with a different pattern of whole steps and half steps. œ œ œ #œ œ œ œ œ a half step is the distance between like the board on which a painter holds two adjacent keys the bits of paint being used in the painting on the piano keyboard, being created. regardless of color. in music, this “palette” is called a scale. though we usually write scales from low to high, the order is actually unimportant; it’s the notes contained in the scale that help make a piece sound the way it does.
    [Show full text]
  • 11-Music Scales
    Scales in Music Gary Hardegree Department of Philosophy University of Massachusetts Amherst, MA 01003 1. Introduction......................................................................................................................................1 2. The Fundamental Unit – The Octave...............................................................................................2 1. An Aside on Logarithmic Scales .........................................................................................5 2. Cents and Sensibility............................................................................................................6 3. The Pythagorean Construction of the Major Scale..........................................................................7 4. Ptolemaic Tuning...........................................................................................................................10 5. Mean-Tone Temperament (Tuning by Major Thirds) ...................................................................11 6. Problems with Perfect Tuning........................................................................................................12 1. An Aside on The Circle of Fifths and the Circle of Thirds................................................14 2. Back to the Problem of Tuning by Fifths...........................................................................14 3. Ptolemaic Tuning Makes Matters Even Worse! ................................................................15 4. Mean-Tone Temperament’s Wolves..................................................................................17
    [Show full text]
  • Finding Alternative Musical Scales
    Finding Alternative Musical Scales John Hooker Carnegie Mellon University October 2017 1 Advantages of Classical Scales • Pitch frequencies have simple ratios. – Rich and intelligible harmonies • Multiple keys based on underlying chromatic scale with tempered tuning. – Can play all keys on instrument with fixed tuning. – Complex musical structure. • Can we find new scales with these same properties? – Constraint programming is well suited to solve the problem. 2 Simple Ratios • Acoustic instruments produce multiple harmonic partials. – Frequency of partial = integral multiple of frequency of fundamental. – Coincidence of partials makes chords with simple ratios easy to recognize. Perfect fifth C:G = 2:3 3 Simple Ratios • Acoustic instruments produce multiple harmonic partials. – Frequency of partial = integral multiple of frequency of fundamental. – Coincidence of partials makes chords with simple ratios easy to recognize. Octave C:C = 1:2 4 Simple Ratios • Acoustic instruments produce multiple harmonic partials. – Frequency of partial = integral multiple of frequency of fundamental. – Coincidence of partials makes chords with simple ratios easy to recognize. Major triad C:E:G = 4:5:6 5 Multiple Keys • A classical scale can start from any pitch in a chromatic with 12 semitone intervals. – Resulting in 12 keys. – An instrument with 12 pitches (modulo octaves) can play 12 different keys. – Can move to a different key by changing only a few notes of the scale. 6 Multiple Keys Let C major be the tonic key C 1 D#E 6 A C major b 0 notes F#G
    [Show full text]
  • In Search of the Perfect Musical Scale
    In Search of the Perfect Musical Scale J. N. Hooker Carnegie Mellon University, Pittsburgh, USA [email protected] May 2017 Abstract We analyze results of a search for alternative musical scales that share the main advantages of classical scales: pitch frequencies that bear simple ratios to each other, and multiple keys based on an un- derlying chromatic scale with tempered tuning. The search is based on combinatorics and a constraint programming model that assigns frequency ratios to intervals. We find that certain 11-note scales on a 19-note chromatic stand out as superior to all others. These scales enjoy harmonic and structural possibilities that go significantly beyond what is available in classical scales and therefore provide a possible medium for innovative musical composition. 1 Introduction The classical major and minor scales of Western music have two attractive characteristics: pitch frequencies that bear simple ratios to each other, and multiple keys based on an underlying chromatic scale with tempered tuning. Simple ratios allow for rich and intelligible harmonies, while multiple keys greatly expand possibilities for complex musical structure. While these tra- ditional scales have provided the basis for a fabulous outpouring of musical creativity over several centuries, one might ask whether they provide the natural or inevitable framework for music. Perhaps there are alternative scales with the same favorable characteristics|simple ratios and multiple keys|that could unleash even greater creativity. This paper summarizes the results of a recent study [8] that undertook a systematic search for musically appealing alternative scales. The search 1 restricts itself to diatonic scales, whose adjacent notes are separated by a whole tone or semitone.
    [Show full text]
  • Modulation: Pivot Chords
    MODULATION: PIVOT CHORDS APPLICATIONS OF THE HARMONIC WHEEL CONTENTS 2 The Modulation consists in changing from one Key to another. To do that, it is common to use a Pivot Chord, which is a chord that belongs to both keys, and then the new key is affirmed by a Cadence, which may consist, simply, in the chords V7 I. In this presentation, an explanation is given on how to obtain the pivot chords between two keys, using the Harmonic Wheel. For the sake of simplicity, only consonant pivot chords are considered, that is, Major or minor. © 2009 www.harmonicwheel.com CHORDS OF A GIVEN KEY 3 Every Major or natural minor key contains 6 consonant chords: 3 Major and 3 minor. On the Harmonic Wheel, these 6 chords are inside a curved rectangle and they are placed taking into account their affinity. For example, in the C Major / A minor key these 6 chords appear in the following arrangement: Dm Am Em F C G © 2009 www.harmonicwheel.com CHORDS OF A GIVEN KEY 4 © 2009 www.harmonicwheel.com CHORDS OF A GIVEN KEY 5 Remember that the scale tonic is indicated with and the rest of the notes with . Traditionally, the modulation is studied with the aid of the cycle of fifths, where the keys are sorted according to their key signatures. On its own, the Harmonic Wheel is a much more complete representation than a cycle of fifths, since it gives a panoramic view of chords and keys, as well as the existing relationships among them. © 2009 www.harmonicwheel.com MODUL.
    [Show full text]
  • Natural Minor Scale Is Given
    Minor Scales Minor scales/keys are used by composers when they wish to express a different mood than those characterized my major scales in music. Minor scales and keys conjure feelings of sorrow or tension. Minor scales also have their own unique set of intervals found between the 8 pitches in the scale. The major scale which used all white notes on the piano is the C major scale (example #1). Example #1 q Q Q l=============& _q q q q l q =l[ The minor scale which uses all white notes on the piano the scale with no sharps or flats is A minor. The C major scale and the A minor scale are related (they are cousins) because they share the same key signature, no sharps or flats. Example #2 shows that relationship very clearly. All of notes in the A minor scale are found in the C major scale with the difference between the two just the starting note or tonic. The C major scale starts on C which is its tonic and the A minor scale starts on A which is its tonic. Example #2 Î Î q Q Q Major l===============& _q q lq q q l =l[ l l q q q Î Î Minor l===============& _q _q _q q l q l =l[ The unique relationship of major and minor makes the work of studying minor simpler. As we know from the information above each major scale/key has a relative (cousin) minor that uses the same notes and key signatures however each starts on a different note (tonic).
    [Show full text]