DOCSLIB.ORG

PRICING of SWING OPTIONS: a MONTE CARLO SIMULATION APPROACH a Dissertation Submitted to Kent State University in Partial Fulfill

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
PRICING of SWING OPTIONS: a MONTE CARLO SIMULATION APPROACH a Dissertation Submitted to Kent State University in Partial Fulfill PRICING OF SWING OPTIONS: A MONTE CARLO SIMULATION APPROACH A dissertation submitted to Kent State University in partial fulfillment of the requirements for the degree of Doctor of Philosophy by Kai-Siong Leow May, 2013 Dissertation written by Kai-Siong Leow B.S., Iowa State University, 1998 M.S., Oklahoma State University, 2003 Ph.D., Kent State University, 2013 Approved by , Chair, Doctoral Dissertation Committee Dr. Oana Mocioalca , Member, Doctoral Dissertation Committee Dr. Mohammad Kazim Khan , Member, Doctoral Dissertation Committee Dr. Lothar Reichel , Member, Outside Discipline Dr. Maxim Dzero , Member, Graduate Faculty Representative Dr. Eric Johnson Accepted by , Chair, Department of Mathematical Sciences Dr. Andrew Tonge , Associate Dean, College of Arts and Sciences Dr. Raymond A. Craig ii TABLE OF CONTENTS LIST OF FIGURES ......................................... v ACKNOWLEDGEMENTS ..................................... vi 1 Introduction ............................................ 1 1.1 Literature Review ..................................... 1 1.2 Derivative Pricing in Incomplete Market ......................... 3 1.3 Calibration of Energy Spot Price Process ........................ 8 1.4 Organization of the Dissertation ............................. 12 2 Model Description and Formulation ............................... 14 2.1 Swing Optionality ..................................... 14 2.2 Definition of Swing Options ................................ 17 2.3 Stochastic Optimal Control Model ............................ 18 2.4 Dynamic Programming Formulation ........................... 23 2.5 Structural Properties of Optimal Value Functions .................... 26 3 Monte Carlo Pricing Algorithm and Its Convergence ..................... 36 3.1 A Monte Carlo Simulation Method ............................ 36 3.2 Convergence of the Algorithm ............................... 43 3.3 Technical Lemmas ..................................... 48 3.4 Convergence Proof ..................................... 69 4 Numerical Results ........................................ 73 4.1 Swing Call Option ..................................... 73 BIBLIOGRAPHY .......................................... 80 iii A Bootstrapping the Risk-Free Discount Curve .......................... 83 A.1 Cash Deposit on Fed Funds Effective Rate ........................ 85 A.2 OIS Swap .......................................... 85 A.3 Synthetic OIS Swap: Fed Funds/3M LIBOR Basis Swap + 3M LIBOR Swap . 87 A.4 Bootstrapping Algorithm ................................. 88 B The MATLAB code ....................................... 90 C Optimal Exercise Strategy of the Swing Call Option in Section 4.1 ............. 105 iv LIST OF FIGURES 1.1 Monthly NYMEX Natural Gas Futures prices, open interests and trading volumes as of 2:30pm EST, 23 January 2013. Copyright 2013 Bloomberg Finance L.P. Reprinted with permission. All right reserved. Visit www.Bloomberg.com. ............ 9 1.2 Henry Hub natural gas spot price from 5th January 2011 to 23rd January 2013 . 11 1.3 Linear regression on logarithmic spot prices ....................... 12 2.1 System dynamics at t = 0 ................................. 20 2.2 System dynamics at a generic time t ........................... 21 2.3 System dynamics at T ................................... 21 2.4 Optimal value functions at T ............................... 23 2.5 Optimal value functions at a generic time t ....................... 24 2.6 Optimal value functions at t = 0 ............................. 25 4.1 Simulation of Schwartz One-Factor Mean Reverting Process .............. 74 4.2 Option Price Computed by Policy Generated at Each Iterate. ............. 75 4.3 50,000 paths of cumulative quantity exercised through time .............. 77 4.4 86 price scenarios where cumulative quantity at expiry exceed Rmax. ......... 77 4.5 115 price scenarios where cumulative quantity at expiry of the holder is less than Rmin. 78 4.6 Option prices by strikes and penalties .......................... 78 v ACKNOWLEDGEMENTS My most earnest acknowledgement must go to my advisor, Professor Oana Mocioalca, for her guidance, support, encouragement, patience and enthusiasm for this research. Thank you very much! My graduate studies at Kent State has been a wonderful experience. Thanks to the necessary and sufficient financial support that the mathematics department had provided for the first four years of my graduate studies. I would like to extend my thanks to the following individuals at Kent State who have been supportive and/or taught me different areas of mathematics in the past: Dr. Kazim Khan, Dr. Lothar Reichel, Dr. Chuck Gartland, Dr. Hassan Allouba, Dr. Mikhail Chebotar, Dr. Joe Diestel, Dr. Beverly Reed, Ms. Misty Sommers-Tackett, Ms. Virginia Wright, Dr. Volodymyr Andriyevskyy, Dr. Jing Li, Dr. Artem Zvavitch and Dr. Andrew Tonge. Also, I would like to thank my professors at Oklahoma State: Dr. Dale Alspach and Dr. William (Bus) Jaco; and Iowa State: Dr. Stephen Willson. A respectful thanks to Dr. Jaco for showing me the beautiful world of three dimensional manifold topology. I enjoyed your geometric and algebraic topology classes very much. Thanks to all of my colleagues at work. Through collaboration of projects, model validations, maintaining data quality and fixing market risk system issues, you helped improve my risk mea- surement skills. Thanks to Mr. William Kugler, Dr. Vilen Abramov and Dr. Dennis Jarecke for bringing me onboard to the banking industry. Thanks to Mr. Don Schilling, you are a great boss. Thanks to Pastor Huang, Sister Gu and members from the church for your guidance and prayers. With love and gratitude, I give thanks to my father, Peter Leow, and mother, Susan Soo, for all that you gave me. Thanks to my sisters for your emotional support and helps taking care of our mother after the recent untimely departure of our father due to terminal illness. Father, I just wanted to say that I love you and that you are always in my memory. I will continue to work hard, take care of the family and live up to your expectation. My special thanks go to my wife Winnie. You take good care of our adorable daughter, Christy so that I can stay focus on my research and work. Thank you for your love. Thanks to my little Christy for the joy you bring to my life. Also, thanks to my soon-to-be born son Aaron for the late March/early April deadline you have set for me to finish this dissertation. vi Thanks to God for all the blessings you bring to me and my family! vii CHAPTER 1 Introduction We study the problem of pricing swing options, a class of multiple early exercise options that are traded in energy market, particularly in the natural gas and electricity markets. These contracts permit the option holder to periodically exercise the right to trade a variable amount of energy with a counterparty, subject to local volumetric constraints. In addition, the total amount of energy traded from settlement to expiration with the counterparty is restricted by a global volumetric constraint. Violation of this global volumetric constraint is allowed but would lead to penalty settled at expiration. The pricing problem is formulated as a stochastic optimal control problem in discrete time and state space. We present a stochastic dynamic programming algorithm which is based on piecewise linear concave approximation of value functions. This algorithm yields the value of the swing option under the assumption that the optimal exercise policy is applied by the option holder. It is well known that the price of an American option, which is a variant of swing option, has no closed-form formula. Therefore finding a closed-form formula for swing option is unlikely and we have to resort to numerical methods for approximating its price. Numerical techniques employed generally fall into one of the followings: lattice/tree, numerical partial differential equations (PDE), and Monte Carlo simulation. 1.1 Literature Review The first paper on pricing swing option is the paper by Thompson [54], who used a binomial tree algorithm to price take-or-pay contracts, a version of swing options. The paper assumed a simple one-factor geometric Brownian motion in the spot price process. Lari-Lavassani et al. [34] developed another binomial tree whose spot price is a two-factor mean reverting process. Jaillet et al.[27] however employed a trinomial tree for pricing swing options written on natural gas. In PDE- based approach, Kjaer [31] prices electricity swing options for a jump-diffusion spot (day-ahead) price process using finite difference method to solve a partial integro-differential equation. Wilhelm 1 2 [55] uses finite elements. A drawback of lattice-based and PDE-based methods is that an exogenous price process in the form of stochastic differential equation must be specified, similar to models used in financial markets. However, certain energy derivative practitioners are more in favor of fundamental market models for the price process. Unlike spot or forward price models in financial markets that focus on answering the question of how price moves, the fundamental market model looks beyond prices and attempts to answer the question of what causes the price movement. For example, the fundamental market model in Burger et al. [17] is a spot price model comprised of a seasonal autoregressive integrative moving average (SARIMA) forecast of the system load, a deterministic function which specifies the expected relative availability of power plants, an estimate of the price-load
Load more

Recommended publications
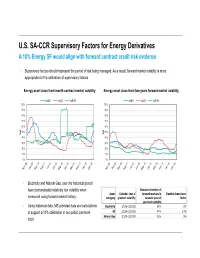
  • U.S. SA-CCR Supervisory Factors for Energy Derivatives a 10% Energy SF Would Align with Forward Contract Credit Risk Evidence
    U.S. SA-CCR Supervisory Factors for Energy Derivatives A 10% Energy SF would align with forward contract credit risk evidence • Supervisory factors should represent the period of risk being managed. As a result, forward market volatility is more appropriate for the calibration of supervisory factors Energy asset class front month contract market volatility Energy asset class front two years forward market volatility VolNG VolOil VolPJM VolNG VolOil VolPJM 100% 100% 90% 90% 80% 80% 70% 70% 60% 60% 50% 50% Vol Vol 40% 40% 30% 30% 20% 20% 10% 10% 0% 0% • Electricity and Natural Gas, over the historical period have demonstrated relatively low volatility when Standard deviation of Asset Calendar year of forward markets in Implied Supervisory measured using forward market history. category greatest volatility calendar year of Factor greatest volatility • Using historical data, MS provided data and calculations Electricity 1/1/08-12/31/08 24% 6% to support a 10% calibration in our public comment Oil 1/1/08-12/31/08 47% 13% Natural Gas 1/1/09-12/31/09 32% 9% letter 1 U.S. SA-CCR Supervisory Factors for Energy Derivatives A 10% Energy SF would align with credit risk in energy derivative transactions 1. Cal18 WTI Swap Pricing: Notional BBLs x Cal18 Prices 2. Cal18 WTI MTM vs SA-CCR vs Mean Positive Exposure 150 90 Oil 1 0 /12 450 1 /10 80 1 1 100 /11 /8 1 1 350 /9 /6 70 1 1 /7 /4 1 1 50 /5 /2 60 250 1 1 /3 50 - $MM 150 $MM 40 $/BBL 50 (50) 30 20 -50 (100) 10 -150 (150) 0 Cal18 MTM SA-CCR RWA Exposure at 40% SF Cal18 MTM ($MM) Notional Quantity (BBLs) * SA-CCR RWA Exposure at 10% SF Max Mean Positive Exposure Cal18 Price ($/BBL) 1/# Spot Contribution to MTM • Energy derivative counterparty credit risk exposures decline, • A 10% Supervisory Factor correctly aligns SA-CCR month by month, as the transaction nears maturity since the credit risk measurements with other reliable counterparty remaining total notional quantity declines credit risk measures (i.e.
    [Show full text]
  • Derivatives and Risk Management in the Petroleum, Natural Gas, and Electricity Industries
    SR/SMG/2002-01 Derivatives and Risk Management in the Petroleum, Natural Gas, and Electricity Industries October 2002 Energy Information Administration U.S. Department of Energy Washington, DC 20585 This report was prepared by the Energy Information Administration, the independent statistical and analytical agency within the U.S. Department of Energy. The information contained herein should be attributed to the Energy Information Administration and should not be construed as advocating or reflecting any policy position of the Department of Energy or any other organization. Service Reports are prepared by the Energy Information Administration upon special request and are based on assumptions specified by the requester. Contacts This report was prepared by the staff of the Energy The Energy Information Administration would like to Information Administration and Gregory Kuserk of the acknowledge the indispensible help of the Commodity Commodity Futures Trading Commission. General Futures Trading Commission in the research and writ- questions regarding the report may be directed to the ing of this report. EIA’s special expertise is in energy, not project leader, Douglas R. Hale. Specific questions financial markets. The Commission assigned one of its should be directed to the following analysts: senior economists, Gregory Kuserk, to this project. He Summary, Chapters 1, 3, not only wrote sections of the report and provided data, and 5 (Prices and Electricity) he also provided the invaluable professional judgment Douglas R. Hale and perspective that can only be gained from long expe- (202/287-1723, [email protected]). rience. The EIA staff appreciated his exceptional pro- ductivity, flexibility, and good humor.
    [Show full text]
  • Long-Term Swings and Seasonality in Energy Markets Working Paper Nº 1929
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by EPrints Complutense Long-term swings and seasonality in energy markets Instituto Manuel Moreno Complutense Department of Economic Analysis and Finance, University of Castilla-La Mancha, Toledo, Spain de Análisis Económico Alfonso Novales Instituto Complutense de Análisis Económico (ICAE), and Department of Economic Analysis, Facultad de Ciencias Económicas y Empresariales, Universidad Complutense, Madrid, Spain Federico Platania Léonard de Vinci Pôle Universitaire, Paris La Défense, France Abstract This paper introduces a two-factor continuous-time model for commodity pricing under the assumption that prices revert to a stochastic mean level, which shows smooth, periodic fluctuations over long periods of time. We represent the mean reversion price by a Fourier series with a stochastic component. We also consider a seasonal component in the price level, an essential characteristic of many commodity prices, which we represent again by a Fourier series. We obtain analytical pricing expressions for futures contracts. Using futures price data on Natural Gas, we provide evidence on the presence of long-term fluctuations and show how to estimate the long-term component simultaneously with a seasonal component using the Kalman filter. We analyse the in-sample and out-of-sample empirical performance of our pricing model with and without a seasonal component and compare it with the Schwartz and Smith (2000) model. Our findings show the in-sample and out-of-sample superiority of our model with seasonal fluctuations, thereby providing a simple and powerful tool for portfolio management, risk management, and derivative pricing.
    [Show full text]
  • The Impact of Energy Derivatives on the Crude Oil Market
    THE JAMES A. BAKER III INSTITUTE FOR PUBLIC POLICY OF RICE UNIVERSITY THE IMPACT OF ENERGY DERIVATIVES ON THE CRUDE OIL MARKET JEFF FLEMING ASSISTANT PROFESSOR OF FINANCE JONES SCHOOL OF MANAGEMENT, RICE UNIVERSITY BARBARA OSTDIEK ASSISTANT PROFESSOR OF FINANCE JONES SCHOOL OF MANAGEMENT, RICE UNIVERSITY THE IMPACT OF ENERGY DERIVATIVES ON THE CRUDE OIL MARKET Introduction Beginning in the 1970s, deregulation dramatically increased the degree of price uncertainty in the energy markets, prompting the development of the first exchange- traded energy derivative securities. The success and growth of these contracts attracted a broader range of participants to the energy markets and stimulated trading in an even wider variety of energy derivatives. Today, many exchanges and over-the-counter markets worldwide offer futures, futures options, swap contracts, and exotic options on a broad range of energy products, including crude oil, fuel oil, gasoil, heating oil, unleaded gasoline, and natural gas. It is well known that derivative securities provide economic benefits. The key attribute of these securities is their leverage (i.e., for a fraction of the cost of buying the underlying asset, they create a price exposure similar to that of physical ownership). As a result, they provide an efficient means of offsetting exposures among hedgers or transferring risk from hedgers to speculators. In addition, derivatives promote information dissemination and price discovery. The leverage and low trading costs in these markets attract speculators, and as their presence increases, so does the amount of information impounded into the market price. These effects ultimately influence the underlying commodity price through arbitrage activity, leading to a more broadly based market in which the current price corresponds more closely to its true value.
    [Show full text]
  • Energy Derivatives and Risk Management
    Department of Business and Management Master thesis in Advanced Corporate Finance ENERGY DERIVATIVES AND RISK MANAGEMENT SUPERVISOR: CANDIDATE: Prof. Raffaele Oriani Alessia Gidari 643081 CO-SUPERVISOR: Prof. Simone Mori ACADEMIC YEAR 2012-2013 1 Table of contents Abstract ...........................................................................................................................4 Introduction......................................................................................................................5 1. Risk management 1.1. A brief historical background……………………………………………………………….9 1.2. Risk definition and measurement……………………………………………………….10 1.3. The risk in corporate finance……………………………………………………………….12 1.4. The reasons for hedging……………………………………………………………………..13 1.5. The risk in capital investment……………………………………………………………..15 1.6. From hedging to risk management……………………………………………………..17 2. Enterprise risk management 2.1. Definition……………………………………………………………………………………………19 2.2. Implementation………………………………………………………………………………….20 2.3. Case studies in literature…………………………………………………………………….23 2.4. Empirical observations………………………………………………………………………..26 2.5. Evolution of risk management…………………………………………………………….32 3. The quantitative tools of risk management 3.1. The Black-Scholes model…………………………………………………………………….35 3.2. The main VaR methodologies……………………………………………………………..37 3.2.1. The historical simulation…………………………………………………………38 3.2.2. The Variance-covariance or analytical method……………………….39 3.2.3. The Monte Carlo method………………………………………………………..41
    [Show full text]
  • A Market Consistent Gas Storage Modelling Framework: Valuation, Calibration, & Model Risk
    A Market Consistent Gas Storage Modelling Framework: Valuation, Calibration, & Model Risk by Greg Kiely B.Sc, National University of Ireland, Galway, (1st Hons.) M.Sc University of Limerick, (1st Hons.) Submitted to the Department of Accounting and Finance, Kemmy Business School, University of Limerick in December 2015, in partial fulfillment of the requirements for the degree of Doctor of Philosophy Abstract A typical natural gas derivatives book within an energy trading business, bank, or even large utility will generally be exposed to two broad categories of market risk. The first being outright price volatility, where contracts such as caps/floors, options and swing, will have a non-linear exposure to the variability of the gas price level. The second, although equally as prominent, is time-spread volatility where gas storage, take-or-pay contracts, and calendar spread options will be exposed to the realized variability of different time-spreads. Developing a market consistent valuation framework capable of capturing both risk exposures, and thus allowing for risk diversification within a natural gas trading book, is the primary goal of this thesis. To accomplish this, we present a valuation methodology which is capable of pricing the two most actively traded natural gas derivative contracts, namely monthly options and storage, in a consistent manner. The valuation of the former is of course trivial as the prices are set by the market, therefore the primary focus of this thesis is in obtaining market-based pricing measures for the purpose of storage valuation. A consistent pricing and risk management framework will, by definition, accurately reflect the cost of hedging both outright and spread volatility and thus our work can be viewed as a ba- sis capable of incorporating the other less actively traded contracts listed above.
    [Show full text]
  • 18. Energy Futures Markets for Managing Risk
    Self Test Energy Futures Markets for Managing Risk Click on True or False to test your knowledge of the chapter. 1. True False Riskiness of the energy industry is perceived as a "chance of loss" in the popular sense. 2. True False Financial risk includes the possibility of accidents that have health and safety implications, examples such as power plant melt down, oil spill, an LNG explosion, smog etc. 3. True False There are six types of financial risk including market, credit, premium, liquidity, operational, and legal. 4. True False A risk neutral individual would be indifferent between $200 and an asset that has 20% chance of paying $1000 and 80% chance of paying nothing. 5. True False To find the optimal hedge ratio (the ratio which minimizes risk or variance), we T use the following formula: δ = ρ + μ+ (lnSt - lnFt )/T. 6. True False The efficient market hypothesis suggests that the spot price plus any necessary risk premium (RP) is a good predictor of future energy prices. 7. True False A derivative is a financial instrument whose value depends on the value of an underlying asset. 8. True False Suppose you have purchased a futures contract of 1,000 barrels for $35/bbl for June delivery and you have posted a margin of $3400, and the price of crude for June delivery increases to $35.50 tomorrow, and you decide to cash out tomorrow. Your margin will increase to $3900, and if you decide to cash out, you will have $500 less a transaction fee. 9. True False High volatility of energy prices since 1973 is one of the reasons that drove the development of financial derivative markets.
    [Show full text]
  • Energy and Power Risk Management
    Additional Praise for Energy and Power Risk Management “Eydeland and Wolyniec give a very detailed, yet quite readable, presenta- tion of the risk management tools in energy markets. The book will be a valuable resource for anyone studying or participating in energy markets.” —Severin Borenstein E.T. Grether Professor of Business Administration and Public Policy, Haas School of Business, University of California, Berkeley Director, University of California Energy Institute “Activity in the power sector exposes all participants to complex and unique risk. Deregulation and the collapse of Enron have only increased the need to understand and control these risks. Covering the spectrum of risk and valu- ation, from the fundamentals of price movement and modeling with poor data, to physical asset valuation and the complex energy derivatives, this book offers a firm foundation from which to solve real world problems.” —Dr. Chris Harris General Manager, Commercial Operations, InnogyOne Founded in 1807, John Wiley & Sons is the oldest independent publishing company in the United States. With offices in North America, Europe, Aus- tralia, and Asia, Wiley is globally committed to developing and marketing print and electronic products and services for our customers’ professional and personal knowledge and understanding. The Wiley Finance series contains books written specifically for finance and investment professionals as well as sophisticated individual investors and their financial advisors. Book topics range from portfolio management to e- commerce, risk management, financial engineering, valuation and financial instrument analysis, as well as much more. For a list of available titles, please visit our web site at www.WileyFinance.com. Energy and Power Risk Management New Developments in Modeling, Pricing, and Hedging ALEXANDER EYDELAND KRZYSZTOF WOLYNIEC John Wiley & Sons, Inc.
    [Show full text]
  • Course Objectives 1. to Have a Clear Understanding of the Economic Rationale for Risk Management in Energy Sector
    OGET 8006 Energy Trading Markets and Risk L T P C Management Version 1.0 4 0 0 4 Pre-requisites/Exposure Econometrics Modeling, Econometrics Lab Co-requisites Energy Pricing, Oil & Gas Economics Course Objectives 1. To have a clear understanding of the economic rationale for risk management in energy sector. 2. To know the basic techniques for the valuation of forwards, futures, and vanilla options (call and puts); 3. To master the various techniques of hedging practices in terms of energy risk. Course Outcomes On completion of this course, the students will be able to CO1. Understand the concept of various derivative products such as futures, options, and swaps; CO2. To apply hedging models in assessing price risk of various energy derivatives; CO3. To analyse and estimate value at risk for various energy derivatives; CO4. To comprehend various energy derivative products and their performance in Indian and Global Markets; CO5. To integrate the understanding on various energy derivative products and their performance in Indian and Global Markets. Catalog Description Risk is inherent in modern enterprise risk management. Learning different risk management tools such as forwards, futures, options and swaps is necessary. In this course, the focus will be on to learn these tools and the application in Energy price risk management. Students will be applying their econometric skills in learning various risk management models for hedging. Practical application of business data analysis will be done in the class for integrating theories and real business data. Class participation is a fundamental aspect of this course. Students will be encouraged to actively take part in lab activities and to give an oral group presentation.
    [Show full text]
  • Regulation in Energy Derivatives Trading
    University of Colorado Law School Colorado Law Scholarly Commons Articles Colorado Law Faculty Scholarship 2007 Beyond Enron: Regulation in Energy Derivatives Trading Alexia Brunet University of Colorado Law School Meredith Shafe Chapman and Cutler LLP Follow this and additional works at: https://scholar.law.colorado.edu/articles Part of the Energy and Utilities Law Commons, and the Securities Law Commons Citation Information Alexia Brunet and Meredith Shafe, Beyond Enron: Regulation in Energy Derivatives Trading, 27 NW. J. INT'L. L. & BUS. 665 (2007), available at https://scholar.law.colorado.edu/articles/319. Copyright Statement Copyright protected. Use of materials from this collection beyond the exceptions provided for in the Fair Use and Educational Use clauses of the U.S. Copyright Law may violate federal law. Permission to publish or reproduce is required. This Article is brought to you for free and open access by the Colorado Law Faculty Scholarship at Colorado Law Scholarly Commons. It has been accepted for inclusion in Articles by an authorized administrator of Colorado Law Scholarly Commons. For more information, please contact [email protected]. +(,121/,1( Citation: 27 Nw. J. Int'l L. & Bus. 665 2006-2007 Provided by: William A. Wise Law Library Content downloaded/printed from HeinOnline Mon Mar 27 18:34:26 2017 -- Your use of this HeinOnline PDF indicates your acceptance of HeinOnline's Terms and Conditions of the license agreement available at http://heinonline.org/HOL/License -- The search text of this PDF is generated from uncorrected OCR text. -- To obtain permission to use this article beyond the scope of your HeinOnline license, please use: Copyright Information Beyond Enron: Regulation in Energy Derivatives Trading Alexia Brunet* & Meredith Shafe** I.
    [Show full text]
  • Dynamically Hedging Oil and Currency Futures Using Receding Horizontal Control and Stochastic Programming Paul Edward Cottrell Walden University
    Walden University ScholarWorks Walden Dissertations and Doctoral Studies Walden Dissertations and Doctoral Studies Collection 2015 Dynamically Hedging Oil and Currency Futures Using Receding Horizontal Control and Stochastic Programming Paul Edward Cottrell Walden University Follow this and additional works at: https://scholarworks.waldenu.edu/dissertations Part of the Economics Commons, Finance and Financial Management Commons, and the Oil, Gas, and Energy Commons This Dissertation is brought to you for free and open access by the Walden Dissertations and Doctoral Studies Collection at ScholarWorks. It has been accepted for inclusion in Walden Dissertations and Doctoral Studies by an authorized administrator of ScholarWorks. For more information, please contact [email protected]. Walden University College of Management and Technology This is to certify that the doctoral dissertation by Paul Cottrell has been found to be complete and satisfactory in all respects, and that any and all revisions required by the review committee have been made. Review Committee Dr. David Bouvin, Committee Chairperson, Management Faculty Dr. Branford McAllister, Committee Member, Management Faculty Dr. Jeffrey Prinster, University Reviewer, Management Faculty Chief Academic Officer Eric Riedel, Ph.D. Walden University 2015 Abstract Dynamically Hedging Oil and Currency Futures Using Receding Horizontal Control and Stochastic Programming by Paul Edward Cottrell MBA, Wayne State University, 2008 BS, Wayne State University, 2007 Dissertation Submitted in Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy Finance Walden University February 2015 Abstract There is a lack of research in the area of hedging future contracts, especially in illiquid or very volatile market conditions. It is important to understand the volatility of the oil and currency markets because reduced fluctuations in these markets could lead to better hedging performance.
    [Show full text]
  • ©Copyright 2016 Thomas Fillebeen How Do Small Players Deduce Beliefs About Uncertainty? a Look at Texas Shale Oil Investments
    ©Copyright 2016 Thomas Fillebeen How Do Small Players Deduce Beliefs about Uncertainty? A Look at Texas Shale Oil Investments Thomas Fillebeen A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy University of Washington 2016 Reading Committee: Chris Anderson, Chair Robert Halvorsen, Chair Eric Zivot Program Authorized to Offer Degree: Economics University of Washington Abstract How Do Small Players Deduce Beliefs about Uncertainty? A Look at Texas Shale Oil Investments Thomas Fillebeen Co-Chairs of the Supervisory Committee: Associate Professor Chris Anderson School of Aquatic and Fishery Sciences Professor Robert Halvorsen Department of Economics Derivative markets enable firms to eliminate unwanted risk and, thereby, focus on their core competence. We ask whether small firms respond to changes in complex risk struc- tures, using the emerging Texas shale oil industry. Unlike their conventional drilling coun- terparts, shale oil producers are small, with short production lead times and most revenue earned in two to three years. This exposes them to recent unprecedented volatility in product prices, production costs, and-in the Permian, pipeline transportation basis risk. We develop a real option model of their decision process, within which we measure firm responsiveness to volatility. To estimate revenue expectations, we use forward-looking time-varying beliefs deduced from futures and futures option prices. For costs, we use expectations about the evolution of production technology and forward-contracted trans- port capacity. Our results show that investment in new wells responds optimally not only to time-varying market price, but also to a second source of uncertainty: transportation basis.
    [Show full text]