Geometry and Symmetry, Problem Set #4 Summer 2010 Relating
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Analytic Geometry
Guide Study Georgia End-Of-Course Tests Georgia ANALYTIC GEOMETRY TABLE OF CONTENTS INTRODUCTION ...........................................................................................................5 HOW TO USE THE STUDY GUIDE ................................................................................6 OVERVIEW OF THE EOCT .........................................................................................8 PREPARING FOR THE EOCT ......................................................................................9 Study Skills ........................................................................................................9 Time Management .....................................................................................10 Organization ...............................................................................................10 Active Participation ...................................................................................11 Test-Taking Strategies .....................................................................................11 Suggested Strategies to Prepare for the EOCT ..........................................12 Suggested Strategies the Day before the EOCT ........................................13 Suggested Strategies the Morning of the EOCT ........................................13 Top 10 Suggested Strategies during the EOCT .........................................14 TEST CONTENT ........................................................................................................15 -

Chapter 11. Three Dimensional Analytic Geometry and Vectors
Chapter 11. Three dimensional analytic geometry and vectors. Section 11.5 Quadric surfaces. Curves in R2 : x2 y2 ellipse + =1 a2 b2 x2 y2 hyperbola − =1 a2 b2 parabola y = ax2 or x = by2 A quadric surface is the graph of a second degree equation in three variables. The most general such equation is Ax2 + By2 + Cz2 + Dxy + Exz + F yz + Gx + Hy + Iz + J =0, where A, B, C, ..., J are constants. By translation and rotation the equation can be brought into one of two standard forms Ax2 + By2 + Cz2 + J =0 or Ax2 + By2 + Iz =0 In order to sketch the graph of a quadric surface, it is useful to determine the curves of intersection of the surface with planes parallel to the coordinate planes. These curves are called traces of the surface. Ellipsoids The quadric surface with equation x2 y2 z2 + + =1 a2 b2 c2 is called an ellipsoid because all of its traces are ellipses. 2 1 x y 3 2 1 z ±1 ±2 ±3 ±1 ±2 The six intercepts of the ellipsoid are (±a, 0, 0), (0, ±b, 0), and (0, 0, ±c) and the ellipsoid lies in the box |x| ≤ a, |y| ≤ b, |z| ≤ c Since the ellipsoid involves only even powers of x, y, and z, the ellipsoid is symmetric with respect to each coordinate plane. Example 1. Find the traces of the surface 4x2 +9y2 + 36z2 = 36 1 in the planes x = k, y = k, and z = k. Identify the surface and sketch it. Hyperboloids Hyperboloid of one sheet. The quadric surface with equations x2 y2 z2 1. -

ANALYTIC GEOMETRY Revision Log
Guide Study Georgia End-Of-Course Tests Georgia ANALYTIC GEOMETRYJanuary 2014 Revision Log August 2013: Unit 7 (Applications of Probability) page 200; Key Idea #7 – text and equation were updated to denote intersection rather than union page 203; Review Example #2 Solution – union symbol has been corrected to intersection symbol in lines 3 and 4 of the solution text January 2014: Unit 1 (Similarity, Congruence, and Proofs) page 33; Review Example #2 – “Segment Addition Property” has been updated to “Segment Addition Postulate” in step 13 of the solution page 46; Practice Item #2 – text has been specified to indicate that point V lies on segment SU page 59; Practice Item #1 – art has been updated to show points on YX and YZ Unit 3 (Circles and Volume) page 74; Key Idea #17 – the reference to Key Idea #15 has been updated to Key Idea #16 page 84; Key Idea #3 – the degree symbol (°) has been removed from 360, and central angle is noted by θ instead of x in the formula and the graphic page 84; Important Tip – the word “formulas” has been corrected to “formula”, and x has been replaced by θ in the formula for arc length page 85; Key Idea #4 – the degree symbol (°) has been added to the conversion factor page 85; Key Idea #5 – text has been specified to indicate a central angle, and central angle is noted by θ instead of x page 85; Key Idea #6 – the degree symbol (°) has been removed from 360, and central angle is noted by θ instead of x in the formula and the graphic page 87; Solution Step i – the degree symbol (°) has been added to the conversion -

Analytic Geometry
STATISTIC ANALYTIC GEOMETRY SESSION 3 STATISTIC SESSION 3 Session 3 Analytic Geometry Geometry is all about shapes and their properties. If you like playing with objects, or like drawing, then geometry is for you! Geometry can be divided into: Plane Geometry is about flat shapes like lines, circles and triangles ... shapes that can be drawn on a piece of paper Solid Geometry is about three dimensional objects like cubes, prisms, cylinders and spheres Point, Line, Plane and Solid A Point has no dimensions, only position A Line is one-dimensional A Plane is two dimensional (2D) A Solid is three-dimensional (3D) Plane Geometry Plane Geometry is all about shapes on a flat surface (like on an endless piece of paper). 2D Shapes Activity: Sorting Shapes Triangles Right Angled Triangles Interactive Triangles Quadrilaterals (Rhombus, Parallelogram, etc) Rectangle, Rhombus, Square, Parallelogram, Trapezoid and Kite Interactive Quadrilaterals Shapes Freeplay Perimeter Area Area of Plane Shapes Area Calculation Tool Area of Polygon by Drawing Activity: Garden Area General Drawing Tool Polygons A Polygon is a 2-dimensional shape made of straight lines. Triangles and Rectangles are polygons. Here are some more: Pentagon Pentagra m Hexagon Properties of Regular Polygons Diagonals of Polygons Interactive Polygons The Circle Circle Pi Circle Sector and Segment Circle Area by Sectors Annulus Activity: Dropping a Coin onto a Grid Circle Theorems (Advanced Topic) Symbols There are many special symbols used in Geometry. Here is a short reference for you: -

Can One Design a Geometry Engine? on the (Un) Decidability of Affine
Noname manuscript No. (will be inserted by the editor) Can one design a geometry engine? On the (un)decidability of certain affine Euclidean geometries Johann A. Makowsky Received: June 4, 2018/ Accepted: date Abstract We survey the status of decidabilty of the consequence relation in various ax- iomatizations of Euclidean geometry. We draw attention to a widely overlooked result by Martin Ziegler from 1980, which proves Tarski’s conjecture on the undecidability of finitely axiomatizable theories of fields. We elaborate on how to use Ziegler’s theorem to show that the consequence relations for the first order theory of the Hilbert plane and the Euclidean plane are undecidable. As new results we add: (A) The first order consequence relations for Wu’s orthogonal and metric geometries (Wen- Ts¨un Wu, 1984), and for the axiomatization of Origami geometry (J. Justin 1986, H. Huzita 1991) are undecidable. It was already known that the universal theory of Hilbert planes and Wu’s orthogonal geom- etry is decidable. We show here using elementary model theoretic tools that (B) the universal first order consequences of any geometric theory T of Pappian planes which is consistent with the analytic geometry of the reals is decidable. The techniques used were all known to experts in mathematical logic and geometry in the past but no detailed proofs are easily accessible for practitioners of symbolic computation or automated theorem proving. Keywords Euclidean Geometry · Automated Theorem Proving · Undecidability arXiv:1712.07474v3 [cs.SC] 1 Jun 2018 J.A. Makowsky Faculty of Computer Science, Technion–Israel Institute of Technology, Haifa, Israel E-mail: [email protected] 2 J.A. -

Finite Projective Geometries 243
FINITE PROJECTÎVEGEOMETRIES* BY OSWALD VEBLEN and W. H. BUSSEY By means of such a generalized conception of geometry as is inevitably suggested by the recent and wide-spread researches in the foundations of that science, there is given in § 1 a definition of a class of tactical configurations which includes many well known configurations as well as many new ones. In § 2 there is developed a method for the construction of these configurations which is proved to furnish all configurations that satisfy the definition. In §§ 4-8 the configurations are shown to have a geometrical theory identical in most of its general theorems with ordinary projective geometry and thus to afford a treatment of finite linear group theory analogous to the ordinary theory of collineations. In § 9 reference is made to other definitions of some of the configurations included in the class defined in § 1. § 1. Synthetic definition. By a finite projective geometry is meant a set of elements which, for sugges- tiveness, are called points, subject to the following five conditions : I. The set contains a finite number ( > 2 ) of points. It contains subsets called lines, each of which contains at least three points. II. If A and B are distinct points, there is one and only one line that contains A and B. HI. If A, B, C are non-collinear points and if a line I contains a point D of the line AB and a point E of the line BC, but does not contain A, B, or C, then the line I contains a point F of the line CA (Fig. -

Topics in Complex Analytic Geometry
version: February 24, 2012 (revised and corrected) Topics in Complex Analytic Geometry by Janusz Adamus Lecture Notes PART II Department of Mathematics The University of Western Ontario c Copyright by Janusz Adamus (2007-2012) 2 Janusz Adamus Contents 1 Analytic tensor product and fibre product of analytic spaces 5 2 Rank and fibre dimension of analytic mappings 8 3 Vertical components and effective openness criterion 17 4 Flatness in complex analytic geometry 24 5 Auslander-type effective flatness criterion 31 This document was typeset using AMS-LATEX. Topics in Complex Analytic Geometry - Math 9607/9608 3 References [I] J. Adamus, Complex analytic geometry, Lecture notes Part I (2008). [A1] J. Adamus, Natural bound in Kwieci´nski'scriterion for flatness, Proc. Amer. Math. Soc. 130, No.11 (2002), 3165{3170. [A2] J. Adamus, Vertical components in fibre powers of analytic spaces, J. Algebra 272 (2004), no. 1, 394{403. [A3] J. Adamus, Vertical components and flatness of Nash mappings, J. Pure Appl. Algebra 193 (2004), 1{9. [A4] J. Adamus, Flatness testing and torsion freeness of analytic tensor powers, J. Algebra 289 (2005), no. 1, 148{160. [ABM1] J. Adamus, E. Bierstone, P. D. Milman, Uniform linear bound in Chevalley's lemma, Canad. J. Math. 60 (2008), no.4, 721{733. [ABM2] J. Adamus, E. Bierstone, P. D. Milman, Geometric Auslander criterion for flatness, to appear in Amer. J. Math. [ABM3] J. Adamus, E. Bierstone, P. D. Milman, Geometric Auslander criterion for openness of an algebraic morphism, preprint (arXiv:1006.1872v1). [Au] M. Auslander, Modules over unramified regular local rings, Illinois J. -

Geometry: Euclid and Beyond, by Robin Hartshorne, Springer-Verlag, New York, 2000, Xi+526 Pp., $49.95, ISBN 0-387-98650-2
BULLETIN (New Series) OF THE AMERICAN MATHEMATICAL SOCIETY Volume 39, Number 4, Pages 563{571 S 0273-0979(02)00949-7 Article electronically published on July 9, 2002 Geometry: Euclid and beyond, by Robin Hartshorne, Springer-Verlag, New York, 2000, xi+526 pp., $49.95, ISBN 0-387-98650-2 1. Introduction The first geometers were men and women who reflected on their experiences while doing such activities as building small shelters and bridges, making pots, weaving cloth, building altars, designing decorations, or gazing into the heavens for portentous signs or navigational aides. Main aspects of geometry emerged from three strands of early human activity that seem to have occurred in most cultures: art/patterns, navigation/stargazing, and building structures. These strands developed more or less independently into varying studies and practices that eventually were woven into what we now call geometry. Art/Patterns: To produce decorations for their weaving, pottery, and other objects, early artists experimented with symmetries and repeating patterns. Later the study of symmetries of patterns led to tilings, group theory, crystallography, finite geometries, and in modern times to security codes and digital picture com- pactifications. Early artists also explored various methods of representing existing objects and living things. These explorations led to the study of perspective and then projective geometry and descriptive geometry, and (in the 20th century) to computer-aided graphics, the study of computer vision in robotics, and computer- generated movies (for example, Toy Story ). Navigation/Stargazing: For astrological, religious, agricultural, and other purposes, ancient humans attempted to understand the movement of heavenly bod- ies (stars, planets, Sun, and Moon) in the apparently hemispherical sky. -

Chapter 1: Analytic Geometry
1 Analytic Geometry Much of the mathematics in this chapter will be review for you. However, the examples will be oriented toward applications and so will take some thought. In the (x,y) coordinate system we normally write the x-axis horizontally, with positive numbers to the right of the origin, and the y-axis vertically, with positive numbers above the origin. That is, unless stated otherwise, we take “rightward” to be the positive x- direction and “upward” to be the positive y-direction. In a purely mathematical situation, we normally choose the same scale for the x- and y-axes. For example, the line joining the origin to the point (a,a) makes an angle of 45◦ with the x-axis (and also with the y-axis). In applications, often letters other than x and y are used, and often different scales are chosen in the horizontal and vertical directions. For example, suppose you drop something from a window, and you want to study how its height above the ground changes from second to second. It is natural to let the letter t denote the time (the number of seconds since the object was released) and to let the letter h denote the height. For each t (say, at one-second intervals) you have a corresponding height h. This information can be tabulated, and then plotted on the (t, h) coordinate plane, as shown in figure 1.0.1. We use the word “quadrant” for each of the four regions into which the plane is divided by the axes: the first quadrant is where points have both coordinates positive, or the “northeast” portion of the plot, and the second, third, and fourth quadrants are counted off counterclockwise, so the second quadrant is the northwest, the third is the southwest, and the fourth is the southeast. -

Analytic Geometry
INTRODUCTION TO ANALYTIC GEOMETRY BY PEECEY R SMITH, PH.D. N PROFESSOR OF MATHEMATICS IN THE SHEFFIELD SCIENTIFIC SCHOOL YALE UNIVERSITY AND AKTHUB SULLIVAN GALE, PH.D. ASSISTANT PROFESSOR OF MATHEMATICS IN THE UNIVERSITY OF ROCHESTER GINN & COMPANY BOSTON NEW YORK CHICAGO LONDON COPYRIGHT, 1904, 1905, BY ARTHUR SULLIVAN GALE ALL BIGHTS RESERVED 65.8 GINN & COMPANY PRO- PRIETORS BOSTON U.S.A. PEE FACE In preparing this volume the authors have endeavored to write a drill book for beginners which presents, in a manner conform- ing with modern ideas, the fundamental concepts of the subject. The subject-matter is slightly more than the minimum required for the calculus, but only as much more as is necessary to permit of some choice on the part of the teacher. It is believed that the text is complete for students finishing their study of mathematics with a course in Analytic Geometry. The authors have intentionally avoided giving the book the form of a treatise on conic sections. Conic sections naturally appear, but chiefly as illustrative of general analytic methods. Attention is called to the method of treatment. The subject is developed after the Euclidean method of definition and theorem, without, however, adhering to formal presentation. The advan- tage is obvious, for the student is made sure of the exact nature of each acquisition. Again, each method is summarized in a rule stated in consecutive steps. This is a gain in clearness. Many illustrative examples are worked out in the text. Emphasis has everywhere been put upon the analytic side, that is, the student is taught to start from the equation. -

Relativistic Spacetime Structure
Relativistic Spacetime Structure Samuel C. Fletcher∗ Department of Philosophy University of Minnesota, Twin Cities & Munich Center for Mathematical Philosophy Ludwig Maximilian University of Munich August 12, 2019 Abstract I survey from a modern perspective what spacetime structure there is according to the general theory of relativity, and what of it determines what else. I describe in some detail both the “standard” and various alternative answers to these questions. Besides bringing many underexplored topics to the attention of philosophers of physics and of science, metaphysicians of science, and foundationally minded physicists, I also aim to cast other, more familiar ones in a new light. 1 Introduction and Scope In the broadest sense, spacetime structure consists in the totality of relations between events and processes described in a spacetime theory, including distance, duration, motion, and (more gener- ally) change. A spacetime theory can attribute more or less such structure, and some parts of that structure may determine other parts. The nature of these structures and their relations of determi- nation bear on the interpretation of the theory—what the world would be like if the theory were true (North, 2009). For example, the structures of spacetime might be taken as its ontological or conceptual posits, and the determination relations might indicate which of these structures is more fundamental (North, 2018). Different perspectives on these questions might also reveal structural similarities with other spacetime theories, providing the resources to articulate how the picture of the world that that theory provides is different (if at all) from what came before, and might be different from what is yet to come.1 ∗Juliusz Doboszewski, Laurenz Hudetz, Eleanor Knox, J. -
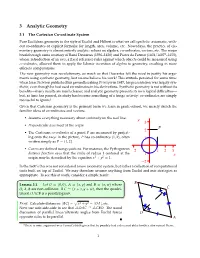
3 Analytic Geometry
3 Analytic Geometry 3.1 The Cartesian Co-ordinate System Pure Euclidean geometry in the style of Euclid and Hilbert is what we call synthetic: axiomatic, with- out co-ordinates or explicit formulæ for length, area, volume, etc. Nowadays, the practice of ele- mentary geometry is almost entirely analytic: reliant on algebra, co-ordinates, vectors, etc. The major breakthrough came courtesy of Rene´ Descartes (1596–1650) and Pierre de Fermat (1601/16071–1655), whose introduction of an axis, a fixed reference ruler against which objects could be measured using co-ordinates, allowed them to apply the Islamic invention of algebra to geometry, resulting in more efficient computations. The new geometry was revolutionary, so much so that Descartes felt the need to justify his argu- ments using synthetic geometry, lest no-one believe his work! This attitude persisted for some time: when Issac Newton published his groundbreaking Principia in 1687, his presentation was largely syn- thetic, even though he had used co-ordinates in his derivations. Synthetic geometry is not without its benefits—many results are much cleaner, and analytic geometry presents its own logical difficulties— but, as time has passed, its study has become something of a fringe activity: co-ordinates are simply too useful to ignore! Given that Cartesian geometry is the primary form we learn in grade-school, we merely sketch the familiar ideas of co-ordinates and vectors. • Assume everything necessary about on the real line. continuity y 3 • Perpendicular axes meet at the origin. P 2 • The Cartesian co-ordinates of a point P are measured by project- ing onto the axes: in the picture, P has co-ordinates (1, 2), often 1 written simply as P = (1, 2).