Astrophysics on the Orbits of the Outer Satellites of Jupiter
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Satellite Situation Report
NASA Office of Public Affairs Satellite Situation Report VOLUME 17 NUMBER 6 DECEMBER 31, 1977 (NASA-TM-793t5) SATELLITE SITUATION~ BEPORT, N8-17131 VOLUME 17, NO. 6 (NASA) 114 F HC A06/mF A01 CSCL 05B Unclas G3/15 05059 Goddard Space Flight Center Greenbelt, Maryland NOTICE .THIS DOCUMENT HAS'BEEN REPRODUCED FROM THE BEST COPY FURNISHED US BY THE SPONSORING AGENCY. ALTHOUGH IT IS RECOGNIZED THAT CERTAIN PORTIONS' ARE ILLEGIBLE, IT IS BEING RELEASED IN THE INTEREST OF MAKING AVAILABLE AS MUCH INFORMATION AS POSSIBLE. OFFICE OF PUBLIC AFFAIRS GCDDARD SPACE FLIGHT CENTER NATIONAL AERONAUTICS AND SPACE ADMINISTRATION VOLUME 17 NO. 6 DECEMBER 31, 1977 SATELLITE SITUATION REPORT THIS REPORT IS PUBLIShED AND DISTRIBUTED BY THE OFFICE OF PUBLIC AFFAIRS, GSFC. GODPH DRgP2 FE I T ERETAO5MUJS E SMITHSONIAN ASTRCPHYSICAL OBSERVATORY. SPACEFLIGHT TRACKING AND DATA NETWORK. NOTE: The Satellite Situation Report dated October 31, 1977, contained an entry in the "Objects Decayed Within the Reporting Period" that 1977 042P, object number 10349, decayed on September 21, 1977. That entry was in error. The object is still in orbit. SPACE OBJECTS BOX SCORE OBJECTS IN ORBIT DECAYED OBJECTS AUSTRALIA I I CANACA 8 0 ESA 4 0 ESRO 1 9 FRANCE 54 26 FRANCE/FRG 2 0 FRG 9 3 INCIA 1 0 INDONESIA 2 0 INTERNATIONAL TELECOM- MUNICATIONS SATELLITE ORGANIZATION (ITSO) 22 0 ITALY 1 4 JAPAN 27 0 NATC 4 0 NETHERLANDS 0 4 PRC 6 14 SPAIN 1 0 UK 11 4 US 2928 1523 USSR 1439 4456 TOTAL 4E21 6044 INTER- CBJECTS IN ORIT NATIONAL CATALOG PERIOD INCLI- APOGEE PERIGEE TQANSMITTTNG DESIGNATION NAME NUMBER SOURCE LAUNCH MINUTES NATION KM. -

Constructing the Secular Architecture of the Solar System I: the Giant Planets
Astronomy & Astrophysics manuscript no. secular c ESO 2018 May 29, 2018 Constructing the secular architecture of the solar system I: The giant planets A. Morbidelli1, R. Brasser1, K. Tsiganis2, R. Gomes3, and H. F. Levison4 1 Dep. Cassiopee, University of Nice - Sophia Antipolis, CNRS, Observatoire de la Cˆote d’Azur; Nice, France 2 Department of Physics, Aristotle University of Thessaloniki; Thessaloniki, Greece 3 Observat´orio Nacional; Rio de Janeiro, RJ, Brasil 4 Southwest Research Institute; Boulder, CO, USA submitted: 13 July 2009; accepted: 31 August 2009 ABSTRACT Using numerical simulations, we show that smooth migration of the giant planets through a planetesimal disk leads to an orbital architecture that is inconsistent with the current one: the resulting eccentricities and inclinations of their orbits are too small. The crossing of mutual mean motion resonances by the planets would excite their orbital eccentricities but not their orbital inclinations. Moreover, the amplitudes of the eigenmodes characterising the current secular evolution of the eccentricities of Jupiter and Saturn would not be reproduced correctly; only one eigenmode is excited by resonance-crossing. We show that, at the very least, encounters between Saturn and one of the ice giants (Uranus or Neptune) need to have occurred, in order to reproduce the current secular properties of the giant planets, in particular the amplitude of the two strongest eigenmodes in the eccentricities of Jupiter and Saturn. Key words. Solar System: formation 1. Introduction Snellgrove (2001). The top panel shows the evolution of the semi major axes, where Saturn’ semi-major axis is depicted The formation and evolution of the solar system is a longstand- by the upper curve and that of Jupiter is the lower trajectory. -

Astrometric Positions for 18 Irregular Satellites of Giant Planets from 23
Astronomy & Astrophysics manuscript no. Irregulares c ESO 2018 October 20, 2018 Astrometric positions for 18 irregular satellites of giant planets from 23 years of observations,⋆,⋆⋆,⋆⋆⋆,⋆⋆⋆⋆ A. R. Gomes-Júnior1, M. Assafin1,†, R. Vieira-Martins1, 2, 3,‡, J.-E. Arlot4, J. I. B. Camargo2, 3, F. Braga-Ribas2, 5,D.N. da Silva Neto6, A. H. Andrei1, 2,§, A. Dias-Oliveira2, B. E. Morgado1, G. Benedetti-Rossi2, Y. Duchemin4, 7, J. Desmars4, V. Lainey4, W. Thuillot4 1 Observatório do Valongo/UFRJ, Ladeira Pedro Antônio 43, CEP 20.080-090 Rio de Janeiro - RJ, Brazil e-mail: [email protected] 2 Observatório Nacional/MCT, R. General José Cristino 77, CEP 20921-400 Rio de Janeiro - RJ, Brazil e-mail: [email protected] 3 Laboratório Interinstitucional de e-Astronomia - LIneA, Rua Gal. José Cristino 77, Rio de Janeiro, RJ 20921-400, Brazil 4 Institut de mécanique céleste et de calcul des éphémérides - Observatoire de Paris, UMR 8028 du CNRS, 77 Av. Denfert-Rochereau, 75014 Paris, France e-mail: [email protected] 5 Federal University of Technology - Paraná (UTFPR / DAFIS), Rua Sete de Setembro, 3165, CEP 80230-901, Curitiba, PR, Brazil 6 Centro Universitário Estadual da Zona Oeste, Av. Manual Caldeira de Alvarenga 1203, CEP 23.070-200 Rio de Janeiro RJ, Brazil 7 ESIGELEC-IRSEEM, Technopôle du Madrillet, Avenue Galilée, 76801 Saint-Etienne du Rouvray, France Received: Abr 08, 2015; accepted: May 06, 2015 ABSTRACT Context. The irregular satellites of the giant planets are believed to have been captured during the evolution of the solar system. Knowing their physical parameters, such as size, density, and albedo is important for constraining where they came from and how they were captured. -

The Effect of Jupiter\'S Mass Growth on Satellite Capture
A&A 414, 727–734 (2004) Astronomy DOI: 10.1051/0004-6361:20031645 & c ESO 2004 Astrophysics The effect of Jupiter’s mass growth on satellite capture Retrograde case E. Vieira Neto1;?,O.C.Winter1, and T. Yokoyama2 1 Grupo de Dinˆamica Orbital & Planetologia, UNESP, CP 205 CEP 12.516-410 Guaratinguet´a, SP, Brazil e-mail: [email protected] 2 Universidade Estadual Paulista, IGCE, DEMAC, CP 178 CEP 13.500-970 Rio Claro, SP, Brazil e-mail: [email protected] Received 13 June 2003 / Accepted 12 September 2003 Abstract. Gravitational capture can be used to explain the existence of the irregular satellites of giants planets. However, it is only the first step since the gravitational capture is temporary. Therefore, some kind of non-conservative effect is necessary to to turn the temporary capture into a permanent one. In the present work we study the effects of Jupiter mass growth for the permanent capture of retrograde satellites. An analysis of the zero velocity curves at the Lagrangian point L1 indicates that mass accretion provides an increase of the confinement region (delimited by the zero velocity curve, where particles cannot escape from the planet) favoring permanent captures. Adopting the restricted three-body problem, Sun-Jupiter-Particle, we performed numerical simulations backward in time considering the decrease of M . We considered initial conditions of the particles to be retrograde, at pericenter, in the region 100 R a 400 R and 0 e 0:5. The results give Jupiter’s mass at the X moment when the particle escapes from the planet. -

The Convention Ear 58 (Y)Ears of Telling It Like It Isn’T!
The Convention Ear 58 (Y)Ears of Telling It Like It Isn’t! Wednesday, July 25, 2018 Volume LIX, Issue III 25 Hour Convention Coverage Astronomers, Classicists Scramble to Invent Twelve More Stories About Zeus in Order to Name New Moons of Jupiter That’s Entertainment! Results With the recent discovery of twelve new moons around Jupiter, astronomers Congratulations to the following dele- and classicists have put aside their differences (they’ve agreed to spell it gates who have been selected to per- “Jupiter” not “Iuppiter”) to take on the challenge of naming the celestial bod- ies. As is tradition, the new moons will be named after various loves the king form in That's Entertainment! of the gods was said to have had; the only problem is, after 53 moons, we’ve Soren Adams (KY) run out of names. Madelyn Bedard & Ruth Weaver (MA) “This is a different kind of nomenclature problem than what we’re used to,” Cameron Crowley (TX) said astronomer Dr. Joey Chatelain, who looks at the sky for a living. “We’ve Sophia Dort (VA) already used Metis, Adrastea, Amalthea, Thebe, Io, Europa, Ganymede, Cal- Jeffrey Frenkel-Popell (CA) listo,” <we left at this point, did laundry, got lunch, then came back - the list Keon Honaryar (CA) was still going> “... Sinope, Sponde, Autonoe, Megaclite, and S/2003 J 2. We Kiana Hu (CA) simply don’t have any more names to use.” Illinois Dance Troupe (IL) To solve this problem, astronomers have turned to classicists for help. “The Owen Lockwood (OH) answer is simple,” said one leading Classics professor, who wished to remain Akhila Nataraj (FL) anonymous. -

Orbital Debris: a Chronology
NASA/TP-1999-208856 January 1999 Orbital Debris: A Chronology David S. F. Portree Houston, Texas Joseph P. Loftus, Jr Lwldon B. Johnson Space Center Houston, Texas David S. F. Portree is a freelance writer working in Houston_ Texas Contents List of Figures ................................................................................................................ iv Preface ........................................................................................................................... v Acknowledgments ......................................................................................................... vii Acronyms and Abbreviations ........................................................................................ ix The Chronology ............................................................................................................. 1 1961 ......................................................................................................................... 4 1962 ......................................................................................................................... 5 963 ......................................................................................................................... 5 964 ......................................................................................................................... 6 965 ......................................................................................................................... 6 966 ........................................................................................................................ -

Ice& Stone 2020
Ice & Stone 2020 WEEK 33: AUGUST 9-15 Presented by The Earthrise Institute # 33 Authored by Alan Hale About Ice And Stone 2020 It is my pleasure to welcome all educators, students, topics include: main-belt asteroids, near-Earth asteroids, and anybody else who might be interested, to Ice and “Great Comets,” spacecraft visits (both past and Stone 2020. This is an educational package I have put future), meteorites, and “small bodies” in popular together to cover the so-called “small bodies” of the literature and music. solar system, which in general means asteroids and comets, although this also includes the small moons of Throughout 2020 there will be various comets that are the various planets as well as meteors, meteorites, and visible in our skies and various asteroids passing by Earth interplanetary dust. Although these objects may be -- some of which are already known, some of which “small” compared to the planets of our solar system, will be discovered “in the act” -- and there will also be they are nevertheless of high interest and importance various asteroids of the main asteroid belt that are visible for several reasons, including: as well as “occultations” of stars by various asteroids visible from certain locations on Earth’s surface. Ice a) they are believed to be the “leftovers” from the and Stone 2020 will make note of these occasions and formation of the solar system, so studying them provides appearances as they take place. The “Comet Resource valuable insights into our origins, including Earth and of Center” at the Earthrise web site contains information life on Earth, including ourselves; about the brighter comets that are visible in the sky at any given time and, for those who are interested, I will b) we have learned that this process isn’t over yet, and also occasionally share information about the goings-on that there are still objects out there that can impact in my life as I observe these comets. -

The Rae Table of Earth Satellites 1957-1986 the Rae Table Ofearth Satellites
THE RAE TABLE OF EARTH SATELLITES 1957-1986 THE RAE TABLE OFEARTH SATELLITES 1957-1986 compiled at The Royal Aircraft Establishment, Famborough, Hants, England by D.G. King-Dele, FRS, D.M.C. Walker, PhD, J.A. Pilkington, BSc, A.N. Winterbottom, H. Hiller, BSc and G.E. Perry, MBE The Table is a chronological list of the 2869 launches of satellites and space vehicles between 1957 and the end of 1986, giving the name and international designation of each satellite and its associated rocket(s), with the date of launch, lifetime (actual or estimated), mass, shape, dimensions and at least one set of orbital parameters. Other fragments associated with a launch, and space vehicles that escape from the Earth's influence, are given without details. Including fragments, more than 17000 satellites appear in the 893 pages of the tabulation, and there is a full Index. M TOCKTON S P R E S S © Crown copyright 1981, 1983, 1987 Softcover reprint of the hardcover 3rd edition 1987 978-0-333-39275-1 Published by permission of the Controller of Her Majesty's Stationery Office. All rights reserved. No part of this publication may be reproduced, or transmitted, in any form or by any means, without permission. Published in the United States and Canada by STOCKTON PRESS, 1987 15 East 26th Street, New York, N.Y. 10010 Library of Congress Cataloging-in-Publication Data The R.A.E. table of earth satellites, 1957-1986. Rev. ed. of: The RAE table of earth satellites, 1957- 1980. 2nd ed. 1981. 1. Artificial satellites- Registers. -
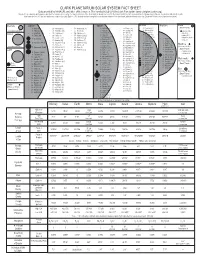
CLARK PLANETARIUM SOLAR SYSTEM FACT SHEET Data Provided by NASA/JPL and Other Official Sources
CLARK PLANETARIUM SOLAR SYSTEM FACT SHEET Data provided by NASA/JPL and other official sources. This handout ©July 2013 by Clark Planetarium (www.clarkplanetarium.org). May be freely copied by professional educators for classroom use only. The known satellites of the Solar System shown here next to their planets with their sizes (mean diameter in km) in parenthesis. The planets and satellites (with diameters above 1,000 km) are depicted in relative size (with Earth = 0.500 inches) and are arranged in order by their distance from the planet, with the closest at the top. Distances from moon to planet are not listed. Mercury Jupiter Saturn Uranus Neptune Pluto • 1- Metis (44) • 26- Hermippe (4) • 54- Hegemone (3) • 1- S/2009 S1 (1) • 33- Erriapo (10) • 1- Cordelia (40.2) (Dwarf Planet) (no natural satellites) • 2- Adrastea (16) • 27- Praxidike (6.8) • 55- Aoede (4) • 2- Pan (26) • 34- Siarnaq (40) • 2- Ophelia (42.8) • Charon (1186) • 3- Bianca (51.4) Venus • 3- Amalthea (168) • 28- Thelxinoe (2) • 56- Kallichore (2) • 3- Daphnis (7) • 35- Skoll (6) • Nix (60?) • 4- Thebe (98) • 29- Helike (4) • 57- S/2003 J 23 (2) • 4- Atlas (32) • 36- Tarvos (15) • 4- Cressida (79.6) • Hydra (50?) • 5- Desdemona (64) • 30- Iocaste (5.2) • 58- S/2003 J 5 (4) • 5- Prometheus (100.2) • 37- Tarqeq (7) • Kerberos (13-34?) • 5- Io (3,643.2) • 6- Pandora (83.8) • 38- Greip (6) • 6- Juliet (93.6) • 1- Naiad (58) • 31- Ananke (28) • 59- Callirrhoe (7) • Styx (??) • 7- Epimetheus (119) • 39- Hyrrokkin (8) • 7- Portia (135.2) • 2- Thalassa (80) • 6- Europa (3,121.6) -

Orbital Resonances and Chaos in the Solar System
Solar system Formation and Evolution ASP Conference Series, Vol. 149, 1998 D. Lazzaro et al., eds. ORBITAL RESONANCES AND CHAOS IN THE SOLAR SYSTEM Renu Malhotra Lunar and Planetary Institute 3600 Bay Area Blvd, Houston, TX 77058, USA E-mail: [email protected] Abstract. Long term solar system dynamics is a tale of orbital resonance phe- nomena. Orbital resonances can be the source of both instability and long term stability. This lecture provides an overview, with simple models that elucidate our understanding of orbital resonance phenomena. 1. INTRODUCTION The phenomenon of resonance is a familiar one to everybody from childhood. A very young child is delighted in a playground swing when an older companion drives the swing at its natural frequency and rapidly increases the swing amplitude; the older child accomplishes the same on her own without outside assistance by driving the swing at a frequency twice that of its natural frequency. Resonance phenomena in the Solar system are essentially similar – the driving of a dynamical system by a periodic force at a frequency which is a rational multiple of the natural frequency. In fact, there are many mathematical similarities with the playground analogy, including the fact of nonlinearity of the oscillations, which plays a fundamental role in the long term evolution of orbits in the planetary system. But there is also an important difference: in the playground, the child adjusts her driving frequency to remain in tune – hence in resonance – with the natural frequency which changes with the amplitude of the swing. Such self-tuning is sometimes realized in the Solar system; but it is more often and more generally the case that resonances come-and-go. -

Three-Body Capture of Irregular Satellites: Application to Jupiter
Icarus 208 (2010) 824–836 Contents lists available at ScienceDirect Icarus journal homepage: www.elsevier.com/locate/icarus Three-body capture of irregular satellites: Application to Jupiter Catherine M. Philpott a,*, Douglas P. Hamilton a, Craig B. Agnor b a Department of Astronomy, University of Maryland, College Park, MD 20742-2421, USA b Astronomy Unit, School of Mathematical Sciences, Queen Mary University of London, London E14NS, UK article info abstract Article history: We investigate a new theory of the origin of the irregular satellites of the giant planets: capture of one Received 19 October 2009 member of a 100-km binary asteroid after tidal disruption. The energy loss from disruption is sufficient Revised 24 March 2010 for capture, but it cannot deliver the bodies directly to the observed orbits of the irregular satellites. Accepted 26 March 2010 Instead, the long-lived capture orbits subsequently evolve inward due to interactions with a tenuous cir- Available online 7 April 2010 cumplanetary gas disk. We focus on the capture by Jupiter, which, due to its large mass, provides a stringent test of our model. Keywords: We investigate the possible fates of disrupted bodies, the differences between prograde and retrograde Irregular satellites captures, and the effects of Callisto on captured objects. We make an impulse approximation and discuss Jupiter, Satellites Planetary dynamics how it allows us to generalize capture results from equal-mass binaries to binaries with arbitrary mass Satellites, Dynamics ratios. Jupiter We find that at Jupiter, binaries offer an increase of a factor of 10 in the capture rate of 100-km objects as compared to single bodies, for objects separated by tens of radii that approach the planet on relatively low-energy trajectories. -

Basic Notations
Appendix A Basic Notations In this Appendix, the basic notations for the mathematical operators and astronom- ical and physical quantities used throughout the book are given. Note that only the most frequently used quantities are mentioned; besides, overlapping symbol definitions and deviations from the basically adopted notations are possible, when appropriate. Mathematical Quantities and Operators kxk is the length (norm) of vector x x y is the scalar product of vectors x and y rr is the gradient operator in the direction of vector r f f ; gg is the Poisson bracket of functions f and g K.m/ or K.k/ (where m D k2) is the complete elliptic integral of the first kind with modulus k E.m/ or E.k/ is the complete elliptic integral of the second kind F.˛; m/ is the incomplete elliptic integral of the first kind E.˛; m/ is the incomplete elliptic integral of the second kind ƒ0 is Heuman’s Lambda function Pi is the Legendre polynomial of degree i x0 is the initial value of a variable x Coordinates and Frames x, y, z are the Cartesian (orthogonal) coordinates r, , ˛ are the spherical coordinates (radial distance, longitude, and latitude) © Springer International Publishing Switzerland 2017 171 I. I. Shevchenko, The Lidov-Kozai Effect – Applications in Exoplanet Research and Dynamical Astronomy, Astrophysics and Space Science Library 441, DOI 10.1007/978-3-319-43522-0 172 A Basic Notations In the three-body problem: r1 is the position vector of body 1 relative to body 0 r2 is the position vector of body 2 relative to the center of mass of the inner