DOCSLIB.ORG

Archimedean Tilings

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Archimedean Tilings -19- Archimedean Tilings Archimedes enumerated the convex polyhedra with regular faces and only one type of vertex (because the symmetry group is transitive on the vertices). Many people have independently enumerated the tilings of the Euclidean plane that satisfy the same condition, and a few have tried to enumerate the corresponding tilings of the hyper- bolic plane and achieved some partial results. Often there is some subgroup H of the full symmetry group G of such a tiling that remains transitive on the vertices; in this case we say that the tiling is Archimedean relative to H, to contrast it with the absolute case when H = G. For example, the Archimedean snub square tessellation (top right) has full symmetry group 4∗2, with respect to which it is absolute. However, coloring the tiles as in the second marginal figure, we see that the group 442 still acts transitively on its vertices, and so it is Archimedean relative to this subgroup. The complete classification of all Archimedean tilings, both rel- ative and absolute, appears for the first time in this book. As usual the guiding idea is that of orbifold, since once we have specified the orbifold we can recover the tiling by “unwrapping.” The orbifold of an Archimedean tiling is hard to visualize, in view of all those faces. Fortunately, we don’t have to visualize the faces, because we can remove them from the tiling with no loss of information if we’re careful. What we do is enlarge the vertices to blobs and the edges joining them to strips by slightly shrinking the faces. (One can think of these blobs and strips as the grout between the tiles.) Then we simply remove these shrunken faces! The result is like a doily made of paper (opposite page) The thirty-five relative Archimedean tilings of the Euclidean plane by squares. 251 © 2016 by Taylor & Francis Group, LLC 252 19. Archimedean Tilings circles and strips. This doily still contains all the information, since we can recover the original tessellation simply by sewing polygonal patches onto all the boundary curves. The orbifold of the doily is really quite a simple thing, since the Archimedean property of the tessellation implies that it consists of just one blob, possibly folded and probably connected to itself by various strips, again possibly folded. Below we see the doily for the snub square tessellation, with its full symmetry group 4∗2; the blob in it has five arms which are numbered 0, 1, 2, 2 ,and1 , because in the orbifold arms 1 and 2 have been folded onto 1 and 2, respectively. Also, arm 0 has been folded onto itself to become a half arm 0 . Finally, the outer ends of arms 1 and 2 have been identified, turning those arms into a band (12) that joins the blob to itself. 1 2 (12) 0 {4} 2 1 { } 0 3 What has become of the two types of faces? The square face has become the brown boundary curve, which now consists of just one edge in the orbifold; since this goes around the order-4 gyration point, we know it must have had four sides in the original, as in- dicated by our {4}. The triangle has become the purple boundary, 1 which has 1 2 sides (the full side at arms 1 and 2 and the half side at 0). But, since it ends on the red mirror line, its original polygon Downloaded by [University of Bergen Library] at 04:54 26 October 2016 was a {3}. We can convey the topological information here by the permuta- tion symbol 0 (12), (which conveys the topology), together with the face-code 34343, starting with the face between arms 0 and 1. We combine both parts into a single symbol, here 0 (12)∗(3, 4, 3, 4, 3), with the separating symbol (here ∗) indicating the local symmetry at the vertex. © 2016 by Taylor & Francis Group, LLC The Permutation Symbol 253 The Permutation Symbol In general, neighboring blobs in an archimedean tiling can be con- nected to one another by arms in just a few ways. Suppose that arm i of one blob is connected to arm i of another vertex. Then there is a symmetry fixing the central point of this edge. If there is only a rotational symmetry, of order 2, then in the orbifold we see the arm grasp an order 2 cone point: we call this a rotary arm (i). If there is a reflection symmetry interchanging the two blobs, in the orbifold we see the arm run from the vertex to a boundary of the orbifold; this is a folded band [i]. Finally, if there is a symmetry ∗2 at the center of this edge, in the orbifold we have a half arm i ,justaswesawinthesnubsquaretessellation.The type of brackets used here hints at the shape at the end of the arm. i i i i i i rotary arm (i) folded band [i] half arm i Or, we might have arm i of a blob connected to arm j = i of another blob. If there is a symmetry interchanging the two sides of this edge in the tiling, we have a half band ij , running along a boundary of the orbifold. If not, and the blobs are of the same orientation, we see an untwisted band (ij) in the orbifold, just as in the snub square tessellation. Finally, if the blobs are of opposite orientations, the orbifold will contain a twisted band [ij]. Downloaded by [University of Bergen Library] at 04:54 26 October 2016 i i i j j j untwisted band (ij) twisted band [ij] half band ij © 2016 by Taylor & Francis Group, LLC 254 19. Archimedean Tilings The parts of the orbifold that correspond to the faces we removed must each be disks; these may contain at most one cone point or kaleidoscopic point according to whether they lie in the interior of the orbifold or on its boundary, as shown on the left in the figure below. · ∗ b a n n {6a}{6b} Our separating symbol is a · if the blob lies in the interior of the orbifold, when it might become a cone point of order n,anda ∗ if it lies on a boundary of the orbifold, when it might become a Euler Characteristic kaleidoscopic point ∗n. The key observation is that an arbitrary permutation symbol If a filled in doily has f precisely describes the topology of the orbifold, up to the orders of faces and g bands (of all kinds—untwisted, twisted, cone and kaleidoscopic points! This is simply because there is just half, and folded), the Euler one way to zip disks to the boundary of the doily to get a closed − characteristic is 1+f g. surface. Half arms and rotary arms contribute nothing. This The orbifold for the symbol [0](12)[34]· is drawn below: we see number, together with the that the blob may have a cone point of order n ≥ 1 at its center. number of boundaries and the orientability of the orb- There are two boundary curves of the doily, one of which must meet ifold, determines the orb- the boundary of the orbifold. Consequently, the orbifold has exactly ifold’s topology. two faces, one with (perhaps) a cone point of order a and the other with (perhaps) a kaleidoscopic point of order b. We shall see that the values of a, b,andn can be deduced from the face code. Downloaded by [University of Bergen Library] at 04:54 26 October 2016 1 0 4 a n 2 3 b [0](12)[34]·(8b, a, 8b, 8b, 8b)n © 2016 by Taylor & Francis Group, LLC The Permutation Symbol 255 This orbifold is nonorientable with one boundary component; its Euler characteristic is 0, so the orbifold must be a M¨obius band and the tiling must have symmetry a∗b×. Moreover, counting the edges of the two faces, we see that the face code can only be (8a, 8a, 8a, b, 8a)n. Conversely, given the face code, we can deduce a, b,andn, and so know the symmetry. Consider the more complicated example 08 (1)[26](34)(57)∗. What is the corresponding orbifold? Beginning at arm 0 and tracing around, we find that the doily has two boundaries, colored purple and yellow, and so the orbifold will be filled in with two faces. It’s difficult to draw these, though! 2 1 2 0 3 9 ∗2 4 8 7 5 6 2 08(1)[26](34)(57)∗(143, 9, 148, 9, 143)2 What can we deduce about the local features of the orbifold from the symbol? There is an order-2 cone point at the end of rotary arm Downloaded by [University of Bergen Library] at 04:54 26 October 2016 (1). The boundary of the half band might have a kaleidoscopic point n at the blob, and two faces may each have cone points of orders, say, a for yellow and b for purple. The yellow face has seven edges and so will be a (7a)-gon in the tiling. The purple face has just one edge andsowillbeab-gon in the tiling. Any tiling with the permutation symbol 08 (1)[26](34)(57)∗ must therefore have a face code of the form ((7a)3,b,(7a)8,b,(7a)3)n; this immediately implies that for the face code we were given, (143, 9, 148, 9, 143)2,wehaven =2,a =2, and b =9. © 2016 by Taylor & Francis Group, LLC 256 19. Archimedean Tilings What is the orbifold’s topology? The orbifold is nonorientable because it includes the twisted band [26].
Load more

Recommended publications
  • On the Archimedean Or Semiregular Polyhedra
    ON THE ARCHIMEDEAN OR SEMIREGULAR POLYHEDRA Mark B. Villarino Depto. de Matem´atica, Universidad de Costa Rica, 2060 San Jos´e, Costa Rica May 11, 2005 Abstract We prove that there are thirteen Archimedean/semiregular polyhedra by using Euler’s polyhedral formula. Contents 1 Introduction 2 1.1 RegularPolyhedra .............................. 2 1.2 Archimedean/semiregular polyhedra . ..... 2 2 Proof techniques 3 2.1 Euclid’s proof for regular polyhedra . ..... 3 2.2 Euler’s polyhedral formula for regular polyhedra . ......... 4 2.3 ProofsofArchimedes’theorem. .. 4 3 Three lemmas 5 3.1 Lemma1.................................... 5 3.2 Lemma2.................................... 6 3.3 Lemma3.................................... 7 4 Topological Proof of Archimedes’ theorem 8 arXiv:math/0505488v1 [math.GT] 24 May 2005 4.1 Case1: fivefacesmeetatavertex: r=5. .. 8 4.1.1 At least one face is a triangle: p1 =3................ 8 4.1.2 All faces have at least four sides: p1 > 4 .............. 9 4.2 Case2: fourfacesmeetatavertex: r=4 . .. 10 4.2.1 At least one face is a triangle: p1 =3................ 10 4.2.2 All faces have at least four sides: p1 > 4 .............. 11 4.3 Case3: threefacesmeetatavertes: r=3 . ... 11 4.3.1 At least one face is a triangle: p1 =3................ 11 4.3.2 All faces have at least four sides and one exactly four sides: p1 =4 6 p2 6 p3. 12 4.3.3 All faces have at least five sides and one exactly five sides: p1 =5 6 p2 6 p3 13 1 5 Summary of our results 13 6 Final remarks 14 1 Introduction 1.1 Regular Polyhedra A polyhedron may be intuitively conceived as a “solid figure” bounded by plane faces and straight line edges so arranged that every edge joins exactly two (no more, no less) vertices and is a common side of two faces.
    [Show full text]
  • Archimedean Solids
    University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln MAT Exam Expository Papers Math in the Middle Institute Partnership 7-2008 Archimedean Solids Anna Anderson University of Nebraska-Lincoln Follow this and additional works at: https://digitalcommons.unl.edu/mathmidexppap Part of the Science and Mathematics Education Commons Anderson, Anna, "Archimedean Solids" (2008). MAT Exam Expository Papers. 4. https://digitalcommons.unl.edu/mathmidexppap/4 This Article is brought to you for free and open access by the Math in the Middle Institute Partnership at DigitalCommons@University of Nebraska - Lincoln. It has been accepted for inclusion in MAT Exam Expository Papers by an authorized administrator of DigitalCommons@University of Nebraska - Lincoln. Archimedean Solids Anna Anderson In partial fulfillment of the requirements for the Master of Arts in Teaching with a Specialization in the Teaching of Middle Level Mathematics in the Department of Mathematics. Jim Lewis, Advisor July 2008 2 Archimedean Solids A polygon is a simple, closed, planar figure with sides formed by joining line segments, where each line segment intersects exactly two others. If all of the sides have the same length and all of the angles are congruent, the polygon is called regular. The sum of the angles of a regular polygon with n sides, where n is 3 or more, is 180° x (n – 2) degrees. If a regular polygon were connected with other regular polygons in three dimensional space, a polyhedron could be created. In geometry, a polyhedron is a three- dimensional solid which consists of a collection of polygons joined at their edges. The word polyhedron is derived from the Greek word poly (many) and the Indo-European term hedron (seat).
    [Show full text]
  • Uniform Panoploid Tetracombs
    Uniform Panoploid Tetracombs George Olshevsky TETRACOMB is a four-dimensional tessellation. In any tessellation, the honeycells, which are the n-dimensional polytopes that tessellate the space, Amust by definition adjoin precisely along their facets, that is, their ( n!1)- dimensional elements, so that each facet belongs to exactly two honeycells. In the case of tetracombs, the honeycells are four-dimensional polytopes, or polychora, and their facets are polyhedra. For a tessellation to be uniform, the honeycells must all be uniform polytopes, and the vertices must be transitive on the symmetry group of the tessellation. Loosely speaking, therefore, the vertices must be “surrounded all alike” by the honeycells that meet there. If a tessellation is such that every point of its space not on a boundary between honeycells lies in the interior of exactly one honeycell, then it is panoploid. If one or more points of the space not on a boundary between honeycells lie inside more than one honeycell, the tessellation is polyploid. Tessellations may also be constructed that have “holes,” that is, regions that lie inside none of the honeycells; such tessellations are called holeycombs. It is possible for a polyploid tessellation to also be a holeycomb, but not for a panoploid tessellation, which must fill the entire space exactly once. Polyploid tessellations are also called starcombs or star-tessellations. Holeycombs usually arise when (n!1)-dimensional tessellations are themselves permitted to be honeycells; these take up the otherwise free facets that bound the “holes,” so that all the facets continue to belong to two honeycells. In this essay, as per its title, we are concerned with just the uniform panoploid tetracombs.
    [Show full text]
  • Five-Vertex Archimedean Surface Tessellation by Lanthanide-Directed Molecular Self-Assembly
    Five-vertex Archimedean surface tessellation by lanthanide-directed molecular self-assembly David Écijaa,1, José I. Urgela, Anthoula C. Papageorgioua, Sushobhan Joshia, Willi Auwärtera, Ari P. Seitsonenb, Svetlana Klyatskayac, Mario Rubenc,d, Sybille Fischera, Saranyan Vijayaraghavana, Joachim Reicherta, and Johannes V. Bartha,1 aPhysik Department E20, Technische Universität München, D-85478 Garching, Germany; bPhysikalisch-Chemisches Institut, Universität Zürich, CH-8057 Zürich, Switzerland; cInstitute of Nanotechnology, Karlsruhe Institute of Technology, D-76344 Eggenstein-Leopoldshafen, Germany; and dInstitut de Physique et Chimie des Matériaux de Strasbourg (IPCMS), CNRS-Université de Strasbourg, F-67034 Strasbourg, France Edited by Kenneth N. Raymond, University of California, Berkeley, CA, and approved March 8, 2013 (received for review December 28, 2012) The tessellation of the Euclidean plane by regular polygons has by five interfering laser beams, conceived to specifically address been contemplated since ancient times and presents intriguing the surface tiling problem, yielded a distorted, 2D Archimedean- aspects embracing mathematics, art, and crystallography. Sig- like architecture (24). nificant efforts were devoted to engineer specific 2D interfacial In the last decade, the tools of supramolecular chemistry on tessellations at the molecular level, but periodic patterns with surfaces have provided new ways to engineer a diversity of sur- distinct five-vertex motifs remained elusive. Here, we report a face-confined molecular architectures, mainly exploiting molecular direct scanning tunneling microscopy investigation on the cerium- recognition of functional organic species or the metal-directed directed assembly of linear polyphenyl molecular linkers with assembly of molecular linkers (5). Self-assembly protocols have terminal carbonitrile groups on a smooth Ag(111) noble-metal sur- been developed to achieve regular surface tessellations, includ- face.
    [Show full text]
  • Snubs, Alternated Facetings, & Stott-Coxeter-Dynkin Diagrams
    Symmetry: Culture and Science Vol. 21, No.4, 329-344, 2010 SNUBS, ALTERNATED FACETINGS, & STOTT-COXETER-DYNKIN DIAGRAMS Dr. Richard Klitzing Non-professional mathematician, (b. Laupheim, BW., Germany, 1966). Address: Kantstrasse 23, 89522 Heidenheim, Germany. E-mail: [email protected] . Fields of interest: Polytopes, geometry, mathematical quasi-crystallography. Publications: (2002) Axial Symmetrical Edge-Facetings of Uniform Polyhedra. In: Symmetry: Cult. & Sci., vol. 13, nos. 3- 4, pp. 241-258. (2001) Convex Segmentochora. In: Symmetry: Cult. & Sci., vol. 11, nos. 1-4, pp. 139-181. (1996) Reskalierungssymmetrien quasiperiodischer Strukturen. [Symmetries of Rescaling for Quasiperiodic Structures, Ph.D. Dissertation, in German], Eberhard-Karls-Universität Tübingen, or Hamburg, Verlag Dr. Kovač, ISBN 978-3-86064-428- 7. – (Former ones: mentioned therein.) Abstract: The snub cube and the snub dodecahedron are well-known polyhedra since the days of Kepler. Since then, the term “snub” was applied to further cases, both in 3D and beyond, yielding an exceptional species of polytopes: those do not bow to Wythoff’s kaleidoscopical construction like most other Archimedean polytopes, some appear in enantiomorphic pairs with no own mirror symmetry, etc. However, they remained stepchildren, since they permit no real one-step access. Actually, snub polytopes are meant to be derived secondarily from Wythoffians, either from omnitruncated or from truncated polytopes. – This secondary process herein is analysed carefully and extended widely: nothing bars a progress from vertex alternation to an alternation of an arbitrary class of sub-dimensional elements, for instance edges, faces, etc. of any type. Furthermore, this extension can be coded in Stott-Coxeter-Dynkin diagrams as well.
    [Show full text]
  • Convex Polytopes and Tilings with Few Flag Orbits
    Convex Polytopes and Tilings with Few Flag Orbits by Nicholas Matteo B.A. in Mathematics, Miami University M.A. in Mathematics, Miami University A dissertation submitted to The Faculty of the College of Science of Northeastern University in partial fulfillment of the requirements for the degree of Doctor of Philosophy April 14, 2015 Dissertation directed by Egon Schulte Professor of Mathematics Abstract of Dissertation The amount of symmetry possessed by a convex polytope, or a tiling by convex polytopes, is reflected by the number of orbits of its flags under the action of the Euclidean isometries preserving the polytope. The convex polytopes with only one flag orbit have been classified since the work of Schläfli in the 19th century. In this dissertation, convex polytopes with up to three flag orbits are classified. Two-orbit convex polytopes exist only in two or three dimensions, and the only ones whose combinatorial automorphism group is also two-orbit are the cuboctahedron, the icosidodecahedron, the rhombic dodecahedron, and the rhombic triacontahedron. Two-orbit face-to-face tilings by convex polytopes exist on E1, E2, and E3; the only ones which are also combinatorially two-orbit are the trihexagonal plane tiling, the rhombille plane tiling, the tetrahedral-octahedral honeycomb, and the rhombic dodecahedral honeycomb. Moreover, any combinatorially two-orbit convex polytope or tiling is isomorphic to one on the above list. Three-orbit convex polytopes exist in two through eight dimensions. There are infinitely many in three dimensions, including prisms over regular polygons, truncated Platonic solids, and their dual bipyramids and Kleetopes. There are infinitely many in four dimensions, comprising the rectified regular 4-polytopes, the p; p-duoprisms, the bitruncated 4-simplex, the bitruncated 24-cell, and their duals.
    [Show full text]
  • Local Symmetry Preserving Operations on Polyhedra
    Local Symmetry Preserving Operations on Polyhedra Pieter Goetschalckx Submitted to the Faculty of Sciences of Ghent University in fulfilment of the requirements for the degree of Doctor of Science: Mathematics. Supervisors prof. dr. dr. Kris Coolsaet dr. Nico Van Cleemput Chair prof. dr. Marnix Van Daele Examination Board prof. dr. Tomaž Pisanski prof. dr. Jan De Beule prof. dr. Tom De Medts dr. Carol T. Zamfirescu dr. Jan Goedgebeur © 2020 Pieter Goetschalckx Department of Applied Mathematics, Computer Science and Statistics Faculty of Sciences, Ghent University This work is licensed under a “CC BY 4.0” licence. https://creativecommons.org/licenses/by/4.0/deed.en In memory of John Horton Conway (1937–2020) Contents Acknowledgements 9 Dutch summary 13 Summary 17 List of publications 21 1 A brief history of operations on polyhedra 23 1 Platonic, Archimedean and Catalan solids . 23 2 Conway polyhedron notation . 31 3 The Goldberg-Coxeter construction . 32 3.1 Goldberg ....................... 32 3.2 Buckminster Fuller . 37 3.3 Caspar and Klug ................... 40 3.4 Coxeter ........................ 44 4 Other approaches ....................... 45 References ............................... 46 2 Embedded graphs, tilings and polyhedra 49 1 Combinatorial graphs .................... 49 2 Embedded graphs ....................... 51 3 Symmetry and isomorphisms . 55 4 Tilings .............................. 57 5 Polyhedra ............................ 59 6 Chamber systems ....................... 60 7 Connectivity .......................... 62 References
    [Show full text]
  • Operation-Based Notation for Archimedean Graph
    Operation-Based Notation for Archimedean Graph Hidetoshi Nonaka Research Group of Mathematical Information Science Division of Computer Science, Hokkaido University N14W9, Sapporo, 060 0814, Japan ABSTRACT Table 1. The list of Archimedean solids, where p, q, r are the number of vertices, edges, and faces, respectively. We introduce three graph operations corresponding to Symbol Name of polyhedron p q r polyhedral operations. By applying these operations, thirteen Archimedean graphs can be generated from Platonic graphs that A(3⋅4)2 Cuboctahedron 12 24 14 are used as seed graphs. A4610⋅⋅ Great Rhombicosidodecahedron 120 180 62 A468⋅⋅ Great Rhombicuboctahedron 48 72 26 Keyword: Archimedean graph, Polyhedral graph, Polyhedron A 2 Icosidodecahedron 30 60 32 notation, Graph operation. (3⋅ 5) A3454⋅⋅⋅ Small Rhombicosidodecahedron 60 120 62 1. INTRODUCTION A3⋅43 Small Rhombicuboctahedron 24 48 26 A34 ⋅4 Snub Cube 24 60 38 Archimedean graph is a simple planar graph isomorphic to the A354 ⋅ Snub Dodecahedron 60 150 92 skeleton or wire-frame of the Archimedean solid. There are A38⋅ 2 Truncated Cube 24 36 14 thirteen Archimedean solids, which are semi-regular polyhedra A3⋅102 Truncated Dodecahedron 60 90 32 and the subset of uniform polyhedra. Seven of them can be A56⋅ 2 Truncated Icosahedron 60 90 32 formed by truncation of Platonic solids, and all of them can be A 2 Truncated Octahedron 24 36 14 formed by polyhedral operations defined as Conway polyhedron 4⋅6 A 2 Truncated Tetrahedron 12 18 8 notation [1-2]. 36⋅ The author has recently developed an interactive modeling system of uniform polyhedra including Platonic solids, Archimedean solids and Kepler-Poinsot solids, based on graph drawing and simulated elasticity, mainly for educational purpose [3-5].
    [Show full text]
  • A Recursive Algorithm for the K-Face Numbers of Wythoffian-N-Polytopes Constructed from Regular Polytopes
    Journal of Information Processing Vol.25 528–536 (Aug. 2017) [DOI: 10.2197/ipsjjip.25.528] Invited Paper A recursive Algorithm for the k-face Numbers of Wythoffian-n-polytopes Constructed from Regular Polytopes Jin Akiyama1,a) Sin Hitotumatu2 Motonaga Ishii3,b) Akihiro Matsuura4,c) Ikuro Sato5,d) Shun Toyoshima6,e) Received: September 6, 2016, Accepted: May 25, 2017 Abstract: In this paper, an n-dimensional polytope is called Wythoffian if it is derived by the Wythoff construction from an n-dimensional regular polytope whose finite reflection group belongs to An,Bn,Cn,F4,G2,H3,H4 or I2(p). Based on combinatorial and topological arguments, we give a matrix-form recursive algorithm that calculates the num- ber of k-faces (k = 0, 1,...,n) of all the Wythoffian-n-polytopes using Schlafli-Wytho¨ ff symbols. The correctness of the algorithm is reconfirmed by the method of exhaustion using a computer. Keywords: Wythoff construction, Wythoffian polytopes, k-face numbers, recursive algorithm, Coxeter group ( c ) volumes and surface areas. 1. Introduction Our purpose has been completed and already implemented High-dimensional polytopes have been studied mainly by the as computer programs. We will introduce a new methodology following methodologies: to study volumes, surface areas, number of k-faces sharing a (1) Combinatorics and Topology, (2) Graph Theory, (3) Group vertex, etc. of Wythoffian-n-polytopes constructed from regular Theory and (4) Metric Geometry. See [1], [2], [8], [9], [10], [11], polytopes in the forthcoming papers. In this paper, as a first [14], [15], [18], [19] for some background researches on tilings, step, we develop a recursive algorithm that computes the f-vector lattices and polytopes.
    [Show full text]
  • Naming Archimedean and Catalan Polyhedra and Tilings
    -21- Naming Archimedean and Catalan Polyhedra and Tilings The book in which Archimedes enumerated the polyhedra that have regular faces and equivalent vertices is unfortunately lost; however, its contents were reconstructed by Kepler, from whom the tradi- tional names descend. In this chapter we explain these “Keplerian” names for the Archimedean and Catalan solids and extend them to the analogous tessellations of two- and three-dimensional Euclidean space. We shall describe the polyhedra in dual pairs indicated by the ar- rows, and at the same time give our abbreviations for them, starting with the five Platonic (or regular) ones: TC↔ OD↔ I Tetrahedron Cube Octahedron Dodecahedron Icosahedron Etymologically, the Greek stem “hedr-” is cognate with the Latin “sede-” and the English “seat,” so that, for instance, “dodecahedron” really means “twelve-seater.” (opposite page) The Archimedean solids and their duals can be nicely arranged so that their edges are mutually tangent, at their intersections, to a common sphere. 283 © 2016 by Taylor & Francis Group, LLC 284 21. Naming Archimedean and Catalan Polyhedra and Tilings Truncation and “Kis”ing These are followed by their “truncated” and “kis-” versions. Here, truncation means cutting off the corners in such a way that each regular n-gonal face is replaced by a regular 2n-gonal one. The dual operation is to erect a pyramid on each face, thus replacing a regular m-gon by m isoceles triangles. These give five Archimedean and five Catalan solids: truncated truncated truncated truncated truncated Tetrahedron Cube Octahedron Dodecahedron Icosahedron tT tC tO tD tI kT kC kO kD kI kisTetrahedron kisCube kisOctahedron kisDodecahedron kisIcosahedron The names used by Kepler for the Catalan ones were rather longer, namely, triakis tetrakis triakis pentakis triakis Downloaded by [University of Bergen Library] at 04:55 26 October 2016 tetrahedron hexahedron octahedron dodecahedron icosahedron and were usually printed as single words.
    [Show full text]
  • Erik Demaine Martin Demaine Anna Lubiw Arlo Shallit Jonah Shallit
    Zipper Unfoldings of Polyhedral Complexes Erik Demaine Martin Demaine Anna Lubiw Arlo Shallit Jonah Shallit Thursday, August 12, 2010 1 Unfolding Polyhedra—Durer 1400’s Durer, 1498 snub cube Thursday, August 12, 2010 2 Unfolding Polyhedra—Octahedron all unfoldings Thursday, August 12, 2010 3 Thursday, August 12, 2010 4 Zipper Unfoldings of Polyhedra—Octahedron Thursday, August 12, 2010 5 Zippers separating zipper multiple toggles (cosmetic) Thursday, August 12, 2010 6 Zippers • 1891 patent by Whitcomb Judson • novel, but not practical (“If skirt is to be washed, remove fastener.”) • named “zipper” by B.F. Goodrich company in 1920’s • ubiquitous but super!uous Thursday, August 12, 2010 7 Edge Cuts versus Face Cuts edge cuts face cuts Zipper edge cuts = Hamiltonian unfolding [Shepherd ’75] Thursday, August 12, 2010 8 Zipper Edge Cuts (Hamiltonian Unfolding) What is a zipper unfolding of a polyhedron? on the polyhedron the cut is a simple path on the polygon this is forbidden Nick Chase Thursday, August 12, 2010 9 Outline of Talk Convex Polyhedra Platonic Solids Archimedean Solids Polyhedral Manifolds Polyhedral Complexes Thursday, August 12, 2010 10 Platonic Solids Thursday, August 12, 2010 12 Platonic Solids "ese are doubly Hamiltonian—the cut is a path and faces are joined in a path. Thursday, August 12, 2010 13 great rhombicosi- Archimedean Solids dodecahedron truncated truncated tetrahedron dodeca- hedron truncated truncated icosa- cube hedron great truncated rhombicub- octahedron octahedron small cubocta- rhombicosi- hedron dodecahedron
    [Show full text]
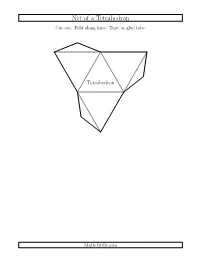
  • Geometry Worksheet -- Nets of Platonic and Archimedean Solids
    Net of a Tetrahedron Cut out. Fold along lines. Tape or glue tabs. Tetrahedron Math-Drills.com Net of a Cube Cut out. Fold along lines. Tape or glue tabs. Cube Math-Drills.com Net of an Octahedron Cut out. Fold along lines. Tape or glue tabs. Octahedron Math-Drills.com Net of a Dodecahedron 1 Cut out. Fold along lines. Tape or glue tabs. Dodecahedron Math-Drills.com Net of a Dodecahedron 2 Cut out. Fold along lines. Tape or glue tabs. Dodecahedron Math-Drills.com Net of an Icosahedron Cut out. Fold along lines. Tape or glue tabs. Icosahedron Math-Drills.com Net of a Truncated Tetrahedron Cut out. Fold along lines. Tape or glue tabs. Truncated Tetrahedron Math-Drills.com Net of a Cuboctahedron Cut out. Fold along lines. Tape or glue tabs. Cuboctahedron Math-Drills.com Net of a Truncated Cube Cut out. Fold along lines. Tape or glue tabs. Truncated Cube Math-Drills.com Net of a Truncated Octahedron Cut out. Fold along lines. Tape or glue tabs. Truncated Octahedron Math-Drills.com Net of a Rhombicuboctahedron Cut out. Fold along lines. Tape or glue tabs. Rhombi- cuboctahedron Math-Drills.com Net of a Truncated Cuboctahedron Cut out. Fold along lines. Tape or glue tabs. Truncated Cuboctahedron Math-Drills.com Net of a Snub Cube Cut out. Fold along lines. Tape or glue tabs. Snub Cube Math-Drills.com Net of an Icosidodecahedron Cut out. Fold along lines. Tape or glue tabs. Icosidodecahedron Math-Drills.com.
    [Show full text]