DOCSLIB.ORG

Computational Geometry · Lecture Line Segment Intersection

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Computational Geometry · Lecture Line Segment Intersection Computational Geometry · Lecture Line Segment Intersection INSTITUT FUR¨ THEORETISCHE INFORMATIK · FAKULTAT¨ FUR¨ INFORMATIK Tamara Mchedlidze · Darren Strash 26.10.2015 1 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection Aside: Organizational Items 2 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection Overlaying Map Layers Example: Given two different map layers whose intersection is of interest. Land use + Precipitation = Map combining themes 3 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection Overlaying Map Layers Example: Given two different map layers whose intersection is of interest. Land use + Precipitation = Map combining themes Regions are polygons Polygons are line segments Calculate all line segment intersections Compute regions 3 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection Problem Formulation Given: Set S = fs1; : : : ; sng of line segments in the plane Output: all intersections of two or more line segments for each intersection, the line segments involved. 4 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection Problem Formulation Given: Set S = fs1; : : : ; sng of line segments in the plane Output: all intersections of two or more line segments for each intersection, the line segments involved. Def: Line segments are closed 4 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection Problem Formulation Given: Set S = fs1; : : : ; sng of line segments in the plane Output: all intersections of two or more line segments for each intersection, the line segments involved. Def: Line segments are closed Discussion: { How can you solve this problem naively? { Is this already optimal? { Are their better approaches? 4 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection The Sweep-Line Method: An Example 5 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection The Sweep-Line Method: An Example Events 5 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection The Sweep-Line Method: An Example 5 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection The Sweep-Line Method: An Example sweep line 5 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection The Sweep-Line Method: An Example 5 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection The Sweep-Line Method: An Example 5 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection The Sweep-Line Method: An Example 5 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection The Sweep-Line Method: An Example 5 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection The Sweep-Line Method: An Example 5 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection The Sweep-Line Method: An Example 5 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection The Sweep-Line Method: An Example 5 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection The Sweep-Line Method: An Example 5 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection The Sweep-Line Method: An Example 5 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection The Sweep-Line Method: An Example 5 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection The Sweep-Line Method: An Example 5 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection The Sweep-Line Method: An Example 5 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection The Sweep-Line Method: An Example 5 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection The Sweep-Line Method: An Example 5 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection The Sweep-Line Method: An Example 5 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection The Sweep-Line Method: An Example 5 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection The Sweep-Line Method: An Example 5 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection The Sweep-Line Method: An Example 5 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection Data Structures 1.) Event Queue Q define p ≺ q ,def: yp > yq _ (yp = yq ^ xp < xq) p q ` 6 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection Data Structures 1.) Event Queue Q define p ≺ q ,def: yp > yq _ (yp = yq ^ xp < xq) p q ` Store events by ≺ in a balanced binary search tree ! e.g., AVL tree, red-black tree, . 6 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection Data Structures 1.) Event Queue Q define p ≺ q ,def: yp > yq _ (yp = yq ^ xp < xq) p q ` Store events by ≺ in a balanced binary search tree ! e.g., AVL tree, red-black tree, . Operations insert, delete and nextEvent in O(log jQj) time 6 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection Data Structures 1.) Event Queue Q define p ≺ q ,def: yp > yq _ (yp = yq ^ xp < xq) p q ` Store events by ≺ in a balanced binary search tree ! e.g., AVL tree, red-black tree, . Operations insert, delete and nextEvent in O(log jQj) time 2.) Sweep-Line Status T ` Stores ` cut lines ordered from left to right 6 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection Data Structures 1.) Event Queue Q define p ≺ q ,def: yp > yq _ (yp = yq ^ xp < xq) p q ` Store events by ≺ in a balanced binary search tree ! e.g., AVL tree, red-black tree, . Operations insert, delete and nextEvent in O(log jQj) time 2.) Sweep-Line Status T ` Stores ` cut lines ordered from left to right Required operations insert, delete, findNeighbor 6 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection Data Structures 1.) Event Queue Q define p ≺ q ,def: yp > yq _ (yp = yq ^ xp < xq) p q ` Store events by ≺ in a balanced binary search tree ! e.g., AVL tree, red-black tree, . Operations insert, delete and nextEvent in O(log jQj) time 2.) Sweep-Line Status T ` Stores ` cut lines ordered from left to right Required operations insert, delete, findNeighbor This is also a balanced binary search tree with line segments stored in the leaves! 6 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection Algorithm FindIntersections(S) Input: Set S of line segments Output: Set of all intersection points and the line segments involved Q ;; T ; foreach s 2 S do Q.insert(upperEndPoint(s)) Q.insert(lowerEndPoint(s)) while Q= 6 ; do p Q:nextEvent() Q.deleteEvent(p) handleEvent(p) 7 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection Algorithm FindIntersections(S) Input: Set S of line segments Output: Set of all intersection points and the line segments involved Q ;; T ; foreach s 2 S do Q.insert(upperEndPoint(s)) What happens Q.insert(lowerEndPoint(s)) with duplicates? while Q= 6 ; do p Q:nextEvent() Q.deleteEvent(p) handleEvent(p) 7 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection Algorithm FindIntersections(S) Input: Set S of line segments Output: Set of all intersection points and the line segments involved Q ;; T ; foreach s 2 S do Q.insert(upperEndPoint(s)) What happens Q.insert(lowerEndPoint(s)) with duplicates? while Q= 6 ; do p Q:nextEvent() Q.deleteEvent(p) handleEvent(p) This is the core of the algorithm! 7 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection Algorithm handleEvent(p) U(p) Line segments with p as upper endpoint L(p) Line segments with p as lower endpoint C(p) Line segments with p as interior point if jU(p) [ L(p) [ C(p)j ≥ 2 then return p and U(p) [ L(p) [ C(p) remove L(p) [ C(p) from T add U(p) [ C(p) to T if U(p) [ C(p) = ; then //sl and sr, neighbors of p in T Q check if sl and sr intersect below p else //s0 and s00 leftmost and rightmost line segment in U(p) [ C(p) 0 Q check if sl and s intersect below p 00 Q check if sr and s intersect below p 8 Dr. Tamara Mchedlidze · Dr. Darren Strash · Computational Geometry Lecture Line Segment Intersection Algorithm handleEvent(p) U(p) Line segments with p as upper endpointStored with p in Q L(p) Line segments with p as lower endpoint C(p) Line segments with p as interior point if jU(p) [ L(p) [ C(p)j ≥ 2 then return p and U(p) [ L(p) [ C(p) remove L(p) [ C(p) from T add U(p) [ C(p) to T if U(p) [ C(p) = ; then //sl and sr, neighbors of p in T Q check if sl and sr intersect below p else //s0 and s00 leftmost and rightmost line segment in U(p) [ C(p) 0 Q check
Load more

Recommended publications
  • Sweeping the Sphere
    Sweeping the Sphere Joao˜ Dinis Margarida Mamede Departamento de F´ısica CITI, Departamento de Informatica´ Faculdade de Ciencias,ˆ Universidade de Lisboa Faculdade de Cienciasˆ e Tecnologia, FCT Campo Grande, Edif´ıcio C8 Universidade Nova de Lisboa 1749-016 Lisboa, Portugal 2829-516 Caparica, Portugal [email protected] [email protected] Abstract—We introduce the first sweep line algorithm for and Hong [5], [6], which is O(n log n) worst case optimal, computing spherical Voronoi diagrams, which proves that where n is the number of sites. An asymptotically slower Fortune’s method can be extended to points on a sphere alternative in the worst case is the randomized incremental surface. This algorithm is similar to Fortune’s plane sweep algorithm, sweeping the sphere with a circular line instead of algorithm of Clarkson and Shor [7], whose expected running a straight one. time is O(n log n). The well-known Quickhull algorithm of Like its planar counterpart, the novel linear-space algorithm Barber et al. [8] can be seen as an efficient variation of the has worst-case optimal running time. Furthermore, it copes previous algorithm. very well with degeneracies and is easy to implement. Experi- A different approach is to adapt the randomized incremen- mental results show that the performance of our algorithm is very similar to that of Fortune’s algorithm, both with synthetic tal algorithm that computes the planar Delaunay triangula- data sets and with real data. tion [9], [10]. The essential operation used in the incremental The usual solutions make use of the connection between step, which checks if a circle defined by three sites contains a convex hulls and spherical Delaunay triangulations.
    [Show full text]
  • Uwaterloo Latex Thesis Template
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by University of Waterloo's Institutional Repository Approximation Algorithms for Geometric Covering Problems for Disks and Squares by Nan Hu A thesis presented to the University of Waterloo in fulfillment of the thesis requirement for the degree of Master of Mathematics in Computer Science Waterloo, Ontario, Canada, 2013 c Nan Hu 2013 I hereby declare that I am the sole author of this thesis. This is a true copy of the thesis, including any required final revisions, as accepted by my examiners. I understand that my thesis may be made electronically available to the public. ii Abstract Geometric covering is a well-studied topic in computational geometry. We study three covering problems: Disjoint Unit-Disk Cover, Depth-(≤ K) Packing and Red-Blue Unit- Square Cover. In the Disjoint Unit-Disk Cover problem, we are given a point set and want to cover the maximum number of points using disjoint unit disks. We prove that the problem is NP-complete and give a polynomial-time approximation scheme (PTAS) for it. In Depth-(≤ K) Packing for Arbitrary-Size Disks/Squares, we are given a set of arbitrary-size disks/squares, and want to find a subset with depth at most K and maxi- mizing the total area. We prove a depth reduction theorem and present a PTAS. In Red-Blue Unit-Square Cover, we are given a red point set, a blue point set and a set of unit squares, and want to find a subset of unit squares to cover all the blue points and the minimum number of red points.
    [Show full text]
  • Visibility Graphs and Cell Decompositions
    Visibility Graphs and Cell Decompositions CIS 390 Kostas Daniilidis With material from Chapter 5 - Roadmaps Principles of Robot Motion: Theory, Algorithms, and Implementation by Howie ChosetÂet al. The MIT Press © 2005 For polygonal obstacles in 2D • Assume robot is a point • Any shortest path from start to goal among a set of disjoint polygonal obstacles is a polygonal path whose inner vertices are convex vertices of the obstacles (imagine a tight rope from start to end) Visibility graph • Vertices: all vertices of the polygonal obstacles plus the start and the goal • Edges: all line segments between vertices that do not intersect obstacles • It is not a planar graph: edges are crossing (not at vertices) Visibility graph construction • Brute force O(n^3) algorithm visits – all n vertices – applies a rotational plane sweep that connects with all other n vertices – and determines whether each segment intersects any of the O(n) edges • We can do better by sorting the vertices. Sweep Line Algorithm • Input: A set of vertices {νi} (whose edges do not intersect) and a vertex ν • Output: A subset of vertices from {νi} that are within line of sight of ν • 1: For each vertex vi, calculate αi, the angle from the horizontal axis to the line segment • ννi. • 2: Create the vertex list E , containing the αi 's sorted in increasing order. • 3: Create the active list S, containing the sorted list of edges that intersect the horizontal • half-line emanating from ν. • 4: for all αi do • 5: if νi is visible to ν then • 6: Add the edge (ν, νi )to the visibility graph.
    [Show full text]
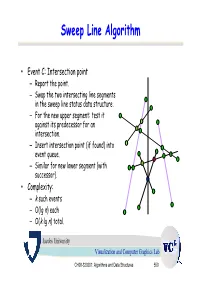
  • Sweep Line Algorithm
    Sweep Line Algorithm • Event C: Intersection point – Report the point. – Swap the two intersecting line segments in the sweep line status data structure. – For the new upper segment: test it against its predecessor for an intersection. – Insert intersection point (if found) into event queue. – Similar for new lower segment (with successor). • Complexity: – k such events – O(lg n) each – O(k lg n) total. Jacobs University Visualization and Computer Graphics Lab CH08-320201: Algorithms and Data Structures 550 Example a3 b4 Sweep Line status: s3 e1 s4 s0, s1, s2, s3 Event Queue: a2 a4 b3 a4, b1, b2, b0, b3, b4 s2 b1 b0 s1 b2 s0 a1 a0 Jacobs University Visualization and Computer Graphics Lab CH08-320201: Algorithms and Data Structures 551 Example a3 b4 Actions: s3 Insert s4 to SLS e1 s4 Test s4-s3 and s4-s2. a2 a4 b3 Add e1 to EQ s2 b1 Sweep Line status: b0 s1 b2 s0, s1, s2, s4, s3 s0 a1 a0 Event Queue: b1, e1, b2, b0, b3, b4 Jacobs University Visualization and Computer Graphics Lab CH08-320201: Algorithms and Data Structures 552 Example a3 b4 Actions: s3 e1 s4 Delete s1 from SLS Test s0-s2. a2 a4 b3 Add e2 to EQ s2 Sweep Line status: e2 b0 b1 s1 b2 s0, s2, s4, s3 s0 a1 a0 Event Queue: e1, e2, b2, b0, b3, b4 Jacobs University Visualization and Computer Graphics Lab CH08-320201: Algorithms and Data Structures 553 Example a3 b4 Actions: s3 e1 s4 Swap s3 and s4 in SLS Test s3-s2.
    [Show full text]
  • Parallel Range, Segment and Rectangle Queries with Augmented Maps
    Parallel Range, Segment and Rectangle Queries with Augmented Maps Yihan Sun Guy E. Blelloch Carnegie Mellon University Carnegie Mellon University [email protected] [email protected] Abstract The range, segment and rectangle query problems are fundamental problems in computational geometry, and have extensive applications in many domains. Despite the significant theoretical work on these problems, efficient implementations can be complicated. We know of very few practical implementations of the algorithms in parallel, and most implementations do not have tight theoretical bounds. In this paper, we focus on simple and efficient parallel algorithms and implementations for range, segment and rectangle queries, which have tight worst-case bound in theory and good parallel performance in practice. We propose to use a simple framework (the augmented map) to model the problem. Based on the augmented map interface, we develop both multi-level tree structures and sweepline algorithms supporting range, segment and rectangle queries in two dimensions. For the sweepline algorithms, we also propose a parallel paradigm and show corresponding cost bounds. All of our data structures are work-efficient to build in theory (O(n log n) sequential work) and achieve a low parallel depth (polylogarithmic for the multi-level tree structures, and O(n) for sweepline algorithms). The query time is almost linear to the output size. We have implemented all the data structures described in the paper using a parallel augmented map library. Based on the library each data structure only requires about 100 lines of C++ code. We test their performance on large data sets (up to 108 elements) and a machine with 72-cores (144 hyperthreads).
    [Show full text]
  • Variations of Enclosing Problem Using Axis Parallel Square(S): a General Approach
    American Journal of Computational Mathematics, 2014, 4, 197-205 Published Online June 2014 in SciRes. http://www.scirp.org/journal/ajcm http://dx.doi.org/10.4236/ajcm.2014.43016 Variations of Enclosing Problem Using Axis Parallel Square(s): A General Approach Priya Ranjan Sinha Mahapatra Department of Computer Science and Engineering, University of Kalyani, Kalyani, India Email: [email protected] Received 16 December 2013; revised 6 January 2014; accepted 15 January 2014 Copyright © 2014 by author and Scientific Research Publishing Inc. This work is licensed under the Creative Commons Attribution International License (CC BY). http://creativecommons.org/licenses/by/4.0/ Abstract Let P be a set of n points in two dimensional plane. For each point pP∈ , we locate an axis- parallel unit square having one particular side passing through p and enclosing the maximum number of points from P . Considering all points pP∈ , such n squares can be reported in On( log n) time. We show that this result can be used to (i) locate m (> 2) axis-parallel unit squares which are pairwise disjoint and they together enclose the maximum number of points from P (if exists) and (ii) find the smallest axis-parallel square enclosing at least k points of P , 2 ≤≤kn. Keywords Axis-Parallel Unit Square, Sweep Line Algorithm, Maximium Enclosing Problem, K-Enclosing Problem 1. Introduction Given a set P= { pp12,,, pn } points in a plane, enclosing problem in computational geometry is concerned with finding the smallest geometrical object of a given type that encloses all the points of P . Some well known instances of the enclosing problem are finding minimum enclosing circle [1], minimum area triangle [2], minimum area rectangle [3], minimum bounding box [4], and smallest width annulus [5].
    [Show full text]
  • Geometric Search·Intersection
    6.3 Geometric Search Overview Geometric objects. Points, lines, intervals, circles, rectangles, polygons, ... This lecture. Intersection among N objects. Example problems. • 1D range search. • 2D range search. • Find all intersections among h-v line segments. ‣ range search • Find all intersections among h-v rectangles. ‣ space partitioning trees ‣ intersection search th Algorithms in Java, 4 Edition · Robert Sedgewick and Kevin Wayne · Copyright © 2009 · January 26, 2010 8:49:21 AM 2 1d range search Extension of ordered symbol table. • Insert key-value pair. • Search for key k. • Rank: how many keys less than k? • Range search: find all keys between k1 and k2. Application. Database queries. ‣ range search ‣ space partitioning trees insert B B ‣ intersection search Geometric interpretation. insert D B D Keys are point on a line. insert A A B D • insert I A B D I • How many points in a given interval? insert H A B D H I insert F A B D F H I insert P A B D F H I P count G to K 2 search G to K H I 3 4 1d range search: implementations 1d range search: BST implementation Ordered array. Slow insert, binary search for lo and hi to find range. Range search. Find all keys between lo and hi? Hash table. No reasonable algorithm (key order lost in hash). • Recursively find all keys in left subtree (if any could fall in range). • Check key in current node. • Recursively find all keys in right subtree (if any could fall in range). data structure insert rank range count range search searching in the range [F..T] red keys are used in compares ordered array N log N log N R + log N but are not in the range S hash table 1 N N N E X A R BST log N log N log N R + log N C H M L P black keys are N = # keys in the range R = # keys that match Range search in a BST BST.
    [Show full text]
  • CSC-758: Computational Geometry Course Description
    UNIVERSITY OF NEVADA LAS VEGAS Department of Computer Science CSC-758: Computational Geometry Course Description Computational geometry deals with the development and analysis of algorithms having geometric flavor. Knowledge of elementary data structures (arrays, heaps, balanced trees, etc) and algorithmic tools (asymptotic analysis, space time complexity, divide and conquer, dynamic programming, etc) are prerequisites for this course. Student Learning Outcomes The learning outcomes for the course. • Elementary geometric methods: points, lines and polygons. Line segments intersection. Simple closed path, inclusion in a polygon, inclusion in a convex polygon, range search, point location in planar subdivision and duality. • Convex hull: Graham's scan, Jarvin's march, divide and conquer approach, on-line algorithms, approximate algorithms, convex hull of simple polygons, lower bound proofs and diameter of a point set. • Proximity: Closest pair, triangulation, divide and conquer approach for closest pair, Voronoi diagram and their properties, dual of Voronoi diagram, construction of Voronoi diagram, Euclidean minimum spanning tree, gaps and covers. • Intersections: convex polygons, polygons, star polygons, line segments, half planes and plane sweep paradigm. • Mesh generation algorithms: Delaunay triangulation, quad-trees, and Quadrangulations. • Visibility and path planning: visibility properties of polygons, visibility graphs, applications of computational geometry in robotics, shortest s-t path inside a simple polygon, shortest s-t path
    [Show full text]
  • 18.415 Advanced Algorithms Contents
    18.415 Advanced Algorithms Notes from Fall 2020. Last Updated: November 27, 2020. Contents Introduction 6 1 Lecture 1: Fibonacci Heaps7 1.1 MST problem review.................................7 1.2 Using d-heaps for MST................................8 1.3 Introduction to Fibonacci Heaps...........................8 2 Lecture 2: Fibonacci Heaps, Persistent Data Structs 12 2.1 Fibonacci Heaps Continued.............................. 12 2.2 Applications of Fibonacci Heaps........................... 14 2.2.1 Further Improvements............................ 15 2.3 Introduction to Persistent Data Structures...................... 15 3 Lecture 3: Persistent Data Structs, Splay Trees 16 3.1 Persistent Data Structures Continued........................ 16 3.2 The Planar Point Location Problem......................... 17 3.3 Introduction to Splay Trees.............................. 19 4 Lecture 4: Splay Trees 20 4.1 Heuristics of Splay Trees............................... 20 4.2 Solving the Balancing Problem............................ 20 4.3 Implementation and Analysis of Operations..................... 21 4.4 Results with the Access Lemma........................... 23 5 Lecture 5: Splay Updates, Buckets 25 5.1 Wrapping up Splay Trees............................... 25 5.2 Buckets and Indirect Addressing........................... 26 5.2.1 Improvements................................. 27 5.2.2 Formalization with Tries........................... 27 5.2.3 Laziness wins again.............................. 28 1 6 Lecture 6: VEB queues, Hashing 29 6.1 Improvements
    [Show full text]
  • A Divide and Conquer Algorithm for Rectilinear Region Coverage
    Proceedings of the 2004 IEEE Conference on Robotics, Automation and Mechatronics Singapore, 1-3 December, 2004 A Divide and Conquer Algorithm for Rectilinear Region Coverage Amit Agarwal, Meng-Hiot Lim, Lip Chien Woon Intelligent Systems Center, Techno Plaza Nanyang Technological University Singapore 639798 {pg0212208t, emhlim, 810301075597}@ntu.edu.sg Ablitract-We give algorithm to generate coverage motion an a example, see [6]). Due to this, scalable efficient algorithms plan for a single unmanned reconnaissance aerial vehicle that treat the region to be covered as an undivided whole will over rectilinear polygonal region. is (URAV) a holed The URAV likely remain elusive (unless P=NP). Thus, an alternative equipped with a stabilized downward-looking sensor which has a solution strategy is needed. In this work, we describe a divide- square footprint of a fixed area. The algorithm is based on the and-conquer algorithm for covering a rectilinear polygon. principle of divide-and-conquer. In the tirst step, we generate the More specifically, our algorithm is invariant to the presence of lexicographically maximum area rectangle partition of the hole(s) in the polygon . The underlying polygon need not be polygon. We outline a sweep line based algorithm to compute this horizontally (or, vertically) convex. Henceforth, except in the partition. Next, we find a coverage motion plan for movement of Section II, unless stated otherwise, the terms 'holed rectilinear the sensor over each rectangle in the partition. Plans for adjacent polygon' and 'polygon' are used interchangeably and both refer rectangles are finally to complete plan for t simple holed rectilinear polygon. merged generate a he to a region.
    [Show full text]
  • CMSC 754 Computational Geometry1
    CMSC 754 Computational Geometry1 David M. Mount Department of Computer Science University of Maryland Spring 2012 1Copyright, David M. Mount, 2012, Dept. of Computer Science, University of Maryland, College Park, MD, 20742. These lecture notes were prepared by David Mount for the course CMSC 754, Computational Geometry, at the University of Maryland. Permission to use, copy, modify, and distribute these notes for educational purposes and withoutfeeisherebygranted,providedthatthiscopyrightnoticeappear in all copies. Lecture Notes 1 CMSC 754 Lecture 1: Introduction to Computational Geometry What is Computational Geometry? “Computational geometry” is a term claimed by a number of different groups. The term was coined perhaps first by Marvin Minsky in his book “Perceptrons”, which was about pattern recognition, and it has also been used often to describe algorithms for manipulating curves and surfaces in solid modeling. Its most widely recognized use, however, is to describe the subfield of algorithm theory that involves the design and analysis of efficient algorithms for problems involving geometric input and output. The field of computational geometry developed rapidly in the late 70’s and through the 80’s and 90’s, and it still continues to develop. Historically, computational geometry developed as a generalization of the study of algorithms for sorting and searching in 1-dimensional spacetoproblemsinvolvingmulti-dimensionalinputs. Because of its history, the field of computational geometry has focused mostly on problems in 2-dimensional space and to a lesser extent in 3-dimensional space. When problems are considered in multi-dimensional spaces, it is usually assumed that the dimension of the space is a smallconstant(say,10orlower).Nonetheless,recent work in this area has considered a limited set of problems in very high dimensional spaces, particularly with respect to approximation algorithms.
    [Show full text]
  • Geometric and Topological Methods in Protein Structure Analysis
    GEOMETRIC AND TOPOLOGICAL METHODS IN PROTEIN STRUCTURE ANALYSIS by Yusu Wang Department of Computer Science Duke University Date: Approved: Prof. Pankaj K. Agarwal, Supervisor Prof. Herbert Edelsbrunner, Co-advisor Prof. John Harer Prof. Johannes Rudolph Dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy in the Department of Computer Science in the Graduate School of Duke University 2004 ABSTRACT GEOMETRIC AND TOPOLOGICAL METHODS IN PROTEIN STRUCTURE ANALYSIS by Yusu Wang Department of Computer Science Duke University Date: Approved: Prof. Pankaj K. Agarwal, Supervisor Prof. Herbert Edelsbrunner, Co-advisor Prof. John Harer Prof. Johannes Rudolph An abstract of a dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy in the Department of Computer Science in the Graduate School of Duke University 2004 Abstract Biology provides some of the most important and complex scientific challenges of our time. With the recent success of the Human Genome Project, one of the main challenges in molecular biology is the determination and exploitation of the three-dimensional structure of proteins and their function. The ability for proteins to perform their numerous functions is made possible by the diversity of their three-dimensional structures, which are capable of highly specific molecular recognition. Hence, to attack the key problems involved, such as protein folding and docking, geometry and topology become important tools. Despite their essential roles, geometric and topological methods are relatively uncommon in com- putational biology, partly due to a number of modeling and algorithmic challenges. This thesis describes efficient computational methods for characterizing and comparing molecu- lar structures by combining both geometric and topological approaches.
    [Show full text]