DOCSLIB.ORG

18.415 Advanced Algorithms Contents

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
18.415 Advanced Algorithms Contents 18.415 Advanced Algorithms Notes from Fall 2020. Last Updated: November 27, 2020. Contents Introduction 6 1 Lecture 1: Fibonacci Heaps7 1.1 MST problem review.................................7 1.2 Using d-heaps for MST................................8 1.3 Introduction to Fibonacci Heaps...........................8 2 Lecture 2: Fibonacci Heaps, Persistent Data Structs 12 2.1 Fibonacci Heaps Continued.............................. 12 2.2 Applications of Fibonacci Heaps........................... 14 2.2.1 Further Improvements............................ 15 2.3 Introduction to Persistent Data Structures...................... 15 3 Lecture 3: Persistent Data Structs, Splay Trees 16 3.1 Persistent Data Structures Continued........................ 16 3.2 The Planar Point Location Problem......................... 17 3.3 Introduction to Splay Trees.............................. 19 4 Lecture 4: Splay Trees 20 4.1 Heuristics of Splay Trees............................... 20 4.2 Solving the Balancing Problem............................ 20 4.3 Implementation and Analysis of Operations..................... 21 4.4 Results with the Access Lemma........................... 23 5 Lecture 5: Splay Updates, Buckets 25 5.1 Wrapping up Splay Trees............................... 25 5.2 Buckets and Indirect Addressing........................... 26 5.2.1 Improvements................................. 27 5.2.2 Formalization with Tries........................... 27 5.2.3 Laziness wins again.............................. 28 1 6 Lecture 6: VEB queues, Hashing 29 6.1 Improvements to the Denardo and Fox queue.................... 29 6.2 VEB queues...................................... 29 6.3 Hashing........................................ 31 7 Lecture 7: Hashing, Max Flows 33 7.1 Hashing with Less Space............................... 33 7.2 Perfect Hash Functions................................ 34 7.3 Combinatorical Optimization............................. 37 7.4 Introduction to the Max Flow Problem........................ 37 8 Lecture 8: Max Flows I 38 8.1 Max Flow Algorithms................................. 41 9 Lecture 9: Max Flows II 43 9.1 Improving on the Augmenting Paths Algorithm................... 43 9.2 Scaling Algorithms.................................. 44 9.3 Strongly Polynomial Algorithms........................... 45 10 Lecture 10: Max Flows III 46 10.1 Edmonds-Karp Algorithm............................... 46 10.2 Blocking Flows.................................... 47 11 Lecture 11: Max Flows IV 50 11.1 Improving Blocking Flows............................... 50 11.2 Min-Cost Max Flows................................. 50 12 Lecture 12: Max Flows V 52 12.1 Price Functions.................................... 52 12.2 Min-Cost Flow Algorithms.............................. 53 13 Lecture 13: Max Flows VI, Linear Programming I 55 13.1 Polynomial Min-cost Flow............................... 55 13.2 Complementary Slackness............................... 55 13.3 Linear Programming.................................. 56 14 Lecture 14: Linear Programming II 58 14.1 Verification and Size of Solutions........................... 58 14.2 Geometry of Solutions................................ 60 2 15 Lecture 15: Linear Programming III 63 15.1 Equivalence of Definitions Continued......................... 63 15.2 Complexity....................................... 64 15.3 Duality......................................... 64 16 Lecture 16: Linear Programming IV 68 16.1 Strong Duality..................................... 68 16.2 Taking a Dual..................................... 69 16.3 Duality - Shortest Path Problem........................... 70 17 Lecture 17: Linear Programming V 72 17.1 Duality - Max Flow Problem............................. 72 17.2 Complementary Slackness............................... 73 17.3 Duality - Min-Cost Circulation............................ 75 18 Lecture 18: Linear Programming VI 76 18.1 More on Basic Feasible Solutions........................... 76 18.2 Simplex Method.................................... 77 18.3 Simplex and Duality.................................. 78 19 Lecture 19: Linear Programming VII 79 19.1 Ellipsoid Method................................... 79 19.2 Interior Point Method................................. 82 20 Lecture 20: Approximation Algorithms I 83 20.1 Introduction to Approximation Algorithms...................... 83 20.2 Greedy Algorithms................................... 85 20.3 Scheduling Theory.................................. 87 21 Lecture 21: Approximation Algorithms II 88 21.1 Scheduling Theory Continued............................. 88 21.2 Approximation Schemes................................ 88 21.2.1 Knapsack Problem Revisited......................... 89 21.2.2 Enumeration Techniques........................... 90 22 Lecture 22: Approximation Algorithms III 91 22.1 Enumeration Techniques Continued......................... 91 22.2 MAX-SNP hard problems............................... 92 22.3 Relaxations...................................... 92 3 23 Lecture 23: Approximation Algorithms IV 94 23.1 Relaxation in Scheduling............................... 94 23.2 General Relaxation with Linear Programming.................... 95 23.2.1 Vertex Cover Problem............................ 95 23.2.2 Facility Location Problem.......................... 96 24 Lecture 24: Approximation Algorithms V, Parameterization 98 24.1 Max-SAT - Relaxation with Rounding........................ 98 24.2 Parametrized Complexity............................... 100 25 Lecture 25: Computational Geometry I 102 25.1 Introduction to Computational Geometry...................... 102 25.2 Orthogonal Range Queries.............................. 102 25.3 Sweep Algorithms................................... 104 25.3.1 Convex Hull Problem............................. 104 25.3.2 Halfspace Intersection Problem....................... 105 26 Lecture 26: Computational Geometry II 106 26.1 Voronoi Diagrams - Introduction........................... 106 26.2 Voronoi Diagrams - Construction........................... 107 27 Lecture 27: Online Algorithms I 110 27.1 Introduction to Online Algorithms.......................... 110 27.2 Ski-Rental....................................... 110 27.3 Selling Stuff...................................... 111 27.4 Online Scheduling................................... 112 27.5 Paging......................................... 112 28 Lecture 28: Online Algorithms II 113 28.1 Paging Continued................................... 113 28.2 Adversarial Inputs................................... 114 28.3 Randomized Paging.................................. 114 29 Lecture 29: Online Algorithms III 116 29.1 A general technique for lower bounds......................... 116 29.2 A lower bound on Paging............................... 117 29.3 The k-server problem................................. 118 4 30 Lecture 30: Online Algs. IV, External Memory Algs. I 119 30.1 Double Coverage Algorithm.............................. 119 30.2 Introduction to External Memory Algorithms.................... 120 31 Lecture 31: External Memory Algorithms II 121 31.1 Matrix Multiplication Continued........................... 121 31.2 Linked Lists...................................... 121 31.3 Search Trees...................................... 122 31.4 Sorting......................................... 123 32 Lecture 32: Parallel Algorithms I 124 32.1 Definitions and Models................................ 124 32.2 Addition........................................ 125 32.3 Parallel Processors/PRAM.............................. 126 33 Lecture 33: Parallel Algorithms II 128 33.1 MAX operation.................................... 128 33.2 Parallel Prefix..................................... 129 33.3 List Ranking...................................... 129 33.4 Binary Search and Sorting.............................. 130 5 Introduction These notes were typeset live from the online 18.415 lectures, taught by David Karger. Remark. Though the course was originally designed as ‘Advanced Algorithms,’ it is probably better to refer to it as ‘Classical Algorithms.’ The course doesn’t go into any cutting-edge algorithms; rather, it provides us a toolkit for algorithms that we are expected to know. We’ll mostly be looking at combinatorical problems, and introducing various models to be able to understand them as well as their efficiency. Most course information can be found at the following link: courses.csail.mit.edu/6.854. The core of the course are long and challenging PSETs, and is complemented by a peer grading assignment and a final project. Collaboration is encouraged and essential, though they should be small groups of size 3. Academic integrity is critical to the course, though in recent years people have always been caught. Due to current conditions, there are many experimental tactics in regards to lectures. Lectures will be recorded, though live lectures will allow for questions. Playing previous lectures may also happen, in where we can stop and ask questions. Self-study / giant office hours during lecture may also be possible. Problem set structure may also be changed, due to lack of facility of collaboration. Collaborators will be changed throughout the semester. There will be sufficient ‘slack points’ for late PSET submissions, but extensions will be granted as well if necessary. 6 1 Lecture 1: Fibonacci Heaps 1.1 MST problem review Fibonacci Heaps were developed by Fredman and Tarjan in 1985, and were done so specifically to solve the Shortest Path/Minimum Spanning Tree problems.
Load more

Recommended publications
  • An Alternative to Fibonacci Heaps with Worst Case Rather Than Amortized Time Bounds∗
    Relaxed Fibonacci heaps: An alternative to Fibonacci heaps with worst case rather than amortized time bounds¤ Chandrasekhar Boyapati C. Pandu Rangan Department of Computer Science and Engineering Indian Institute of Technology, Madras 600036, India Email: [email protected] November 1995 Abstract We present a new data structure called relaxed Fibonacci heaps for implementing priority queues on a RAM. Relaxed Fibonacci heaps support the operations find minimum, insert, decrease key and meld, each in O(1) worst case time and delete and delete min in O(log n) worst case time. Introduction The implementation of priority queues is a classical problem in data structures. Priority queues find applications in a variety of network problems like single source shortest paths, all pairs shortest paths, minimum spanning tree, weighted bipartite matching etc. [1] [2] [3] [4] [5] In the amortized sense, the best performance is achieved by the well known Fibonacci heaps. They support delete and delete min in amortized O(log n) time and find min, insert, decrease key and meld in amortized constant time. Fast meldable priority queues described in [1] achieve all the above time bounds in worst case rather than amortized time, except for the decrease key operation which takes O(log n) worst case time. On the other hand, relaxed heaps described in [2] achieve in the worst case all the time bounds of the Fi- bonacci heaps except for the meld operation, which takes O(log n) worst case ¤Please see Errata at the end of the paper. 1 time. The problem that was posed in [1] was to consider if it is possible to support both decrease key and meld simultaneously in constant worst case time.
    [Show full text]
  • Sweeping the Sphere
    Sweeping the Sphere Joao˜ Dinis Margarida Mamede Departamento de F´ısica CITI, Departamento de Informatica´ Faculdade de Ciencias,ˆ Universidade de Lisboa Faculdade de Cienciasˆ e Tecnologia, FCT Campo Grande, Edif´ıcio C8 Universidade Nova de Lisboa 1749-016 Lisboa, Portugal 2829-516 Caparica, Portugal [email protected] [email protected] Abstract—We introduce the first sweep line algorithm for and Hong [5], [6], which is O(n log n) worst case optimal, computing spherical Voronoi diagrams, which proves that where n is the number of sites. An asymptotically slower Fortune’s method can be extended to points on a sphere alternative in the worst case is the randomized incremental surface. This algorithm is similar to Fortune’s plane sweep algorithm, sweeping the sphere with a circular line instead of algorithm of Clarkson and Shor [7], whose expected running a straight one. time is O(n log n). The well-known Quickhull algorithm of Like its planar counterpart, the novel linear-space algorithm Barber et al. [8] can be seen as an efficient variation of the has worst-case optimal running time. Furthermore, it copes previous algorithm. very well with degeneracies and is easy to implement. Experi- A different approach is to adapt the randomized incremen- mental results show that the performance of our algorithm is very similar to that of Fortune’s algorithm, both with synthetic tal algorithm that computes the planar Delaunay triangula- data sets and with real data. tion [9], [10]. The essential operation used in the incremental The usual solutions make use of the connection between step, which checks if a circle defined by three sites contains a convex hulls and spherical Delaunay triangulations.
    [Show full text]
  • Uwaterloo Latex Thesis Template
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by University of Waterloo's Institutional Repository Approximation Algorithms for Geometric Covering Problems for Disks and Squares by Nan Hu A thesis presented to the University of Waterloo in fulfillment of the thesis requirement for the degree of Master of Mathematics in Computer Science Waterloo, Ontario, Canada, 2013 c Nan Hu 2013 I hereby declare that I am the sole author of this thesis. This is a true copy of the thesis, including any required final revisions, as accepted by my examiners. I understand that my thesis may be made electronically available to the public. ii Abstract Geometric covering is a well-studied topic in computational geometry. We study three covering problems: Disjoint Unit-Disk Cover, Depth-(≤ K) Packing and Red-Blue Unit- Square Cover. In the Disjoint Unit-Disk Cover problem, we are given a point set and want to cover the maximum number of points using disjoint unit disks. We prove that the problem is NP-complete and give a polynomial-time approximation scheme (PTAS) for it. In Depth-(≤ K) Packing for Arbitrary-Size Disks/Squares, we are given a set of arbitrary-size disks/squares, and want to find a subset with depth at most K and maxi- mizing the total area. We prove a depth reduction theorem and present a PTAS. In Red-Blue Unit-Square Cover, we are given a red point set, a blue point set and a set of unit squares, and want to find a subset of unit squares to cover all the blue points and the minimum number of red points.
    [Show full text]
  • Priority Queues and Binary Heaps Chapter 6.5
    Priority Queues and Binary Heaps Chapter 6.5 1 Some animals are more equal than others • A queue is a FIFO data structure • the first element in is the first element out • which of course means the last one in is the last one out • But sometimes we want to sort of have a queue but we want to order items according to some characteristic the item has. 107 - Trees 2 Priorities • We call the ordering characteristic the priority. • When we pull something from this “queue” we always get the element with the best priority (sometimes best means lowest). • It is really common in Operating Systems to use priority to schedule when something happens. e.g. • the most important process should run before a process which isn’t so important • data off disk should be retrieved for more important processes first 107 - Trees 3 Priority Queue • A priority queue always produces the element with the best priority when queried. • You can do this in many ways • keep the list sorted • or search the list for the minimum value (if like the textbook - and Unix actually - you take the smallest value to be the best) • You should be able to estimate the Big O values for implementations like this. e.g. O(n) for choosing the minimum value of an unsorted list. • There is a clever data structure which allows all operations on a priority queue to be done in O(log n). 107 - Trees 4 Binary Heap Actually binary min heap • Shape property - a complete binary tree - all levels except the last full.
    [Show full text]
  • Assignment 3: Kdtree ______Due June 4, 11:59 PM
    CS106L Handout #04 Spring 2014 May 15, 2014 Assignment 3: KDTree _________________________________________________________________________________________________________ Due June 4, 11:59 PM Over the past seven weeks, we've explored a wide array of STL container classes. You've seen the linear vector and deque, along with the associative map and set. One property common to all these containers is that they are exact. An element is either in a set or it isn't. A value either ap- pears at a particular position in a vector or it does not. For most applications, this is exactly what we want. However, in some cases we may be interested not in the question “is X in this container,” but rather “what value in the container is X most similar to?” Queries of this sort often arise in data mining, machine learning, and computational geometry. In this assignment, you will implement a special data structure called a kd-tree (short for “k-dimensional tree”) that efficiently supports this operation. At a high level, a kd-tree is a generalization of a binary search tree that stores points in k-dimen- sional space. That is, you could use a kd-tree to store a collection of points in the Cartesian plane, in three-dimensional space, etc. You could also use a kd-tree to store biometric data, for example, by representing the data as an ordered tuple, perhaps (height, weight, blood pressure, cholesterol). However, a kd-tree cannot be used to store collections of other data types, such as strings. Also note that while it's possible to build a kd-tree to hold data of any dimension, all of the data stored in a kd-tree must have the same dimension.
    [Show full text]
  • Advanced Data Structures
    Advanced Data Structures PETER BRASS City College of New York CAMBRIDGE UNIVERSITY PRESS Cambridge, New York, Melbourne, Madrid, Cape Town, Singapore, São Paulo Cambridge University Press The Edinburgh Building, Cambridge CB2 8RU, UK Published in the United States of America by Cambridge University Press, New York www.cambridge.org Information on this title: www.cambridge.org/9780521880374 © Peter Brass 2008 This publication is in copyright. Subject to statutory exception and to the provision of relevant collective licensing agreements, no reproduction of any part may take place without the written permission of Cambridge University Press. First published in print format 2008 ISBN-13 978-0-511-43685-7 eBook (EBL) ISBN-13 978-0-521-88037-4 hardback Cambridge University Press has no responsibility for the persistence or accuracy of urls for external or third-party internet websites referred to in this publication, and does not guarantee that any content on such websites is, or will remain, accurate or appropriate. Contents Preface page xi 1 Elementary Structures 1 1.1 Stack 1 1.2 Queue 8 1.3 Double-Ended Queue 16 1.4 Dynamical Allocation of Nodes 16 1.5 Shadow Copies of Array-Based Structures 18 2 Search Trees 23 2.1 Two Models of Search Trees 23 2.2 General Properties and Transformations 26 2.3 Height of a Search Tree 29 2.4 Basic Find, Insert, and Delete 31 2.5ReturningfromLeaftoRoot35 2.6 Dealing with Nonunique Keys 37 2.7 Queries for the Keys in an Interval 38 2.8 Building Optimal Search Trees 40 2.9 Converting Trees into Lists 47 2.10
    [Show full text]
  • Rethinking Host Network Stack Architecture Using a Dataflow Modeling Approach
    DISS.ETH NO. 23474 Rethinking host network stack architecture using a dataflow modeling approach A thesis submitted to attain the degree of DOCTOR OF SCIENCES of ETH ZURICH (Dr. sc. ETH Zurich) presented by Pravin Shinde Master of Science, Vrije Universiteit, Amsterdam born on 15.10.1982 citizen of Republic of India accepted on the recommendation of Prof. Dr. Timothy Roscoe, examiner Prof. Dr. Gustavo Alonso, co-examiner Dr. Kornilios Kourtis, co-examiner Dr. Andrew Moore, co-examiner 2016 Abstract As the gap between the speed of networks and processor cores increases, the software alone will not be able to handle all incoming data without additional assistance from the hardware. The network interface controllers (NICs) evolve and add supporting features which could help the system increase its scalability with respect to incoming packets, provide Quality of Service (QoS) guarantees and reduce the CPU load. However, modern operating systems are ill suited to both efficiently exploit and effectively manage the hardware resources of state-of-the-art NICs. The main problem is the layered architecture of the network stack and the rigid interfaces. This dissertation argues that in order to effectively use the diverse and complex NIC hardware features, we need (i) a hardware agnostic representation of the packet processing capabilities of the NICs, and (ii) a flexible interface to share this information with different layers of the network stack. This work presents the Dataflow graph based model to capture both the hardware capabilities for packet processing of the NIC and the state of the network stack, in order to enable automated reasoning about the NIC features in a hardware-agnostic way.
    [Show full text]
  • Priorityqueue
    CSE 373 Java Collection Framework, Part 2: Priority Queue, Map slides created by Marty Stepp http://www.cs.washington.edu/373/ © University of Washington, all rights reserved. 1 Priority queue ADT • priority queue : a collection of ordered elements that provides fast access to the minimum (or maximum) element usually implemented using a tree structure called a heap • priority queue operations: add adds in order; O(log N) worst peek returns minimum value; O(1) always remove removes/returns minimum value; O(log N) worst isEmpty , clear , size , iterator O(1) always 2 Java's PriorityQueue class public class PriorityQueue< E> implements Queue< E> Method/Constructor Description Runtime PriorityQueue< E>() constructs new empty queue O(1) add( E value) adds value in sorted order O(log N ) clear() removes all elements O(1) iterator() returns iterator over elements O(1) peek() returns minimum element O(1) remove() removes/returns min element O(log N ) Queue<String> pq = new PriorityQueue <String>(); pq.add("Stuart"); pq.add("Marty"); ... 3 Priority queue ordering • For a priority queue to work, elements must have an ordering in Java, this means implementing the Comparable interface • many existing types (Integer, String, etc.) already implement this • if you store objects of your own types in a PQ, you must implement it TreeSet and TreeMap also require Comparable types public class Foo implements Comparable<Foo> { … public int compareTo(Foo other) { // Return > 0 if this object is > other // Return < 0 if this object is < other // Return 0 if this object == other } } 4 The Map ADT • map : Holds a set of unique keys and a collection of values , where each key is associated with one value.
    [Show full text]
  • Programmatic Testing of the Standard Template Library Containers
    Programmatic Testing of the Standard Template Library Containers y z Jason McDonald Daniel Ho man Paul Stro op er May 11, 1998 Abstract In 1968, McIlroy prop osed a software industry based on reusable comp onents, serv- ing roughly the same role that chips do in the hardware industry. After 30 years, McIlroy's vision is b ecoming a reality. In particular, the C++ Standard Template Library STL is an ANSI standard and is b eing shipp ed with C++ compilers. While considerable attention has b een given to techniques for developing comp onents, little is known ab out testing these comp onents. This pap er describ es an STL conformance test suite currently under development. Test suites for all of the STL containers have b een written, demonstrating the feasi- bility of thorough and highly automated testing of industrial comp onent libraries. We describ e a ordable test suites that provide go o d co de and b oundary value coverage, including the thousands of cases that naturally o ccur from combinations of b oundary values. We showhowtwo simple oracles can provide fully automated output checking for all the containers. We re ne the traditional categories of black-b ox and white-b ox testing to sp eci cation-based, implementation-based and implementation-dep endent testing, and showhow these three categories highlight the key cost/thoroughness trade- o s. 1 Intro duction Our testing fo cuses on container classes |those providing sets, queues, trees, etc.|rather than on graphical user interface classes. Our approach is based on programmatic testing where the number of inputs is typically very large and b oth the input generation and output checking are under program control.
    [Show full text]
  • Visibility Graphs and Cell Decompositions
    Visibility Graphs and Cell Decompositions CIS 390 Kostas Daniilidis With material from Chapter 5 - Roadmaps Principles of Robot Motion: Theory, Algorithms, and Implementation by Howie ChosetÂet al. The MIT Press © 2005 For polygonal obstacles in 2D • Assume robot is a point • Any shortest path from start to goal among a set of disjoint polygonal obstacles is a polygonal path whose inner vertices are convex vertices of the obstacles (imagine a tight rope from start to end) Visibility graph • Vertices: all vertices of the polygonal obstacles plus the start and the goal • Edges: all line segments between vertices that do not intersect obstacles • It is not a planar graph: edges are crossing (not at vertices) Visibility graph construction • Brute force O(n^3) algorithm visits – all n vertices – applies a rotational plane sweep that connects with all other n vertices – and determines whether each segment intersects any of the O(n) edges • We can do better by sorting the vertices. Sweep Line Algorithm • Input: A set of vertices {νi} (whose edges do not intersect) and a vertex ν • Output: A subset of vertices from {νi} that are within line of sight of ν • 1: For each vertex vi, calculate αi, the angle from the horizontal axis to the line segment • ννi. • 2: Create the vertex list E , containing the αi 's sorted in increasing order. • 3: Create the active list S, containing the sorted list of edges that intersect the horizontal • half-line emanating from ν. • 4: for all αi do • 5: if νi is visible to ν then • 6: Add the edge (ν, νi )to the visibility graph.
    [Show full text]
  • Introduction to Algorithms and Data Structures
    Introduction to Algorithms and Data Structures Markus Bläser Saarland University Draft—Thursday 22, 2015 and forever Contents 1 Introduction 1 1.1 Binary search . .1 1.2 Machine model . .3 1.3 Asymptotic growth of functions . .5 1.4 Running time analysis . .7 1.4.1 On foot . .7 1.4.2 By solving recurrences . .8 2 Sorting 11 2.1 Selection-sort . 11 2.2 Merge sort . 13 3 More sorting procedures 16 3.1 Heap sort . 16 3.1.1 Heaps . 16 3.1.2 Establishing the Heap property . 18 3.1.3 Building a heap from scratch . 19 3.1.4 Heap sort . 20 3.2 Quick sort . 21 4 Selection problems 23 4.1 Lower bounds . 23 4.1.1 Sorting . 25 4.1.2 Minimum selection . 27 4.2 Upper bounds for selecting the median . 27 5 Elementary data structures 30 5.1 Stacks . 30 5.2 Queues . 31 5.3 Linked lists . 33 6 Binary search trees 36 6.1 Searching . 38 6.2 Minimum and maximum . 39 6.3 Successor and predecessor . 39 6.4 Insertion and deletion . 40 i ii CONTENTS 7 AVL trees 44 7.1 Bounds on the height . 45 7.2 Restoring the AVL tree property . 46 7.2.1 Rotations . 46 7.2.2 Insertion . 46 7.2.3 Deletion . 49 8 Binomial Heaps 52 8.1 Binomial trees . 52 8.2 Binomial heaps . 54 8.3 Operations . 55 8.3.1 Make heap . 55 8.3.2 Minimum . 55 8.3.3 Union . 56 8.3.4 Insert .
    [Show full text]
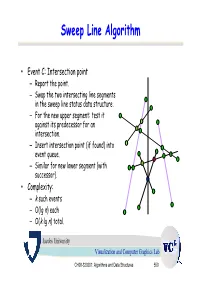
  • Sweep Line Algorithm
    Sweep Line Algorithm • Event C: Intersection point – Report the point. – Swap the two intersecting line segments in the sweep line status data structure. – For the new upper segment: test it against its predecessor for an intersection. – Insert intersection point (if found) into event queue. – Similar for new lower segment (with successor). • Complexity: – k such events – O(lg n) each – O(k lg n) total. Jacobs University Visualization and Computer Graphics Lab CH08-320201: Algorithms and Data Structures 550 Example a3 b4 Sweep Line status: s3 e1 s4 s0, s1, s2, s3 Event Queue: a2 a4 b3 a4, b1, b2, b0, b3, b4 s2 b1 b0 s1 b2 s0 a1 a0 Jacobs University Visualization and Computer Graphics Lab CH08-320201: Algorithms and Data Structures 551 Example a3 b4 Actions: s3 Insert s4 to SLS e1 s4 Test s4-s3 and s4-s2. a2 a4 b3 Add e1 to EQ s2 b1 Sweep Line status: b0 s1 b2 s0, s1, s2, s4, s3 s0 a1 a0 Event Queue: b1, e1, b2, b0, b3, b4 Jacobs University Visualization and Computer Graphics Lab CH08-320201: Algorithms and Data Structures 552 Example a3 b4 Actions: s3 e1 s4 Delete s1 from SLS Test s0-s2. a2 a4 b3 Add e2 to EQ s2 Sweep Line status: e2 b0 b1 s1 b2 s0, s2, s4, s3 s0 a1 a0 Event Queue: e1, e2, b2, b0, b3, b4 Jacobs University Visualization and Computer Graphics Lab CH08-320201: Algorithms and Data Structures 553 Example a3 b4 Actions: s3 e1 s4 Swap s3 and s4 in SLS Test s3-s2.
    [Show full text]