CMSC 754 Computational Geometry1
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Object Oriented Programming
No. 52 March-A pril'1990 $3.95 T H E M TEe H CAL J 0 URN A L COPIA Object Oriented Programming First it was BASIC, then it was structures, now it's objects. C++ afi<;ionados feel, of course, that objects are so powerful, so encompassing that anything could be so defined. I hope they're not placing bets, because if they are, money's no object. C++ 2.0 page 8 An objective view of the newest C++. Training A Neural Network Now that you have a neural network what do you do with it? Part two of a fascinating series. Debugging C page 21 Pointers Using MEM Keep C fro111 (C)rashing your system. An AT Keyboard Interface Use an AT keyboard with your latest project. And More ... Understanding Logic Families EPROM Programming Speeding Up Your AT Keyboard ((CHAOS MADE TO ORDER~ Explore the Magnificent and Infinite World of Fractals with FRAC LS™ AN ELECTRONIC KALEIDOSCOPE OF NATURES GEOMETRYTM With FracTools, you can modify and play with any of the included images, or easily create new ones by marking a region in an existing image or entering the coordinates directly. Filter out areas of the display, change colors in any area, and animate the fractal to create gorgeous and mesmerizing images. Special effects include Strobe, Kaleidoscope, Stained Glass, Horizontal, Vertical and Diagonal Panning, and Mouse Movies. The most spectacular application is the creation of self-running Slide Shows. Include any PCX file from any of the popular "paint" programs. FracTools also includes a Slide Show Programming Language, to bring a higher degree of control to your shows. -

A Computational Basis for Conic Arcs and Boolean Operations on Conic Polygons
A Computational Basis for Conic Arcs and Boolean Operations on Conic Polygons Eric Berberich, Arno Eigenwillig, Michael Hemmer Susan Hert, Kurt Mehlhorn, and Elmar Schomer¨ [eric|arno|hemmer|hert|mehlhorn|schoemer]@mpi-sb.mpg.de Max-Planck-Institut fur¨ Informatik, Stuhlsatzenhausweg 85 66123 Saarbruck¨ en, Germany Abstract. We give an exact geometry kernel for conic arcs, algorithms for ex- act computation with low-degree algebraic numbers, and an algorithm for com- puting the arrangement of conic arcs that immediately leads to a realization of regularized boolean operations on conic polygons. A conic polygon, or polygon for short, is anything that can be obtained from linear or conic halfspaces (= the set of points where a linear or quadratic function is non-negative) by regularized boolean operations. The algorithm and its implementation are complete (they can handle all cases), exact (they give the mathematically correct result), and efficient (they can handle inputs with several hundred primitives). 1 Introduction We give an exact geometry kernel for conic arcs, algorithms for exact computation with low-degree algebraic numbers, and a sweep-line algorithm for computing arrangements of curved arcs that immediately leads to a realization of regularized boolean operations on conic polygons. A conic polygon, or polygon for short, is anything that can be ob- tained from linear or conic halfspaces (= the set of points where a linear or quadratic function is non-negative) by regularized boolean operations (Figure 1). A regularized boolean operation is a standard boolean operation (union, intersection, complement) followed by regularization. Regularization replaces a set by the closure of its interior and eliminates dangling low-dimensional features. -

Sweeping the Sphere
Sweeping the Sphere Joao˜ Dinis Margarida Mamede Departamento de F´ısica CITI, Departamento de Informatica´ Faculdade de Ciencias,ˆ Universidade de Lisboa Faculdade de Cienciasˆ e Tecnologia, FCT Campo Grande, Edif´ıcio C8 Universidade Nova de Lisboa 1749-016 Lisboa, Portugal 2829-516 Caparica, Portugal [email protected] [email protected] Abstract—We introduce the first sweep line algorithm for and Hong [5], [6], which is O(n log n) worst case optimal, computing spherical Voronoi diagrams, which proves that where n is the number of sites. An asymptotically slower Fortune’s method can be extended to points on a sphere alternative in the worst case is the randomized incremental surface. This algorithm is similar to Fortune’s plane sweep algorithm, sweeping the sphere with a circular line instead of algorithm of Clarkson and Shor [7], whose expected running a straight one. time is O(n log n). The well-known Quickhull algorithm of Like its planar counterpart, the novel linear-space algorithm Barber et al. [8] can be seen as an efficient variation of the has worst-case optimal running time. Furthermore, it copes previous algorithm. very well with degeneracies and is easy to implement. Experi- A different approach is to adapt the randomized incremen- mental results show that the performance of our algorithm is very similar to that of Fortune’s algorithm, both with synthetic tal algorithm that computes the planar Delaunay triangula- data sets and with real data. tion [9], [10]. The essential operation used in the incremental The usual solutions make use of the connection between step, which checks if a circle defined by three sites contains a convex hulls and spherical Delaunay triangulations. -

Uwaterloo Latex Thesis Template
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by University of Waterloo's Institutional Repository Approximation Algorithms for Geometric Covering Problems for Disks and Squares by Nan Hu A thesis presented to the University of Waterloo in fulfillment of the thesis requirement for the degree of Master of Mathematics in Computer Science Waterloo, Ontario, Canada, 2013 c Nan Hu 2013 I hereby declare that I am the sole author of this thesis. This is a true copy of the thesis, including any required final revisions, as accepted by my examiners. I understand that my thesis may be made electronically available to the public. ii Abstract Geometric covering is a well-studied topic in computational geometry. We study three covering problems: Disjoint Unit-Disk Cover, Depth-(≤ K) Packing and Red-Blue Unit- Square Cover. In the Disjoint Unit-Disk Cover problem, we are given a point set and want to cover the maximum number of points using disjoint unit disks. We prove that the problem is NP-complete and give a polynomial-time approximation scheme (PTAS) for it. In Depth-(≤ K) Packing for Arbitrary-Size Disks/Squares, we are given a set of arbitrary-size disks/squares, and want to find a subset with depth at most K and maxi- mizing the total area. We prove a depth reduction theorem and present a PTAS. In Red-Blue Unit-Square Cover, we are given a red point set, a blue point set and a set of unit squares, and want to find a subset of unit squares to cover all the blue points and the minimum number of red points. -

On Combinatorial Approximation Algorithms in Geometry Bruno Jartoux
On combinatorial approximation algorithms in geometry Bruno Jartoux To cite this version: Bruno Jartoux. On combinatorial approximation algorithms in geometry. Distributed, Parallel, and Cluster Computing [cs.DC]. Université Paris-Est, 2018. English. NNT : 2018PESC1078. tel- 02066140 HAL Id: tel-02066140 https://pastel.archives-ouvertes.fr/tel-02066140 Submitted on 13 Mar 2019 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Université Paris-Est École doctorale MSTIC On Combinatorial Sur les algorithmes d’approximation Approximation combinatoires Algorithms en géométrie in Geometry Bruno Jartoux Thèse de doctorat en informatique soutenue le 12 septembre 2018. Composition du jury : Lilian Buzer ESIEE Paris Jean Cardinal Université libre de Bruxelles président du jury Guilherme Dias da Fonseca Université Clermont Auvergne rapporteur Jesús A. de Loera University of California, Davis rapporteur Frédéric Meunier École nationale des ponts et chaussées Nabil H. Mustafa ESIEE Paris directeur Vera Sacristán Universitat Politècnica de Catalunya Kasturi R. Varadarajan The University of Iowa rapporteur Last revised 16th December 2018. Thèse préparée au laboratoire d’informatique Gaspard-Monge (LIGM), équipe A3SI, dans les locaux d’ESIEE Paris. LIGM UMR 8049 ESIEE Paris Cité Descartes, bâtiment Copernic Département IT 5, boulevard Descartes Cité Descartes Champs-sur-Marne 2, boulevard Blaise-Pascal 77454 Marne-la-Vallée Cedex 2 93162 Noisy-le-Grand Cedex Bruno Jartoux 2018. -

2020 SIGACT REPORT SIGACT EC – Eric Allender, Shuchi Chawla, Nicole Immorlica, Samir Khuller (Chair), Bobby Kleinberg September 14Th, 2020
2020 SIGACT REPORT SIGACT EC – Eric Allender, Shuchi Chawla, Nicole Immorlica, Samir Khuller (chair), Bobby Kleinberg September 14th, 2020 SIGACT Mission Statement: The primary mission of ACM SIGACT (Association for Computing Machinery Special Interest Group on Algorithms and Computation Theory) is to foster and promote the discovery and dissemination of high quality research in the domain of theoretical computer science. The field of theoretical computer science is the rigorous study of all computational phenomena - natural, artificial or man-made. This includes the diverse areas of algorithms, data structures, complexity theory, distributed computation, parallel computation, VLSI, machine learning, computational biology, computational geometry, information theory, cryptography, quantum computation, computational number theory and algebra, program semantics and verification, automata theory, and the study of randomness. Work in this field is often distinguished by its emphasis on mathematical technique and rigor. 1. Awards ▪ 2020 Gödel Prize: This was awarded to Robin A. Moser and Gábor Tardos for their paper “A constructive proof of the general Lovász Local Lemma”, Journal of the ACM, Vol 57 (2), 2010. The Lovász Local Lemma (LLL) is a fundamental tool of the probabilistic method. It enables one to show the existence of certain objects even though they occur with exponentially small probability. The original proof was not algorithmic, and subsequent algorithmic versions had significant losses in parameters. This paper provides a simple, powerful algorithmic paradigm that converts almost all known applications of the LLL into randomized algorithms matching the bounds of the existence proof. The paper further gives a derandomized algorithm, a parallel algorithm, and an extension to the “lopsided” LLL. -

Visibility Graphs and Cell Decompositions
Visibility Graphs and Cell Decompositions CIS 390 Kostas Daniilidis With material from Chapter 5 - Roadmaps Principles of Robot Motion: Theory, Algorithms, and Implementation by Howie ChosetÂet al. The MIT Press © 2005 For polygonal obstacles in 2D • Assume robot is a point • Any shortest path from start to goal among a set of disjoint polygonal obstacles is a polygonal path whose inner vertices are convex vertices of the obstacles (imagine a tight rope from start to end) Visibility graph • Vertices: all vertices of the polygonal obstacles plus the start and the goal • Edges: all line segments between vertices that do not intersect obstacles • It is not a planar graph: edges are crossing (not at vertices) Visibility graph construction • Brute force O(n^3) algorithm visits – all n vertices – applies a rotational plane sweep that connects with all other n vertices – and determines whether each segment intersects any of the O(n) edges • We can do better by sorting the vertices. Sweep Line Algorithm • Input: A set of vertices {νi} (whose edges do not intersect) and a vertex ν • Output: A subset of vertices from {νi} that are within line of sight of ν • 1: For each vertex vi, calculate αi, the angle from the horizontal axis to the line segment • ννi. • 2: Create the vertex list E , containing the αi 's sorted in increasing order. • 3: Create the active list S, containing the sorted list of edges that intersect the horizontal • half-line emanating from ν. • 4: for all αi do • 5: if νi is visible to ν then • 6: Add the edge (ν, νi )to the visibility graph. -

Mathematics of Bioinformatics ---Theory, Practice, and Applications (Part I)
Mathematics of Bioinformatics ---Theory, Practice, and Applications (Part I) Matthew He, Ph.D. Professor/Director Division of Math, Science, and Technology Nova Southeastern University, Florida, USA December 18-21, 2010, Hong Kong, China BIBM 2010 OUTLINE INTRODUCTION: FUNDAMENTAL QUESTIONS PART I : GENETIC CODES , BIOLOGICAL SEQUENCES , DNA AND PROTEIN STRUCTURES PART II: BIOLOGICAL FUNCTIONS, NETWORKS, SYSTEMS BIOLOGY AND COGNITIVE INFORMATICS TABLE OF TOPICS: PART I I. Bioinformatics and Mathematics 1.1 Introduction 12G1.2 Genet ic Co de an dMd Mat hemat ics 1.3 Mathematical Background 1.4 Converting Data to Knowledge 1.5 Big Picture: Informatics 16Chll1.6 Challenges and dP Perspect ives II. Genetic Codes, Matrices, and Symmetrical Techniques 2.1 Introduction 2.2 Matrix Theory and Symmetry Preliminaries 2.3 Genetic Codes and Matrices 2.4 Challenges and Perspectives III. Biological Sequences, Sequence Alignment, and Statistics 3.1 Introduction 3.2 Mathematical Sequences 3.3 Sequence Alignment 3.4 Sequence Analysis/Further Discussions 3.5 Challenges and Perspectives TABLE OF TOPICS: PART I IV. Structures of DNA and Knot Theory 4.1 Introduction 4.2 Knot Theory Preliminaries 4.3 DNA Knots and Links 4.4 Challenggpes and Perspectives V. Protein Structures, Geometry, and Topology 51I5.1 In tro duc tion 5.2 Computational Geometry and Topology 5.3 Protein Structures and Prediction 5.4 Statistical Approach and Discussions 5. 5 Cha llenges an d Perspec tives TABLE OF TOPICS: PART II VI. Biological Networks and Graph Theory 6. 1 Introduction 6.2 Graph Theory and Network Topology 6.3 Models of Biological Networks 6.4 Challenges and Perspectives VII. -
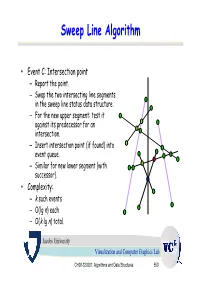
Sweep Line Algorithm
Sweep Line Algorithm • Event C: Intersection point – Report the point. – Swap the two intersecting line segments in the sweep line status data structure. – For the new upper segment: test it against its predecessor for an intersection. – Insert intersection point (if found) into event queue. – Similar for new lower segment (with successor). • Complexity: – k such events – O(lg n) each – O(k lg n) total. Jacobs University Visualization and Computer Graphics Lab CH08-320201: Algorithms and Data Structures 550 Example a3 b4 Sweep Line status: s3 e1 s4 s0, s1, s2, s3 Event Queue: a2 a4 b3 a4, b1, b2, b0, b3, b4 s2 b1 b0 s1 b2 s0 a1 a0 Jacobs University Visualization and Computer Graphics Lab CH08-320201: Algorithms and Data Structures 551 Example a3 b4 Actions: s3 Insert s4 to SLS e1 s4 Test s4-s3 and s4-s2. a2 a4 b3 Add e1 to EQ s2 b1 Sweep Line status: b0 s1 b2 s0, s1, s2, s4, s3 s0 a1 a0 Event Queue: b1, e1, b2, b0, b3, b4 Jacobs University Visualization and Computer Graphics Lab CH08-320201: Algorithms and Data Structures 552 Example a3 b4 Actions: s3 e1 s4 Delete s1 from SLS Test s0-s2. a2 a4 b3 Add e2 to EQ s2 Sweep Line status: e2 b0 b1 s1 b2 s0, s2, s4, s3 s0 a1 a0 Event Queue: e1, e2, b2, b0, b3, b4 Jacobs University Visualization and Computer Graphics Lab CH08-320201: Algorithms and Data Structures 553 Example a3 b4 Actions: s3 e1 s4 Swap s3 and s4 in SLS Test s3-s2. -

Parallel Range, Segment and Rectangle Queries with Augmented Maps
Parallel Range, Segment and Rectangle Queries with Augmented Maps Yihan Sun Guy E. Blelloch Carnegie Mellon University Carnegie Mellon University [email protected] [email protected] Abstract The range, segment and rectangle query problems are fundamental problems in computational geometry, and have extensive applications in many domains. Despite the significant theoretical work on these problems, efficient implementations can be complicated. We know of very few practical implementations of the algorithms in parallel, and most implementations do not have tight theoretical bounds. In this paper, we focus on simple and efficient parallel algorithms and implementations for range, segment and rectangle queries, which have tight worst-case bound in theory and good parallel performance in practice. We propose to use a simple framework (the augmented map) to model the problem. Based on the augmented map interface, we develop both multi-level tree structures and sweepline algorithms supporting range, segment and rectangle queries in two dimensions. For the sweepline algorithms, we also propose a parallel paradigm and show corresponding cost bounds. All of our data structures are work-efficient to build in theory (O(n log n) sequential work) and achieve a low parallel depth (polylogarithmic for the multi-level tree structures, and O(n) for sweepline algorithms). The query time is almost linear to the output size. We have implemented all the data structures described in the paper using a parallel augmented map library. Based on the library each data structure only requires about 100 lines of C++ code. We test their performance on large data sets (up to 108 elements) and a machine with 72-cores (144 hyperthreads). -

Computational Geometry and Computer Graphics by Dobkin
Computational Geometry and Computer Graphics David P. Dobkin+ Department of Computer Science Princeton University Princeton, NJ 08544 ABSTRACT Computer graphics is a de®ning application for computational geometry. The interaction between these ®elds is explored through two scenarios. Spatial subdivisions studied from the viewpoint of computa- tional geometry are shown to have found application in computer graph- ics. Hidden surface removal problems of computer graphics have led to sweepline and area subdivision algorithms in computational geometry. The paper ends with two promising research areas with practical applica- tions: precise computation and polyhedral decomposition. 1. Introduction Computational geometry and computer graphics both consider geometric phenomena as they relate to computing. Computational geometry provides a theoretical foundation involving the study of algorithms and data structures for doing geometric computations. Computer graphics concerns the practical development of the software, hardware and algorithms necessary to create graphics (i.e. to display geometry) on the computer screen. At the interface lie many common problems which each discipline must solve to reach its goal. The techniques of the ®eld are often similar, sometimes dif- ferent. And, each ®elds has built a set of paradigms from which to operate. Thus, it is natural to ask the question: How do computer graphics and computational geometry interact? It is this question that motivates this paper. I explore here life at the interface between computational geometry and computer graphics. Rather than striving for completeness (see e.g. Yao [Ya] for a broader survey), I consider in detail two scenarios in which the two ®elds have overlapped. The goal is to trace the development of the ideas used in the two areas and to document the movement back and forth. -

Variations of Enclosing Problem Using Axis Parallel Square(S): a General Approach
American Journal of Computational Mathematics, 2014, 4, 197-205 Published Online June 2014 in SciRes. http://www.scirp.org/journal/ajcm http://dx.doi.org/10.4236/ajcm.2014.43016 Variations of Enclosing Problem Using Axis Parallel Square(s): A General Approach Priya Ranjan Sinha Mahapatra Department of Computer Science and Engineering, University of Kalyani, Kalyani, India Email: [email protected] Received 16 December 2013; revised 6 January 2014; accepted 15 January 2014 Copyright © 2014 by author and Scientific Research Publishing Inc. This work is licensed under the Creative Commons Attribution International License (CC BY). http://creativecommons.org/licenses/by/4.0/ Abstract Let P be a set of n points in two dimensional plane. For each point pP∈ , we locate an axis- parallel unit square having one particular side passing through p and enclosing the maximum number of points from P . Considering all points pP∈ , such n squares can be reported in On( log n) time. We show that this result can be used to (i) locate m (> 2) axis-parallel unit squares which are pairwise disjoint and they together enclose the maximum number of points from P (if exists) and (ii) find the smallest axis-parallel square enclosing at least k points of P , 2 ≤≤kn. Keywords Axis-Parallel Unit Square, Sweep Line Algorithm, Maximium Enclosing Problem, K-Enclosing Problem 1. Introduction Given a set P= { pp12,,, pn } points in a plane, enclosing problem in computational geometry is concerned with finding the smallest geometrical object of a given type that encloses all the points of P . Some well known instances of the enclosing problem are finding minimum enclosing circle [1], minimum area triangle [2], minimum area rectangle [3], minimum bounding box [4], and smallest width annulus [5].