DOCSLIB.ORG

COST 327 Motorcycle Safety Helmets Final Report

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
COST 327 Motorcycle Safety Helmets Final Report European Co-operation in the Field of Scientific and Technical Research COST 327 Motorcycle Safety Helmets Final Report of the Action European Commission Directorate General for Energy and Transport Legal notice Neither the European Commission nor any person acting on behalf of the Commission is responsible for the use, which might be made of the following information. The views expressed in this publication do not necessarily reflect the views of the European Commission. A great deal of additional information on COST Transport is available on the World Wide Web. It can be accessed through the CORDIS server at the following address: http://www.cordis.lu/cost-transport/home.html Cataloguing data can be found at the end of this publication. Luxembourg: Office for Official Publications of the European Communities, 2001. ISBN xx-xxx-xxxx-x © European Communities 2001 Printed in Belgium Key Authors: Bryan CHINN, TRL Limited, U.K. Bertrand CANAPLE, University of Valenciennes Siegfried DERLER, EMPA, Switzerland David DOYLE, Southern General Hospital, Glasgow. Dietmar OTTE, University of Hannover Erich SCHULLER, University of Munich Remy WILLINGER, University of Louis Pasteur, Strasbourg The COST 327 Management Committee, together with the Chairman, Steve Gillingham, would like to thank all the members of the Action, in particular the authors of this report and earlier publications, for their valued contributions without which the success of this research would not have been possible. In addition, the Committee would like to acknowledge the support provided by Andrew Stimpson, Martin Kemp and René Bastiaans of the European Commission, and the kind assistance of Mary Legg, who compiled the report. Editor-in-Chief: Dr Bryan Chinn United Kingdom Department for Transport, (DfT) Zone 2/06 Great Minster House, 76 Marsham Street, London SW1P 4DR. +44 20 7944 3000. www.dft.gov.uk Southern General Hospital, Department of Neuropathology, 1345 Govan Road, Glasgow G51 4TF. +44 141 201 1100. www.show.scot.nhs.uk TRL Limited, Old Wokingham Road, Crowthorne, Berkshire, RG45 6AU. +44 1344 773131.www.trl.co.uk France INRETS Case 24, F69675, Bron Cedex. +33(0)1 47 407000 www.inrets.fr Institut de Mecanique des Fluides Laboratoire de Biomecanique, Rue Boussingault, 2, F-67083 Strasbourg Cedex. +33 3 88 41 65 65. www.intelus.u-strasbg.fr Laboratoire de Genie Mecanique Le Mont Houy, BP 311, 59304 Valenciennes. +33 3 27 51 12 34. www.univ-valenciennes.fr Germany Accident Research Unit, University of Hannover, Carl-Neuberg- Strasse 1, 30625 Hannover. +49 0511 532-0. www.mh-hannover.de Institut fűr Rechtsmedizin, Ludwig-Maximilians-Universität, Frauenlobstrasse 7a, D-80337 München. +49 89 5160 5111. www.lmu.de Hungary AUTOKUT, PF 25, XI Csoka u.9, H-1502 Budapest. Italy AGV spa Zona Industriale D5, I-15047 Spinetta (Alessandrio). +39 01 31 213211 Dipartimento di Ingeneria Aerospatialle, Politecnico di Milano Via Lambrushchini 15, Milano. +39 02 23991. www.polimi.it Netherlands Technische Universiteit Eindhoven, Department of Biomedical Engineering, Den Dolech 2, 5600 MB Eindhoven. +31 40 247 9111. www.tue.nl Sweden Götenburg University, SE 40530 Götenburg. +46 31773 1004. www.gu.se Switzerland EMPA, Lerchenfeldstrasse 5, CH-9014 St. Gallen. +41 71 274 74 74. www.empa.ch Table of Contents Table of Contents EXECUTIVE SUMMARY....................................................................................................i CHAPTER 1. INTRODUCTION.........................................................................................1 CHAPTER 2. LITERATURE REVIEW..............................................................................5 2.1. Introduction...............................................................................................................5 2.2. Accidents and injury mechanisms.............................................................................5 2.2.1. References.........................................................................................................6 2.3. Biomechanics of head injury.....................................................................................6 2.3.1. References.........................................................................................................7 2.4. Mathematical modelling of the human head and neck..............................................8 2.4.1. References.........................................................................................................9 2.5. Motorcycle helmets: performance and current Standards.........................................9 2.5.1. References.......................................................................................................10 CHAPTER 3. ACCIDENT INVESTIGATION.................................................................11 3.1. Introduction.............................................................................................................11 3.2. Description of the COST 327 database...................................................................11 3.3. Accident sampling areas .........................................................................................12 3.3.1. Accident Research Unit - Medical University Hannover / Germany .............12 3.3.2. Department of Neuropathology, Glasgow/UK ...............................................13 3.3.3. Institute for Legal Medicine, Munich University / Germany .........................14 3.3.4. Road Accident Investigation Teams (RAIT), Finland ....................................14 3.4. Analysis technique and definitions .........................................................................15 3.4.1. Injury severity .................................................................................................15 3.4.2. Impact speed determination ............................................................................16 3.4.3. Head impact speed ..........................................................................................16 3.4.4. Head and body impact angle...........................................................................16 3.4.5. Collision types.................................................................................................17 3.4.6. Definition for mechanisms..............................................................................17 3.4.7. Replication process .........................................................................................18 3.5. Linkage of COST databank to national statistics....................................................18 3.6. Results of the analysis of the COST accident database ..........................................20 3.6.1. Effect of age ....................................................................................................20 3.6.2. Helmet mass distribution and loss ..................................................................21 3.6.3. Injury distribution............................................................................................22 3.6.4. Head injury severity and related factors..........................................................23 COST 327 3.6.5. Collision configuration ...................................................................................31 3.6.6. Neck injury...................................................................................................... 34 3.7. Head and neck injury mechanisms .........................................................................37 3.8. Effect of climatic conditions on accident risk.........................................................44 3.8.1. Introduction..................................................................................................... 44 3.8.2. Analysis........................................................................................................... 45 3.8.3. Comparison of climate conditions in the different countries.......................... 46 3.8.4. Climate conditions in accidents ...................................................................... 46 3.8.5. Visor condition and accident risk. .................................................................. 51 3.8.6. Analysis and results ........................................................................................ 52 3.9. Conclusions.............................................................................................................56 CHAPTER 4. HEADFORM ASSESSMENT ...................................................................59 4.1. Introduction.............................................................................................................59 4.2. Characteristics of existing headforms.....................................................................59 4.2.1. Wooden headform........................................................................................... 59 4.2.2. Aluminium headform...................................................................................... 59 4.2.3. Hybrid II dummy head.................................................................................... 60 4.2.4. Hybrid III dummy head .................................................................................. 60 4.2.5. Bimass head form ........................................................................................... 60 4.3. Impact response ......................................................................................................62 4.3.1. Introduction....................................................................................................
Load more

Recommended publications
  • Motorcycle Protective Clothing
    MOTORCYCLE PROTECTIVE CLOTHING: PROTECTION FROM INJURY OR JUST THE WEATHER? Liz de Rome (a), Rebecca Ivers(a), Michael Fitzharris (c), Wei Du (a), Narelle Haworth (d), Stephane Heritier (a), Drew Richardson (b). Author Affiliations: a. The George Institute for Global Health, The University of Sydney, Australia b. Medical School, Australian National University, Australia c. Accident Research Centre, Monash Injury Research Institute, Monash University, Australia d. CARRS-Q, Queensland University of Technology, Australia Corresponding author: Ms Liz de Rome, Injury Division, The George Institute for Global Health Postal address: PO Box M201, Missenden Road, Sydney NSW 2050 Australia Phone: +61 2 9657 0361 /Fax: +61 2 9657 0301 Email: [email protected] ABSTRACT Background: Apart from helmets, little is known about the effectiveness of motorcycle protective clothing in reducing injuries in crashes. The study aimed to quantify the association between usage of motorcycle clothing and injury in crashes. Methods: Cross-sectional analytic study. Crashed motorcyclists (n=212, 71% of identified eligible cases) were recruited through hospitals and motorcycle repair services. Data was obtained through structured face-to-face interviews. The main outcome was hospitalization and motorcycle crash-related injury. Poisson regression was used to estimate relative risk (RR) and 95% confidence intervals for injury adjusting for potential confounders. Results: Motorcyclists were significantly less likely to be admitted to hospital if they crashed wearing motorcycle jackets (RR=0.79, 95% CI: 0.69-0.91), pants (RR=0.49, 95% CI: 0.25-0.94), or gloves (RR=0.41, 95% CI: 0.26-0.66). When garments included fitted body armour there was a significantly reduced risk of injury to the upper body (RR=0.77, 95% CI: 0.66-0.89), hands and wrists (RR=0.55, 95% CI: 0.38-0.81), legs (RR = 0.60, 95% CI: 0.40-0.90), feet and ankles (RR=0.54, 95% CI: 0.35-0.83).
    [Show full text]
  • Motocross Isa Team Sport...Sure Most Consider Motorcycle Racing An
    Motocross IS a team sport ....Sure most consider motorcycle racing an Individual action. Yes, you can do It alone, but when we look at the big picture we clearly see there are so many elements that are Involved In the sport Many of us on the outside do not realize the behind scenes preparation The work that It takes ... From sign up to trophies .... An enormous amount of organization IS Involved April 17, 1978, a man by the name of Jerry Sharp opened a European style motocross track in Springfield, Missoun. The name of the track was Possum Hollow In dedication to their adventure In finding the ground At this time there were only three motocross tracks In the state of Mlssoun, Cycle World USA In SI. lOUIS, lake City In the Kansas City area, and Possum Hollow In Spnngfleld. For the next three years Jerry and wife, Ellie, promoted and organ- Ized motocross races at the Ozark Empire Fair Grounds and Possum Hollow It s said that Jerry was fifteen to twenty years ahead of his time In the arenacross style of racing. In 1981 Jerry started a senes that Included two tracks, Gene lewIs' lake City and his very own Possum Hollow. Tied to the GNC the events were qualifiers, at that time, for Ponca City and lake Whitney In Texas. As the years flew by Jerry continued his full time job With Gibson Greeting Cards travel- ing the states of Missoun and northern Arkansas puttmg In fifty to sixty hour weeks and still bUilding and promoting the senes.
    [Show full text]
  • Motorcycle and Moped Operator Manual Iii Escape Routes……………………………………
    Developed by The American Association of Motor Vehicle Administrators November 2012 This manual is a supplement to the state’s driver manual which covers rules of the road, signs, signals, roadway markings and safe driving practices. Graphics and pictures contained within this manual are provided courtesy of Motorcycle Safety Foundation and Highway Safety Services, LLC. eveloped by The American Association of Motor Vehicle Administrators November 2012 This manual is a supplement to the state’s driver manual which covers rules of the road, signs, signals, roadway markings and safe driving practices. Table of Contents SECTION 1 - Motorcycle Rider Licensing How to Obtain Your Motorcycle License/Permit… 1-2 Types of Motorcycle and Moped Licenses………. 1-3 Types of Motorcycles………………………........... 1-4 Mopeds ………………………….…..……………... 1-5 Required Motorcycle License Tests….………….. 1-8 Motorcycle Rider Training…………….…………… 1-9 Road Test Certificate……………...………………. 1-10 Street-Legal Motorcycle……………….………….. 1-10 Alcohol and the Law……………………………….. 1-11 Drugs and the Law………………..……………….. 1-12 South Carolina's Laws…………..…….................. 1-12 Specific Rules of the Road for Motorcycles……... 1-12 SECTION 2 - Being in Shape to Ride Alcohol, Other Drugs and Riding…………………. 2-1 Health………………………………..………………. 2-4 Emotions…………………………..………………… 2-4 SECTION 3 - Before You Ride Selecting and Wearing Protective Gear…………. 3 -1 Know Your Motorcycle…………………………….. 3-6 Motorcycle Controls………………………….......... 3-7 SECTION 4 - Vehicle Control Skills Getting Started……………………………………. 4-1 Riding in a Straight Line…………………….……. 4-2 Shifting Gears………………………………..……. 4-4 Stopping………………………………………..….. 4-5 Turning……………………………………….......... 4-6 SECTION 5 - Street Strategies Risk Awareness/Acceptance……………..……… 5-1 Risk Management………………………..……….. 5-3 Intersections…………………………………..…… 5-6 Space Management………………………………. 5-8 SC Motorcycle and Moped Operator Manual iii Escape Routes…………………………………….
    [Show full text]
  • Motorcyclists Hemets and Visors Test Methods and New Technologies
    This report has been produced by TRL Limited, under/as part of a Contract placed by the Department for Transport. Any views expressed are not necessarily those of the Department for Transport. TRL is committed to optimising energy efficiency, reducing waste and promoting recycling and re-use. In support of these environmental goals, this report has been printed on recycled paper, comprising 100% post- consumer waste, manufactured using a TCF (totally chlorine free) process. CONTENTS Abstract 1 Executive Summary 2 1 Introduction 5 2 Background 6 2.1 COST 327 6 2.2 Protective helmets: motorcycle, pedal cycle and human head tolerance (S100L/VF) 6 2.3 Project objectives 7 3 Strategic meetings, Inception Workshop and Conferences 8 3.1 Inception workshop 8 3.2 Break-point meeting 9 3.3 Meeting with Auto Cycle Union 9 3.4 ESV 2005 – Washington 6th to 9th June 2005 9 4 European collaboration through Framework Programme 6 11 5 Review of current test methods 12 5.1 COST 327 Proposals 12 5.2 Helmet retention 14 5.3 Method A and Method B alignment 28 5.4 Guided headform versus free-motion headform 44 5.5 Centre of gravity alignment for free-motion headforms 47 5.6 Extent of protection and points of impact 53 6 Bimass headform 62 6.1 General 62 6.2 Helmet optimisation 62 6.3 Results and conclusions 62 7 Helmet visors 64 7.1 General 64 7.2 Visor technology and draft performance requirements 64 7.3 Ambient light levels – verification of values from literature 65 8 Advanced helmets 66 9 Consumer Information Scheme (CIS) 67 9.1 Introduction 67 9.2 Accident Analysis 68 9.3 Test protocols 72 9.4 Assessment protocols 75 9.5 CIS pilot study 79 TRL Limited PPR 186 10 Discussion 84 10.1 Improved test methods 84 10.2 Mechanisms for delivering safer helmets 86 11 Conclusions 88 References 90 Appendix A.
    [Show full text]
  • Motorcycle & Moped Manual
    2020 - 2021 OREGON Motorcycle & Moped Manual Driver and Motor Vehicle Services Visit us at our web site www.OregonDMV.com Published by Oregon Department of Transportation Driver and Motor Vehicle Services 1905 Lana Avenue NE Salem, Oregon 97314 Graphics/Layout DMV Related Questions: (503) 945-5000 ODOT is an Equal Employment Opportunity and Afrmative Action Employer. ODOT does not discriminate on the basis of disability in admission or access to our programs, services, activities, hiring, and employment practices. To report any complaints or concerns related to discrimination, please call: 1-877-336-6368 (EEO-ODOT). Tis information can be made available in an alternative format by contacting a local DMV feld ofce. Te majority of the content of this manual is directly from the American Association of Motor Vehicle Administrator’s Motorcycle Operator Manual, with inserts from Motorcycle Safety Foundation, Team Oregon and particulars of Oregon law. Te purpose of the Oregon Motorcycle & Moped Manual is to help riders prepare for Oregon endorsement tests by providing a summary of the rules of the road and safe riding practices. Tis manual condenses and paraphrases selected language in the Oregon Revised Statutes. It also provides safety recommendations not included in law. Tis manual is not a source of law and should not be relied upon or cited as legal precedent in a court of law or other administrative or legal proceeding. Local governments may have additional ordinances not covered in this manual. Please check DMV’s website OregonDMV.com for updates, ofce locations and hours, fees and additional information. iv Contents Section One ................................................................................
    [Show full text]
  • Ktm Duke Range 2020 Range Duke Ktm En
    KTM DUKE RANGE 2020 EN KTM DUKE RANGE 2020 YOU DON‘T NEED A ROYAL BLOODLINE TO BE A COMPLETE BADASS. YOUR DUKEDOM STARTS HERE. 0.006 KTM 1290 SUPER DUKE R 0.038 KTM 390 DUKE 0.018 KTM 890 DUKE R 0.044 KTM 125 DUKE INDEX 0.028 KTM 790 DUKE 0.052 TECHNICAL DATA NO MORE EXCUSES. KTM 1290 SUPER DUKE R ALL NEW CHASSIS. 100 % DUKE SPIRIT. THE BEAST HAS EVOLVED. The KTM 1290 SUPER DUKE R is now leaner, meaner and more menacing than ever before. This is not a stripped-down sports bike. THE BEAST has been designed to be an extreme Naked bike from the ground up. Un-faired, unobstructed and unapologetically raw, proudly displaying its intentions in all 1301 cubic centimeters of its naked glory. 0.007 KTM 1290 SUPER DUKE R Raising a subliminal two-fingered salute to the opposition, the legendary V-twin engine powering THE BEAST has had a few tweaks. Additional top feeder injectors in the airbox have improved combustion throughout the entire rev range, while the larger diameter exhaust system ensures none of the signature brutality or V-twin roar has been lost. Cranking out a neck-snapping 180 hp and 140 Nm of torque, this powerhouse has been built to take on anything you’re brave enough to throw at it. THE SOUND OF SPEED 0.009 KTM 1290 SUPER DUKE R LAWSOF PHYSICS ARE MADE TO BE BROKEN At the core of the KTM 1290 SUPER DUKE R is a major chassis overhaul. It boasts three times the torsional rigidity of previous models thanks to an all-new frame and composite subframe.
    [Show full text]
  • Analysis Study of Current Transportation Status in Vietnam's
    sustainability Article Analysis Study of Current Transportation Status in Vietnam’s Urban Traffic and the Transition to Electric Two-Wheelers Mobility Duc Nguyen Huu * and Van Nguyen Ngoc Faculty of Energy Technology and Faculty of Electrical Engineering, Electric Power University, Hanoi 100000, Vietnam; [email protected] * Correspondence: [email protected]; Tel.: +84-90-1008-555 Abstract: In Vietnam’s major urban areas, private motorcycles are the main means of transportation that are suitable for socio-economic conditions, current transport infrastructure, and people’s habits. However, in recent years, the negative effects of a large number and high density of motorcycles in urban areas such as traffic congestion and noise and air pollution have resulted in a gradual change in the public’s opinion of private vehicle adoption, especially motorcycles. The public has also urged the authorities to issue policies of limiting or curving the growth in the number of private vehicles powered by fossil fuels in big cities. However, in order to achieve the goal, other alternative means of transport should be proposed to encourage people to move to a more sustainable and eco-friendly form of mobility. The alternatives also should be consistent with the average income level as well as social characteristics. In recent years, along with the development of a highly connected public transport network, efficient and less-polluting vehicles including electric two-wheelers have been emerging, thriving, and drawing more attraction from Vietnamese people and policy makers. The Citation: Huu, D.N.; Ngoc, V.N. spread in the number of electric two-wheelers in Vietnam’s major cities may be a sign of the transition Analysis Study of Current to a more sustainable and less-polluting means of transport as an alternative to gasoline-powered Transportation Status in Vietnam’s motorcycles.
    [Show full text]
  • 2021 AMA Amateur Competition Rulebook
    2021 RULEBOOK 2021 AMA Racing Rules Governing Pro/Am, Standard, ATV and Youth Competition An exclusive service to members of the American Motorcyclist Association The American Motorcyclist Association takes pride in its long record of achievement as the world’s largest sanctioning body for the sport of motorcycle competition. Since 1924 the objectives of the Association have been the same: to foster strong and fair competition, to provide reasonable guidelines for the various types of competition, and to provide an impartial competition program. The rules of competition are intended only as a guide for the conduct of the sport pursuant to uniform rules. Rules related to safety are made to make everyone concerned with safety. However, the AMA neither warrants safety if the rules are followed nor compliance with the enforcement of the rules. Moreover, each participant in competition has the responsibility to assess the safety aspects of facilities and conditions and must assume the risk of competition. Recognized and non-recognized districts, and organizations within a district, must submit any temporary or locally appropriate supplemental regulations for approval by the AMA Racing Department. Supplemental regulations may not be in conflict with national rules. In the event of a protest or appeal, the judgment will be based on information contained in the AMA national rules. Contact the AMA at (800) 262-5646 for the address of your district office. The American Motorcyclist Association (AMA) prohibits discrimination in all of its programs and activities (including all AMA-sanctioned events) on the basis of race, color, national origin, creed, religion, sex, age, disability, veteran status, marital status, familial status, parental status, sexual orientation, or any other category protected by applicable state or federal law.
    [Show full text]
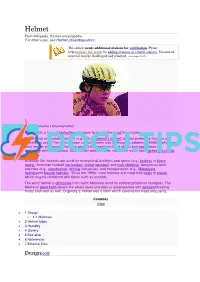
  • Helmet from Wikipedia, the Free Encyclopedia for Other Uses, See Helmet (Disambiguation)
    Helmet From Wikipedia, the free encyclopedia For other uses, see Helmet (disambiguation). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. (December 2012) A woman wearing a bicycling helmet A helmet is a form of protective gear worn to protect the head from injuries. Ceremonial or symbolic helmets (e.g., UK policeman's helmet) without protective function are sometimes used. The oldest known use of helmets was by Assyrian soldiers in 900BC, who wore thick leather or bronze helmets to protect the head from blunt object and swordblows and arrow strikes in combat. Soldiers still wear helmets, now often made from lightweight plastic materials. In civilian life, helmets are used for recreational activities and sports (e.g., jockeys in horse racing, American football, ice hockey, cricket,baseball, and rock climbing); dangerous work activities (e.g., construction, mining, riot police); and transportation (e.g., Motorcycle helmetsand bicycle helmets). Since the 1990s, most helmets are made from resin or plastic, which may be reinforced with fibers such as aramids. The word helmet is diminutive from helm, Medieval word for combat protective headgear. The Medieval great helm covers the whole head and often is accompanied with camail protecting throat and neck as well. Originally a helmet was a helm which covered the head only partly. Contents [hide] 1 Design o 1.1 Materials 2 Helmet types 3 Heraldry 4 Gallery 5 See also 6 References 7 External links Design[edit] A protective helmet worn during rock climbing All helmets attempt to protect the user's head by absorbing mechanical energy and protecting against penetration.
    [Show full text]
  • MTC Student Handbook V7
    California Motorcyclist Safety Program Motorcyclist Training Course Student Handbook Second Edition: February 2016 Copyright © 2016 Total Control Training, Inc. All rights reserved. No part of this publication may be reproduced or transmitted in any form by any means, electronic or mechanical, including photocopy, recording or any information and retrieval system, without permission from Total Control Training, Inc. Under no circumstances may the material be reproduced for resale. Please send requests in writing to: Total Control Training, Inc., 15329 Bonanza Road, Suite B, Victorville, CA 92392. Visit the CMSP website for more information on courses and course locations: www.californiamotorcyclist.com Motorcyclist Training Course Produced by Total Control Training, Inc. (www.totalcontroltraining.net) for the California Motorcyclist Safety Program Second Edition: February 2016 Foreword It’s about the journey, not the destination. The Motorcyclist Training Course offered by the California Motorcyclist Safety Program is designed to address the needs and interests of beginning riders. Our goal is to help you build a strong foundation of awareness and safety in what may develop into a lifelong activity. Because motorcycling requires mental and physical skills, we will focus on both throughout the course. You will learn techniques to help sharpen your judgment and perception as well as the physical skills required for riding. Learning is an ongoing process and doesn’t end when you finish a course. This beginner course is intended as a starting point from which to build lifelong skills. Becoming an experienced, skillful rider takes time and practice. That, of course, means riding and practicing the techniques presented in this course.
    [Show full text]
  • Trail of Cthulhu.Pdf
    TRAIL OF CTHULHU Credits Publisher: Simon Rogers Written by: Kenneth Hite GUMSHOE System: Robin D Laws Layout: Jérôme Huguenin Art: Jérôme Huguenin GUMSHOE Guru: Robin D Laws Editing and Additional Material: Simon Rogers Based on: Call of Cthulhu by Sandy Petersen and Lynn Willis Special thanks : Effie and Julia Huguenin, Léo and Pascal Quidault Playtesting: Adrian Price, Steve Dempsey, Wai Kien, Adrian Smith, Graham Walmsley, Alex Fradera, Dave, Polymancer Studios, Simon Rogers, Daniel Bayn, Danni Bayn, Chris Malone, Mark DiPasquale, Matthew Pook, Tim Barker, Louise Hayes, David Lai, Mike Shepard, Carla Jane Miller, Elizabeth Rees, Robert Mills, Donald F. Taylor III, Richard Hardy, Lynne Hardy, Frederic Moll, Fredrik Hansson, Jeff Campbel Jamie Michael, Joshua Ford, Marcus Ogawa, Lisa Marie Ogawa, Gil Trevizo, Henry de Veuve, Ronald Abitz, Steve Bartalamay, Alan Fountain, Peter Kessler, Wojciech “Alter” Kobza, Laurent Mollicone, Olivier Noël, Wayne O’Connor, Ghislain Morel, James Semple, Gabriella Semple, Dan Pusceddu, Olive Pusceddu, Axel Eble, Stefan Ohrmann, Martin Schrammm, Onno Tasler, Ralf Achenbach, William C Bargo Jr, Jacques Maurice Mallah, Donald F. Taylor III, Keith A Callison, Doug © 2007 Pelgrane Press Ltd. All Rights Reserved. Published by arrangement with Chaosium, Inc. Trail of Cthulhu is a trademark of Pelgrane Press Ltd. 3 TRAIL OF CTHULHU Contents CREDITS ...........................................................3 Cop Talk (Interpersonal) ...................32 Piggybacking ...........................................
    [Show full text]
  • Technical Rules Motocross Règlements Techniques
    TECHNICAL RULES MOTOCROSS (INCLUDING RULES FOR QUADS, SUPERMOTO & SNOWCROSS) 2021 RÈGLEMENTS TECHNIQUES MOTOCROSS (RÈGLEMENTS POUR QUADS, SUPERMOTO & MOTONEIGE INCLUS) Technical Rules Motocross (Including Rules for Supermoto, Sidecars, Quads and Snowcross) 2021 Règlements Techniques Motocross (Règlements pour Supermoto, Sidecars, Quads et Motoneige inclus) Version 0 Applicable as from 23.02.2021 1 YEAR 2021 Version Applicable as from Modified paragraphs 0 23.01.2021 01.07, 25.01, 01.28, 31.05, 37.03, 43.07, 01.70, 01.51 2 Table of contents 01.01 INTRODUCTION ....................................................................................... 4 01.03 FREEDOM OF CONSTRUCTION ............................................................ 4 01.05 CATEGORIES AND GROUPS OF MOTORCYCLES ............................... 4 01.07 CLASSES.................................................................................................. 5 01.11 MEASUREMENT OF CAPACITY ............................................................. 6 01.17 SUPERCHARGING .................................................................................. 7 01.18 TELEMETRY ............................................................................................. 8 01.19 MOTORCYCLE WEIGHTS ....................................................................... 8 01.21 DESIGNATION OF MAKE ........................................................................ 9 01.23 DEFINITION OF A PROTOTYPE ............................................................. 9 01.25 GENERAL
    [Show full text]