Integration of Myofibrils in the Developing Heart and Challenges on the Intercalated Disc Stability
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Purification and Partial Characterization of a Coagulant Tle
Received: September 4, 2008 J Venom Anim Toxins incl Trop Dis. Accepted: February 13, 2009 V.15, n.3, p.411-423, 2009. Abstract published online: March 5, 2009 Original paper. Full paper published online: August 31, 2009 ISSN 1678-9199. PURIFICATION AND PARTIAL CHARACTERIZATION OF A COAGULANT SERINE PROTEASE FROM THE VENOM OF THE IRANIAN SNAKE Agkistrodon halys Ghorbanpur M (1), Zare Mirakabadi A (2), Zokaee F (1), Zolfagarrian H (2), Rabiei H (2) (1) Chemical Engineering Department, Amirkabir University, Tehran, Iran; (2) Department of Venomous Animals and Antivenom Production, Razi Vaccine and Serum Research Institute, Karaj, Iran. ABSTRACT: Agkistrodon halys is one of several dangerous snake species in Iran. Among the most important signs and symptoms in patients envenomated by this snake is disseminated intravascular coagulation. A thrombin-like enzyme, called AH143, was isolated from Agkistrodon halys venom by gel filtration on a Sephadex G-50 column, ion-exchange chromatography on a DEAE-Sepharose and high performance liquid chromatography (HPLC) on a C18 column. In the final stage of purification, 0.82 mg of purified enzyme was obtained from 182.5 mg of venom. The purified enzyme showed a single protein band by sodium dodecyl sulfate polyacrylamide gel electrophoresis (SDS-PAGE), under reducing conditions, and its molecular mass was found to be about 30 kDa. AH143 revealed clotting activity in human plasma, which was not inhibited by EDTA or heparin. This enzyme still demonstrated coagulation activity when exposed to variations in temperature and pH ranging, respectively, from 30 to 40°C and from 7.0 to 8.0. -

9Th & 10Th Grade
1/27/2019 SpeechWire Tournament Services Ridge Invitational Declamation (9th & 10th Grade) Elimination round results Final round All Judges Code Name Team LK1 WK1 AA1 All ranks Place recips pref. AH101 Niamh Campbell Phoenix Country Day School 1 1 6 14 6.67 1 LP103 Matthew Floyd Catholic Memorial 2 2 1 15 5.25 2 BD109 Ashin Varghese Randolph High School 3 3 2 16 5.42 3 AO121 Juliette Gringeri Summit High School 5 4 4 23 3.95 4 UT102 Farrah Culmer Democracy Prep Harlem Prep 7 6 3 24 4.48 5 AH108 Enzo Acharya Phoenix Country Day School 6 5 7 26 4.01 6 AG101 Brynn Nelson Fontbonne Hall Academy 4 7 5 26 3.84 7 Semifinal round All Judges Code Name Team AP2 BD1 All ranks Place recips pref. AH101 Niamh Campbell Phoenix Country Day School 1 1 6 4.50 1 BD109 Ashin Varghese Randolph High School 8 4.25 2 UT102 Farrah Culmer Democracy Prep Harlem Prep 8 3.83 3 AH108 Enzo Acharya Phoenix Country Day School 8 3.50 4 AG101 Brynn Nelson Fontbonne Hall Academy 10 3.25 5 AO121 Juliette Gringeri Summit High School 10 3.25 5 LP103 Matthew Floyd Catholic Memorial 2 2 10 3.25 5 AG102 Juliann Bianco Fontbonne Hall Academy 11 3.53 8 AL101 Adrian Tejada Democracy Prep Endurance High 11 3.00 9 AH112 Milan Sewell Phoenix Country Day School 12 2.58 10 BC115 Maria Chabanov Xaverian HS 13 2.08 11 AH109 Devan Amin Phoenix Country Day School 14 2.37 12 GG105 Uswad Qureshi Phillipsburg HS 14 2.33 13 AC107 Nina Li Strath Haven High School 3 4 14 1.92 14 BC116 Amy Gruber Xaverian HS 15 2.70 15 AH133 Ella Brenes Phoenix Country Day School 4 5 15 2.28 16 AM101 Jaina Jallow Livingston High School 5 3 15 1.87 17 AK108 Fatimata Ly Achievement First 17 2.60 18 CZ112 Rajit Sharma Union Catholic 17 2.03 19 Semifinal round All Judges Code Name Team AA5 RY3 All ranks Place recips pref. -
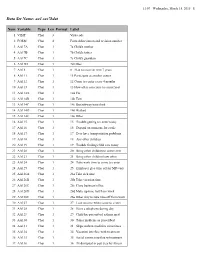
Childhood Asthma Management Program Data Dictionary
11:07 Wednesday, March 18, 2015 1 Data Set Name: aa1.sas7bdat Num Variable Type Len Format Label 1 VISIT Char 3 Visit code 2 FORM Char 4 Form abbreviation and revision number 3 AA17A Char 1 7a Child's mother 4 AA17B Char 1 7b Child's father 5 AA17C Char 1 7c Child's guardian 6 AA17D Char 1 7d Other 7 AA18 Char 1 8 Plan to move in next 7 years 8 AA111 Char 1 11 Participate at another center 9 AA112 Char 1 12 Come to center every 4 months 10 AA113 Char 1 13 How often can come to center/year 11 AA114A Char 1 14a Car 12 AA114B Char 1 14b Taxi 13 AA114C Char 1 14c Bus/subway/metrolink 14 AA114D Char 1 14d Walked 15 AA114E Char 1 14e Other 16 AA115 Char 1 15 Trouble getting to center today 17 AA116 Char 1 16 Depend on someone for a ride 18 AA117 Char 1 17 Ever have transportation problems 19 AA118 Char 1 18 Any other children 20 AA119 Char 1 19 Trouble finding child care today 21 AA120 Char 1 20 Bring other children to center ever 22 AA121 Char 1 21 Bring other children how often 23 AA124 Char 1 24 Take work time to come to center 24 AA125 Char 1 25 Employer give time off for MD visit 25 AA126A Char 1 26a Take sick time 26 AA126B Char 1 26b Take vacation time 27 AA126C Char 1 26c Close business/office 28 AA126D Char 1 26d Make up time lost from work 29 AA126E Char 1 26e Other way to take time off from work 30 AA127 Char 1 27 Lose income when come to center 31 AA128 Char 1 28 Have a telephone during day 32 AA129 Char 1 29 Child has prescribed asthma med 33 AA130 Char 1 30 Takes medicine as prescribed 34 AA131 Char 1 31 Skips asthma medicine -

Before the Public Service Commission of the State of Missouri
BEFORE THE PUBLIC SERVICE COMMISSION OF THE STATE OF MISSOURI In the Matter of Kansas City Power & Light ) Company’s Notice of Intent to File an ) Application for Authority to Establish a Demand- ) File No. EO-2015-0240 Side Programs Investment Mechanism ) In the Matter of KCP&L Greater Missouri Operations ) Company’s Notice of Intent to File an ) Application for Authority to Establish a Demand- ) File No. EO-2015-0241 Side Programs Investment Mechanism ) RESPONSE TO ORDER APPROVING APPLICATION TO MODIFY TECHNICAL RESOURCE MANUAL AND PROGRAM DESIGN INCENTIVE RANGES COMES NOW Kansas City Power & Light Company and KCP&L Greater Missouri Operations Company (the “Company”) and, in response Ordered Paragraph 2 of the Missouri Public Service Commission’s (“Commission”) March 21, 2018 Order Approving Application to Modify Technical Resource Manual and Program Design Incentive Ranges (“Order”), files the attached amended Appendix 1 and Appendix 2 (collectively referred to as “Amended Appendices”) to the Non-Unanimous Stipulation and Agreement (originally approved by the Commission on April 6, 2016). The Amended Appendices incorporate all modifications approved by the Commission in its Order. WHEREFORE, the Company respectfully requests the Commission consider this response to the Commission’s Order. Respectfully submitted, /s/ Roger W. Steiner Robert J. Hack MBN 36496 Roger W. Steiner MBN 39586 Kansas City Power & Light Company 1200 Main Street, 16th Floor Kansas City, MO 64105 (816) 556-2785 (Phone) (816) 556-2787 (Fax) [email protected] [email protected] James M. Fischer MBN 27543 Fischer & Dority, P.C. 101 Madison Street, Suite 400 Jefferson City, MO 65101 (573) 636-6758 (Phone) (573) 636-0383 (Fax) [email protected] Attorneys for Kansas City Power & Light Company and KCP&L Greater Missouri Operations Company CERTIFICATE OF SERVICE I do hereby certify that a true and correct copy of the foregoing document has been hand delivered, emailed or mailed, postage prepaid, this 26th day of March, 2018, to all counsel of record. -

Technical Assistance Layout with Instructions
Resettlement Plan August 2017 INO: Flood Management in Selected River Basins Sector Project Prepared by the Ministry of Public Works and Housing through the Directorate General of Water Resources for the Asian Development Bank. This is an updated and revised version of the draft originally posted in May 2015 available on http://www.adb.org/projects/35182-043/main#project- documents. CURRENCY EQUIVALENTS (as of 11 August 2016) Rp1.00 = $0.000076 $1.00 = Rp13,129 ABBREVIATIONS ADB – Asian Development Bank AH – affected household AP – affected person BAPPEDA – Badan Perencanaan Pembangunan Daerah (Provincial/District Development Planning Agency) BPN – Badan Pertanahan Nasional (National Land Agency) BWS – Balai Wilayah Sungai (Center for River Basin) CBFRM – community-based flood risk management COI – corridor of impact CWZ – construction works zone DED – detailed engineering design DGWR – Directorate General of Water Resources DMS – detailed measurement survey EA – executing agency EIA – environmental impact assessment EMA – External Monitoring Agency FMSRBSP – Flood Management in Selected River Basins Sector Project GOI – Government of Indonesia HH – household IA – Implementing agency IOL – inventory of losses IR – involuntary resettlement Km – kilometer LA – Land acquisition LAIT – land acquisition implementation team LRP – livelihood restoration program MAPPI – Masyarakat Profesi Penilai Indonesia (Indonesian Professional Appraiser Association) MOHA – Ministry of Home Affairs NJOP – Nilai Jual Object Pajal (tax object selling price) PIB -

Affordable Housing Supplementary Planning Document (2006)
London Borough of Hillingdon LOCAL DEVELOPMENT FRAMEWORK AFFORDABLE HOUSING SUPPLEMENTARY PLANNING DOCUMENT (2006) STATEMENTS OF CONSULTATION AND SUSTAINABILITY APPRAISAL Policy and Environmental Planning Team Planning and Transportation Group London Borough of Hillingdon MAY 2006 0 Statements of Consultation and Sustainability Appraisal CONTENTS 1.0 INTRODUCTION 2.0 CONSULTATION STATEMENT 2.1 Consultation arrangements 2.2 Comments received 3.0 SUSTAINABILITY APPRAISAL (SA) 3.1 Purpose of this statement and the questions it responds to 3.2 Integration of environmental considerations 3.3 Consultation 3.4 Reasons for choosing the adopted SPD 3.5 Monitoring 4.0 OUTCOME APPENDICES APPENDIX 1 – List of SPD and Sustainability Appraisal consultees APPENDIX 2 – Summary of representations and the council’s response Affordable Housing SPD London Borough of Hillingdon 1 Statements of Consultation and Sustainability Appraisal 1.0 INTRODUCTION 1.1 This document accompanies the adopted Hillingdon Affordable Housing SPD and it brings together the requirements under the Strategic Environmental Assessment (SEA) Directive (2001) and the Town and Country Planning Act 2004 for the preparation of both a Sustainability Appraisal Statement and a Consultation Statement at the adoption stage of any Supplementary Planning Document. 1.2 The Consultation Statement (Section 2 of this document) sets out the public participation and consultation process undertaken for the Affordable Housing SPD in accordance with regulation 18 (4) (b) of the Town and Country Planning (local Development) (England) Regulations 2004. 1.3 The preparation of the Sustainability Appraisal Statement (section 3 of this document) responds to the requirements of Article 9 of European Directive 2001/42/EC (Strategic Environmental Assessment (SEA) Directive), the Office of the Deputy Prime Minister’s ‘Sustainability Appraisal for Regional Spatial Strategies and Local Development Documents’ (2005) and ‘Environmental Assessment of Plans and Regulations’, (2004). -

Report Prepared for the WPCS- 2015 a Preliminary Examination of the Genetic Variation Within and Between the Improvement Society Herds of Welsh Mountain Ponies
Aberystwyth University A preliminary examination of the genetic variation within and between the Improvement Society herds of Welsh Mountain ponies McMahon, Robert; Debbonaire, Aliyah; McEwan, Neil; Nash, Deborah; Davies-Morel, Mina; Winton, Clare Louise; Blackmore, Tina; Hegarty, Matthew Publication date: 2015 Citation for published version (APA): McMahon, R., Debbonaire, A., McEwan, N., Nash, D., Davies-Morel, M., Winton, C. L., Blackmore, T., & Hegarty, M. (2015). A preliminary examination of the genetic variation within and between the Improvement Society herds of Welsh Mountain ponies. Document License CC BY General rights Copyright and moral rights for the publications made accessible in the Aberystwyth Research Portal (the Institutional Repository) are retained by the authors and/or other copyright owners and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights. • Users may download and print one copy of any publication from the Aberystwyth Research Portal for the purpose of private study or research. • You may not further distribute the material or use it for any profit-making activity or commercial gain • You may freely distribute the URL identifying the publication in the Aberystwyth Research Portal Take down policy If you believe that this document breaches copyright please contact us providing details, and we will remove access to the work immediately and investigate your claim. tel: +44 1970 62 2400 email: [email protected] Download date: 29. Sep. 2021 Report prepared for the WPCS- 2015 A preliminary examination of the genetic variation within and between the Improvement Society herds of Welsh Mountain ponies Rob McMahon, Aliyah Debbonaire, Neil McEwan, Debbie Nash, Mina Davies-Morel, Clare Winton, Tina Blackmore and Matthew Hegarty Nov. -

HQ Ful-Grip Sheaves-Single Groove for Both Belt Sections "A" (4L) and "O" (3L) D.D
HQ Ful-Grip Sheaves-Single Groove For Both Belt Sections "A" (4L) and "O" (3L) D.D. D.D. Original Dimensions - Inches O.D. A Belts O Belts Part Maurey Style Weight Inches Inches Inches Number Number (Lbs) F L P C X G 3.05 2.8 2.5 AK30H --- 1 1.1 3/4 1 1/4 7/8 --- 1-3/16 7/16 3.25 3.0 2.7 AK32H --- 1 1.2 3/4 1 1/4 7/8 --- 1-3/16 7/16 3.45 3.2 2.9 AK34H --- 2 1.0 3/4 1 1/4 9/16 --- 7/8 7/16 3.75 3.5 3.2 AK39H --- 2 1.4 3/4 1 1/4 9/16 --- 7/8 7/16 3.95 3.7 3.4 AK41H AH40 2 1.6 3/4 1 1/4 9/16 --- 7/8 7/16 4.25 4.0 3.7 AK44H AH43 2 1.9 3/4 1 1/4 9/16 --- 7/8 7/16 4.45 4.2 3.9 AK46H AH45 2 1.9 3/4 1 1/4 9/16 --- 7/8 7/16 4.75 4.5 4.2 AK49H AH48 2 2.1 3/4 1 1/4 9/16 --- 7/8 7/16 4.95 4.7 4.4 AK51H AH50 2 2.3 3/4 1 1/4 9/16 --- 7/8 7/16 5.25 5.0 4.7 AK54H AH53 2 2.0 3/4 1 1/4 9/16 --- 7/8 7/16 5.45 5.2 4.9 AK56H AH55 2 2.3 3/4 1 1/4 9/16 --- 7/8 7/16 5.75 5.5 5.2 AK59H --- 2 2.4 3/4 1 1/4 9/16 --- 7/8 7/16 5.95 5.7 5.4 AK61H AH60 4 2.5 3/4 1 1/4 9/16 0 7/8 7/16 6.25 6.0 5.7 AK64H AH63 4 2.7 3/4 1 1/4 9/16 0 7/8 7/16 6.45 6.2 5.9 AK66H AH65 4 2.8 3/4 1 1/4 9/16 0 7/8 7/16 6.75 6.5 6.2 AK69H AH68 4 2.9 3/4 1 1/4 9/16 0 7/8 7/16 6.95 6.7 6.6 AK71H AH70 4 3.1 3/4 1 1/4 9/16 0 7/8 7/16 7.25 7.0 6.7 AK74H AH73 4 3.3 3/4 1 1/4 9/16 0 7/8 7/16 7.75 7.5 7.2 AK79H AH78 4 3.5 3/4 1 1/4 9/16 0 7/8 7/16 7.95 7.7 7.4 AH80 --- 4 2.9 3/4 1 1/4 9/16 0 7/8 7/16 8.25 8.0 7.7 AK84H AH83 4 3.6 3/4 1 1/4 9/16 0 7/8 7/16 8.75 8.5 8.2 AK89H AH88 4 4.0 3/4 1 1/4 9/16 0 7/8 7/16 8.95 8.7 8.4 AH90 --- 4 2.8 3/4 1 1/4 9/16 0 7/8 7/16 9.25 9.0 8.7 AK94H AH93 4 4.4 3/4 1 -

The Maximum Diversity Assortment Selection Problem
Takustr. 7 Zuse Institute Berlin 14195 Berlin Germany FELIX PRAUSE1,KAI HOPPMANN-BAUM2,BORIS DEFOURNY3,THORSTEN KOCH4 The Maximum Diversity Assortment Selection Problem 1 0000-0001-9401-3707 2 0000-0001-9184-8215 3 0000-0003-0405-5538 4 0000-0002-1967-0077 ZIB Report 20-34 (Dezember 2020) Zuse Institute Berlin Takustr. 7 14195 Berlin Germany Telephone: +49 30-84185-0 Telefax: +49 30-84185-125 E-mail: [email protected] URL: http://www.zib.de ZIB-Report (Print) ISSN 1438-0064 ZIB-Report (Internet) ISSN 2192-7782 The Maximum Diversity Assortment Selection Problem Felix Prause1[0000−0001−9401−3707], Kai Hoppmann-Baum1;2[0000−0001−9184−8215], Boris Defourny3[0000−0003−0405−5538], and Thorsten Koch1;2[0000−0002−1967−0077] 1 Zuse Institute Berlin, Takustr. 7, 14195 Berlin, Germany {prause,hoppmann-baum,koch}@zib.de 2 TU Berlin, Chair of Software and Algorithms for Discrete Optimization, Str. des 17. Juni 135, 10623 Berlin, Germany 3 Lehigh University, Department of Industrial and Systems Engineering, 200 W Packer Ave, Bethlehem, PA, 18015, USA [email protected] Abstract. In this paper, we introduce the Maximum Diversity Assort- ment Selection Problem (MADASS), which is a generalization of the 2-dimensional Cutting Stock Problem (2CSP). Given a set of rectan- gles and a rectangular container, the goal of 2CSP is to determine a subset of rectangles that can be placed in the container without overlap- ping, i.e., a feasible assortment, such that a maximum area is covered. In MADASS, we need to determine a set of feasible assortments, each of them covering a certain minimum threshold of the container, such that the diversity among them is maximized. -

CHIS 2020 Adult CATI Questionnaire (Interviewer- Administered) Version 1.16 April 19, 2021 Adult Respondents Age 18 and Older
CHIS 2020 Adult CATI Questionnaire (Interviewer- administered) Version 1.16 April 19, 2021 Adult Respondents Age 18 and Older Collaborating Agencies: • UCLA Center for Health Policy Research • California Department of Health Care Services • California Department of Public Health Contact: California Health Interview Survey UCLA Center for Health Policy Research 10960 Wilshire Blvd, Suite 1550 Los Angeles, CA 90024 Telephone: (866) 275-2447 Fax: (310) 794-2686 Web: www.chis.ucla.edu Copyright © 2020 by the Regents of the University of California CHIS 2020 Adult Questionnaire Version 1.16 April 19, 2021 Table of Contents Section A: Demographic Information, Part I ......................................................................................... 6 Age ......................................................................................................................................................... 6 Gender Identity ...................................................................................................................................... 8 Ethnicity ................................................................................................................................................. 9 Race ..................................................................................................................................................... 10 Language Spoken at Home ................................................................................................................. 15 Additional Language Use .................................................................................................................... -

CHIS 2021 Adult CAWI Questionnaire (Self- Administered) Version 1.28 May 17, 2021 Adult Respondents Age 18 and Older
CHIS 2021 Adult CAWI Questionnaire (Self- administered) Version 1.28 May 17, 2021 Adult Respondents Age 18 and Older Collaborating Agencies: • UCLA Center for Health Policy Research • California Department of Health Care Services • California Department of Public Health Contact: California Health Interview Survey UCLA Center for Health Policy Research 10960 Wilshire Blvd, Suite 1550 Los Angeles, CA 90024 Telephone: (866) 275-2447 Fax: (310) 794-2686 Web: www.chis.ucla.edu Copyright © 2021 by the Regents of the University of California CHIS 2021 Adult Questionnaire Version 1.28 May 17, 2021 Table of Contents Section A: Demographic Information, Part I ......................................................................................... 7 Age ......................................................................................................................................................... 7 Gender Identity ...................................................................................................................................... 8 Ethnicity ................................................................................................................................................. 9 Race ..................................................................................................................................................... 10 Language Spoken at Home ................................................................................................................. 15 Additional Language Use ....................................................................................................................