Axial Variation of Xylem Conduits in the Earth's Tallest Trees
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

A Comparative Study of the Primary Vascular System Of
ArneI'. J. Bot. 5.5(4): 447-457. 1968. A COMPARATIVE STUDY OF THE PRIMARY VASCULAR SYSTElVI OF CONIFERS. 1. GENERA WITH HELICAL PHYLLOTAXISl KADAMBARI K. N AMBOODIRI2 AND CHARLES B. BECK Department of Botany, University of Michigan, Ann Arbor ABSTRACT The primary vascular system of 23 species belonging to 18 genera of conifers with helical phyllotaxis has been investigated with the intent of determining the architecture .f the system. Special attention has been given to nodal and subnodal relations of the vascular bundles. The vascular system seems to be composed solely of relatively discrete sympodia, that is, axial vascu lar bundles from which leaf traces branch unilaterally. Although the discreteness of the syrn podia is not immediately apparent because of their undulation and lateral contacts with neigh boring ones, close examination, including a statistical analysis of the tangential contacts, seems to reveal that each sympodium maintains its identity throughout. Although two traces may be apparent at nodal levels, the trace supply to a leaf originates, in all species, as a single bundle. An analysis is made of the relationship between the vasculature and the phyllotaxis. It is ob served that the direction of trace divergence can be accurately predicted when the direction of the ontogenetic spiral, the angle of divergence of leaf traces, and the number of syrnpodia are known. THE ORIGIN and evolution of gymnosperms that of the ferns by reduction (Jeffrey, 1902, are significant problems that deserve increased 1917). Consequently, he considered the leaf gap attention. There have been few modern compara of seed plants to be homologous with that of tive studies of extant gymnosperms, and most the ferns. -

Principal Types of Vegetative Shoot Apex Organization in Vascular Plants1
PRINCIPAL TYPES OF VEGETATIVE SHOOT APEX ORGANIZATION IN VASCULAR PLANTS1 RICHARD A. POPHAM Department of Botany and Plant Pathology, The Ohio State University, Columbus 10 Before progress can be made in research, a problem must be recognized. Once the problem has been perceived, a research program may be directed toward a solution. The problem of how and where a shoot grows and the organization of the shoot apex was apparently first conceived by Kaspar Friedrich Wolff (1759). Although his observations on the structure, formation, and growth of cells were fantastically inaccurate, he made a great contribution to our knowledge of the growing plant by setting forth a new and important problem. In a very real sense, Wolff is the father of developmental plant anatomy. Disagreement is the life blood of many research problems. Strenuous opposition is often engendered by a dogmatic statement or a theory which is proposed as a universal truth. Opposition to Wolff's (1759) original proposition regarding the organization and growth of shoot apices prompted plant anatomists, some 85 years later, to investigate the truth of the statement. The factual solution of the problem of shoot apex organization had its beginnings in the work of Nageli (1845). Following this work on many lower cryptogams, Nageli concluded that the cells of all tissues of the shoot of cryptogams and higher plants have their genesis in a single apical cell. The new-born apical cell theory supported by Hofmeister (1851) and others provided the impetus for a renewed, vigorous attack on the problem of shoot apex organization. A little later a new proposal, Hanstein's (1868) histogen theory was born of more careful observations and in a mind unfettered by the prevailing fanaticism of the apical cell theorists. -

2021 Plant List
2021 Plant List New items are listed with an asterisk (*) Conifers Pinus thungerbii Abies koreana 'Horstmann's Silberlocke' Pinus x 'Jane Kluis' * Chamaecyparis nootkatensis 'Pendula' Sciadopitys vert. 'Joe Dozey' Chamaecyparis noot. 'Glauca Pendula' Sciadopitys vert. 'Wintergreen' Chamaecyparis obtusa 'Chirimen' * Taxodium distichum 'Pendula' Chamaecyparis obtusa 'Gracilis' -Select Taxodium distichum 'Peve Mineret' Chamaecyparis obtusa 'Kosteri' Taxus cuspidaata 'Nana Aurescens' Chamaecyparis obtusa 'Nana' Tsuga con. 'Jervis' Chamaecyparis obtusa 'Nana Gracilis' Chamaecyparis obtusa 'Spiralis' Ferns Chamaecyparis obtusa 'Thoweil' Adiantum pedatum ….Maiden Hair Chamaecyparis obtusa 'Verdoni' Athyrum filix-femina 'Minutissima' Juniperus procumbens 'Nana' Athyrium 'Ghost' Larix decidua 'Pendula' Athyrum niponicum 'Godzilla' Larix decidua 'Pendula' -Prostrate Form Athyrum niponicum 'Pictum' Picea abies 'Hasin' * Athyrum niponicum pic. 'Pearly White' Picea abies 'Pusch' * Dennstaedtia punctilobula Picea omorika 'Nana' Dryopteris ery. 'Brilliance' Picea omorika 'Pendula' Dryopteris marginalis Picea orientalis 'Nana' Matteucciastruthiopteris var. pensylvanica Picea orientalis 'Shadow's Broom' * Osmunda cinnamomea Picea pungens 'Glauca Globosa' Polystichum acrostichoides Pinus mugo 'Mughus' - Rock Garden Strain Polystichum polyblepharum Pinus mugo 'Slowmound' Pinus nigra 'Hornibrookiana' Grasses Pinus parviflora 'Aoi' These are but a fraction of the grasses we'll be Pinus parviflora 'Glauca Nana' offering this year. Many more to come. They'll -

Gymnosperms on the EDGE Félix Forest1, Justin Moat 1,2, Elisabeth Baloch1, Neil A
www.nature.com/scientificreports OPEN Gymnosperms on the EDGE Félix Forest1, Justin Moat 1,2, Elisabeth Baloch1, Neil A. Brummitt3, Steve P. Bachman 1,2, Stef Ickert-Bond 4, Peter M. Hollingsworth5, Aaron Liston6, Damon P. Little7, Sarah Mathews8,9, Hardeep Rai10, Catarina Rydin11, Dennis W. Stevenson7, Philip Thomas5 & Sven Buerki3,12 Driven by limited resources and a sense of urgency, the prioritization of species for conservation has Received: 12 May 2017 been a persistent concern in conservation science. Gymnosperms (comprising ginkgo, conifers, cycads, and gnetophytes) are one of the most threatened groups of living organisms, with 40% of the species Accepted: 28 March 2018 at high risk of extinction, about twice as many as the most recent estimates for all plants (i.e. 21.4%). Published: xx xx xxxx This high proportion of species facing extinction highlights the urgent action required to secure their future through an objective prioritization approach. The Evolutionary Distinct and Globally Endangered (EDGE) method rapidly ranks species based on their evolutionary distinctiveness and the extinction risks they face. EDGE is applied to gymnosperms using a phylogenetic tree comprising DNA sequence data for 85% of gymnosperm species (923 out of 1090 species), to which the 167 missing species were added, and IUCN Red List assessments available for 92% of species. The efect of diferent extinction probability transformations and the handling of IUCN data defcient species on the resulting rankings is investigated. Although top entries in our ranking comprise species that were expected to score well (e.g. Wollemia nobilis, Ginkgo biloba), many were unexpected (e.g. -

Common Name Scientific Name Type Plant Family Native
Common name Scientific name Type Plant family Native region Location: Africa Rainforest Dragon Root Smilacina racemosa Herbaceous Liliaceae Oregon Native Fairy Wings Epimedium sp. Herbaceous Berberidaceae Garden Origin Golden Hakone Grass Hakonechloa macra 'Aureola' Herbaceous Poaceae Japan Heartleaf Bergenia Bergenia cordifolia Herbaceous Saxifragaceae N. Central Asia Inside Out Flower Vancouveria hexandra Herbaceous Berberidaceae Oregon Native Japanese Butterbur Petasites japonicus Herbaceous Asteraceae Japan Japanese Pachysandra Pachysandra terminalis Herbaceous Buxaceae Japan Lenten Rose Helleborus orientalis Herbaceous Ranunculaceae Greece, Asia Minor Sweet Woodruff Galium odoratum Herbaceous Rubiaceae Europe, N. Africa, W. Asia Sword Fern Polystichum munitum Herbaceous Dryopteridaceae Oregon Native David's Viburnum Viburnum davidii Shrub Caprifoliaceae Western China Evergreen Huckleberry Vaccinium ovatum Shrub Ericaceae Oregon Native Fragrant Honeysuckle Lonicera fragrantissima Shrub Caprifoliaceae Eastern China Glossy Abelia Abelia x grandiflora Shrub Caprifoliaceae Garden Origin Heavenly Bamboo Nandina domestica Shrub Berberidaceae Eastern Asia Himalayan Honeysuckle Leycesteria formosa Shrub Caprifoliaceae Himalaya, S.W. China Japanese Aralia Fatsia japonica Shrub Araliaceae Japan, Taiwan Japanese Aucuba Aucuba japonica Shrub Cornaceae Japan Kiwi Vine Actinidia chinensis Shrub Actinidiaceae China Laurustinus Viburnum tinus Shrub Caprifoliaceae Mediterranean Mexican Orange Choisya ternata Shrub Rutaceae Mexico Palmate Bamboo Sasa -

Occurrence of Sciadopitys-Like Fossil Wood (Coniferales) in the Jurassic of Western Liaoning and Its Evolutionary Implications
Letter Geology February 2012 Vol.57 No.6: 569572 doi: 10.1007/s11434-011-4850-z SPECIAL TOPICS: Occurrence of Sciadopitys-like fossil wood (Coniferales) in the Jurassic of western Liaoning and its evolutionary implications JIANG ZiKun1,3, WANG YongDong1*, ZHENG ShaoLin2,4, ZHANG Wu2 & TIAN Ning4 1 Nanjing Institute of Geology and Palaeontology, Chinese Academy of Sciences, Nanjing 210008, China; 2 Shenyang Center of China Geological Survey, Shenyang Institute of Geology and Mineral Resources, Shenyang 110034, China; 3 Graduate University of Chinese Academy of Sciences, Beijing 100049, China; 4 Institute of Palaeontology, Shenyang Normal University, Shenyang 110034, China Received July 5, 2011; accepted October 8, 2011; published online November 19, 2011 The genus Sciadopitys, containing a single species (S. verticillata), is the only extant representative of the Family Sciadopityaceae (Coniferales), and is a remarkable living fossil. Although some leafy fossils have been ascribed to Sciadopityaceae, fossil xylem material with a close affinity to this family is very rare, and there have been no fossils found showing both pith and primary xylem structures, which are of great importance for wood identification. Thus, it has been difficult to use fossils for the understanding of wood anatomy evolution in the sciadopityaceous plants over geological time. In this note we briefly report on Sciadopitys-like fossil wood found in the Middle Jurassic of western Liaoning, which bears well-preserved Protosciadopityoxylon-type secondary xylem, endarch primary xylem and heterogeneous pith. This is the first report of fossil specimens of the Sciadopityaceae with such detailed preservation of wood structures. The discovery provides precise anatomical evidence for reconstructing the evolu- tionary history and geographical distribution of Sciadopityaceae, as well as contributing to understanding of the fossil diversity of the Jurassic Yanliao Flora in northern China. -
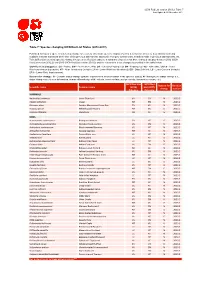
Table 7: Species Changing IUCN Red List Status (2012-2013)
IUCN Red List version 2013.2: Table 7 Last Updated: 25 November 2013 Table 7: Species changing IUCN Red List Status (2012-2013) Published listings of a species' status may change for a variety of reasons (genuine improvement or deterioration in status; new information being available that was not known at the time of the previous assessment; taxonomic changes; corrections to mistakes made in previous assessments, etc. To help Red List users interpret the changes between the Red List updates, a summary of species that have changed category between 2012 (IUCN Red List version 2012.2) and 2013 (IUCN Red List version 2013.2) and the reasons for these changes is provided in the table below. IUCN Red List Categories: EX - Extinct, EW - Extinct in the Wild, CR - Critically Endangered, EN - Endangered, VU - Vulnerable, LR/cd - Lower Risk/conservation dependent, NT - Near Threatened (includes LR/nt - Lower Risk/near threatened), DD - Data Deficient, LC - Least Concern (includes LR/lc - Lower Risk, least concern). Reasons for change: G - Genuine status change (genuine improvement or deterioration in the species' status); N - Non-genuine status change (i.e., status changes due to new information, improved knowledge of the criteria, incorrect data used previously, taxonomic revision, etc.) IUCN Red List IUCN Red Reason for Red List Scientific name Common name (2012) List (2013) change version Category Category MAMMALS Nycticebus javanicus Javan Slow Loris EN CR N 2013.2 Okapia johnstoni Okapi NT EN N 2013.2 Pteropus niger Greater Mascarene Flying -

Sciadopitys Verticillata: Japanese Umbrella-Pine1 Edward F
ENH-745 Sciadopitys verticillata: Japanese Umbrella-Pine1 Edward F. Gilman and Dennis G. Watson2 Introduction General Information This small tree is used for its unusual texture and growth Scientific name: Sciadopitys verticillata habit. The tree will grow very slowly to about 25 to 40 feet Pronunciation: sigh-uh-DOP-ih-tiss ver-tiss-ill-LAY-tuh tall (in 100 years) and spreads about 15 feet. On young Common name(s): Japanese umbrella-pine plants the branches stick straight out from the single, Family: Taxodiaceae straight trunk but become more pendulous with age. The USDA hardiness zones: 5A through 8A (Fig. 2) tree grows in a tight pyramid which can be utilized in a Origin: not native to North America rock garden or other small residential landscape site. The Invasive potential: little invasive potential effect is much like the ribs on an umbrella. Due to the Uses: specimen; container or planter unusual nature of the plant, people either love this tree or Availability: not native to North America won’t even look at it. Figure 2. Range Description Height: 25 to 30 feet Spread: 12 to 15 feet Figure 1. Mature Sciadopitys verticillata: Japanese umbrella-pine Crown uniformity: symmetrical Credits: Ed Gilman, UF/IFAS Crown shape: pyramidal 1. This document is ENH-745, one of a series of the Environmental Horticulture Department, UF/IFAS Extension. Original publication date November 1993. Revised December 2006. Reviewed February 2014. Visit the EDIS website at http://edis.ifas.ufl.edu. 2. Edward F. Gilman, professor, Environmental Horticulture Department; and Dennis G. Watson, former associate professor, Agricultural Engineering Department, UF/IFAS Extension, Gainesville, FL 32611. -

Master Plant List
MASTER PLANT LIST 5 7 8 6 Glasshouse 4 1 2 3 7 MASTER PLANT LIST PAGE 1 TREES 4 PAPERBARK MAPLE Acer griseum 2 3 RED WEEPING CUT-LEAF JAPANESE MAPLE Acer palmatum ‘Atropurpureum Dissectum’ 3 4 5 7 8 CORAL BARK JAPANESE MAPLE Acer palmatum ‘Sango Kaku’ 4 WEEPING CUT-LEAF JAPANESE MAPLE Acer palmatum ‘Viridis Dissectum’ 2 FULL MOON MAPLE Acer shirasawanum ‘Aureum’ 6 CELESTIAL DOGWOOD Cornus rutgersensis ‘Celestial’ 2 6 SANOMA DOVE TREE Davidia involucrata ‘Sonoma’ 4 SHAKEMASTER HONEY LOCUST Gleditsia triacanthos inermis ‘Shademaster’ 7 TEDDY BEAR MAGNOLIA Magnolia grandiflora ‘Teddy Bear’ 7 BRAKENS BROWN BEAUTY MAGNOLIA Magnolia grandiflora ‘Brackens Brown Beauty’ 2 JAPANESE STEWARTIA Stewartia pseudocamellia 7 WESTERN RED CEDAR Thuja plicata ‘Atrovirens’ SHRUBS 2 ROSANNIE JAPONICA ‘ROZANNIE’ Aucuba japonica ‘Rozannie’ 7 BARBERRY Berberis ‘William Penn’ 2 BEAUTY BERRY Callicarpa ‘Profusion’ 5 7 YULETIDE CAMELLIA Camellia sasanqua ‘Yuletide’ 5 QUINCE Chaenomeles ‘Dragon’s Blood’ 5 QUINCE Chaenomeles ‘Scarlet Storm’ 5 TWIG DOGWOOD WINTER FLAME DOGWOOD Cornus sanguinea ‘Arctic Fire’ 5 MIDWINTER FLAME DOGWOOD Cornus sericea ‘Midwinter Flame’ 1 HARRY LAUDER’S WALKING STICK Corylus avellana ‘Contorta’ 8 BEARBERRY Cotoneaster dammeri 7 SUMMER ICE CAUCASIAN DAPHNE Daphne caucasica ‘Summer Ice’ 2 LILAC DAPHNE Daphne genkwa 6 WINTER DAPHNE Daphne odora f. alba 3 4 CHINESE QUININE Dichroa febrifuga 2 RICE PAPER SHRUB Edgeworthia chrysantha 2 RICE PAPER SHRUB Edgeworhia chrysantha ‘Snow Cream’ 7 TREE IVY Fatshedera lizei 5 DWARF WITCH ALDER Fothergilla gardenii 5 JAPANESE WITCH HAZEL Hamamelis japonica ‘Shibamichi Red’ 2 4 6 BLUE BIRD HYDRANGEA Hydrangea macrophylla ssp. Serrata ‘Bluebird’ 3 4 BLUE DECKLE HYDRANGEA Hydrangea macrophylla ssp. -

Fluctuations in the East Asian Monsoon Over the Last 144Ka in the Northwest Pacific Based on a High-Resolution Pollen Title Analysis of IMAGES Core MD01-2421
Fluctuations in the East Asian monsoon over the last 144ka in the northwest Pacific based on a high-resolution pollen Title analysis of IMAGES core MD01-2421 Author(s) Igarashi, Yaeko; Oba, Tadamichi Quaternary Science Reviews, 25(13-14), 1447-1459 Citation https://doi.org/10.1016/j.quascirev.2005.11.011 Issue Date 2006-07 Doc URL http://hdl.handle.net/2115/14721 Type article (author version) File Information QSR25-13-14.pdf Instructions for use Hokkaido University Collection of Scholarly and Academic Papers : HUSCAP Fluctuations in the East Asian monsoon over the last 144 kyr in the northwest Pacific based on a high-resolution pollen analysis of IMAGES core MD01-2421 Yaeko Igarashia and Tadamichi Obab a Institute for Paleoenvironment of Northern Regions, Koyocho 3-7-5, Kitahiroshima, 061-1134, Japan Correspondence address: Institute for Paleoenvironment of Northern Regions, Koyocho 3-7-5, Kitahiroshima, 061-1134, Japan. Tel & Fax; 81-11-373-2938 e-mail; [email protected] b Graduate School of Environmental Earth Science, Hokkaido University Sapporo, 060-0810, Japan Present address: 2-2-3, Sendagaya, Shibuya-ku, Tokyo, 151-0051, Japan Abstract A high-resolution pollen analysis of IMAGES core MD01-2421 (45.83 m) from the northwest Pacific off central Japan was used to clarify the vegetation history of central Japan over the past 144 kyr. An age model was constructed using the oxygen 1 isotope stratigraphy of benthic foraminifera, 12 accelerator mass spectrometry (AMS) 14C datings, and two tephra layers with known eruption ages. The pollen temperature index Tp [= 100× Tw/(Tc + Tw), where Tw = sum of temperate taxa and Tc = sum of subalpine taxa] values were high during 129–119, 115–100, 82–76, 53–49, and 15–0 ka. -

(Cupressaceae: Cunninghamioideae), Anatomically Preserved Pollen Cones from the Eocene of Vancouver Island, British Columbia, Canada
Cunninghamia beardii sp. nov. (Cupressaceae: Cunninghamioideae), Anatomically Preserved Pollen Cones from the Eocene of Vancouver Island, British Columbia, Canada Buczkowski, E. L., Stockey, R. A., Atkinson, B. A., & Rothwell, G. W. (2016). Cunninghamia beardii sp. nov.(Cupressaceae: Cunninghamioideae), Anatomically Preserved Pollen Cones from the Eocene of Vancouver Island, British Columbia, Canada. International Journal of Plant Science, 177(1), 103-114. doi:10.1086/684106 10.1086/684106 University of Chicago Press Version of Record http://cdss.library.oregonstate.edu/sa-termsofuse Int. J. Plant Sci. 177(1):103–114. 2016. q 2015 by The University of Chicago. All rights reserved. 1058-5893/2016/17701-0009$15.00 DOI: 10.1086/684106 CUNNINGHAMIA BEARDII SP. NOV. (CUPRESSACEAE: CUNNINGHAMIOIDEAE), ANATOMICALLY PRESERVED POLLEN CONES FROM THE EOCENE OF VANCOUVER ISLAND, BRITISH COLUMBIA, CANADA Emma L. Buczkowski,* Ruth A. Stockey,1,* Brian A. Atkinson,* and Gar W. Rothwell*,† *Department of Botany and Plant Pathology, Oregon State University, Corvallis, Oregon 97331, USA; and †Department of Environmental and Plant Biology, Ohio University, Athens, Ohio 45701, USA Editor: Patricia G. Gensel Premise of research. A large pollen cone cluster attached to a cunninghamioid twig and surrounded by leaves has been identified from Eocene calcium carbonate marine concretions from the Appian Way locality on Vancouver Island, British Columbia, Canada. The cluster preserves 18 cones but probably bore at least 24 pollen cones based on cone placement in the cluster. Methodology. Specimens were studied using the cellulose acetate peel technique, and reconstructions were made with ImageJ visualization software. Pollen was examined using SEM. Pivotal results. Cones are helically arranged around the tip of an ultimate leafy branch that terminates in scale leaves, each showing a central resin canal. -

Master Plant List
MASTER PLANT LIST 5 N 9 7 8 6 Glasshouse 4 Green Roof 1 2 3 7 MASTER PLANT LIST PAGE 1 TREES 4 Acer griseum PAPERBARK MAPLE 2 3 Acer palmatum ‘Atropurpureum Dissectum’ RED WEEPING CUT-LEAF JAPANESE MAPLE 3 4 5 6 7 Acer palmatum ‘Sango Kaku’ CORAL BARK JAPANESE MAPLE 7 Chamaecyparis nootkatensis ‘Pendula’ WEEPING NOOTKA CYPRESS 7 Chamaecyparis obtusa ‘Gracilis’ SLENDER HINOKI CYPRESS 1 6 Cornus rutgersensis ‘Celestial’ CELESTIAL DOGWOOD 3 6 Davidia involucrata ‘Sonoma’ SONOMA DOVE TREE 4 Gleditsia triacanthos inermis ‘Shademaster’ SHADEMASTER HONEY LOCUST 7 Magnolia grandiflora ‘Teddy Bear’ TEDDY BEAR MAGNOLIA 7 Magnolia grandiflora ‘Bracken’s Brown Beauty’ BRAKEN’S BROWN BEAUTY MAGNOLIA 3 Picea pungens ‘Iseli Fastigiate’ ISELI FASTIGIATE SPRUCE 3 7 Sciadopitys verticillata ‘Wintergreen’ WINTERGREEN UMBRELLA PINE 2 3 Stewartia pseudocamellia JAPANESE STEWARTIA 7 Thuja plicata ‘Atrovirens’ WESTERN RED CEDAR SHRUBS 8 Arbutus compacta DWARF STRAWBERRY TREE 7 Aucuba japonica ‘Rozannie’ ROSANNIE AUCUBA 7 Berberis x gladwynensis ‘William Penn’ BARBERRY 5 Buxus microphylla ‘Wintergreen’ BOXWOOD 8 Callicarpa ‘Profusion’ BEAUTY BERRY 5 7 Camellia sasanqua ‘Yuletide’ YULETIDE CAMELLIA 3 Camellia sasanqua ‘Setsugekka’ SETSUGEKKA CAMELLIA 5 Chaenomeles ‘Dragon’s Blood’ QUINCE 5 Chaenomeles ‘Scarlet Storm’ QUINCE 5 Cornus sericea ‘Bud’s Yellow’ YELLOWTWIG DOGWOOD 1 Corylus avellana ‘Contorta’ HARRY LAUDER’S WALKING STICK 6 Cryptomeria japonica ‘Black Dragon’ BLACK DRAGON JAPANESE CEDAR 8 Cotoneaster dammeri BEARBERRY 2 Daphne genkwa LILAC DAPHNE 4 Dichroa febrifuga CHINESE QUININE 2 Edgeworthia chrysantha ‘Snow Cream’ RICE PAPER SHRUB 7 Fatshedera lizei TREE IVY 7 x Fatshedera lizei ‘Variegata’ VARIGATED TREE IVY 5 Fothergilla gardenii DWARF WITCH ALDER 5 Hamamelis japonica ‘Shibamichi Red’ JAPANESE WITCH HAZEL 2 4 Hydrangea macrophylla ssp.