An Analysis of a Demand Charge Electricity Grid Tariff in the Residential Sector
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Regional Kraftsystemutredning Møre Og Romsdal 2020 Hovedrapport
Regional kraftsystemutredning Møre og Romsdal 2020 Hovedrapport Mai 2020 Regional kraftsystemutredning for Møre og Romsdal 2020 Regional kraftsystemutredning Møre og Romsdal 2020 Istad Nett er av NVE tildelt utredningsansvaret for regionalnettet i Møre og Romsdal, og vil hvert annet år utarbeide en regional kraftsystemutredning for Møre og Romsdal, jf. Forskrift om energiutredninger. Formålet med utredningen er å vurdere mulig utvikling i behov for overføringskapasitet, skape en felles forståelse i samfunnet for endringer i kraftsystemet og gi grunnlag for behandling av søknader om konsesjon. Kraftsystemutredningen består av to dokumenter: Grunnlagsrapporten, som er underlagt taushetsplikt iht. kraftberedskapsforskriften §6-2, og er unntatt offentlighet i henhold til offentleglova § 13 første ledd. Hovedrapporten (dette dokumentet), som er et sammendrag av grunnlagsrapporten med vekt på informasjon av allmenn interesse. Hovedrapporten og en egen lysbildepresentasjon, som er gjengitt i kapittel 8 i hovedrapporten, er offentlig tilgjengelig på Istad Netts hjemmeside. Merknader: Etter ønske fra NVE er fylkesnavn fra 2019 benyttet i utredningen. Vi har forutsatt at dette ønsket også gjelder kommunenavn, ettersom en del underlagsinformasjon fra NVE til utredningen er oppgitt med kommuneinndeling fra 2019. Mulige virkninger av koronapandemien (covid-19) på last, forbruk, kraftpriser etc. er ikke vurdert eller hensyntatt i utredningen. Mai 2020 Forside: Bakgrunnsbilde: Vengedalen. T.R.Time, 2015. Rute1: Nyhamna landanlegg, en av eksisterende virksomheter innen kraftintensiv industri i Møre og Romsdal. Beskåret bilde fra beredskapsbrosjyre (AS Norske Shell), lastet 13.5.2020. Rute2: Illustrasjon fergelading, som er ett av flere bidrag til lastøkning innen alminnelig forsyning fra elektrifisering av transport. Beskåret bilde tatt ved Lote fergekai, med ladetårn til venstre. T.R.Time, 2015. -
Kart: NVE-Atlas
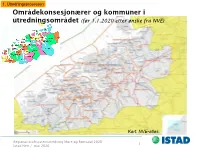
1. Utredningsprosessen Områdekonsesjonærer og kommuner i utredningsområdet (før 1.1.2020 etter ønske fra NVE) Kart: NVE-atlas. Regional kraftsystemutredning Møre og Romsdal 2020 1 Istad Nett / mai 2020 1. Utredningsprosessen Aktivitetsplan for to-årig syklus med regional kraftsystemutredning, med referanse til forskrift om energiutredninger. Regional kraftsystemutredning Møre og Romsdal 2020 2 Istad Nett / mai 2020 1. Utredningsprosessen Regional kraftsystemutredning Møre og Romsdal 2020 3 Istad Nett / mai 2020 3. Dagens kraftsystem Kraftproduksjon, historisk utvikling 1800 9 1600 8 1400 7 1200 6 1000 5 800 4 Effekt [MW] 600 Installert vintereffekt [MW] 3 400 Installert effekt [MW] 2 Middelproduksjon [TWh/år] [TWh/år] Middelproduksjon 200 1 0 0 1950 1955 1960 1965 1970 1975 1980 1985 1990 1995 2000 2005 2010 2015 2020 Tilgjengelig vintereffekt Installert effekt Middelproduksjon [MW] [MW] [TWh] Vannkraft 1237 1576 6.92 Vindkraft 76 154 0.37 Varmekraft 27 27 0.19 Total 1339 1757 7.48 Regional kraftsystemutredning Møre og Romsdal 2020 4 Istad Nett / mai 2020 3. Dagens kraftsystem Last og forbruk 4 % 2 % 6 % Ind. med eldrevne pros. 14.0 6 % Husholdning 12.0 Industri 10.0 17 % Handel og tjenester 65 % 8.0 Offentlig 6.0 Jordbruk 4.0 Totalt årsforbruk i 2019: 12.6 TWh 2.0 Målt årosforbruk årosforbruk Målt [TWh] 0.0 1996 2001 2006 2011 2016 Alminnelig forsyning KII Alminnelig forsyning med temperaturkorrigeringer Total, temp.korr. Last Vekstrate 0.86 Forbruk Vekstrate (%): 0.97 1050 10 år 4.8 Temperatur- korrigert total 1000 Prioritert, 4.6 temp.korr. 10 år 950 4.4 Målt total Prioritert, 900 4.2 850 temp.korr. -

Maria Sandsmark 2008:12
Maria Sandsmark A regional energy paradox - the case of Central Norway 2008:12 Maria Sandsmark A regional energy paradox - the case of Central Norway Arbeidsnotat / Working Paper 2008:12 Høgskolen i Molde / Molde University College Molde, november / November 2008 ISSN 1501-4592 ISBN-13 978-82-7962-107-2 A regional energy paradox – the case of Central Norway* Maria Sandsmark Molde Research Institute, Britveien 4, N-6411 Molde, Norway Tel: +47 71 21 42 84, Fax: +47 71 21 42 99 E-mail: [email protected] Abstract Central Norway is expected to have a gap of 8 TWh in 2010 because of heavy investments in electricity intensive industry. The region has two landing sites for natural gas and a considerable potential for wind power to cover the gap. Small-scale hydropower and upgrading of existing hydropower plants also constitute a regional energy potential. Paradoxically, the most realistic investment prospect seems to be extensive investments in new transmission lines to cover the electricity deficit. The aim of this paper is to present a problem of regional supply security and public intervention and discuss possible directions for improving regulators’ practical authorisation tools. Key words: Regional electricity market; Supply security; Investment; Regulatory risk JEL Classification: L11; L51; L94 * Financial support from the Business and Management Research Fund in Mid-Norway is gratefully acknowledged. 1. Introduction In theory, deregulated electricity markets should provide appropriate investment incentives to market participants. However, in practice the expected gains from restructuring processes are often restrained by market imperfections and the vagaries of nature and politics, c.f. -

Istad AS Samfunnsrapport 2015 - 2018 for Istad-Konsernet
Istad AS Samfunnsrapport 2015 - 2018 for Istad-konsernet Dato: 15.05.2019 www.asplanviak.no Dokumentinformasjon Oppdragsgiver: Istad AS Tittel på rapport: Samfunnsrapport 2015 - 2018 for Istad-konsernet Oppdragsnavn: Samfunnsregnskap Istad Utarbeide utredning Oppdragsnummer: 621232-01 Utarbeidet av: Sven Haugberg Oppdragsleder: Sven Haugberg Tilgjengelighet: Åpen Kort sammendrag I denne rapporten vises hvilken samfunnsmessig betydning Istad-selskapenes økonomiske aktivitet har – lokalt og nasjonalt. Konsernets verdiskaping, vare- og tjenestekjøp, sysselsetting og overføringer til andre – særlig til offentlig sektor. 01 15.05.19 Samfunnsrapport 2015 - 2018 for Istad-konsernet sh VERSJON DATO BESKRIVELSE UTARBEIDET AV KS Forord Istad-konsernet har kontor i Molde og virksomheten er basert på nettvirksomhet, kraftproduksjon, kraftomsetning, fjernvarme og fibervirksomhet. Det har vært ønskelig å vise hvilken samfunnsmessig betydning Istad-selskapenes økonomiske aktivitet har – lokalt og nasjonalt. I denne rapporten vises konsernets verdiskaping, vare- og tjenestekjøp, sysselsetting og overføringer til andre – særlig til offentlig sektor. Arbeidet er utført av Sven Haugberg. Dataene er i hovedsak skaffet til veie av økonomisjef Bente Holberg i Istad. Stavanger, 15.05.2019 Sven Haugberg Oppdragsleder side 2 av 12 Innhold 1. INNLEDNING .............................................................................................................. 4 2. SAMFUNNSREGNSKAPET........................................................................................... -

Fylkesros Møre Og Romsdal Var Sist Revidert I 2017
FylkesROS Møre og Romsdal 1 FylkesROS Møre og Romsdal FORORD Denne rapporten er første versjon av FylkesROS Møre og Romsdal, og er utarbeidd i fellesskap av Møre og Romsdal Fylkeskommune og Fylkesmannen i Møre og Romsdal i perioden 2011 – 2016. Fylkeskommunen og Fylkesmannen har utarbeidd felles risiko- og sårbarheitsanalysar sidan 2004 for Møre og Romsdal. FylkesROS-sjø vart ferdigstilt i 2007, og FylkesROS-fjellskred kom i 2011. Like etter starta arbeidet med ein heilskapleg risiko- og sårbarheitsanalyse for fylket. FylkesROS Møre og Romsdal er hovudsakleg ein sårbarheitsanalyse med fokus på å avdekke sårbarheiter i samfunnet. Målet er å gje eit bilete av kor godt rusta vi som samfunn er til å takle konsekvensane av uønskte hendingar. Vi har våre utfordringar i Møre og Romsdal. Vi bur i eit fylke med mykje topografi og mykje vêr. Landskap, natur og klima er variert og spenner frå kyst- og øykommunar, til fjord- og innlandskommunar. Møre og Romsdal har ei spesiell utfordring med risiko for fleire store fjellskred. Denne risikoen sett store krav til beredskapen lokalt, regionalt og nasjonalt. Samhandling og beredskap har blitt styrka gjennom beredskapsplanlegging og handtering av uønskte hendingar. Fylkesmannen opplev at fylket er godt budd på å takle utfordringane som oppstår. Likevel kan vi alltid bli betre. I den samanheng er FylkesROS eit verktøy som bidreg til å identifisere utfordringar og prioritere vidare arbeid. Nokre av dei største hendingane i regionen i nyare tid er ekstremvêrhendingar med nyttårsorkanen i 1992, orkanen «Dagmar» 1. juledag 2011 og orkanen «Tor» i januar 2016. Dette er hendingar som har prega fylket, og som har hatt stor påverknad på arbeidet med samfunnstryggleik og beredskap. -

Gjemnesnytt (.PDF, 8
NR. 8 • desember 2017 Nytt INFORMASJONSBLAD FOR GJEMNES JULEHELSING FRÅ ORDFØRAREN Gode tilbud året rundt! Gjemnes Kommunen har dei Det er siste åra hatt ei positiv Nærhet til vi som folketalsutvikling. kundene er postkontoret Stort utvalg av Tredje kvartal i 2017 Spennende hadde vi ein auke strikkegarn i utvalg fra lokale flotte farger leverandører Gjemnes i folketalet på 22 personar, noko som Coop Marked Batnfjord kommune var det beste resultat i 6631 Batnfjordsøra • Tel. 979 94 970 Man – fredag 08.00 – 21.00 • Lørdag 09.00 - 19.00 heile fylket. Folketalet Ordfører Knut Sjømæling er viktig for nivået på dei framtidige statlege overføringane. Tilrettelegging av tomteområde rundt om i heile kommunen BOKKVELD I GJEMNES SakeR til kommuNeStyRemøte 12.12 blir eit satsingsområde for å legge til kl. 16.00 i kommuNeStyReSaleN rette for nyetablering når «nysjukehuset» på Hjelset står ferdig. Heile kommunen Sakliste: kan by på attraktive tomter, og framifråe • Godkjenning av møtebok fra forrige kvalitetar i nærmiljøet, som gjev grunn møte til å busetja seg i kommunen vår. Det er ønskjeleg at den enkelte «framsnakkar» • Høringsuttalelser økonomiplan desse kvalitetane, og det vi elles har å 2018-2021. Årsbudsjett 2018 by på. Stor takk til alle dei frivillige som • Astaddalen museums- og frilufts- nettopp legg til rette for dette på ulikt barnehage - sluttføring av 2. etasje vis året rundt. Mange harde julegaver i år? Les mer side 10 • Økonomiplan og handlingsprogram Vi har dei siste to åra teke imot 23 flykt- 2018-2021. Budsjett ningar (19 menn, 3 kvinner og 4 barn). bjeRkely 4H 60 åRS-jubileum Vi har ei god vaksenopplæring med • Framtidig organisering av PPT i engasjerte lærarar. -

Kraftsystemutredning for Møre Og Romsdal, Hovedrapport
Hovedrapport KRAFTSYSTEMUTREDNING MØRE OG ROMSDAL 2018 Mai 2018 Kraftsystemutredning for Møre og Romsdal 2018 INNHOLDSFORTEGNELSE 1 BESKRIVELSE AV UTREDNINGSPROSESSEN ....................................................................... 7 1.1 UTREDNINGSOMRÅDET OG DELTAKERE I UTREDNINGSPROSESSEN ................................................. 7 1.2 SAMORDNING MED TILGRENSENDE UTREDNINGSOMRÅDER ............................................................ 7 1.3 SAMORDNING MOT ANDRE KOMMUNALE OG FYLKESKOMMUNALE PLANER .................................... 7 2 FORUTSETNINGER I UTREDNINGSARBEIDET .................................................................... 7 2.1 MÅL FOR DET FRAMTIDIGE KRAFTSYSTEMET .................................................................................. 7 2.2 AMBISJONSNIVÅ OG TIDSHORISONT ................................................................................................ 7 2.3 TEKNISKE OG ØKONOMISKE VURDERINGER .................................................................................... 8 3 BESKRIVELSE AV DAGENS KRAFTSYSTEM ......................................................................... 8 3.1 STATISTIKK FOR KRAFTPRODUKSJON .............................................................................................. 8 3.2 STATISTIKK FOR ELEKTRISITETSFORBRUK ...................................................................................... 8 3.3 KRAFTBALANSE ............................................................................................................................. -

2012Årsrapport
ÅRSRAPPORT 2012 INNHOLD 04 STYRET 28 REVISORS BERETNING 05 NØKKELTALL 31 KONSERNSJEFENS KOMMENTARER 06 ÅRSBERETNING 32 DETTE ER ISTAD 13 RESULTATREGNSKAP 33 ORGANISASJONEN 14 BALANSE 34 DATTERSELSKAPENE 16 KONTANTSTRØMANALYSE 38 ENGLISH SUMMARY 17 NOTER 2 ISTAD ÅRSRAPPORT 2012 Gjennom Istadfondet støtter Istad idrett og kultur i Molde, Midsund, Aukra, Fræna, Eide og Gjemnes. For mottakerne utgjør disse pengene en stor forskjell. 3 STYRET TORGEIR DAHL T HOMAS SANDBERG GEIRAN KRISTIN STEENFELDT-FOSS FRANK OVE SÆTHER L EIF ARNE LANGØY JAN PETTER HAMMERØ A LF TERJE ULLEBØ JARLE RISNES TERJE HELLUM KRISTOFFER SLETTEN O BSERVATØRER Styret består av 8 medlemmer, og av disse velges 2 av og blant de ansatte. I tillegg har de ansatte to observatører med tale- og forslags- rett. Styret har denne sammensetning, med varamedlemmene for de ansattvalgte representantene rangert i nummerorden: Styremedlemmer: Varamedlemmer: Torgeir Dahl – styreleder Ole Petter Meijer Moldekraft AS Thomas Sandberg Geiran – nestleder Henning Villanger Trondheim Energi AS Kristin Steenfeldt-Foss Kathinka Rudlang Trondheim Energi AS Frank Ove Sæther Olbjørn Kvernberg Molde kommune Leif Arne Langøy Svein Håkon Ranvik Moldekraft AS Jan Petter Hammerø Toril Hovdenak Molde kommune Alf Terje Ullebø Ansattvalgt styremedlem Jarle Risnes Ansattvalgt styremedlem Observatører: Terje Hellum Ansattvalgt observatør Kristoffer Sletten Ansattvalgt observatør Varamedlemmer for Ullebø og Hellum: Varamedlemmer for Risnes og Sletten: 1. Wenche Hild Sandnes 1. Frank Hagen 2. Stig Arseth 2. Kristin -

Norwegian Bergen Hosts World Cycling Championships American Story on Page 8 Volume 128, #19 • October 6, 2017 Est
the Inside this issue: NORWEGIAN Bergen hosts World Cycling Championships american story on page 8 Volume 128, #19 • October 6, 2017 Est. May 17, 1889 • Formerly Norwegian American Weekly, Western Viking & Nordisk Tidende $3 USD Who were the Vikings? As science proves that some ancient warriors assumed to be men were actually women, Ted Birkedal provides an overview of historical evidence for real-life Lagerthas WHAT’S INSIDE? « Den sanne oppdagelsesreise Nyheter / News 2-3 TERJE BIRKEDAL består ikke i å finne nye Business 4-5 Anchorage, Alaska landskaper, men å se med Opinion 6-7 In the late 19th century a high-status Viking-era were buried with a sword, an axe, a spear, arrows, and nye øyne. » Sports 8-9 grave was excavated at Birka, Sweden. The grave goods a shield. The woman from Solør was also buried with a – Marcel Proust Research & Science 10 included a sword, an axe, a spear, a battle knife, several horse with a fine bridle. Another grave from Kaupang, armor-piercing arrows, and the remains of two shields. Norway, contained a woman seated in a small boat with Norwegian Heritage 11 Two horses were also buried with the grave’s inhabitant. an axe and a shield boss. Still another high-status grave Taste of Norway 12-13 Until 2014 the grave was thought to belong to a in Rogaland, Norway, turned up a woman with a sword Norway near you 14-15 man, but a forensic study of the skeleton in 2014 sug- at her side. Many other graves throughout Scandinavia Travel 16-17 gested that the buried person was a woman. -

Energisk Til Stede 1 INNHOLD ISTAD – Energisk Til Stede!
ÅRSRAPPORT 2003 Energisk til stede 1 INNHOLD ISTAD – energisk til stede! Styret........................................................... 4 Istad konsernets visjon er å være en lønnsom lokal drivkraft. Bak en slik visjon ligger det blant annet at man som en av de større Nøkkeltall ................................................... 5 bedriftene i regionen ønsker å være med på å gi noe tilbake til Årsberetning ............................................6-10 lokalsamfunnet. Istad støtter derfor en rekke kulturinstitusjone som vi mener har stor betydning for regionen vår. I denne årsrappor- Resultatregnskap ..........................................12 ten er noen av disse representert ved Molde Fotball, Teatret Vårt, Balanse ......................................................13 Moldejazz og Bjørnsonfestivalen. Kontantstrømanalyse ...................................14 I tillegg til dette ønsker Istad å gi sponsormidler til organisasjoner Noter.....................................................15-24 eller prosjekter som bidrar positivt for barn og unge i lokalmiljøet, og dermed stimulere disse til videre arbeid. Denne støtten er Revisors beretning....................................... 25 organisert under ISTADFONDET. ISTADFONDET tildeler midler Adm. direktørs kommentarer ........................ 26 etter søknad to ganger i året. Ved siste tildeling mottok man over 120 søknader, og 47 lag og organisasjoner ble tildelt midler fra Dette er Istad.............................................. 27 fondet. I årsrapporten presenterer vi kort -

Romsdalskonferansen 2018
Med Jan Erik Nyland, Julie Brodtkorb, Kolbjørn Stølen, Nils Apeland, Nina Jensen, Olav Thon, Jan Solid Storehaug, Stein Lier-Hansen, Tom Samuelsen, Tone Sofie Aglen, Øystein Bache og Rune Gokstad. Molde, 27. september 2018 Kolbjørn Heggdal Lina Jenset Hjelset Kaare Jakob Hasselø Otto Nygård [email protected] [email protected] [email protected] [email protected] Tlf: 915 89 768 Tlf: 980 00 606 Tlf: 957 34 401 Tlf: 958 87 639 Stig Feragen Marianne Wirum Granum Eirik Berg Sponås Håvard Ulvestad [email protected] [email protected] [email protected] [email protected] Tlf: 995 61 030 Tlf: 915 22 652 Tlf: 481 04 362 Tlf: 932 00 996 ENGASJERT BANK En bank som vil bety noe for næringslivet i Møre og Romsdal må by på mer enn bare penger. Engasjerte og kompetente medarbeidere som kjenner og forstår de lokale forholdene, gir de beste rådene. Ta kontakt for en uforpliktende samtale. VELKOMMEN VELKOMMEN TIL ROMSDALSKONFERANSEN 2018 Vi har igjen gleden av å invitere til Romsdalskonferansen! Den trettende i rekken. Kolbjørn Heggdal Lina Jenset Hjelset Kaare Jakob Hasselø Otto Nygård Årets tema er reformer i samfunns- og næringsliv, nye forretningsmodeller, omstilling, bærekraft og kommu- [email protected] [email protected] [email protected] [email protected] nikasjon i (bred forstand). Også til årets konferanse har vi fått med en rekke dagsaktuelle, spissformulerte og Tlf: 915 89 768 Tlf: 980 00 606 Tlf: 957 34 401 Tlf: 958 87 639 sentrale personer, fra næringsliv og samfunnsliv for å belyse temaet: Stein Lier Hansen er markant talsperson for industrien i Norge som administrerende direktør i Norsk Industri. -

Midsund Kommune Reguleringsplan for 63/13 - Rakvåg Fråsegn Til Varsel Om Oppstart
Vår dato: Vår ref: 30.08.2019 2019/3989 Dykkar dato: Dykkar ref: 11.07.2019 HARALD HJELLE ARKITEKTER AS Saksbehandlar, innvalstelefon Postboks 100 71 25 84 33, Kristin Eide 6282 BRATTVÅG Midsund kommune Reguleringsplan for 63/13 - Rakvåg Fråsegn til varsel om oppstart Fylkesmannen er statens representant i fylket og har fleire roller og oppgåver innan planlegging etter plan- og bygningslova. Ei viktig oppgåve for Fylkesmannen i kommunale planprosessar er å sjå til at nasjonale og viktige regionale omsyn blir ivaretatt i planarbeidet. Fagområde som miljøvern, landbruk, helse, oppvekst og samfunnstryggleik står sentralt. I tillegg skal Fylkesmannen sikre at kommunale vedtak i plan- og byggesaker er i samsvar med gjeldande lovverk. Bakgrunn Fylkesmannen har mottatt melding om oppstart av planarbeid for å legge til rette for 20-25 bustader i eit område satt av til LNF-formål i kommuneplanen. Fylkesmannen har ut frå sine ansvarsområde følgande merknader: Natur- og miljøvern Kjerringvatnet naturreservat ligg nær planområdet. Byggegrense kring vatnet er satt til 50 meter i kommuneplanen. Vi rår til at tilrettelegging for bustader i planområdet både direkte og indirekte tar omsyn til naturreservatet. Vi viser her til eiga verneforskrift for reservatet. Samordna bustad-, areal- og transportplanlegging – klima Planområdet ligg 3 km unna sentrum og barneskulen, og 5 km unna ungdomsskulen. Avstanden tilseier at barn og unge i mindre grad vil nytte sykkel eller gå til skulen. Dette blir forsterka ved at det ikkje er gang- og sykkelveg langs Utsidevegen som kan gi trygg skuleveg. Å legge til rette for bustader på Rakvåg vil truleg ikkje bidra til at auken i transport blir tatt med sykkel og gange, og dette bør planen vurdere verknadane av både for barn og unge/folkehelse og for klima.