DOCSLIB.ORG

Astronomy at High Angular Resolution

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Astronomy at High Angular Resolution Astronomical News Report on the ESO Workshop Astronomy at High Angular Resolution held at ESO Headquarters, Garching, Germany, 24–28 November 2014 Henri Boffin1 Linda Schmidtobreick1 Gaitee Hussain1 Jean-Philippe Berger1 1 ESO A workshop took place in Brussels in 2000 on astrotomography, a generic term for indirect mapping techniques that can be applied to a huge variety of astrophysical systems, ranging from planets, single stars and binaries to active galactic nuclei. It appeared to be timely to revisit the topic given the many past, recent and forthcoming improvements in telescopes and instru- mentation. We therefore decided to repeat the astrotomography workshop, Figure 1. Photograph of the participants at the work- but to put it into the much broader con- shop in the entrance hall at ESO Headquarters. text of high angular resolution astron- omy. Many techniques, from lucky and – single-dish tomographic reconstruction telescope in La Silla (Merkle et al., 1989). speckle imaging, adaptive optics to methods (astrotomography), with AO is now part of many systems at the interferometry, are now widely employed microarcsecond resolution, but appli- Paranal Observatory, as well as in all to achieve high angular resolution and cable only to certain classes of objects. major observatories, and has led to many they have led to an amazing number of the most important ESO discoveries: of new discoveries. A summary of the The workshop was structured to present the supermassive black hole at the centre workshop themes is presented. the various techniques, with extensive of the Milky Way, the first image of an reviews, and then to consider the various exoplanet and imaging of the young discs scientific fields that have profited from around stars. AO comes in many differ- The workshop brought together people these techniques: exoplanets and brown ent flavours and can be defined by the from different communities (see the con- dwarfs, stars, binaries, and large-scale total corrected field of view versus the ference photograph, Figure 1), who use phenomena. We give a very short sum- Strehl ratio which the system achieves. various techniques to construct images at mary of the material presented; the pro- These flavours include ground-layer AO very high angular resolution, with the aim gramme of the workshop is available1 and (GLAO), multi-conjugated AO (MCAO) and of reviewing these methods, the progress the presentations can be downloaded2. eXtreme AO (XAO). All major telescopes in the field, the new harvest of results that have second generation AO instruments have been collected, as well as to pre- currently in operation, which can reach pare the next generation of astronomers Beating the seeing: Reaching the typically 15–50 milliarcsecond (mas) res- to use these tools and techniques. The diffraction limit olution with high Strehl ratios and have various techniques used to beat the ten times more actuators than the first seeing and the telescope diffraction limit Atmospheric turbulence creates inhomo- generation AO systems. can be roughly distributed as follows: geneities in the refractive index of air that – single-dish imaging methods have affects the image quality — the infamous At the Very Large Telescope (VLT), the been developed to beat the seeing at “seeing”. To counter this, astronomers second generation AO system is SPHERE the focus of telescopes (e,g., adaptive have devised a series of techniques, such (an XAO system), which is beginning reg- optics, lucky/speckle/holographic as lucky imaging, speckle imaging and ular operations (see article on Science imaging, sparse aperture masking) adaptive optics. Verification by Leibundgut et al., p. 2) and aiming at sub-arcsecond spatial reso- is based on a system with 1600 actuators lution up to the diffraction limit of single Adaptive optics (AO), which has a long (see the result in Figure 2, right). A GLAO telescopes; history at ESO, aims at neutralising the system (part of the VLT Adaptive Optics – techniques that allow the diffraction atmospheric turbulence by a closed-loop Facility [AOF]) is under development at limit to be beaten in order to achieve system. As Julien Milli reminded us in ESO to assist instruments such as MUSE milliarcsecond angular resolution using his presentation, the first astronomical and Hawk-I, combining diffraction-limit direct (optical interferometry) and system ever online was Come-On at the imaging and relatively wide-field imaging indirect (e.g., spectro-astrometry) tech- Observatoire de Haute-Provence, which spectroscopy. Not least, the whole niques; and later became operational at the 3.6-metre concept of the European Extremely Large 52 The Messenger 159 – March 2015 Figure 2. Showing the NaCo L: sented in detail by Mike Ireland. In par- N progress achieved in ticular, he pointed out that there are AO: a comparative study of the disc around HR some moderate to high Strehl regimes, E 4796 A by NACO (left; where working in the Fourier plane using from Milli et al., 2014) a non-redundant mask offers improved and, more recently, with performance over standard pupil-plane SPHERE (right; from Milli et al. [2015] in prep.). analysis; the example of a putative form- ing planet in a young disc in LkCa 15 was discussed. As a complement, Makoto Uemura showed how sparse aperture N modelling can be applied, in a cross- disciplinary approach, to Very Long 1 arcsec 1 arcsec E Baseline Imaging (VLBI) images, Doppler –16 –11 –5.8–0.7 4.4 9.5 15 20 25 30 35 tomography and gamma-ray Compton imaging. In another vein, Jaeho Choi presented a non-interferometric phase- Telescope (E-ELT) requires the use of that, at the 5-metre Palomar telescope, differential imaging method that uses AO. The future lies also in the develop- AO and lucky imaging are combined, Foucault knife-edge filtering. ment of wide-field AO systems (WFAO), leading to the highest resolution image as shown by Benoît Neichel in his talk. ever taken in the visible on faint targets, By using multiple laser guide stars (LGS), with a resolution of 35 mas in the I-band Beating the diffraction limit: WFAO significantly increases the field and a Strehl ratio of 17 %. Gergely The milliarcsecond horizon of view of AO-corrected images. The first Csépány combined lucky imaging and AO such system in routine operation is GeMS, to study a sample of 38 T Tauri mul tiple In order to reach higher spatial resolu- the Gemini Multi-Conjugate AO System, systems over a 20-year period, and was tions, different techniques, such as long- which uses five LGS and provides 87 by able to cover the orbits in several of them. baseline interferometry where two or 87 arcsecond AO-corrected images in In addition, Mackay presented a proposal more telescopes are combined to obtain the H-band with a resolution of 80 mas. for a mosaic of lucky imagers for the fringes, are required. The technique was Such wide-field images with uniform NTT. This project, called GravityCam, will reviewed by Jean-Baptiste LeBouquin. point-spread functions over the full field consist of no less than 100 CCDs with The contrast (“visibility”) and phase infor- of view are particularly useful for astro- 70 mas pixels and will mainly be used for mation (“closure” or “differential phases”) metric studies, for example in clusters or exoplanet microlensing surveys, down to of the interference fringe packets can at the Centre of the Milky Way. Moreover, below an Earth mass. be used to retrieve direct information on such developments are critical, as all the the observed object brightness distri- ELTs rely on multi-LGS WFAO systems. Speckle imaging was introduced by bution. While the technique has been in Sridharan Rengaswamy, who showed the widespread use in the radio domain for Wolfgang Brandner reviewed lucky advantages of the method and its signifi- several decades, it is now also becoming imaging, which is often presented as a cant contribution to the imaging of binary a routine technique in the optical domain, poor man’s adaptive optics. It exploits stars. More details about this technique in particular at the VLT Interferometer moments of good seeing, that is, it takes is given in Rengaswamy et al. (2014). (VLTI) where the angular resolution in the many short exposures and then retains This technique was further developed, as near-infrared is of the order of a few milli- only those images that have the best speckle holography, by Rainer Schödel, arcseconds. quality (typically 10 % of the whole). The which he calls “lucky imaging on steroids” technique is still quite popular and new to reconstruct images of crowded and Two regimes of data analysis were pre- projects are being devised, especially “wide” fields of view of several tens of sented. In the first, the measurements since the availability of noise-free detec- arcseconds, while keeping the instrument are fitted with a parametric model of the tors such as L3 (Low Light Level, LLL) sensitivity. object. This is particularly well suited and extended multiplication (EM) charge when the number of measurements is coupled devices (CCDs), and the fact In sparse aperture masking (SAM; or limited, the object structure is well under- that these systems are quite affordable. non-redundant masking [NRM] depend- stood or the object is only marginally For example, the AstroLux Sur on the ing on which side of the Atlantic you resolved. This was, and still is, the bread ESO New Technology Telescope (NTT) work), a mask with a few holes is placed and butter of interferometry and is had a total hardware cost of only 50 000 in front of the AO system. This trans- applied to the measurement of precise euros. Lucky imaging is also quite useful forms the primary mirror into a separate- diameters, binary parameters or simple as it generally has fainter limiting magni- element, multiple-aperture interferometer morphological parameters; it is well tudes than most AO systems, and it can and allows diffraction-limited imaging illustrated by the spectacular case of the work in the visible where AO is not so of (bright) astrophysical targets to be expansion of a nova shell (Schaeffer et developed.
Load more

Recommended publications
  • Journal of Interdisciplinary Science Topics Determining Distance Or
    Journal of Interdisciplinary Science Topics Determining Distance or Object Size from a Photograph Chuqiao Huang The Centre for Interdisciplinary Science, University of Leicester 19/02/2014 Abstract The purpose of this paper is to create an equation relating the distance and width of an object in a photograph to a constant when the conditions under which the photograph was taken are known. These conditions are the sensor size of the camera and the resolution and focal length of the picture. The paper will highlight when such an equation would be an accurate prediction of reality, and will conclude with an example calculation. Introduction may be expressed as a tan (opposite/adjacent) In addition to displaying visual information relationship: such as colour, texture, and shape, a photograph (1.0) may provide size and distance information on (1.1) subjects. The purpose of this paper is to develop such an equation from basic trigonometric principles when given certain parameters about the photo. Picture Angular Resolution With the image dimensions, we can make an Picture Field of View equation for one-dimensional angular resolution. First, we will determine an equation for the Since l2 describes sensor width and not height, we horizontal field of view of a photograph when given will calculate horizontal instead of vertical angular the focal length and width of the sensor. resolution: Consider the top down view of the camera (2.0) system below (figure 1), consisting of an object (left), lens (centre), and sensor (right). Let d be the (2.1) 1 distance of object to the lens, d2 be the focal length, Here, αhPixel is the average horizontal field of l1 be the width of the object, l2 be the width of the view for a single pixel, and nhPixel is the number of sensor, and α be the horizontal field of view of the pixels that make up a row of the picture.
    [Show full text]
  • Sub-Airy Disk Angular Resolution with High Dynamic Range in the Near-Infrared A
    EPJ Web of Conferences 16, 03002 (2011) DOI: 10.1051/epjconf/20111603002 C Owned by the authors, published by EDP Sciences, 2011 Sub-Airy disk angular resolution with high dynamic range in the near-infrared A. Richichi European Southern Observatory,Karl-Schwarzschildstr. 2, 85748 Garching, Germany Abstract. Lunar occultations (LO) are a simple and effective high angular resolution method, with minimum requirements in instrumentation and telescope time. They rely on the analysis of the diffraction fringes created by the lunar limb. The diffraction phenomen occurs in space, and as a result LO are highly insensitive to most of the degrading effects that limit the performance of traditional single telescope and long-baseline interferometric techniques used for direct detection of faint, close companions to bright stars. We present very recent results obtained with the technique of lunar occultations in the near-IR, showing the detection of companions with very high dynamic range as close as few milliarcseconds to the primary star. We discuss the potential improvements that could be made, to increase further the current performance. Of course, LO are fixed-time events applicable only to sources which happen to lie on the Moon’s apparent orbit. However, with the continuously increasing numbers of potential exoplanets and brown dwarfs beign discovered, the frequency of such events is not negligible. I will list some of the most favorable potential LO in the near future, to be observed from major observatories. 1. THE METHOD The geometry of a lunar occultation (LO) event is sketched in Figure 1. The lunar limb acts as a straight diffracting edge, moving across the source with an angular speed that is the product of the lunar motion vector VM and the cosine of the contact angle CA.
    [Show full text]
  • The Most Important Equation in Astronomy! 50
    The Most Important Equation in Astronomy! 50 There are many equations that astronomers use L to describe the physical world, but none is more R 1.22 important and fundamental to the research that we = conduct than the one to the left! You cannot design a D telescope, or a satellite sensor, without paying attention to the relationship that it describes. In optics, the best focused spot of light that a perfect lens with a circular aperture can make, limited by the diffraction of light. The diffraction pattern has a bright region in the center called the Airy Disk. The diameter of the Airy Disk is related to the wavelength of the illuminating light, L, and the size of the circular aperture (mirror, lens), given by D. When L and D are expressed in the same units (e.g. centimeters, meters), R will be in units of angular measure called radians ( 1 radian = 57.3 degrees). You cannot see details with your eye, with a camera, or with a telescope, that are smaller than the Airy Disk size for your particular optical system. The formula also says that larger telescopes (making D bigger) allow you to see much finer details. For example, compare the top image of the Apollo-15 landing area taken by the Japanese Kaguya Satellite (10 meters/pixel at 100 km orbit elevation: aperture = about 15cm ) with the lower image taken by the LRO satellite (0.5 meters/pixel at a 50km orbit elevation: aperture = ). The Apollo-15 Lunar Module (LM) can be seen by its 'horizontal shadow' near the center of the image.
    [Show full text]
  • Understanding Resolution Diffraction and the Airy Disk, Dawes Limit & Rayleigh Criterion by Ed Zarenski [email protected]
    Understanding Resolution Diffraction and The Airy Disk, Dawes Limit & Rayleigh Criterion by Ed Zarenski [email protected] These explanations of terms are based on my understanding and application of published data and measurement criteria with specific notation from the credited sources. Noted paragraphs are not necessarily quoted but may be summarized directly from the source stated. All information if not noted from a specific source is mine. I have attempted to be as clear and accurate as possible in my presentation of all the data and applications put forth here. Although this article utilizes much information from the sources noted, it represents my opinion and my understanding of optical theory. Any errors are mine. Comments and discussion are welcome. Clear Skies, and if not, Cloudy Nights. EdZ November 2003, Introduction: Diffraction and Resolution Common Diffraction Limit Criteria The Airy Disk Understanding Rayleigh and Dawes Limits Seeing a Black Space Between Components Affects of Magnitude and Color Affects of Central Obstruction Affect of Exit Pupil on Resolution Resolving Power Resolving Power in Extended Objects Extended Object Resolution Criteria Diffraction Fringes Interfere with Resolution Magnification is Necessary to See Acuity Determines Magnification Summary / Conclusions Credits 1 Introduction: Diffraction and Resolution All lenses or mirrors cause diffraction of light. Assuming a circular aperture, the image of a point source formed by the lens shows a small disk of light surrounded by a number of alternating dark and bright rings. This is known as the diffraction pattern or the Airy pattern. At the center of this pattern is the Airy disk. As the diameter of the aperture increases, the size of the Airy disk decreases.
    [Show full text]
  • Computation and Validation of Two-Dimensional PSF Simulation
    Computation and validation of two-dimensional PSF simulation based on physical optics K. Tayabaly1,2, D. Spiga1, G. Sironi1, R.Canestrari1, M.Lavagna2, G. Pareschi1 1 INAF/Brera Astronomical Observatory, Via Bianchi 46, 23807 Merate, Italy 2 Politecnico di Milano, Via La Masa 1, 20156 Milano, Italy ABSTRACT The Point Spread Function (PSF) is a key figure of merit for specifying the angular resolution of optical systems and, as the demand for higher and higher angular resolution increases, the problem of surface finishing must be taken seriously even in optical telescopes. From the optical design of the instrument, reliable ray-tracing routines allow computing and display of the PSF based on geometrical optics. However, such an approach does not directly account for the scattering caused by surface microroughness, which is interferential in nature. Although the scattering effect can be separately modeled, its inclusion in the ray-tracing routine requires assumptions that are difficult to verify. In that context, a purely physical optics approach is more appropriate as it remains valid regardless of the shape and size of the defects appearing on the optical surface. Such a computation, when performed in two-dimensional consideration, is memory and time consuming because it requires one to process a surface map with a few micron resolution, and the situation becomes even more complicated in case of optical systems characterized by more than one reflection. Fortunately, the computation is significantly simplified in far-field configuration, since the computation involves only a sequence of Fourier Transforms. In this paper, we provide validation of the PSF simulation with Physical Optics approach through comparison with real PSF measurement data in the case of ASTRI-SST M1 hexagonal segments.
    [Show full text]
  • Modern Astronomical Optics 1
    Modern Astronomical Optics 1. Fundamental of Astronomical Imaging Systems OUTLINE: A few key fundamental concepts used in this course: Light detection: Photon noise Diffraction: Diffraction by an aperture, diffraction limit Spatial sampling Earth's atmosphere: every ground-based telescope's first optical element Effects for imaging (transmission, emission, distortion and scattering) and quick overview of impact on optical design of telescopes and instruments Geometrical optics: Pupil and focal plane, Lagrange invariant Astronomical measurements & important characteristics of astronomical imaging systems: Collecting area and throughput (sensitivity) flux units in astronomy Angular resolution Field of View (FOV) Time domain astronomy Spectral resolution Polarimetric measurement Astrometry Light detection: Photon noise Poisson noise Photon detection of a source of constant flux F. Mean # of photon in a unit dt = F dt. Probability to detect a photon in a unit of time is independent of when last photon was detected→ photon arrival times follows Poisson distribution Probability of detecting n photon given expected number of detection x (= F dt): f(n,x) = xne-x/(n!) x = mean value of f = variance of f Signal to noise ration (SNR) and measurement uncertainties SNR is a measure of how good a detection is, and can be converted into probability of detection, degree of confidence Signal = # of photon detected Noise (std deviation) = Poisson noise + additional instrumental noises (+ noise(s) due to unknown nature of object observed) Simplest case (often
    [Show full text]
  • Beat the Rayleigh Limit: OAM Based Super-Resolution Diffraction Tomography
    Beat the Rayleigh limit: OAM based super-resolution diffraction tomography Lianlin Li1 and Fang Li2 1Center of Advanced Electromagnetic Imaging, Department of Electronics, Peking University, Beijing 100871, China 2 Institute of Electronics, CAS, Beijing 100190, China This letter is the first to report that a super-resolution imaging beyond the Rayleigh limit can be achieved by using classical diffraction tomography (DT) extended with orbital angular momentum (OAM), termed as OAM based diffraction tomography (OAM-DT). It is well accepted that the orbital angular momentum (OAM) provides additional electromagnetic degrees of freedom. This concept has been widely applied in science and technology. In this letter we revisit the DT problem extended with OAM, demonstrate theoretically and numerically that there is no physical limits on imaging resolution in principle by the OAM-DT. This super-resolution OAM-DT imaging paradigm, has no requirement for evanescent fields, subtle focusing lens, complicated post- processing, etc., thus provides a new approach to realize the wavefield imaging of universal objects with sub-wavelength resolution. In 1879 Lord Rayleigh formulated a criterion that a conventional imaging system cannot achieve a resolution beyond that of the diffraction limit, i.e., the Rayleigh limit. Such a “physical barrier” characters the minimum separation of two adjacent objects that an imaging system can resolve. In the past decade numerous efforts have been made to achieve imaging resolution beyond that of Rayleigh limit. Among various proposals dedicated to surpass this “barrier”, a representative example is the well-known technique of near-field imaging, an essential sub-wavelength imaging technology. Near-field imaging relies on the fact that the evanescent component carries fine details of the electromagnetic field distribution at the immediate vicinity of probed objects [1].
    [Show full text]
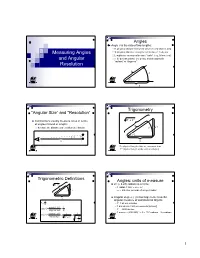
  • Measuring Angles and Angular Resolution
    Angles Angle θ is the ratio of two lengths: R: physical distance between observer and objects [km] Measuring Angles S: physical distance along the arc between 2 objects Lengths are measured in same “units” (e.g., kilometers) and Angular θ is “dimensionless” (no units), and measured in “radians” or “degrees” Resolution R S θ R Trigonometry “Angular Size” and “Resolution” 22 Astronomers usually measure sizes in terms R +Y of angles instead of lengths R because the distances are seldom well known S Y θ θ S R R S = physical length of the arc, measured in m Y = physical length of the vertical side [m] Trigonometric Definitions Angles: units of measure R22+Y 2π (≈ 6.28) radians in a circle R 1 radian = 360˚ ÷ 2π≈57 ˚ S Y ⇒≈206,265 seconds of arc per radian θ Angular degree (˚) is too large to be a useful R S angular measure of astronomical objects θ ≡ R 1º = 60 arc minutes opposite side Y 1 arc minute = 60 arc seconds [arcsec] tan[]θ ≡= adjacent side R 1º = 3600 arcsec -1 -6 opposite sideY 1 1 arcsec ≈ (206,265) ≈ 5 × 10 radians = 5 µradians sin[]θ ≡== hypotenuse RY22+ R 2 1+ Y 2 1 Number of Degrees per Radian Trigonometry in Astronomy Y 2π radians per circle θ S R 360° Usually R >> S (particularly in astronomy), so Y ≈ S 1 radian = ≈ 57.296° 2π SY Y 1 θ ≡≈≈ ≈ ≈ 57° 17'45" RR RY22+ R 2 1+ Y 2 θ ≈≈tan[θθ] sin[ ] Relationship of Trigonometric sin[θ ] ≈ tan[θ ] ≈ θ for θ ≈ 0 Functions for Small Angles 1 sin(πx) Check it! tan(πx) 0.5 18˚ = 18˚ × (2π radians per circle) ÷ (360˚ per πx circle) = 0.1π radians ≈ 0.314 radians 0 Calculated Results
    [Show full text]
  • Fundamentals of Astronomical Optical Interferometry
    Fundamentals of astronomical optical Interferometry OUTLINE: Why interferometry ? Angular resolution Connecting object brightness to observables -- Van Cittert-Zernike theorem Scientific motivations: – stellar interferometry: measuring stellar diameters – Exoplanets in near-IR and thermal IR Interferometric measurement – 2-telescope interferometer Interferometry and angular resolution Difraction limit of a telescope : λ/D (D: telescope diameter) Difraction limit of an interferometer: λ/B (B: baseline) Baseline B can be much larger than telescope diameter D: largest telescopes : D ~ 10m largest baselines (optical/near-IR interferometers): B ~ 100m - 500m Telescope vs. interferometer diffraction limit For circular aperture without obstruction : Airy pattern First dark ring is at ~1.22 λ/D Full width at half maximum ~ 1 λ/D The “Diffraction limit” term = 1 λ/D D=10m, λ=2 µm → λ/D = 0.040 arcsec This is the size of largest star With interferometer, D~400m → λ/B = 0.001 arcsec = 1 mas This is diameter of Sun at 10pc Many stars larger than 1mas History of Astronomical Interferometry • 1868 Fizeau first suggested stellar diameters could be measured interferometrically. • Michelson independently develops stellar interferometry. He uses it to measure the satellites of Jupiter (1891) and Betelgeuse (1921). • Further development not significant until the 1970s. Separated interferometers were developed as well as common-mount systems. • Currently there are approximately 7 small- aperture optical interferometers, and three large aperture interferometers (Keck, VLTI and LBT) 4 Interferometry Measurements wavefront Interferometers can be thought of in terms of the Young’s two slit setup. Light impinging on two apertures and subsequently imaged form an Airy disk of angular D width λ /D modulated by interference fringes of angular B frequency λ/B.
    [Show full text]
  • Overcoming the Diffraction-Limited Spatio-Angular Resolution Tradeoff
    Variable Aperture Light Field Photography: Overcoming the Diffraction-limited Spatio-angular Resolution Tradeoff Julie Chang1 Isaac Kauvar1 Xuemei Hu1,2 Gordon Wetzstein1 1Stanford University 2 Tsinghua University Abstract Small-f-number Large-f-number Light fields have many applications in machine vision, consumer photography, robotics, and microscopy. How- ever, the prevalent resolution limits of existing light field imaging systems hinder widespread adoption. In this pa- per, we analyze fundamental resolution limits of light field cameras in the diffraction limit. We propose a sequen- Depth-of-Field 10 tial, coded-aperture-style acquisition scheme that optimizes f/2 f/5.6 the resolution of a light field reconstructed from multiple f/22 photographs captured from different perspectives and f- 5 Blur-size-[mm] number settings. We also show that the proposed acquisi- 0 100 200 300 400 tion scheme facilitates high dynamic range light field imag- Distance-from-Camera-Lens-[mm] ing and demonstrate a proof-of-concept prototype system. Figure 1. Photographs captured with different f-number settings With this work, we hope to advance our understanding of exhibit different depths of field and also diffraction-limited resolu- the resolution limits of light field photography and develop tion for in-focus objects (top row). This effect is most pronounced practical computational imaging systems to overcome them. for macro photography, such as illustrated for a 50 mm lens fo- cused at 200 mm (bottom plot). Using multiple photographs cap- tured from different perspectives and with different f-number set- tings, the proposed method seeks to recover a light field with the 1.
    [Show full text]
  • Day Laboratory Exercise #3: Optics and Telescopes Page 1
    AS102 - Day Laboratory Exercise #3: Optics and Telescopes Page 1 DAY LABORATORY EXERCISE #3: OPTICS AND TELESCOPES Goals: To explore the functions of simple lenses To construct and use a refracting telescope To understand the concepts of focal length, focal ratio, and magnification. To study aberrations in simple telescope systems. To explore the concept of angular resolution. Equipment: Lens kits, optical benches, light sources, rulers, calculators Methods: Measure lens focal lengths by forming images of distant objects Focus refracting telescope on distant object - measure lens separations Compare optical aberrations of refracting and reflecting telescopes Explore optical systems using a multiple lens optics kit and light source Measure angular resolution of the eye using distant eye chart Introduction - Telescopes are the primary instruments for the acquisition of data by astronomers. This exercise investigates the basic principles of geometric optics as applied to telescopes. You will primarily use refracting telescopes for the examples, but what you learn can be applied to any telescope (i.e., reflecting or radio). Lenses and Mirrors - A positive lens has at least one convex surface and is capable of focusing light from a distant object into a real image, that is, an image which can be seen projected onto a screen (see Figure 1). However, the same lens, when placed close to an object, produces a magnified virtual image which can be seen through the lens with the eye, but cannot be projected onto a screen (see Figure 2). A negative lens has at least one concave surface and always produces a virtual image. All of the lenses in this exercise have convex surfaces (the glass surface bulges outward from the lens center).
    [Show full text]
  • Title: the Future of Photography Is Computational Photography
    Title: The Future of Photography is Computational Photography Subtitle: 100 years after invention, Integral Photography becomes feasible Adobe customers are creative and demanding. They expect to use our Adobe Photoshop software to create the “impossible photograph.” They want what they imagined, not the image that the camera captured. To help them close the gap between the image and their imaginations, we are constantly researching and designing new approaches. The computational power available to Adobe Photoshop has grown exponentially, thanks to Moore’s Law. We at Adobe find that we now have algorithms for image manipulation and enhancement that cannot be applied commercially without advances in the camera as well. This fact has led us to innovate not only in software, but also in hardware, and we’ve begun prototyping the kind of computational cameras and lenses we would like to see produced in order to enable these new algorithms. The integral (or plenoptic) camera is a promising advancement in this work. In this article, we will outline our motivations and inspirations for this research. We will show how our work builds on that of other scientists, especially Gabriel Lippmann, winner of the Nobel Prize for color photography. We will discuss his idea of the “integral photograph” (Lippmann 1908) and how current research manifests this idea. We also will describe the applications of this novel approach, and demonstrate some of the results of our research on the merging of photography and computation. Perhaps we may even inspire you to contribute in some way to the future of photography, which we believe is computational photography.
    [Show full text]