The Impact of Objective and Subjective Measures of Air Quality and Noise on House Prices: a Multilevel Approach for Downtown Madrid
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

00 Pag I a IV.Indd
LA GEOGRAFÍA DEL TALENTO EN LA CIUDAD DE MADRID Rubén GARRIDO YSERTE María Teresa GALLO RIVERA Universidad de Alcalá Resumen Abstract Algunos núcleos urbanos se han convertido a lo largo de los años Some urban centers have become, over the years, worldwide en referencias mundiales en la gestión y la retención del talento. Es el references in the attraction and retention of talent. This is the case of caso de la ciudad de Madrid, como así lo destaca el último Índice de the city of Madrid, as the latest Competitiveness Index for Global Talent Competitividad por el Talento Global (GTCI). En este trabajo se analiza (GTCI) highlights. This paper analyzes the geographical distribution la distribución geográfica y las dinámicas espaciales de los trabajadores and spatial dynamics of creative class workers in the city of Madrid. de la clase creativa en la ciudad de Madrid. Se presentan los resulta- The results of Index of Creativity by Districts (ICD) and neighborhoods dos de los Índices de Creatividad por Distritos (ICD) y por Barrios (ICB) (ICB) are showed with the aim of analyze the factors that foster the con el objeto de analizar los factores que impulsan la competitividad competitiveness of talent in the city of Madrid. del talento en la ciudad de Madrid. Key words: Talent, creative industries, spatial concentration, Palabras clave: Talento, industrias creativas, concentración espacial, neighborhoods, districts, Madrid. barrios, distritos, Madrid. JEL classification: J24, O18, O30, R23. Los conceptos de talento y creatividad han ido I. INTRODUCCIÓN evolucionando en los últimos quince años. Aunque no han estado exentos de críticas por la comple- A preocupación de los decisores políticos por jidad que encierran y por considerarse conceptos impulsar la capacidad de las ciudades para todavía difusos, difíciles de hacer operativos, y que Latraer a trabajadores talentosos o de la clase han polarizado el debate sobre sus efectos sobre el creativa se sustenta en varios motivos. -

Plano De Los Transportes Del Distrito De Usera
AEROPUERTO T4 C-1 CHAMARTÍN C-2 EL ESCORIAL C-3 ALCOBENDAS-SAN. SEB. REYES/COLMENAR VIEJO C-4 PRÍNCIPE PÍO C-7 FUENTE DE LA MORAN801 C-7 VILLALBA-EL ESCORIAL/CERCEDILLAN805 C-8 VILLALBA C-10 Plano de los transportes delN806 distrito de Usera Corrala Calle Julián COLONIA ATOCHA 36 41 C1 3 5 ALAMEDA DE OSUNA Calle Ribera M1 SEVILLA MONCLOA M1 SEVILLA 351 352 353 AVDA. FELIPE II 152 C1 CIRCULAR PAVONES 32 PZA. MANUEL 143 CIRCULAR 138 PZA. ESPAÑA ÓPERA 25 MANZANARES 60 60 3 36 41 E1 PINAR DE 1 6 336 148 C Centro de Arte C s C 19 PZA. DE CATALUÑA BECERRA 50 C-1 PRÍNCIPE PÍO 18 DIEGO DE LEÓN 56 156 Calle PTA. DEL SOL . Embajadores e 27 CHAMARTÍN C2 CIRCULAR 35 n Reina Sofía J 331 N301 N302 138 a a A D B E o G H I Athos 62 i C1 N401 32 Centro CIRCULAR N16 l is l l t l F 119 o v 337 l PRÍNCIPE PÍO 62 N26 14 o C-7 C2 S e 32 Conde e o PRÍNCIPE PÍO P e Atocha Renfe C2 t 17 l r 63 K 32 a C F d E P PMesón de v 59 N9 Calle Cobos de Segovia C2 Comercial eña de CIRCULAR d e 23 a Calle 351 352 353 n r lv 50 r r EMBAJADORES Calle 138 ALUCHE ú i Jardín Avenida del Mediterráneo 6 333 332 N9 p M ancia e e e N402 de Casal 334 S a COLONIA 5 C1 32 a C-10 VILLALBA Puerta M1 1 Paseo e lle S V 26 tin 339 all M1 a ris Plaza S C Tropical C. -

Distrito Carabanchel
Bellas Vistas Elaborado por el Servicio de Convivencia Intercultural en Barrios 19/06/2015 Contenido A. CARACTERISTICAS GENERALES DEL DISTRITO. ..................... ¡Error! Marcador no definido. 1. Descripción Espacial del Distrito. ......................................... ¡Error! Marcador no definido. 2. Historia del Distrito. ............................................................................................................ 4 3. Análisis Socio-Demográfico. ................................................. ¡Error! Marcador no definido. 4. Economía del Distrito ........................................................... ¡Error! Marcador no definido. 5. Datos Comparativos sobre Empleo y Desempleo ................ ¡Error! Marcador no definido. 6. Educación, Cultura y Deporte .............................................. ¡Error! Marcador no definido. 7. Infancia y Adolescencia ........................................................ ¡Error! Marcador no definido. 8. Salud Comunitaria ……………………………………………………………………………………………………….24 9. Historia Administrativo y Participación Política …………………………………………………………..25 B. CARACTERÍSTICAS GENERALES DEL BARRIO BELLAS VISTAS ............................................ 31 1. Delimitación espacial: barrio administrativo, barrio sentido. .......................................... 31 2. Historia del barrio.............................................................................................................. 33 3. Análisis socio-demográfico .................................................. -

Inmate Release Report Snapshot Taken: 9/28/2021 6:00:10 AM
Inmate Release Report Snapshot taken: 9/28/2021 6:00:10 AM Projected Release Date Booking No Last Name First Name 9/29/2021 6090989 ALMEDA JONATHAN 9/29/2021 6249749 CAMACHO VICTOR 9/29/2021 6224278 HARTE GREGORY 9/29/2021 6251673 PILOTIN MANUEL 9/29/2021 6185574 PURYEAR KORY 9/29/2021 6142736 REYES GERARDO 9/30/2021 5880910 ADAMS YOLANDA 9/30/2021 6250719 AREVALO JOSE 9/30/2021 6226836 CALDERON ISAIAH 9/30/2021 6059780 ESTRADA CHRISTOPHER 9/30/2021 6128887 GONZALEZ JUAN 9/30/2021 6086264 OROZCO FRANCISCO 9/30/2021 6243426 TOBIAS BENJAMIN 10/1/2021 6211938 ALAS CHRISTOPHER 10/1/2021 6085586 ALVARADO BRYANT 10/1/2021 6164249 CASTILLO LUIS 10/1/2021 6254189 CASTRO JAYCEE 10/1/2021 6221163 CUBIAS ERICK 10/1/2021 6245513 MYERS ALBERT 10/1/2021 6084670 ORTIZ MATTHEW 10/1/2021 6085145 SANCHEZ ARAFAT 10/1/2021 6241199 SANCHEZ JORGE 10/1/2021 6085431 TORRES MANLIO 10/2/2021 6250453 ALVAREZ JOHNNY 10/2/2021 6241709 ESTRADA JOSE 10/2/2021 6242141 HUFF ADAM 10/2/2021 6254134 MEJIA GERSON 10/2/2021 6242125 ROBLES GUSTAVO 10/2/2021 6250718 RODRIGUEZ RAFAEL 10/2/2021 6225488 SANCHEZ NARCISO 10/2/2021 6248409 SOLIS PAUL 10/2/2021 6218628 VALDEZ EDDIE 10/2/2021 6159119 VERNON JIMMY 10/3/2021 6212939 ADAMS LANCE 10/3/2021 6239546 BELL JACKSON 10/3/2021 6222552 BRIDGES DAVID 10/3/2021 6245307 CERVANTES FRANCISCO 10/3/2021 6252321 FARAMAZOV ARTUR 10/3/2021 6251594 GOLDEN DAMON 10/3/2021 6242465 GOSSETT KAMERA 10/3/2021 6237998 MOLINA ANTONIO 10/3/2021 6028640 MORALES CHRISTOPHER 10/3/2021 6088136 ROBINSON MARK 10/3/2021 6033818 ROJO CHRISTOPHER 10/3/2021 -

Curriculum Vitae Susana Aurora Magallón Puebla
1 CURRICULUM VITAE SUSANA AURORA MAGALLÓN PUEBLA Instituto de Biología Universidad Nacional Autónoma de México ORCID ID: https://orcid.org/0000-0002-6838-7497 1. DATOS PERSONALES • Nacionalidad: Mexicana. • Hijos: una hija, n. 3 de Junio de 2004. 2. CONTACTO • Departamento de Botánica, Instituto de Biología, Universidad Nacional Autónoma de México; 3er Circuito de Ciudad Universitaria; Del. Coyoacán, México D.F. 04510, México. Teléfono: (52- 55) 5622-9087. • E-mail: [email protected]. • http://www.ib.unam.mx/directorio/101 • https://www.researchgate.net/profile/Susana_Magallon 3. DATOS LABORALES 3a. Nombramiento Actual • Investigador Titular C de Tiempo Completo, Departamento de Botánica, Instituto de Biología, UNAM. Agosto, 2017. • Definitividad en la UNAM: 30 de Septiembre de 2005. 3b. Experiencia Laboral • Ayudante de Profesor B, Museo de Paleontología, Facultad de Ciencias, UNAM. 1987-1994. • Ayudante de Profesor B, Botánica III, Licenciatura en Biología, UNAM. 1989-1991. • Research Assistant. Geology Department, Field Museum of Natural History, Chicago, IL, USA. 1998-1999 • Visiting Research Scientist. University of California, Davis, USA. 1999-2001 • Investigador Titular A de Tiempo Completo, Instituto de Biología, UNAM. 2001-2007 • Investigador Titualr B de Tiempo Completo, Instituto de Biología, UNAM. 2007-2017. • Visiting Professor. Departmento of Botany and Centre for Biodiversity Research, University of British Columbia, Vancouver, Canada. 2017-2018. 4. ESTÍMULOS A LA PRODUCTIVIDAD 4a. Programa de Primas al Desempeño del Personal Académico de Tiempo Completo (PRIDE) Susana Magallón Puebla Curriculum Vitae Mayo, 2019 2 • Nivel C. 2003-2005 • Nivel D. 2006-2010 • Nivel D. 2011-2015 • Nivel D. 2016-2020 4b. Sistema Nacional de Investigadores • Beca equivalente a Investigador Nacional nivel I, asignado como parte del programa de repatriación del CONACyT. -
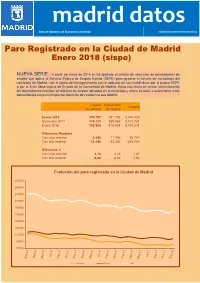
Enero 2018 (Sispe)
Área de Gobierno de Economía y Hacienda Subdirección General de Estadística Paro Registrado en la Ciudad de Madrid Enero 2018 (sispe) NUEVA SERIE: A partir de enero de 2014 se ha ajustado el criterio de selección de demandantes de empleo que aplica el Servicio Público de Empleo Estatal (SEPE) para generar el fichero de microdatos del municipio de Madrid, con el objeto de homogeneizarlo con el aplicado en sus estadísticas por el propio SEPE o por el Área Observatorio de Empleo de la Comunidad de Madrid. Hasta esa fecha se venían seleccionando los demandantes inscritos en oficinas de empleo ubicadas en el municipio y ahora se pasa a seleccionar a los demandantes cuyo municipio del domicilio de residencia sea Madrid. Ciudad Comunidad España de Madrid de Madrid Enero 2018 179.757 381.732 3.476.528 Diciembre 2017 174.212 369.966 3.412.781 Enero 2016 192.905 415.034 3.760.231 Diferencia Absoluta Con mes anterior 5.545 11.766 63.747 Con año anterior -13.148 -33.302 -283.703 Diferencia % NOTA:Con En cursivames anterior datos estimados 3,18 3,18 1,87 Con año anterior -6,82 -8,02 -7,54 Evolución del paro registrado en la Ciudad de Madrid 270000 250000 230000 210000 190000 170000 150000 130000 110000 90000 70000 Hombres Mujeres Total 0. Paro registrado por sexo y mes Parados Índice de Mes TotalHombres Mujeres feminización 60 y más 55 - 59 2017 Enero 192.905 89.761 103.144 114,9 50 - 54 Febrero 194.232 90.030 104.202 115,7 45 - 49 Marzo 191.437 88.336 103.101 116,7 Abril 186.033 85.357 100.676 117,9 40 - 44 Mayo 181.735 82.796 98.939 119,5 Junio 179.324 80.059 99.265 124,0 35 - 39 Julio 180.274 79.345 100.929 127,2 30 - 34 Agosto 182.379 80.106 102.273 127,7 Septiembre 181.859 80.458 101.401 126,0 25 - 29 Octubre 181.715 80.900 100.815 124,6 20 - 24 Noviembre 178.399 79.515 98.884 124,4 Diciembre 174.212 78.544 95.668 121,8 16 - 19 20.000 15.000 10.000 5.000 0 5.000 10.000 15.000 20.000 2018 Mujeres Hombres Enero 179.757 81.320 98.437 121,0 Paro por sexo y edad Fuente: SEPE. -

Anexo 10 Equipos De Orientación Educativa Y Psicopedagógica, Generales, Específicos Y De Atención Temprana
Anexo 10 Equipos de Orientación Educativa y Psicopedagógica, Generales, Específicos y de Atención Temprana CLAVE DE IDENTIFICACIÓN DE LAS SIGLAS UTILIZADAS: GENERA: GENERALES; ESPECI: ESPECÍFICAS; ATENT-T: ATENCIÓN TEMPRANA ORDENACIÓN REALIZADA: 1: DIRECCIÓN DE ÁREA 2: LOCALIDAD 3: DISTRITO 4: BARRIO 5: CÓDIGO POSTAL 6: CÓDIGO DE CENTRO DIRECCIÓN DE ÁREA: MADRID-CAPITAL COD.C. TIPO NOMBRE DOMICILIO COD.LOC LOCALIDAD COD.DIST. DISTRITO BARRIO MUNICIPIO CP ZONA CON. 28700532 ATENT-T Equipo Atencion Calle Del Mar Caspio 6 280790001 Madrid 280791601 Hortaleza Madrid 28033 280010 Temprana Hortaleza 28700544 ATENT-T E. A. Temprana Calle De Tembleque 58 1º 280790001 Madrid 280791001 Latina Aluche Madrid 28024 280010 Latina-Carabanchel- Centro 28700581 ATENT-T E. A. Temprana Calle Del Pico De Los Artilleros 280790001 Madrid 280791301 Puente de Palomeras Sureste Madrid 28030 280010 Moratalaz-Villa 123 Vallecas Vallecas 28700556 ATENT-T Equipo Atencion Calle De Luis Marín 1 280790001 Madrid 280791301 Puente de Palomeras Sureste Madrid 28038 280010 Temprana Puente Vallecas Vallecas 28700568 ATENT-T Equipo Atencion Avda Canillejas A Vicalvaro 82 280790001 Madrid 280792001 San Blas Arcos Madrid 28022 280010 Temprana San Blas 28700738 ESPECI Deficiencias Visuales Avda De Canillejas A Vicálvaro 280790001 Madrid 280792001 San Blas Arcos Madrid 28022 280010 82 28700571 ATENT-T Equipo Atencion Calle De Las Magnolias 82 280790001 Madrid 280790601 Tetuán Almenara Madrid 28029 280010 Temprana Tetuan 28700593 ATENT-T Equipo Atencion Calle Del Consenso 10 280790001 Madrid 280791201 Usera Orcasur Madrid 28041 280010 Temprana Villaverde DIRECCIÓN DE ÁREA: MADRID-ESTE COD.C. TIPO NOMBRE DOMICILIO COD.LOC LOCALIDAD COD.DIST. DISTRITO BARRIO MUNICIPIO CP ZONA CON. -

“Diagnóstico De Convivencia Vecinal E Intercultural” Distrito De Tetuán
“Diagnóstico de Convivencia vecinal e intercultural” Distrito de Tetuán COMISIÓN DE ESTUDIOS MESA CONTRA LA EXCLUSIÓN Y POR LOS DERECHOS SOCIALES 1 El Objetivo del presente diagnóstico de la Comisión de Estudios de la Mesa contra la Exclusión y por los Derechos sociales(1) es realizar una evaluación de la situación actual de la Convivencia vecinal e intercultural en el distrito de Tetuán, incidiendo especialmente en las situaciones de exclusión social existentes en el mismo. Relaciones de Convivencia-Coexistencia-Conflicto. Entendemos por “convivencia” las formas de relación (cómo nos tratamos/nos vemos) existentes entre los diversos habitantes del distrito en el contexto social actual. Para afrontar este estudio de las relaciones interpersonales adoptamos la clasificación de los modos de sociabilidad propuesta por Carlos Giménez (2005), según la cual existe un continuum entre las relaciones de convivencia (respeto a la diversidad, confianza y comunicación), coexistencia (relaciones pacíficas pero distantes, sin interés por lo diverso, poca comunicación y evitación del conflicto) y conflicto u hostilidad (incomunicación, confrontación, desconfianza e interés en excluir al otro). Nuestro Foco de interés son las personas y colectivos en situación de exclusión o emergencia social (cómo son tratados/percibidos desde fuera; cómo se sitúan/ven las cosas ellos mismos). A lo largo de este Diagnóstico nos proponemos analizar como inciden una serie de factores determinantes de la exclusión en las relaciones de convivencia. El diagnóstico intenta abordar las causas estructurales que están en la base de los problemas de convivencia en el espacio público (desigualdad social, violencia estructural, paro y precariedad laboral, problemas de vivienda, alimentación, pobreza energética…) Metodología. -

Changes in the Social Composition of the Neighborhoods of Barcelona and Madrid: an Approach Using Migration and Residential Flows
Changes in the Social Composition of the Neighborhoods of Barcelona and Madrid: An Approach Using Migration and Residential Flows LÓPEZ GAY, Antonio Centre d’Estudis Demogràfics [email protected] ANDÚJAR LLOSA, Andrea Universidad Pablo de Olavide [email protected] THIS IS A PRELIMINAR VERSION PREPARED FOR THE POPULATION ASSOCIATION OF AMERICA CONFERENCE 2019 Abstract Numerous neighborhoods in Barcelona and Madrid are currently undergoing intense transformation of their social composition. Exclusive (and excluding) areas have seemed to expand within the context of the resurgence of central spaces. The literature suggests that in parallel with this expansion, the most vulnerable population is being displaced and concentrated in suburban areas with worse access to all types of services. These changing processes in social composition at the intraurban scale cannot be understood without underlining the key role of migration and residential mobility. This article analyzes annual data on migration and residential mobility based on the population register of both cities. For the first time in the country, we have been able to include the variable level of studies to the dataset, which allows us to dissect the processes of substitution, polarization and segregation of the population. Keyword: Residential mobility, skilled migration, displacement, gentrification, suburbanization of poverty Introduction The neighborhoods of Barcelona and Madrid are undergoing intense transformations of their social composition due to a genuine struggle by residents to reside in certain areas of the city. In many neighborhoods, housing market prices, especially those of rental properties, exceed the prices reached at the end of the last expansive stage of the Spanish property market and have markedly increased since 2015. -

06. Tetuán 77 a 84 Padrón Mucnicipal 2
Distrito 06 - Tetuán Ü 085 064 065 066 063 061 062 Barrios 61 - Bellas Vistas 62 - Cuatro Caminos 63 - Castillejos 64 - Almenara 65 - Valdeacederas 66 - Berruguete Dirección General de Estadística Tetuán Explotación del Padrón Municipal de Habitantes 2014 1a. Evolución de la población Población a 1 de enero 2004 2005 2006 2007 2008 2009 2010 2011 2012 2013 2014 6. Tetuán 150.834 150.379 152.615 152.206 154.470 156.658 157.527 156.433 155.764 155.684 152.523 6.1. Bellas Vistas 29.347 28.769 28.953 28.836 29.567 29.886 29.801 29.590 29.262 29.074 28.326 6.2. Cuatro Caminos 35.981 36.130 36.412 34.900 34.883 34.846 34.693 34.473 34.244 34.252 33.633 6.3. Castillejos 20.688 20.904 20.893 20.519 20.619 20.787 20.705 20.502 20.343 20.397 19.963 6.4. Almenara 18.807 18.414 19.759 20.899 21.470 21.920 22.359 22.137 22.179 22.110 21.897 6.5. Valdeacederas 23.215 23.373 23.606 23.937 24.409 24.995 25.270 25.231 25.286 25.494 24.921 6.6. Berruguete 22.796 22.789 22.992 23.115 23.522 24.224 24.699 24.500 24.450 24.357 23.783 Ciudad de Madrid 3.162.304 3.167.424 3.205.334 3.187.062 3.238.208 3.273.006 3.284.110 3.269.861 3.237.937 3.215.633 3.166.130 1b. -

Imaginación Y Literatura En La Enseñanza Del Español, A
IMAGINACIÓN Y LITERATURA EN LA ENSEÑANZA DEL ESPAÑOL, A TRAVÉS DE DOS TEXTOS DE DULCE MARÍA LOYNAZ Coralina Ramírez-Brothers Submitted to the faculty of the University Graduate School in partial fulfillment of the requirements for the degree Master of Arts in the Teaching of Spanish in the Department of World Languages and Cultures, Indiana University December 2010 Accepted by the Faculty of Indiana University, in partial fulfillment of the requirements for the degree of Master of Arts in the Teaching of Spanish. ___________________________ Rosa Tezanos-Pinto, Ph.D., Chair ___________________________ Nancy A. Newton, Ph.D. Master’s Thesis Committee ___________________________ J. Agustín Torijano, Ph.D. ii DEDICATORIA En todos mis trabajos están presentes la devoción, el amor y el agradecimiento a mis padres, Reinaldo Ramírez Rosell y Milagros Fuentes; el amor a mis hermanos, Nando y Alex; a Alejandrito, Sabrina, Daniel y Sarah Grace; y el amor a mi esposo y eterno compañero, Timothy Steven Brothers. iii AGRADECIMIENTOS A la Virgen María por su constante luz y protección. A la presencia espiritual de Dulce María Loynaz. A todas las personas que me brindaron generosamente su talento y su tiempo: Tim, con sus sugerencias vitales desde el inicio del proyecto y con su compañía a lo largo de él; Nancy Newton, quien me dio libertad para seleccionar el tema; Agustín Torijano, por la paciencia en la querida España; Rosa Tezanos-Pinto, tutora y apoyo imprescindible en este trabajo. A mi hermano Alex y a su esposa Janet, quienes me albergaron en su casa tres días intensos hasta la finalización del escrito. -

1 Nombre De La Experiencia HUERTO COMUNITARIO DE ADELFAS Y
Nombre de la Experiencia HUERTO COMUNITARIO DE ADELFAS Y RED DE HUERTOS MADRID Lugar España, Comunidad de Madrid, Madrid. Resumen Desde hace tres años existe en Madrid una realidad emergente respecto a la agricultura urbana, especialmente en su vertiente de construcción de huertos comunitarios recuperando espacios degradados o en desuso. Impulsadas por el movimiento vecinal y ecologista los huertos urbanos están dando pie a experiencias de participación ciudadana de nuevo cuño. Dinámicas que parecen haberse consolidado en la realidad urbana, generando espacios de encuentro y coordinación, procesos formativos, así como canales de diálogo con la administración local. Este trabajo reflexiona sobre los aportes en favor de la soberanía alimentaria que se vienen realizando desde los contextos urbanos, y de forma especial desde los huertos comunitarios. El texto desarrolla la multidimensionalidad de estas iniciativas, centrándose especialmente en sus aspectos sobre la sostenibilidad urbana y la cohesión social. La sistematización realizada se focaliza en una experiencia concreta, el Huerto Comunitario de Adelfas, así como en la Red Huertos Urbanos de Madrid, de forma que nos permita una comprensión del fenómeno a una escala mayor. Palabras clave Producción y consumo; agricultura urbana; urbanos, proyectos de autogestión/comunitarios; movimiento vecinal, ecología urbana, urbanismo sostenible. Persona(s) sistematizadora(s) José Luis Fernández Casadevante KOIS Fecha: Mayo de 2011/Diciembre 2011 Nombre de la ExperienciaSistematización de experiencias en Soberanía alimentaria y Agroecología 1 PRIMERA PARTE A.- DESCRIPTORES GENERALES: 1. Nombre de la experiencia: HUERTO COMUNITARIO DE ADELFAS Y RED DE HUERTOS MADRID 2. Lugar (País, Región, Municipio): España, Comunidad de Madrid, Madrid. 3. Contexto geográfico: Una metrópolis de más de 5 millones de habitantes con un intenso crecimiento urbano, que casi ha colmatado el suelo existente en el término municipal.